Sparse linear discriminant analysis via ℓ0 constraint
Qi Yin,and Lei Shu
Department of Statistics and Finance,School of Management,University of Science and Technology of China,Hefei 230026,China
Abstract: We consider the problem of interpretable classification in a high-dimensional setting,where the number of features is extremely large and the number of observations is limited.This setting has been extensively studied in the chemometric literature and has recently become pervasive in the biological and medical literature.Linear discriminant analysis(LDA) is a canonical approach for solving this problem.However,in the case of high dimensions,LDA is unsuitable for two reasons.First,the standard estimate of the within-class covariance matrix is singular;therefore,the usual discriminant rule cannot be applied.Second,when p is large,it is difficult to interpret the classification rules obtained from LDA because p features are involved.In this setting,motivated by the success of the primal-dual active set algorithm for best subset selection,we propose a method for sparse linear discriminant analysis via ℓ0 constraint,which imposes a sparsity criterion when performing linear discriminant analysis,allowing classification and feature selection to be performed simultaneously.Numerical results on synthetic and real data suggest that our method obtains competitive results compared with existing alternative methods.
Keywords: best subset selection;linear discriminant analysis;ℓ0 constraint;projection
1 Introduction
Linear discriminant analysis (LDA) is a prevalent supervised classification tool in many applications,owing to its simplicity,robustness,and predictive accuracy.LDA uses label information to learn discriminant projections,which can dramatically maximize the between-class distance and decrease the within-class distance,thus improving classification accuracy. Simultaneously,low-dimensional data projections in most discriminant directions are valuable for data interpretation.LDA classifiers can be constructed in three different ways: the multivariate Gaussian model,optimal scoring problem,and Fisher’s discriminant problem (see,for example,Hastie et al.[1]).
LDA is effective and asymptotically optimal when the dimensionpis fixed and the number of observationsnis large;that is,its misclassification rate converges to 0 over the optimal rule asnincreases to infinity.Shao et al.[2]indicated that LDA remainps asymptotic when diverges to infinity at a rate slower thanHowever,with tremendous advances in data collection,high-dimensional data with dimensionppotentially larger than the number of observationsnare now frequently encountered in a wide range of applications,and the classification of these data has recently attracted considerable attention.Common applications include genomics,functional magnetic resonance imaging,risk management,and web searches.
In high-dimensional settings,standard LDA performs poorly and may even fail completely.For example,Bickel and Levina[3]indicated that LDA could not perform better than random guessing whenp>n.In addition,in this case,the sample covariance matrix is singular,and its inverse matrix is not well identified.Consequently,it is challenging to select and extract the most discriminative features for supervised classification.A natural solution is to replace the inverse matrix with the generalized inverse matrix of the sample covariance matrix.However,such an estimation is highly biased,unrobust,and can contribute to the poor performance of the classifier.Whenpis large,the resulting classifier is difficult to interpret because the classification rules involve a linear combination of allpfeatures.Thus,whenp≫n,one may desire a classifier with parsimonious features,that is,a classifier that involves only a subset ofpfeatures.Such a sparse classifier ensures that the model is easier to interpret and can reduce the overfitting of training data.
Recently,several studies have extended LDA to highdimensional settings.Some of this literature addressed nonsparse classifiers.For example,in multivariate Gaussian models of LDA,Dudoit et al.[4]and Bickel and Levina[3]assumed the independence of features (naive Bayes) and Friedman[5]suggested applying a ridge penalty to the within-class covariance matrix.Xu et al.[6]considered other positive definite estimates of the within-class covariance matrix.In addition,some research on sparse classifiers has been conducted.Tibshirani et al.[7]adapted a naive Bayesian classifier by soft thresholding the mean vector,and Guo et al.[8]combined a ridge-type penalty on the within-class covariance matrix with a soft thresholding operation.Witten and Tibshirani[9]employed an ℓ1penalty for Fisher’s discriminant problem to obtain sparse discriminant vectors,but this approach does not generalize to the Gaussian mixture setting and lacks simplicity if it is in regression-based optimal scoring problems.
Motivated by the Fisher’s discriminant framework of Witten and Tibshirani[9],we develop a sparse version of LDA with the ℓ0constraint.Previous sparse LDAs were typically implemented by imposing penalties of ℓ1,ℓ2,or a mixture of ℓ1and ℓ2,because ℓ0regularization is non-convex and NP-hard.Whether the optimization problem is more correct is based on the prediction effectiveness,false discovery rate,and sparsity interpretation. ℓ0penalized methods have lower error bounds than ℓ1methods.Mathematically,for a pre-specified degree of sparsitys,the discriminant vector can be determined by the following optimization problem:

where ∥β∥0denotes the number of nonzero elements of β ,Σbis the between-class covariance matrix,and Σwis the withinclass covariance matrix. Further details are introduced in Section 2.
This study presents a new iterative thresholding algorithm to estimate linear discriminant vectors,which is a development of the primal-dual active-set algorithm proposed by Zhu et al.[10]to solve the best subset selection problem in regression.The contribution of this study is two-fold.First,we consider addressing the estimation problem of sparse LDA by directly solving the ℓ0constrained optimization problem,which avoids unnecessary information loss owing to relaxing the constraints. Second,we constructed a polynomial algorithm for estimating sparse linear discriminant vectors,which is computationally efficient and easy to implement.
The remainder of this paper is organized as follows.In Section 2,we review LDA and classical solution procedures and then propose a new solution for sparse linear discriminant analysis.Sections 3 and 4 compare the results of our proposed method and existing methods in simulated experiments and applications to real data,respectively.Section 5 presents our conclusions.
2 Methodology
2.1 A review of linear discriminant analysis
LetXbe ann×pdata matrix withpfeatures measured onnobservations and suppose that each of thenobservations belongs to one of theKclasses.In addition,we assume that each of thepfeatures is centered to satisfy the zero mean and is normalized to have an identical variance if they are not measured on the same scale.Letxidenote theith observation and Ckdenote the index set of observations in thekth class.


Because the rank of Σbis at mostK−1,the above-generalized eigenproblem has at mostK−1 nontrivial solutions and,therefore,at mostK−1 discriminant vectors.These solutions are the directions in which the data have the maximal betweenclass covariance relative to their within-class covariance.Moreover,it has been demonstrated that classification based on the nearest centroid of matrix (Xβ1,···,XβK−1) produces the same LDA classification rule as the multivariate Gaussian model described previously (see Hastie et al.[1]).One advantage of Fisher’s discriminant problem over the multivariate Gaussian model of LDA is that it allows for reduced-rank classification by performing nearest centroid classification on the matrix (Xβ1,···,Xβq) withq The standard estimate of the within-class covariance matrix Σwis: wherenk=|Ck|. In later subsections,we will make use of the fact that whereYis ann×Kmatrix andYikis an indicator of whether observationiis in thekth class.Then,the empirical version of LDA can be written as The new optimization problem (3) addresses the singularity issue but not the interpretability issue.At this point,we extend problem (3) such that the resulting discriminant vector is interpretable.We use Lemma 2.1,which provides a reformulation of problem (3) to obtain the same solution. Lemma 2.1.The solutionto problem (3) is equivalent to the solution to the following problem: Recall that the Lagrangian form of (4) is as follows: Owing to the discontinuity of the ℓ0norm,the naive algorithm for sparse linear discriminant analysis may converge to a local minimum and encounter the problem of periodic iterations.To obtain sparse linear discriminant vectors more efficiently,an iterative algorithm based on the primal-dual condition of problem (5) was proposed in this subsection.Motivated by Zhu et al.[10],who developed a novel algorithm based on exchanging active sets to avoid periodic iterations in solving the best subset selection problem in linear regression models,we extended their work to the sparse LDA problem.An exchanging step is added to Algorithm 2.1 to prevent the algorithm from entering a loop,that is,choosing a subset of the active set to exchange with a subset of the inactive set.We then decide whether to adopt the new candidate solution by comparing the objective function values before and after the exchange. Specifically,at themth iteration of computing thekth discriminant vector of Algorithm 2.1,we obtain the sacrifice(m).Subsequently,we classified the variables that needed to be exchanged in the active and inactive sets. ● Subset of the active set that need to be exchanged to the inactive set: ● Subset of the inactive set that need to be exchanged to the active set: process of exchanging some variables in the active and inactive sets. Based on the exchange step proposed above,we developed an efficient algorithm to avoid falling into a local minimum and guarantee convergence.Specifically,we added an exchange step after updating the primal and dual variables in Algorithm 2.1.The details are presented in Algorithm 2.3,which is called SLDA-BESS. The improved Algorithm 2.3 has the theoretical guarantee of Theorem 2.1,which indicates that such a best subset selection algorithm incorporating the exchange step is feasible. Theorem 2.1.The SLDA-BESS algorithm terminates after a finite number of iterations. Proof.The objective function always increases,and the choice of the active set is finite.Algorithm 2.3 terminates after a finite number of iterations. We compared SLDA-BESS with penalized LDA-ℓ1[9],nearest shrunken centroids (NSC)[7],and shrunken centroids regularized discriminant analysis (RDA)[8]in simulation studies.LDA-ℓ1is a method that adds a ℓ1penalty to the objective function β⊤Σβ.NSC is a simple modified version of the nearest centroid method that divides a between-class standard deviation when calculating the centroid distance and is a modified version based on NSC.In each simulation,1 200 observations were set to belong equally to several different classes.Arbitrary 300 of these 1200 observations are set as the training set,and the remaining 900 belong to the test set.Each simulation consisted of measurements of 500 features,i.e.,p=500. Simulation 1.Consider four different classes where the features are independent of each other and the mean value is shifted.Given the set of indicators for four classes,C1,C2,C3andC4,xi∼N(µk,I) ifi∈Ck,where µ1,j=0.7 for 1 ≤j≤25,µ2,j=0.7 for 26 ≤j≤50,µ3,j=0.7 for 51 ≤j≤75,µ4,j=0.7 for 7 6 ≤j≤100 and µk j=0 otherwise forj=1,...,500. Simulation 2.Consider two different classes where the features are dependent of each other and the mean value is shifted.Given the set of indicators for two classes,C1andC2,xi∼N(0,Σ) fori∈C1andxi∼N(µ,Σ) fori∈C2,whereµj=0.6 ifj≤100 and µj=0 otherwise and Σ=(Σij)=(0.6|i−j|). The covariance structure Σ is intended to mimic gene expression data,in which genes are positively correlated within a pathway and independent between pathways. Simulation 3.Consider four different classes in which the features are independent of each other and have only one dimension,where the mean is shifted.Given four indicator sets,C1,C2,C3andC4,fori∈Ck,xij∼N((k−1)/3,1) ifj≤100 andxij∼N(0,1) otherwise.The one-dimensional projection of the data fully captures the structure of the class. For each method,the models were fitted to the training set using a range of values for the tuning parameters.Tuning parameter values were chosen to minimize errors in the validation set.The parameters estimated for the training set were then evaluated for the test set.After obtaining the estimated discriminant vectors,we applied the KNN method to the new dataset to perform classification.This process was repeated 200 times. The classification error in the test set and the number of non-zero features used by the discriminant vectors are listed in Table 1.In the “errors” row of each simulation result,the average number of misclassified individuals on the test set with 900 observations is presented,and the standard deviation is in parentheses.Correspondingly,in the “features”row,the average number of non-zero features used in estimating the discriminant vectors is reported,with the standard deviation in parentheses.As shown in Table 1,our method has a smaller error when the number of features used is almost equal.Moreover,it is easier to adjust the parameters using theℓ0penalty method. This section compares our SLDA-BESS method with three existing methods: penalized LDA-ℓ1,NSC,and RDA. We applied the four methods to the three gene expression datasets. Ramaswamy dataset[13]: A dataset consisting of 16063 gene expression measurements and 198 samples belonging to 14 distinct cancer subtypes. Nakayama dataset[14]: A dataset consisting of 105 samples from 10 types of soft tissue tumors,with 2 2283 gene expression measurements per sample.We shall limit the analysis to five tumor types with at least 15 samples in the data,resulting in a subset of data containing 86 samples. Sun dataset[15]: A dataset consisting of 180 samples and 54613 expression measurements.The sample falls into four classes: one non-tumor class and three glioma classes. Each dataset is split into a training set containing 75% of the samples and a test set containing the remaining 2 5% of the samples.A total of 100 replications were performed,each with randomly selected training and testing sets.The results are presented in Table 2.The results suggest that the four methods perform roughly equally in terms of error,but our SLDA-BESS method utilizes fewer features.Moreover,our SLDA-BESS method is more suitable for remarkably sparse models,whereas the other three methods may fail when using a few features. Table 1.Simulation result. Table 2.Results obtained on three different gene expression datasets. Linear discriminant analysis is a commonly used classification method.However,it fails if the number of features is large relative to the number of observations.This study extended LDA to a high-dimensional setting by adding an ℓ0penalty to produce a discriminant vector involving only a subset of features.Our extension is based on Fisher’s discriminant problem,such as a generalized eigen problem,and then uses the SLDA-BESS algorithm,which combines the naive algorithm and the exchange step to solve the sparse discriminant vector.Sparse discriminant vectors were generated whilemaking the classifier more interpretable in practical situations.The results of both numerical simulations and analysis of real data demonstrate the superior performance of our SLDA-BESS method.The convergence rate and complexity of the SLDA-BESS algorithm,as well as the theoretical properties of the minimax lower and upper bounds of the estimator,can be further considered in the future. Acknowledgements This work was supported by the National Natural Science Foundation of China (71771203). Conflict of interest The authors declare that they have no conflict of interest. Biographies Qi Yinis currently a graduate student at the University of Science and Technology of China.His research interests focus on variable selection. Lei Shuis currently a Ph.D.student at the University of Science and Technology of China.His research interests focus on high-dimensional statistical inference,including variable selection,change point detection,and factor analysis.

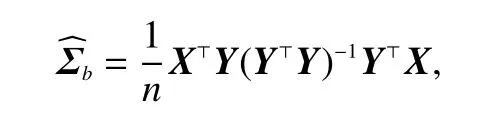



2.2 Sparse linear discriminant analysis



2.3 Best subset selection




3 Numeric studies
4 Real data analysis


5 Conclusions
- 中国科学技术大学学报的其它文章
- Pure state tomography with adaptive Pauli measurements
- Non-Hermitian skin effect in a spin-orbit-coupled Bose-Einstein condensate
- Intersection complex via residues
- Boosting photocatalytic Suzuki coupling reaction over Pd nanoparticles by regulating Pd/MOF interfacial electron transfer
- Three-dimensional tubular carbon aerogel for supercapacitors
- An advance selling strategy with a trade-in program

