Pure state tomography with adaptive Pauli measurements

Xiangrui Meng ,Minggen He ,and Zhensheng Yuan

1Hefei National Research Center for Physical Sciences at the Microscale and School of Physics,University of Science and Technology of China,Hefei 230026,China;

2CAS Center for Excellence in Quantum Information and Quantum Physics,Hefei 230026,China

Abstract: Quantum state tomography provides a key tool for validating and fully exploiting quantum resources.However,current protocols of pure-state informationally-complete (PS-IC) measurement settings generally involve various multiqubit gates or complex quantum algorithms,which are not practical for large systems.In this study,we present an adaptive approach to N-qubit pure-state tomography with Pauli measurements.First,projective measurements on each qubit in the Z-direction were implemented to determine the amplitude of each base of the target state.Then,a set of Pauli measurement settings was recursively deduced by the Z-measurement results,which can be used to determine the phase of each base.The number of required measurement settings is O(N) for certain quantum states,including cluster and W states.Finally,we numerically verified the feasibility of our strategy by reconstructing a 1-D chain state using a neural network algorithm.

Keywords: quantum information;quantum state tomography;Pauli measurement;neural network

1 Introduction

In the recent decades,prodigious advances in quantum information technology have been achieved. As quantum devices in laboratories reach tens of entangled qubits,validating the correctness of their performance has become challenging[1].Quantum state tomography (QST),one of the most commonly used validation methods,aims to provide a complete estimate of the quantum states[2].QST reconstructs an unknown quantum state from measurement results under a set of informationally-complete (IC) measurement settings[2−4].For ad-dimensional system,d2positive operator-valued measures (POVM) are necessary for general state tomography[5],thereby making the measurement process and data post-processing time-consuming.

To overcome this obstacle,prior information is used to restrict the unknown state to a more limited space,such as the pure state (PS) space[5−7].Owing to the shrinkage of the degrees of freedom,various redundancies in the IC measurement settings can be removed for PS tomography.Several protocols have been proposed for the design of PS-IC measurement settings[5,7−9].However,these methods generally involve multi-qubit gates or complex quantum algorithms,making PS tomography a technically difficult task.An experimentally friendly strategy with minimal Pauli measurement settings for two-and three-qubit systems has been proposed[10].This strategy offers a promising direction in developing a feasible and general PS-IC measurement strategy for larger systems.

In this study,we propose an adaptive strategy for the design of IC Pauli measurement settings for arbitraryN-qubit PS.First,projective measurements of each qubit in theZdirection were implemented to detect prior information of the target state,and the amplitude of each base of the target state was determined.Then,a set of Pauli measurement settings was designed based on the detected prior information,which offers a set of equations to determine the phase of each base.The informational completeness of the strategy is guaranteed by the completeness of these equations.Because no multiqubit gates or complex quantum algorithms are involved,our strategy offers a feasible approach to PS tomography for experiments.

The remainder of this paper is organized as follows.In Section 2,we first formulate the PS-IC problem and divide it into the determination of the amplitude and the phase of each base of the target state.Then,we prove the existence of Pauli measurement settings that can be used to determine the phase of each base.Finally,we provide a strategy to practically select the measurement settings for arbitrary PSs.In Section 3,we numerically reconstruct a 1-D chain state with a restricted Boltzmann machine (RBM) model to verify the feasibility of our strategy.Moreover,we used the measurement error mitigation configuration with the RBM model to improve the accuracy of the state reconstruction. A brief summary is provided in Section 4.

2 Design of adaptive IC Pauli measurement settings

wherepiis the relative frequency of theith base in the measurement results.In addition,we can deduce the support set A of the target state from the measurement results,that is,the set of bases with non-zero amplitude.The next step involves determining the phase of each base using the measurement results from the other measurement settings.In fact,owing to global phase symmetry,only |A|−1 independent relative phases need to be determined.

In the remainder of this section,we first prove that for an arbitrary PS,there exists a set of Pauli measurement settings that can be used to determine the phase of each base.We then propose a strategy for selecting the measurement settings to minimize the experimental errors originating from the measurements in theX-orY-directions.

2.1 Existence of IC Pauli measurement settings

We denote the single-qubit Pauli operators as σx=X,σy=Y,σz=Z.For simplicity,we omit the tensor product symbol by writing e.g.XYinstead ofX⊗Y. H(N),which is composed of 2Nelements,is denoted as the set of bases forNqubit system in a standardZ-basis representation.Then,we can define the distance between the elements in H (N) as

and | αN−n〉=|βN−n〉.We can use projective measurements in theZ-direction on theseN−nqubits to project the state into the space spanned by H(n). Consequently,we can determinewith the measurement settings designed in H(n),which returns the problem to Case (i) or Case (ii).This recursion results in Case (i) with the reduction in dimensionality.Finally,we obtain a set of measurement settings for determining.

2.2 Selection strategy

Although we have proven the existence of IC Pauli measurement settings for arbitrary PSs,the solution to this problem is not unique.For different experimental implementations,we optimize the selection of the measurement settings.To minimize the system errors originating from the experimental operation of measurements in theX-andY-directions,we propose a strategy to select the measurement settings.

First,we define the cluster as a set of bases in which the relative phase of each pair of bases has already been determined.We define the distance between clusters P and Q as follows:

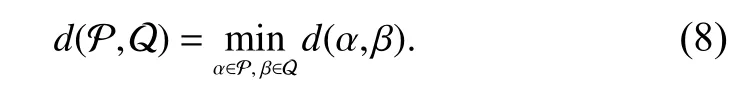
Our strategy involves the following steps.We begin with the initial condition that each base in A is a cluster itself;then,we iteratively execute the following steps until all of the elements in A belong to the same cluster:

(i) We first split A into different clusters,that is,We can select the two closest clusters Apand Aqusing

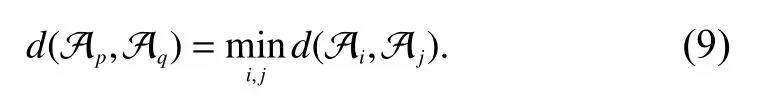
(ii) We find two bases α and β that satisfy

Using the method introduced in Section 2.1,we can deduce the measurement settings for determining.

(iii) The measurement settings selected in Step (ii) can typically be used to determine the relative phases of more than one pair of bases;therefore,we need to regroup the clusters in this step.This leads the procedure back to Step (i).

Finally,we obtain a set of measurement settings that can be used to determine the phase of each base of the target state with the fewest single-qubit operations.Several examples are provided as follows.ForN-qubit cluster states,the support set is A=H(N).The measurement settings can be deduced as

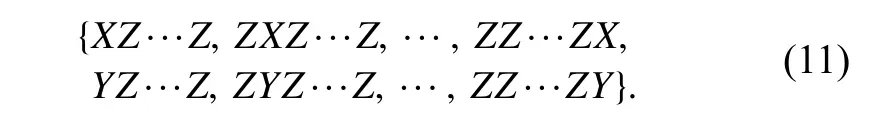
For the GHZ states,the Pauli measurement settings are{XX···XX,YX···XX},which corresponds to Case (i) in Section 2.1.ForWstates,the measurement settings can be deduced from the symmetry of the bases as[11]

3 Numerical simulation of pure state reconstruction

In this section,we numerically reconstruct a 1-D chain state using the RBM model to verify the feasibility of our strategy.In addition,we use a measurement error mitigation configuration based on the RBM model to improve the accuracy of state reconstruction[1,12,13].

3.1 Introduction to the RBM model

Although the target state |ψ〉 can,in principle,be inferred from the set of equations generated by the strategy,solving a multivariable system of equations is a time-consuming task.The RBM is a classical generative machine-learning model that can be used to capture the structure of the distribution contained in the samples[14,15].Its application in quantum state reconstruction has been proven to be a state-of-the-art method[12,16].TheN-qubit quantum state |ψ〉 is represented by two coupled RBM models,which can be expressed as[12]

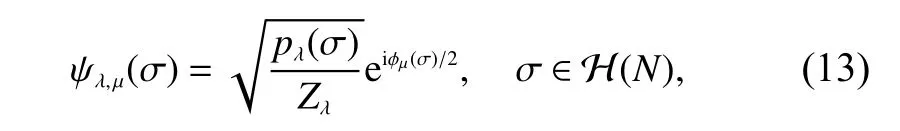
wherepλand ϕµare two independent RBM configurations that separately represent the amplitude and the phase of each base.The RBM ansatz function is[14]

whereU(σα,σ) is the unitary transformation of basis change.The parameters of the RBM model can be fitted from the measurement results using the contrastive divergence learning algorithm[14],leading to a parameterized representation of the target state.

To numerically simulate the preparation and measurement process of the target state,we developed the Python package Qusource①https://github.com/Meng-Xiang-Rui/Qusource.We trained the target state using an open-source library QuCumber[17].

3.2 Measurement error mitigation

The measurement process contains readout errors,which can reduce the accuracy of the reconstruction results.Therefore,a measurement error mitigation procedure should be implemented before state reconstruction.Here,we take the measurement process involving bit-flip errors as an example,and use an error-mitigation configuration with the RBM model to improve the accuracy of state reconstruction[1].We denotepidealas the ideal probability distribution under a certain measurement setting andpexpas the distribution of the measurement results involving bit-flip errors.Assuming that the measurement process for each qubit is independent,we obtain the transfer matrix of this process,that is,.Here

To solve this problem,we can use the maximum likelihood estimation (MLE) method,which takes the likelihood function as the cost function.Owing to its universality,the RBM model is a good candidate for the MLE method[1,18].

We compare the linear inversion and MLE methods in the reconstruction of the target state amplitude involving an error rate ε=0.01.The results are evaluated based on the fidelity between the probability distributionqiand ideal distribution|ci|2,that is,

As shown in Fig.1,the processed measurement results using the RBM model are close to the measurement results without errors. The difference between their fidelities is∆FRBM=0.01±0.0045,which is notably better than that between the processed measurement results involving the linear inversion method (∆Finv=0.074±0.001) and measurement results without processing (∆Ferror=0.10±0.005).

3.3 Reconstruction of a 1-D chain state

In this section,we apply our strategy to reconstruct a 10-qubit 1-D chain state.The entanglement feature of this state is important in optical lattices[19].We numerically reconstruct this state using the RBM model[12].

The quantum circuit of the preparation process[19]of a 10-qubit 1-D chain state is shown in Fig.2.The preparation process begins with the Néel state |0101010101〉[19]. Then,gates are imposed on the qubits at (2k−1,2k),1 ≤k≤5.Here

Fig.1.Single-qubit flip error mitigation.The target state is the 10-qubit 1-D chain state,which is introduced in Section 3.3. The results(m ean±std) are evaluated using Eq.(19) from five independent numerical experiments.The blue points represent the ideal measurement results without errors.The yellow triangles represent the measurement results with flip errors (ϵ =0.01),which are simulated by the bit-flips in the randomly chosen data points of the ideal measurement results.The red squares represent the processed measurement results with the RBM model.The green squares represent the processed measurement results with the linear inversion method.

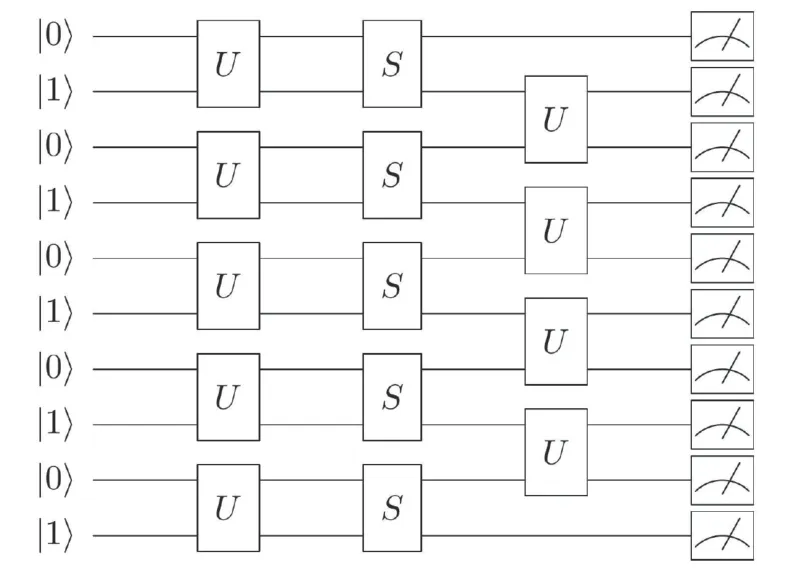
Fig.2.Quantum circuit of a 10-qubit 1-D chain state preparation process.The initial state involves the Néel state;the notation U and S stand for gate and the STO process,respectively.

To verify the feasibility of these measurement settings,we implement the reconstruction of the target state using the RBM model under different measurement times.The results are evaluated using the fidelity between the reconstructed quantum and target states,that is,

Fig.3 shows the sequence of fidelities are convergent to 1,which numerically proves the feasibility of our measurement strategy.

4 Conclusions

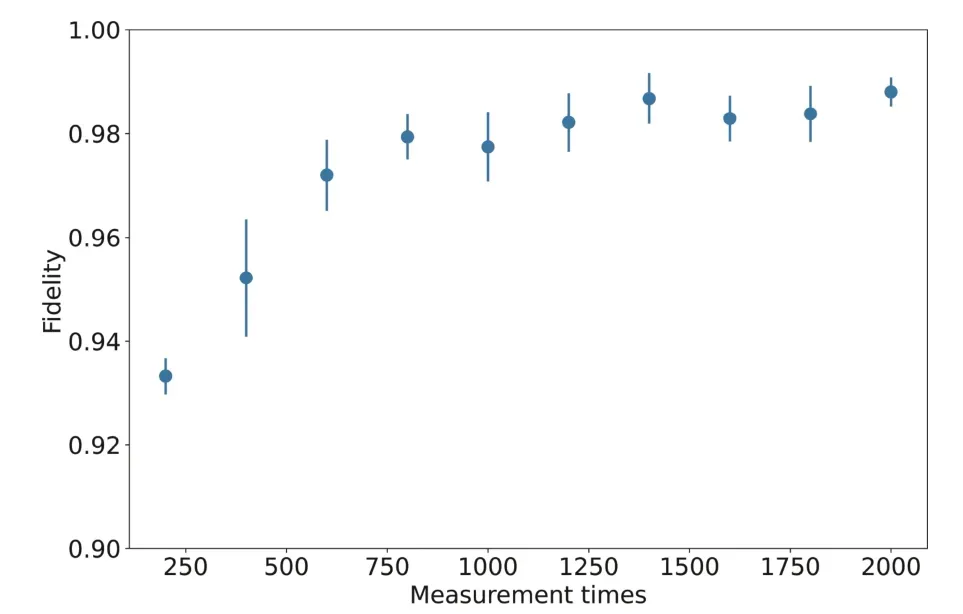
Fig.3.Reconstruction of 1-D chain state with the RBM model.The results (m ean±std) are evaluated using the fidelity between the target and reconstructed states with the RBM model in five independent numerical experiments.

In this work,we presented an adaptive strategy for the design of PS-IC measurement settings with Pauli measurements,and numerically verified its feasibility by reconstructing the a 10-qubit 1-D chain state with the RBM model.We demonstrated that for an arbitrary pure quantum state,there exists a set of Pauli measurement settings that fulfills the IC condition.This was proven by the fact that the relative phase between any two bases of the target state can be recursively determined by the relative phases of some intermediate bases using Pauli measurements.Based on this proof,we proposed a strategy for selecting a set of IC Pauli measurement settings.We verified the feasibility of our strategy by reconstructing the a 1-D chain state with the measurement settings designed based on this strategy.The fidelities of the reconstruction results converged to 1 with increasing measurement times,thus proving the feasibility of our strategy.In addition,we used the MLE method to implement the procedure of measurement error mitigation,which can improve the accuracy of state reconstruction.

Our strategy provides a feasible approach to PS tomography using Pauli measurements. In addition,our work raises several open questions.For example,what is the upper boundary of the number of measurement settings in our selection strategy? Does a general selection strategy exist forO(N)Pauli measurement settings? How can we determine the minimal set of Pauli measurement settings for an arbitrary state?These questions suggest avenues for future research explorations that might turn PS tomography into a more practical experimental tool.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (12125409).

Conflict of interest

The authors declare that they have no conflict of interest.

Biographies

Xiangrui Mengis currently a graduate student under the tutelage of Prof.Zhensheng Yuan at the University of Science and Technology of China.His research interests focus on quantum information and quantum computation.

Zhensheng Yuanis now a Professor of Physics at the Hefei National Research Center for Physical Sciences at the Microscale,University of Science and Technology of China (USTC),and a winner of the National Science Fund for Outstanding Youth.He received a B.Sc.and a Ph.D.from USTC in 1998 and 2003,respectively.During 2006 to 2011,he had been working at the Heidelberg University as a PostDoc,an Alexander von Humboldt Fellow,and a senior scientist (when he was a CoPI of a couple of projects) successively.He took his professorship at USTC in 2011.His research field is quantum manipulation of light and cold atoms.Highlights of his research achievements include the quantum simulation of mechanisms in LGT and the manipulation of atomic spin entanglements in optical lattices.He has about 70 publications in peer-reviewed journals includingNature,Science,Nature Physics,andPhysical Review Letters.