Intersection complex via residues

Xiaojin Lin

School of Mathematical Sciences,University of Science and Technology of China,Hefei 230026,China

Abstract: We provide an intrinsic algebraic definition of the intersection complex for a variety.

Keywords: algebraic geometry;intersection complex;weight filtration

1 Introduction

Intersection homology theory is a generalization of singular homology for singular algebraic varieties.In Ref.[1],Sheng and Zhang established a positive characteristic analog of an intersection cohomology theory for polarised variations of Hodge structures and proposed an algebraic definition of the intersection complex,but with the help of coordinate systems.Here,we provide an intrinsic definition of the intersection complex via residues and provide a geometric description of it.

The remainder of this paper is organized as follows.Section 2 establishes notations and presents key definitions.Section 3 provides the main theorem and its proof.Finally,in Section 4,an explicit computation following the spirit of proof in surface case is made,and a counterexample is discussed.

2 Intersection complex

whereli:ε →ε|Diis the canonical restriction map.

Now we can define the intersection complex.Set

Proof of Lemma 2.1.It is a local problem,we may assumeX=SpecAand F =M˜ ,whereAis a reduced commutative local ring with maximal ideal m andMis a finiteAmodule.

We only have to showMis a freeA-module.Assume thatk(m) vector spaceM/mMhas dimensionn. We use Nakayama’s lemma to lift the basis forM/mMinto a set of generatorsm1,m2,···,mn. It is sufficient to demonstrate thatmiis linearly independent. Suppose thatwhereai∈A. In addition,aimust lie in m for alli,because the generatorsmiform the basis of the fibreM/mM. Choose q ∈SpecAarbitrarily;then,the images ofmiinMq/qMqgenerate vector space.In addition,ϕ is constant,implying that they are,in fact,a basis,similarly toai∈q for alli.

Therefore,ailies in the intersection of the prime ideals ofA,which is the nilradical ofA,and thusai=0 becauseAis assumed to be reduced.This completes this proof.

It is interesting to investigate the case where (ε,∇) comes from the polarized variation of Hodge structures.Let us consider a quick recall of this (cf.Ref.[3]).IfXis a complex variety,andEis a local system overX−Dunderlies a polarized variation of Hodge structures,then we obtain a vector bundle (ε,∇) equipped with a flat connection via a Riemann-Hilbert correspondence overX−D.There is a canonical extension of ε to a vector bundle with a logarithmic flat connection overX,with the residue of the connection along divisorDibeing the log of the monodromy of the divisor (up to a scalar),which we denote asNi.It can be observed thatNiis topologically defined.

Note that the residue of the connectionis exactly (up to a scalar) the endomorphismNIif it is restricted to the stratumDI.It can be easily seen that the res-intersection complex coincides with the intermediate extension complex.From this perspective,we provide an algebraic definition of the intermediate extension complex.

3 Main theorem

In the following,we show that the res-intersection subcomplex above coincides with the intersection subcomplex defined in Ref.[1].

LetX,D,ε be as in the previous section.Given a coordinate system

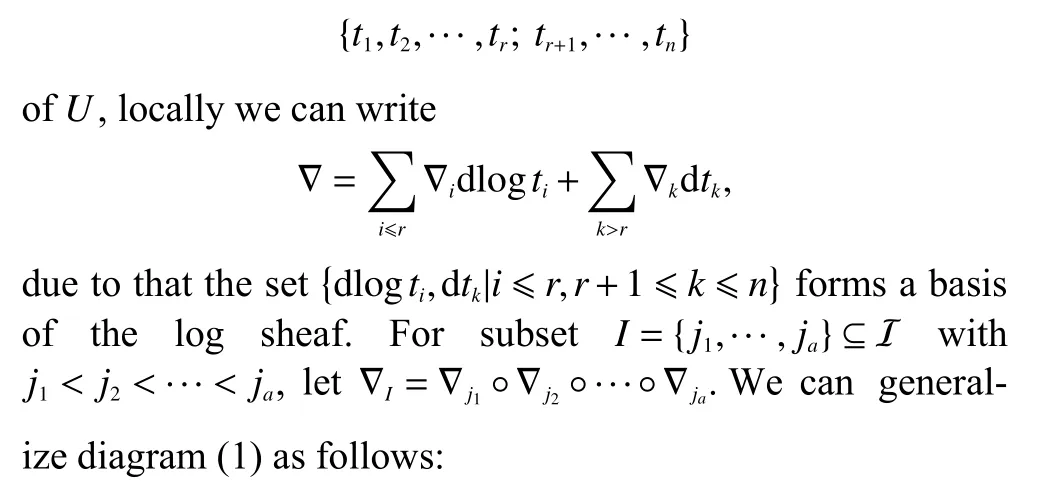
Remark 3.1.The first sublemma illustrates that weight equals to the number of times of the irreducible components of the divisor intersect (in other words,the depth of the stratification). The second provides a local description of the weight filtration along divisor in terms of the coordinates.

We now return to the proof of the main theorem.

Proof of Theorem 3.1.Without loss of generality,we assume thatr=n.

4 Surface case

In this section,we provide an explicit calculation for the surface case and present an example to the main theorem without bundle morphism conditions.

LetX=Spec(k[t1,t2]) be a surface and letD=D1+D2defined byt1t2=0.The divisor gives rise to a stratification the

In the sequel of the section we will present an example,which is provided by Zebao Zhang,to show that the main theorem will be wrong if the residue morphisms are not assumed to be bundle morphisms.Letkbe a perfect field of characterp,(X,D) is as above.Define logarithmic connection over

Acknowledgements

I would especially like to thank Prof.Mao Sheng for his suggestions.And I would also like to thank Dr.Zebao Zhang for correcting the article.

Conflict of interest

The author declares that he has no conflict of interest.

Biographies

Xiaojin Linis currently a graduate student under the tutelage of Prof.Mao Sheng at the University of Science and Technology of China.His research interests focus on Hodge theory and vector bundle.