Non-Hermitian skin effect in a spin-orbit-coupled Bose-Einstein condensate

Haowei Li,Xiaoling Cui ,and Wei Yi,4

1CAS Key Laboratory of Quantum Information,University of Science and Technology of China,Hefei 230026,China;

2Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China;

3Songshan Lake Materials Laboratory,Dongguan 523808,China;

4CAS Center for Excellence in Quantum Information and Quantum Physics,Hefei 230026,China

Abstract: We study a Bose-Einstein condensate of ultracold atoms subject to a non-Hermitian spin-orbit coupling,where the system acquires the non-Hermitian skin effect under the interplay of spin-orbit coupling and laser-induced atom loss.The presence of the non-Hermitian skin effect is confirmed through its key signatures in terms of the spectral winding under the periodic boundary condition,the accumulation of eigen wavefunctions at boundaries under an open boundary condition,and bulk dynamics signaled by a directional flow.We show that bulk dynamics,in particular,serves as a convenient signal for experimental detection.The impact of interaction and trapping potentials is also discussed based on the non-Hermitian Gross-Pitaevskii equations.Our work demonstrates that the non-Hermitian skin effect and its rich implications in topology,dynamics,and beyond are well within the reach of current cold-atom experiments.

Keywords: non-Hermitian physics;open systems;non-Hermitian skin effect;ultracold atoms

1 Introduction

The non-Hermitian skin effect is an intriguing phenomenon in open systems,in which eigen wavefunctions exponentially localize near boundaries[1].It has a profound impact on a wide range of properties of an open system: while the non-Hermitian skin effect directly modifies the topology,spectral symmetry,and bulk dynamics in systems described by non-Hermitian effective Hamiltonians[1−13],it also manifests in the long-time density-matrix dynamics driven by the master equation[14,15].Over the past three years,the non-Hermitian skin effect and its many consequences have been experimentally confirmed in classical or photonic systems[16−21],but not in a quantum many-body environment.

In recent studies,it has been pointed out that the non-Hermitian skin effect can be induced by non-Hermitian spinorbit coupling in cold atoms[22,23]. Therein,two hyperfine ground states of an atom are coupled by a two-photon Raman process,under which a spin flip is accompanied by a change in the atomic center-of-mass momentum. Such coupling between the atomic spin and external orbital degrees of freedom has been the subject of intense study over the past decade[24−29],because of its highly non-trivial influence over the system band topology[30],as well as the possibility of inducing exotic few-and many-body states[31−35].In a very recent experiment,a Raman-induced spin-orbit coupling was further dressed by laser-induced atom loss[36].For this purpose,an additional laser selectively couples one of the hyperfine spin states to an electronically excited state that is subsequently lost under spontaneous emission[37].For atoms that remain,their dynamics is driven by a non-Hermitian Hamiltonian featuring a non-Hermitian spin-orbit coupling and spectral singularity.While the experiment focused on the chiral parametric transport close to the spectral singularity known as the exceptional point,theoretical studies have revealed the hidden non-Hermitian skin effect under the same configuration[22,23].However,questions remain regarding amenable detection schemes,as well as the impact of interaction and trapping potentials that are present under typical experimental conditions.

In this work,we address these questions by studying a Bose-Einstein condensate of cold atoms under the recently realized experimental setup.First,we confirm the results in Refs.[22,23],demonstrating the spectral winding and accumulation of eigen wavefunctions at boundaries by solving a single-body problem.In particular,under the periodic boundary condition (PBC),the single-body eigenspectrum of a finite-size system features closed loops on the complex plane.Whereas under the open boundary condition (OBC),the eigenspectrum reduces to open arcs within the loops.Such is the topological origin of the non-Hermitian skin effect[8,9].We then demonstrate the directional dynamics of wave packets in a homogeneous condensate with interactions turned off,that is,the wavefunction propagates along the direction of the non-Hermitian spin-orbit coupling. This unidirectional propagation is the direct consequence of a persistent bulk current,which is the driving force behind the namesake phenomenon of the non-Hermitian skin effect—the accumulation of wavefunctions at boundaries.Note that in our system,the bulk current,or the non-Hermitian skin effect,is due to the interplay of spin-orbit coupling and atom loss,which can be related to models with non-reciprocal inter-spin coupling through a spin rotation.

The unidirectional bulk dynamics offers a convenient signal for the detection of the non-Hermitian skin effect,both for a homogeneous condensate and,more importantly,for a trapped one.We illustrate this by calculating the growth rate of the condensate[11,38],which,in a homogeneous setup,corresponds to the Lyapunov exponent in the infinitely long-time limit.At finite times,the growth rates provide a qualitative measure of the Lyapunov exponent,and more importantly,can characterize the non-Hermitian skin effect.In particular,the peak location of the growth rate (the so-called shift velocity) characterizes the propagation of the condensate wavefunction.We show that in the presence of a trapping potential,a condensate initialized in the ground state at the trap center would flow along the direction of the non-Hermitian spinorbit coupling,either in the same direction or opposite to that of the momentum transfer.The condensate wavefunction is squeezed and eventually localized off-center,balanced by the higher potential energy towards the trap edge.We further consider the impact of mean-field interactions on the unidirectional flow,and demonstrate that a repulsive (attractive)interaction enhances (suppresses) the average velocity of the flow,suggesting a stronger (weaker) non-Hermitian skin effect for a repulsively (attractively) interacting condensate.Our results illustrate bulk dynamics and growth rate as viable signals for the experimental detection of the non-Hermitian skin effect in cold atoms.Based on the flexible controls therein,it would be exciting to further explore the impact of the non-Hermitian skin effect on the quantum many-body system of cold gases.

The remainder of this paper is organized as follows: In Section 2,we present the model and characterize its singlebody properties.We study the bulk dynamics of the condensate in Section 3,both with and without trapping potentials,by evolving the Gross-Pitaevskii equations.In Section 4,we investigate the impact of interactions on the non-Hermitian skin effect.We summarize the study in Section 5.

2 Model

We consider the recently implemented non-Hermitian spinorbit coupling in cold atoms[36],where the single-body Hamiltonian is given by

The non-Hermitian Hamiltonian governs the conditional dynamics of the Lindblad equation dρ/dt=ΓzSρS†,where ρ is the atomic density matrix,andSis the quantum jump operator describing the laser-induced,spinselective loss.Specifically,the dynamics of the system is driven by the non-Hermitian HamiltonianH,when the quantum jump terms are dropped[39].Experimentally,such a conditional dynamics is implemented by probing only the atoms that remain in the system.The description is exact in the absence of interactions and when the spontaneous emission back into the two hyperfine spin states can be neglected.

While the experiment focuses on the parity-time symmetry and spectral singularity (the exceptional point) of the Hamiltonian (1),the system also has the non-Hermitian skin effect,despite being a continuous model.To confirm this,we calculate the single-particle eigenspectra of Eq.(1) under both PBC and OBC,for a one-dimensional gas along thezdirection,which is the direction of the spin-orbit coupling.

For a one-dimensional gas,the single-particle eigenspectrum in the momentum space is given by

whereEk=2k2/(2m),andkis the momentum along thezdirection.The eigenspectrum corresponds to the green curves in Fig.1,where the two branchesE±(k) are self-connected at infinite |ReE|,forming closed loops on the complex energy plane.For a finite system but still under PBC,the loop structures are easier to observe (blue curves).This is consistent with the spectral winding,which is the topological origin of the non-Hermitian skin effect.By contrast,under an OBC,the eigenspectra collapse into open arcs (red curves) within the spectral loop under the PBC.Correspondingly,the spatial distribution of the eigen wavefunctions accumulates at the open boundary,as shown in Fig.1b.Here the position of the localization (the left or right boundary) is tunable through the parameters of the spin-selective loss or the spin-orbit coupling.Note that we denote the wavefunctions for the two spin species as φ1,2(z),which are normalized according to

3 Dynamic signal of the non-Hermitian skin effect

In cold atomic gases,a sharp open boundary is typically difficult to engineer,and the eigenspectrum is not easy to probe,unlike in classical or photonic simulators.Therefore,the most prominent signatures of the non-Hermitian skin effect,as demonstrated in Fig.1,can be experimentally elusive.However,systems with non-Hermitian skin effects also possess unique signatures in the bulk dynamics,which,as we reveal in this section,serve as convenient dynamic signals of the non-Hermitian skin effect.

Fig.1.(a) Single-particle eigenspectra of Hamiltonian (1) on the complex plane.Green: eigenspectrum of in the momentum space (an infinite system under PBC). Blue: eigenspectrum of a finite system with z ∈[−30,30].Red: eigenspectrum under OBC.Inset: enlarged eigenspectra.We fix Ω=0.5Er and Γz=2Er.For calculations of finite systems,the spatial coordinates along z are discretized into 480 segments.(b) Spatial distribution of the 100 eigenstates with the smallest real components (indicated by the color bar).

We first consider the non-interacting case,where the postselection principle underlying the non-Hermiticity of the Hamiltonian is valid,and the atoms that remain in the system evolve according to (1).In Fig.2a,we show the numerically simulated propagation of the condensate wavefunction.The initial state is a Guassian wave packet ψ1,2(x,y,z;t=0)∝exp[−(x2+y2+z2)/w2],withw=3 and normalized to unity.We evolve the wavefunction in real space using the Schrödinger’s equation

where ψ1,ψ2are the wavefunctions of the two spin species.For numerical calculations,we discretize the spatial coordinates alongzinto 480 segments in the rangez∈[−30,30] and those alongxandyinto 32 segments in the rangex,y∈[−12,12].The spatial derivatives in the Hamiltonian are then translated into finite differences.

In Fig.2a,we show the evolution of the wavefunction along thez-axis with (x=0,y=0).The directional propagation of the wavefunction suggests a persistent bulk current that lies at the origin of the non-Hermitian skin effect.In previously studied lattice models,the non-Hermitian skin effect was often associated with non-reciprocal hopping[1].It is important to note that the non-Hermitian spin-orbit coupling with a manifestly spin-selective lossis related to a non-reciprocal model through a spin rotation

To provide a quantitative measure of the unidirectional propagation,we define the wavefunction growth rate as

wherevdenotes the shift velocity.In the long-time limitt→∞,the growth rate converges to the Lyapunov exponent of a homogeneous system[11].As shown in Fig.2b,the peak of λ(v,t) lies at a finite shift velocityvm≈19.1 att=0.7,which is essentially the average propagation velocity of the wavepacket peak in Fig.2a at the given time.By contrast,with vanishing spin-orbit coupling (Ω =0) or atom loss (Γz=0),the growth rate peaks atvm=0 (see Fig.2c,d) att=0.7,indicating the absence of bulk current and non-Hermitian skin effect.Note that without a trapping potential,the peak location of λ(v,t) already converges to a finitevmin our numerical simulations of a finite-time evolution.

Fig.2.(a) Propagation of the condensate wavefunction in the bulk,withΩ=0.5Er and Γz=2Er.(b) Growth rate as a function of the shift velocity under the parameters of (a).(c) Growth rate with Ω =0 and Γ z=2Er,evaluated at t=0.7. (d) Growth rate with Ω=0.5Er and Γz=0,valuated at t=0.7. The unit of time is 1 /ω0=10 ms.

Experimentally,condensates are typically subject to a harmonic trapping potential,which provides a natural boundary,though not as sharp as that of an ideal OBC.For a condensate initialized in the ground state,that is,near the center of the trap,we expect the directional flow to persist in systems with the non-Hermitian skin effect.However,when the condensate moves off-center,the soft boundary provided by the harmonic trap impacts the wavefunction propagation and eventually stops it near the edge of the trap.

Such an intuitive picture is indeed confirmed in Fig.3,where the dynamics is governed by

First,in Fig.3a,d,we show the typical spatial distribution(along thez-axis) of eigenstate wavefunctions forH+V(r),with trapping frequencies ω=ω0and ω=2ω0,respectively.The off-center distribution is a direct manifestation of the non-Hermitian skin effect in a harmonic trap.

We then numerically evolve the ground state,where a directional propagation of the wavefunction is observed [see Fig.3b,e],consistent with the dynamics in the homogeneous case of Fig.2.However,in a trapping potential,the directional propagation slows down,and is eventually stopped by the trap edge,which is apparent by comparing the dynamics under different trapping frequencies (see Fig.3b,e).What we observe here is essentially the dynamic accumulation of wavefunctions at boundaries,driven by the non-Hermitian skin effect.Under our parameters (taken from typical87Rb experiments),starting with a condensate of 5×105atom,the final atom number att=0.6 (∼6 ms) is estimated to be ∼60 for Fig.3b,and ∼100 for Fig.3e. Alternatively,att=0.4(∼4 ms),the remaining atom number is ∼103for both cases,while the directional propagation is still visible in Fig.3b,e.

Fig.3.(a,d) Spatial distribution of eigen wavefunctions along the z direction in an isotropic harmonic trap,with Ω=0.5Er and Γ z=5Er.For the numerical calculations here,we take a cylindrical coordinate,discretizing z ∈[−30,30] into 480 segments,and the radial coordinate ρ ∈[0,4] into 8 segments.We plot the radial-∫integrated spatial distribution of the 800 eigenstates with the smallest real components,colored according to R e(E) (see color bar).Specifically,(z)=2π ρdρψ1(ρ,z).(b,e) Propagation of the condensate wavefunction in the bulk.(c,f) Growth rate as a function of the shift velocity at t=0.6.The peak shift velocity v m ≈16.04 in (c) and v m ≈13.33 in (f).The trapping potential is ω=ω0=100 Hz in (a,b,c),and ω=2ω0=200 Hz in (d,e,f).The unit of time is 10 ms,so the longest evolution time in (b,e) is 6 ms.

In Fig.3c,f,we show the growth rates under different trapping frequencies.At short times,the growth rate peaks at a finitevm,consistent with the presence of the non-Hermitian skin effect.After a sufficiently long time (t≳0.37 under our parameters),another peak emerges in λ (v,t) see Fig.3f,indicating the backflow of condensate atoms,as they are reflected from the boundary (the boundary to the right in this case).Such an effect is more apparent for deeper traps,as illustrated in Fig.3c,f.Following a sufficiently long time evolution (not shown),the peak velocityvmof the growth rate uniformly drops to zero,as the propagation is stopped by the boundary.As the time required forvmto vanish is typically much longer thant=0.7 (∼7 ms),the vanishing ofvmis difficult to be observed directly due to the small number of remaining atoms at long times.

As such,a trapped condensate offers an intriguing scenario for the dynamic detection of the non-Hermitian skin effect,where the short-time dynamics is dominated by the directional bulk current,whereas the long-time dynamics is dominated by the accumulation of atoms towards the boundary.

4 Interaction effect

We now consider the impact of interactions,particularly on the dynamic signal of the wavefunction propagation.While the non-Hermitian description based on post-selection can be questionable when interatomic interactions are considered,we assume that the condensate is always in a coherent state,which is an eigenstate of the jump operator and hence a stead state of the dynamics.This is a good approximation under weak interactions when the quantum depletion is small.It also requires that there are still a significant number of atoms in the condensate,despite the constant atom loss.We may then write the Gross-Pitaevskii equation as

with the mean-field interaction term given by

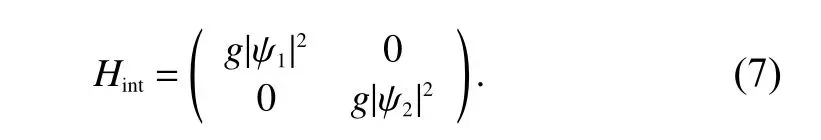
Heregis the interaction rate,and we have neglected interspecies interactions.For our numerical simulations,the unit of the interaction rate is taken asg0=4π2as/m,whereas=100a0(a0is the Bohr radius).We initialize a condensate ofN=5×105atoms,in the absence of atom loss and spinorbit coupling.This is achieved using an imaginary time evolution.During the time evolution,the atomic number continuously decreases owing to the atom loss.The interaction effect therefore also becomes diminishingly small over time.

In Fig.4a,we show the numerically simulated average velocity of the wavefunction propagation along thez-axis with(x=0,y=0),which is defined as

where we fixt=0.7 for the time evolution.When the trapping frequency vanishes,the average velocity converges,regardless of the interaction strengthg.This is consistent with the convergence ofvmin Fig.2a,b.By contrast,for a sufficiently large trapping frequency (or a sufficiently long evolution time),vanishes,indicating the accumulation of wavefunction at the trap edge,which is consistent with the results in Fig.3.More importantly,a repulsive (attractive) interaction facilitates (suppresses) the wavefunction propagation,as indicated by Fig.4a.This is direct evidence of the interplay between interactions and non-Hermitian skin effects.The interaction effect is also more apparent under larger trapping frequencies owing to the increased average density.

Fig.4. Effect of condensate interaction on the non-Hermitian skin effect in a trapped gas,evaluated at t =0.7 (∼7 ms).See main text for the definition of the average propagation speed v ¯ in (a),and the integrated propagation speed in (b).Other parameters are the same as those in Fig.3.

These results are qualitatively consistent with those in Fig.4b,whereascan be in principle be detected by measuring the overall propagation of the condensate along the direction of the spin-orbit coupling.

5 Conclusions

We show that the non-Hermitian skin effect emerges in a condensate of cold atoms under synthetic spin-orbit coupling and laser-induced atom loss.The non-Hermitian skin effect can be dynamically detected through the directional propagation of wavefunctions in the bulk,as well as the dynamic accumulation of atoms near the edge of the harmonic trapping potential.We also demonstrate that the mean-field interaction can have a detectable impact on the directional propagation,offering an experimentally relevant example wherein the interplay of interaction and non-Hermiticity can be directly probed.For future studies,it would be interesting to examine the manifestation of non-Hermitian skin effects in a Fermi gas.The experiment of Ref.[36] has indeed laid the foundation for such studies.In the experiment,chiral spin transfer was observed in a dissipative Fermi gas,when the atoms were manipulated to encircle an exceptional point embedded in the momentum space.As the non-Hermitian Hamiltonian implemented therein is essentially the same as that studied here,one would expect the non-Hermitian skin effect to emerge in the same experimental setup as well.In principle,the signals discussed here can in principle be measured by probing thein situdensity evolution within the trapping potential.Whether the interplay of Fermi-Dirac statistics and the non-Hermitian skin effect would bring more exotic dynamic behavior is an interesting open question which we leave to future studies.

Acknowledgements

This work was supported by the National Key Research and Development Program of China (2018YFA0307600,2017YFA0304100),the National Natural Science Foundation of China (11974331,12074419),and the Strategic Priority Research Program of Chinese Academy of Sciences(XDB33000000).

Conflict of interest

The authors declare that they have no conflict of interest.

Biographies

Haowei Liis a graduate student at the University of Science and Technology of China. His research focuses on quantum simulation and ultracold atoms.

Xiaoling Cuiis a Professor at the Institute of Physics,Chinese Academy of Sciences.She received her Ph.D.degree from the same institute in 2010.Her research interests include the few-and many-body physics of cold atomic gases,including effective scattering theory,universal bound states,polaron physics,low-dimensional systems,synthetic gauge fields,and quantum droplets.

Wei Yiis a Professor at the University of Science and Technology of China.He received his Ph.D.degree in Physics from the University of Michigan in 2007.His primary research interests include ultracold atoms,quantum simulation,and strongly correlated systems.