改进MBCV法在滚动轴承故障诊断中的应用

吴 超，崔玲丽，张建宇，王 鑫

（北京工业大学材料与制造学部，北京 100124）

引 言

滚动轴承是旋转机械设备中的关键零件，其运行状态直接影响到整个机械系统的性能。然而，由于机械设备结构复杂，工况多变，滚动轴承容易出现擦伤、裂纹、点蚀、脱落等局部损伤。据有关资料统计，在机械设备中大约有21%的故障是由轴承损伤引起。因此，为了提高滚动轴承的可靠性，保证机械设备安全运行，研究有效的轴承故障诊断方法非常必要［1⁃4］。

振动分析法由于其测量简单，蕴含信息丰富，且对滚动轴承早期故障比较敏感，被广泛应用于滚动轴承状态监测与故障诊断中［5］。当轴承表面出现损伤时，损伤点在运行过程中与其他元件产生接触冲击，该冲击由于作用时间短，频域覆盖面大，必然会激发轴承系统的固有振动频率从而产生共振，导致振动信号的幅值和频率出现调制现象［6⁃7］。同时，在工程实际中，机械系统中往往还含有其他干扰振动以及大量噪声，且故障振动信号在经过复杂的传递路径后亦会产生一定的能量衰减，导致滚动轴承的故障特征被掩盖。因此，轴承故障诊断的一个关键是实现信号分离，即从采集的振动信号中分离出轴承故障信号。目前，已有多种信号分离技术被成功用于滚动轴承故障诊断中。

Randall 等［8］提出了一种基于倒频谱编辑的故障滚动轴承振动信号与齿轮振动信号分离方法，该方法通过人工选取齿轮信号对应的倒频谱谱线进行编辑，能够有效去除目标离散频率成分，分离出滚动轴承振动信号。李红贤等［9］提出了一种迭代广义解调的变转速滚动轴承故障诊断方法。该方法消除了变转速工作模式下齿轮啮合对轴承信号干扰的问题，成功提取出了轴承故障信息，实现轴承运行状态的判断。张文义等［10］利用信号共振稀疏分解和能量算子解调相结合的方法，将信号分解为高、低共振分量，实现齿轮箱轴承故障信号的分离与诊断。

这些方法均能实现轴承故障信号的分离，但是仍存在一定的局限，不容易实现工程上的自动监测与诊断。为了实现工程上轴承的自动监测与诊断，美国学者Jacek Dybala 提出了一种自动的轴承故障诊断方法［11］。Dybala 将图像分割的经典算法——最大类间方差法引入到轴承故障信号的信号分离中。这种算法能够快速将信号频域分为上下两个类间方差最大的区间，且通过保留轴承故障信号所在的区间实现信号分离。该方法计算速度快，自适应性强，对于频谱有明显峰值差异的信号分离效果较好，但对于频谱复杂的信号效果不佳，且存在经验性选择分离次数的问题。研究发现出现这一问题的主要原因是由于MBCV 法求得的分割阈值对轴承故障信号的适应性较差。

针对这一问题，提出一种基于改进MBCV 法的滚动轴承故障诊断方法。该方法的关键在于增强分割阈值的细节表达能力，提高分离效果。首先将信号频谱均分为若干个子区间，分别求出每个子区间的MBCV 阈值，并将这些阈值进行插值拟合，从而得到整个频域的阈值曲线；调整频谱分割段数并以分离信号与原信号之间的均方根误差最小化为目标寻找最优阈值曲线；然后依据最优阈值曲线分离出轴承故障信号，并使用平方包络谱提取故障特征。试验和仿真结果表明，该方法能有效剔除强干扰成分，对轴承故障信号的分离结果更加精确，诊断结果准确率更高。

1 MBCV 算法原理

1.1 MBCV 算法原理

最大类间方差法由日本学者N Otsu 提出，用于自动计算图像阈值，对灰度图像进行二值化处理［12］。该方法将灰度图像按照灰度不同分为目标与背景两部分，通过计算目标与背景之间的类间方差并以类间方差最大时对应的灰度值作为图像二值化的标准。对于给定图像，假设总像素数为N=n0+n1+…+nL-1，灰度范围为［0，L-1］，则：

式中ni为第i个灰度等级的像素数；pi为像素点出现的概率，pi=ni/N，i=0，1，…，L-1，L为灰度等级。

区间［0，L-1］内任意灰度值k，可以将图像分为目标c0和背景c1两部分，分别由灰度值在［0，k］和［k+1，L-1］中的像素构成，c0和c1各部分的灰度均值为：

式中ω0和ω1分别为c0和c1两部分出现的概率，

整个图像的灰度均值表示为：

下式为c0和c1两部分的类间方差计算公式：

在［0，L-1］区间内，任意一个k值均对应一个类间方差。依据类间方差越大，分类效果越好的原则，确定类间方差最大时对应的k值作为最佳分割阈值。

美国学者Jacek Dybala 将MBCV 方法应用在轴承振动信号的信号分离中。他将图像各像素的灰度等级对应为信号的频谱分量的频率，每个灰度级出现的次数即像素数对应为信号谱分量的振幅，并将公式（5）等效至信号频谱中，得到频谱中类间方差计算公式：

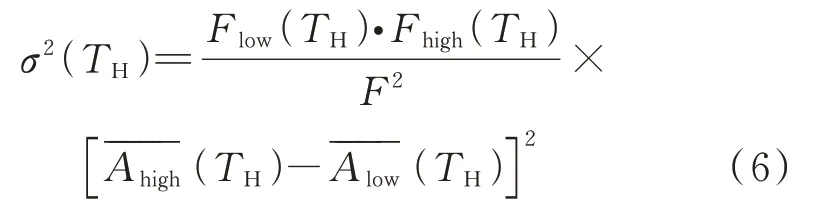
式中F为信号的所有谱频率分量的数量，Flow(TH) 为低幅值信号频谱分量的个数，Fhigh(TH)为高幅值信号频谱分量的个数，(TH)表示低振幅信号频谱分量的平均振幅(TH)表示高振幅信号频谱分量的平均振幅。

公式（6）可以自适应地求出信号频域的最优分割阈值TH。使用该阈值实现信号分离的具体流程如图1所示。

图1 基于MBCV 法的信号分离流程Fig.1 Signal separation process based on MBCV method

即先根据阈值TH将原信号频谱分为高幅值区Xhigh(f)，低幅值区Xlow(f)，再通过傅里叶逆变换将Xlow(f)转为时域信号xlow(t)。

在实际工作环境中，通过振动传感器采集的信号中含有一些齿轮啮合和系统共振分量，这些分量的能量相对于轴承故障分量要高。因此，轴承故障信息大都存在于低幅值部分中。所以，这里对低幅值信号频谱进行逆傅里叶变换得到的信号即为轴承故障信号。

1.2 仿真信号验证

通过轴承外圈故障仿真信号进一步说明MB⁃CV 法对振动信号的分类效果。为了模拟轴承的工作环境，在仿真信号中加入两个正弦信号，该信号如图2所示。

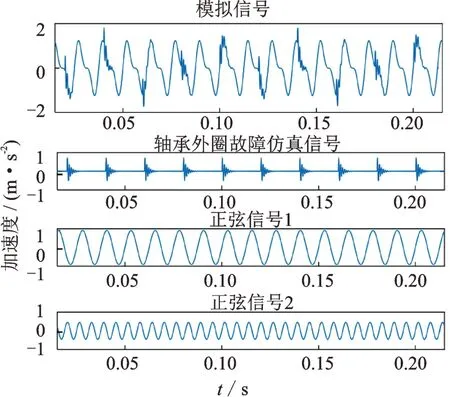
图2 模拟信号及其组成Fig.2 Simulation signal and its composition

通过公式（6），利用MBCV 法求出该模拟信号频域的阈值TH，如图3所示。

图3 传统MBCV 法的分割阈值Fig.3 Segmentation threshold of traditional MBCV method

阈值TH将整个频域分为高低两部分，分别将这两部分做逆傅里叶变换实现信号分离，分离结果如图4所示。

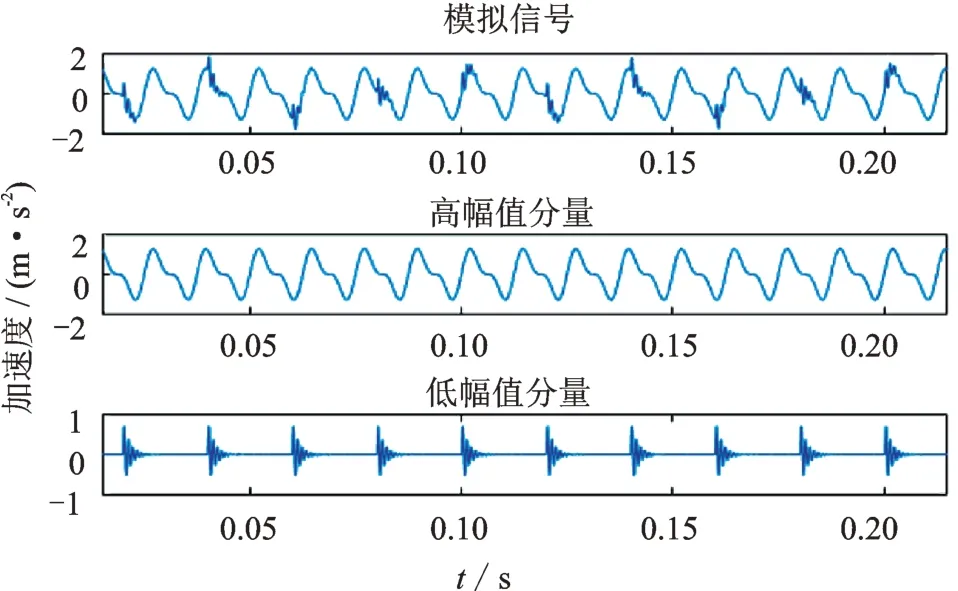
图4 模拟信号分解结果Fig.4 Simulation signal decomposition results

从图中可以看出，MBCV 法成功地从模拟信号中分离出轴承外圈故障信号。然而，对于工程实际信号来说，由于信号的组成和峰值情况未知，往往需要重复多次上述步骤才能分离出故障信号。而且，由于分离次数无法预测，需要耗费大量人力进行调试，效率低而且不够准确。为了解决这一问题，提出一种基于改进MBCV 法的滚动轴承故障诊断方法。

2 基于改进MBCV 算法的轴承故障诊断方法

2.1 改进MBCV 阈值

针对传统MBCV 法对工程实际信号的诊断效果较差甚至失效这一问题，进行了深入的研究。传统MBCV 法能实现信号分离的关键在于最大类间方差阈值的分类效果。由最大类间方差的定义可知，该阈值是一种针对整个频域的统计学阈值，而且是定值。然而，轴承故障信号的故障信息通常集中在某一频段中，这种针对整个频域的阈值无法准确提取出轴承故障信息。因此，要想达到最优的分离效果就要使阈值能在保留轴承故障信息的同时，最大程度地去除离散频率成分。

为了实现这一目标，本文对MBCV 法的阈值确定方法进行了改进。主要思路是将原来的全局阈值改为局部动态的阈值曲线，增强阈值的细节分辨能力，从而提高信号分离的准确率。具体步骤如图5所示。

图5 阈值改进步骤Fig.5 Improved threshold steps

即先将信号频谱均分为i（i>1）段，分别计算每段频域内的最大类间方差阈值，最后使用多项式插值法对所有阈值进行拟合，以拟合的阈值曲线代替原来的固定阈值。

2.2 确定最优阈值曲线

阈值曲线相较于传统的固定阈值对轴承故障信号的分离更加准确，更适合实际的轴承信号提取。但是，要想达到最优的分离效果就要使阈值曲线能在保留轴承故障信息的同时，最大程度地去除离散频率成分。对于实际采集的信号，由于其构成成分复杂、各成分峰值情况未知，无法直接确定最优阈值曲线。因此，有必要对最优阈值曲线的确定方法做进一步研究。

均方根误差能用来衡量预测值同真值之间的偏差。在轴承故障诊断中，可以通过计算最后的分离信号与原轴承故障信号之间的均方根误差来判断分离信号是否准确。均方根误差越小说明信号分离越准确。基于这一事实，提出了挑选最佳阈值曲线即确定分割段数i的方法，具体流程如下：

（a）求出信号x(t)频谱X(f)，并设置最大分割段数S，将X(f)均分为i段（i=2，3，4，…，S）；

（b）当i=2 时，根据改进的MBCV 算法分离出低振幅信号xi(t)，并求出该分量与原轴承故障信号的均方根误差RMSE；

（c）令i=i+1，返回步骤（b），开始新一轮计算，直至i>S时结束；

（d）对均方根误差数据集进行趋势拟合，均方根误差最小时对应的分割段数i最优，即此时的阈值曲线最佳。

2.3 诊断流程

在上述研究的基础上，提出了基于改进MBCV算法的轴承故障诊断流程，流程图如图6所示。

图6 改进MBCV 法的轴承故障诊断流程Fig.6 Bearing fault diagnosis flow based on improved MBCV method

3 实验验证

3.1 案例1

采用美国辛辛那提大学实验中心在2003～2004年进行的轴承寿命实验数据进行研究，实验装置如图7所示。电动机转速保持在2000 r/min，通过传送带和轴连接，轴上安装了四个Rexnord ZA⁃2115 滚动轴承，轴承每排有16 个滚子，节距直径2.815 in，滚子直径0.331 in，接触角15.17°，轴和轴承承受6000 lb（约26690 N）的径向载荷。在轴承座上安装了PCB 353B33 高灵敏度石英加速度计，采样频率20 kHz，每隔10 min 采集一次，直至轴承1 外圈出现严重损伤停机。本文只使用了在第一轴承壳体上采集到的振动信号，利用轴转频率和轴承几何形状计算了滚动轴承的特性缺陷频率。这些频率值如下：滚动体故障特征频率fBSF=139.92 Hz，保持架故障特征频率fBFF= 279.84 Hz，外圈故障特征频率fBPFO=236.40 Hz，内圈故障特征频率fBPFI=296.93 Hz。

图7 辛辛那提大学轴承实验台系统Fig.7 The bearing experimental platform system of Univer⁃sity of Cincinnati

由于该数据是在实验台上采集的，为了模拟实际工作环境，在每个轴承信号中都加入正常运行模拟变速箱信号，该信号由下式产生：

式中fz为电机转轴的转频，fk为齿轮转频，s为齿轮啮合频率的谐波倍频，Aj为第j个齿轮啮合谐波的幅值，Mzj为第j阶与轴频相关的幅值调制系数，Mkj为第j阶与齿轮转频相关的幅值调制系数，fhi为第j阶齿轮啮合谐波频率，mzj为第j阶与轴频相关的相位调制系数，mkj为第j阶与齿轮转频相关的相位调制系数，φj为第j阶相位角，n（t）为符合高斯分布的随机噪声，w为噪声幅值系数。

具体参数见文献［11］，该实验信号如图8所示。

图8 齿轮箱轴承故障信号时域图Fig.8 Time domain diagram of gearbox bearing fault signal

依据本文提出的诊断方法，对该信号进行处理。首先，预设频域最大分割段数S=32；然后，分别求出各分割段数情况下低幅值分量与轴承故障信号的均方根误差，并绘制离散图；最后，对该离散图进行多项式拟合并观察趋势，结果如图9所示。

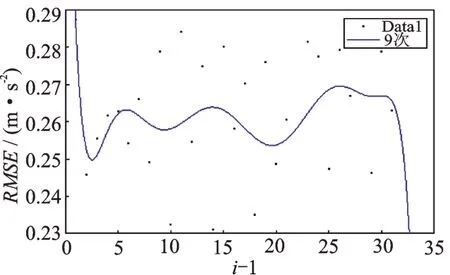
图9 均方根误差散点图及其趋势Fig.9 Root mean square error scatter plot and its trend

由图9可知，在排除末尾项后，当i=4 时，均方根误差出现首个极小值且为最小值。因此认为将频谱分为四段时求得的阈值拟合曲线能最大程度地分离出故障信号。

此时，其最优阈值拟合曲线结果如图10 所示。将阈值曲线与原方法得到的阈值进行对比，不难发现改进后的方法对轴承信息的提取效果更好。

图10 改进方法的阈值曲线和传统方法的固定阈值Fig.10 Improved threshold curve and traditional fixed threshold

求出此时对应的低幅值信号x4(t)，直接对x4(t)进行平方包络分析，包络谱如图11 所示。从图中可以清晰地诊断出轴承故障频率。同时，为了验证该方法的优越性，将其与原方法的结果进行对比。对比发现，改进后的方法要比原方法的分离效果更好，诊断结果更加准确。

图11 诊断结果Fig.11 Diagnosis results

3.2 案例2

采用美国凯斯西储大学轴承内圈故障数据进行验证。实验系统如图12 所示，左侧为一个1.5 kW的电动机，右侧为一个功率测试计。轴承型号为SKF6205，轴转速为1750 r/min，采样频率为12 kHz，损伤直径为0.028 in。为了充分验证改进方法的优越性，在采集的轴承故障信号中加入信噪比为10 的白噪声，该信号如图13 所示。

图12 凯斯西储大学实验台系统Fig.12 The bearing experimental platform system of Case Western Reserve University

图13 轴承内圈故障信号Fig.13 Bearing inner race fault signal

使用改进MBCV 法对该轴承故障信号进行分析。同样，预设最大分解段数S=32，绘制出均方根误差散点图和趋势图，如图14 所示。

由图14 可知，当i=12 时，均方根误差首次由下降变得平稳，此时获得的阈值拟合曲线最佳，该最优阈值曲线如图15 所示。

图14 均方根误差散点图及其趋势Fig.14 Root mean square error scatter plot and its trend

图15 改进方法的阈值曲线和传统方法的固定阈值Fig.15 Improved threshold curve and traditional fixed threshold

图中红色虚线为传统MBCV 方法计算出的固定阈值。分别使用改进方法和传统方法对此信号进行处理，结果如图16 所示。由图16 表明，相比原方法改进方法的诊断结果更加清晰准确。

图16 诊断结果Fig.16 Diagnosis results

4 结 论

（1）本文针对传统MBCV 方法的不足，提出了一种基于改进MBCV 法的轴承信号分离方法。该方法使用动态阈值拟合曲线代替传统的固定阈值。实验结果表明，阈值曲线增强了局部分辨率，提高了信号分离的准确率。

（2）将改进的MBCV 法应用于轴承故障诊断中。同时，根据轴承故障信号的特点提出了选取最优阈值曲线的方法。通过仿真及实验分析验证了该方法的有效性。由于该方法基本不需要人为设定参数，比较适合于工业上的自动检测系统，具有较强的实用价值。