覆盖增强主动约束层阻尼的旋转轴向FGM梁的热抑振研究

方 园，郭永彬，黎 亮，章定国

（南京理工大学理学院，江苏南京 210094）

引 言

日本学者Koizumi［1］于1987年首先提出FGM的概念，与多层纤维增强复合材料相比，FGM 制成的结构在一个表面上具有平滑、连续的特性变化的特点，消除了不连续的应力和位移分布的影响。FGM 是为了适应高温暴露条件所设计的，因此在航空航天领域被广泛应用。仝国军等［2］研究了非均匀温度场下变物性二维功能梯度材料板的瞬态热应力分布问题。Wattanasakulpon 等［3］研究了FGM 制成的弹性端约束梁的线性和非线性振动问题。Tong 等［4］研究了热磁耦合作用下悬臂FGM 纳米管的稳定性。Li 等［5］考虑了材料特性沿轴向梯度分布旋转楔形FGM 梁的刚柔耦合动力学特性。

蔡国平等［6］对中心刚体⁃柔性悬臂梁系统的动力特性进行了研究。关于柔性空间组件的结构振动控制已经有大量的研究。常用的振动控制方法包括被动控制、主动控制和主动⁃被动混合控制。覆盖有普通约束层和黏弹性材料制成阻尼层的结构称为被动约束层阻尼结构，结构振动时，通过黏弹性材料（Viscoelastic Material，VEM）的剪切变形引起的能量耗散实现振动抑制［7］。被动控制具有成本低，结构简单，可靠性高的特点，在振动的高频段具有良好的阻尼性能，但其缺乏控制的灵活性，并且结构阻尼的增加受到限制。压电材料作为一种智能材料，可以同时用作传感器和执行器。为了实现智能减振，设计了覆盖有压电层的主动抑振结构。Ghasemi⁃Nejhad 等［8］提出了带有嵌入式压电传感器和执行器的有源复合梁，这种主动控制具有更大的灵活性，并且在低振动频带中具有更好的控制效果。但是在应用压电智能结构时需要消耗外部能量，而且控制系统的设计取决于柔性机械臂的动态模型的精确性，因此纯被动控制或主动控制的使用可能无法满足工程应用的需求。结合两种方法优点的主⁃被动混合控制将是首选，该方法将被动约束层阻尼结构顶层的普通约束层替换为有源压电层来实现主被动混合约束装置的概念［9］。Li⁃ao 等［10］研究了VEM 参数如何影响主被动混合约束装置中的被动阻尼能力和主动作用。Hau 等［11］使用有限元方法对部分覆盖主被动混合约束梁进行建模。Vasques 等［12］讨论了反馈和正位反馈控制器单独使用时的缺点以及混合控制器的优点。Ku⁃mar 等［13⁃14］使用边端元来解决黏弹性层在一定程度上降低主动控制传递速率的问题。Li 等［15］在传统增强型主被动混合约束（Enhanced Active Con⁃strained Layer Damping，EACLD）梁模型的基础上，提出了一种带有部分覆盖EACLD 的旋转梁的动力学模型。Baz 等［16］开展了基于主动约束层阻尼技术的旋转梁振动抑制的实验研究，搭建了可旋转的实验平台，将ACLD 梁与测量系统和控制系统置于旋转平台，通过集电环将信号传输至计算机，实现了压电主动约束层的传感和作动功能。

本文建立了具有温度依赖性的EACLD 夹层FGM 梁的刚柔耦合动力模型，并考虑FGM 材料特性沿轴向梯度分布。与主要讨论智能复合结构的温度影响振动特性的文献研究不同［14，17⁃18］，本文将重点讨论不同参数（贴片位置、覆盖率、旋转半径以及模型的宽度）对温度场中含EACLD 贴片的旋转FGM梁动力响应的影响。

1 几何建模

1.1 基本假设

设压电约束层的厚度为h1，长度为lc，密度为ρ1，弹性模量为E1，横截面积为A1，惯性矩为I1；黏弹性材料层厚度为h2，密度为ρ2，弹性模量为E2，横截面积为A2，惯性矩为I2；基梁层的厚度为h3，长度为l，宽度为b，横截面积为A3，惯性矩为I3；R为刚性轮毂的半径，轮毂由外部扭矩驱动绕y轴旋转，其旋转惯量为Jh；keq和mp分别表示边端元体的质量和刚度。其余参数随温度变化的情况在下文有说明。在后面的推导过程中，下标1，2，3 分别表示与压电层、黏弹性层以及基梁层相关的量。

在建模过程中，本文的复合梁满足以下几个假设：

1.功能梯度梁为欧拉⁃伯努利梁，复合梁仍旧可以看作欧拉⁃伯努利梁。

2.功能梯度梁由金属和陶瓷构成，功能梯度梁的杨氏模量以及温度膨胀系数都有温度依赖性。

3.功能梯度梁分布服从幂律定律，且材料特性沿轴向呈梯度分布。

4.施加的电压沿压电层厚度方向上极化。

5.复合梁各层轴向变形包括梁的横向变形引起的轴向收缩，并且所有子层梁的横向变形是相等的。

1.2 运动几何关系及变形场描述

含部分覆盖EACLD 的功能梯度旋转梁模型如图1所示，与传统模型的主要区别在于，其基梁是由FGM 制成的具有温度依赖性的梁，且材料特性沿轴向梯度分布。图2描述了EACLD 梁的变形关系，u1表示压电层沿x轴方向的轴向变形，u2表示黏弹性层沿x轴方向的轴向变形，u3表示基梁层沿x轴方向的轴向变形，各层的横向变形量由w来表示，θ表示梁的旋转角度。

图1 含部分覆盖EACLD 的功能梯度旋转梁模型示意图Fig.1 Schematic diagram of functionally graded rotating beam model with partial coverage EACLD

图2 EACLD 梁的变形关系Fig.2 Deformation relationship of EACLD beam

uA和uB表示VEM 层上表面和下表面距z轴的距离，VEM 层绕y轴的旋转角度，其中：

其中：

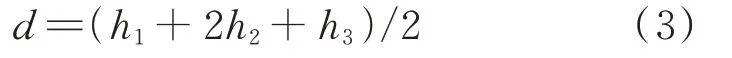
黏弹性层的轴向变形量可以表示为：

其中：

平面坐标系o⁃xz中复合梁上任意点的位置矢量可以表示为：

式中wi表示复合梁各层沿中性层方向的轴向变形量；wc表示由梁的横向弯曲引起的轴向缩短变形量，可以写为二阶耦合项［17］：

根据假设模态法，第i层沿中性轴方向的轴向变形和横向变形可以表示为：

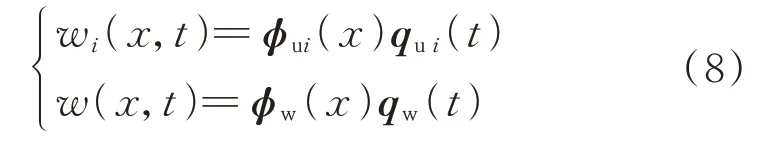
式中ϕui(x)和ϕw(x)分别为与梁的轴向和横向振动有关的模态函数；qui(t) (i=1，3)和qw(t)为结构的广义坐标。结构各层沿x方向的轴向变形可以表示为：

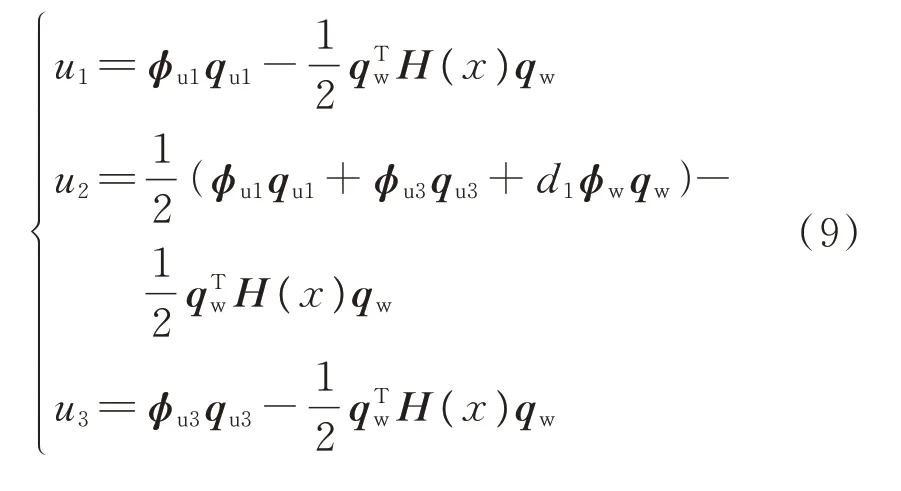
其中：

设x1和x2分别为左边端元和右边端元距基梁左端的距离：

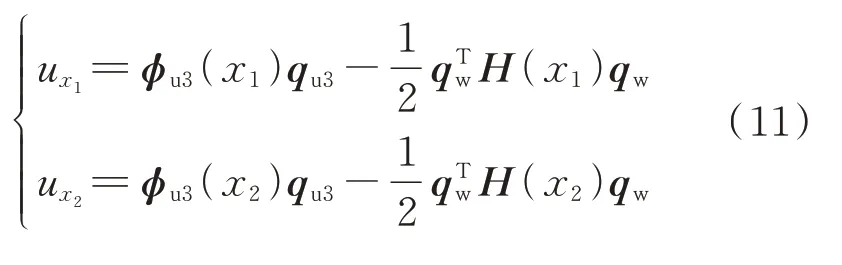
1.3 功能梯度材料概述

FGM 梁的材料特性根据幂律定律可表示为：

式中x为FGM 梁沿轴向的坐标；P(x)表示功能梯度梁材料特性沿轴向的变化情况，可以用杨氏模量E3(x)、密度ρ3(x)、热传导率K3(x)以及热膨胀系数α3(x)来代替。下标c 和m 分别表示陶瓷和金属材料；Vc代表陶瓷的体积分数；N表示体积分数指数。陶瓷的体积分数随无量纲长度变化的情况如图3所示。

图3 体积分数随无量纲长度变化的情况Fig.3 The volume fraction varies with the dimensionless length

假定温度传导仅发生在复合梁的长度方向，那么复合层沿长度方向的温度分布情况可以通过求解一维稳态热传导方程得到：

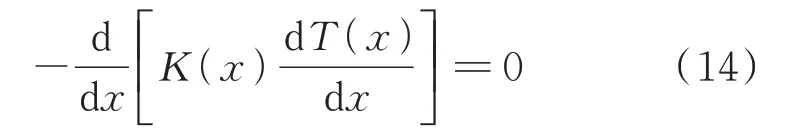
根据温度连续性和边界条件（12）～（14），可以得出以下方程式［18］：

其中：

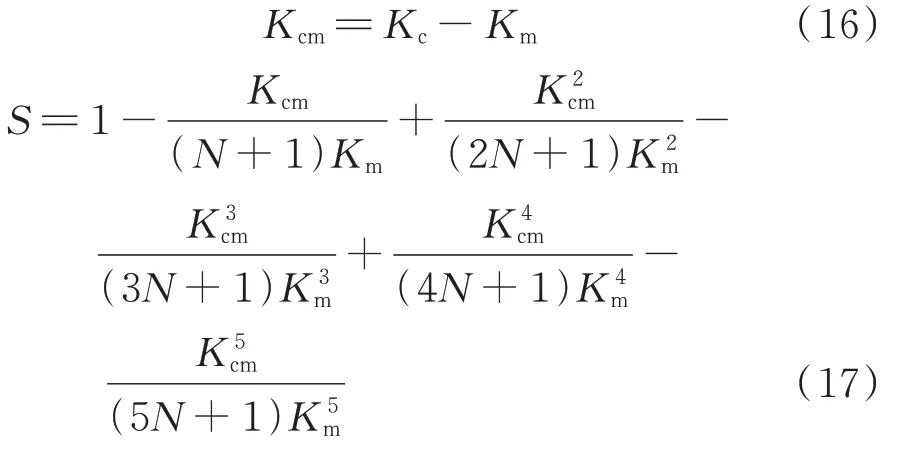
FGM 材料的杨氏模量E3(x)和温度膨胀系数α3(x)等参数的温度依赖性可以表示为［18］：

式中P0，P-1，P1，P2和P3为描述材料特性的相关系数。

黏弹性材料也具有温度依赖性，本文选用的黏弹性材料为DYAD606，其剪切模量和损耗因子随温度的变化情况与文献［17］一致。

2 系统动力学方程

对于绕定轴转动的EACLD 柔性悬臂梁，其动能可以表示为：

式中Joh为中心刚体的转动惯量。

其应变可以表示为：

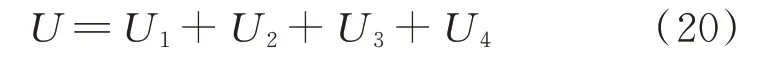
式中U1，U2，U3以及U4分别表示压电层、黏弹性层、基梁层以及等效弹簧的势能。由压电材料的一维本构方程，压电层的势能可表示为：

黏弹性层的剪切应变能可表示为：

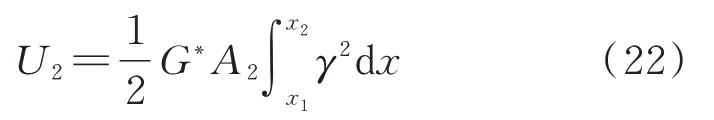
基梁层的势能可表示为：

等效弹簧的等效势能为：

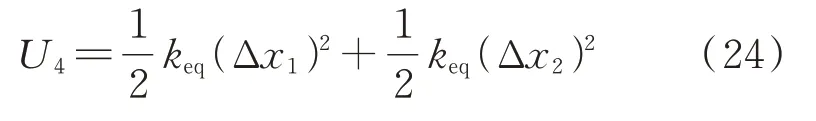
对于闭环系统，压电层在外加电场的作用下可产生压电力以及力矩。其中压电力和压电力矩所做功可以表示为：

式中d31表示压电应变常数；ϕc表示压电致动器电压；Kp和Kd分别为比例控制增益和微分控制增益；ϕs为传感器获得的感应电压，可以表示为：

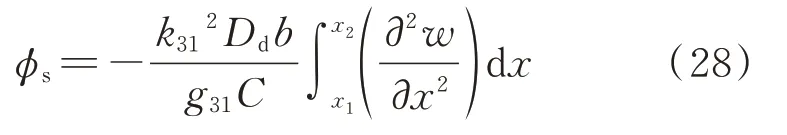
式中C=8.854×10-12Ask3th1表示传感器电容，其中，As表示传感器表面积，k3t表示介电常数；Dd=h12；k31表示力电耦合因子；g31表示压电电压常数。

与广义压电力相关的广义力可以写作：

驱动力矩所做功可表示为：

广义外力可表示为：

式中Fτ表示驱动力矩。

与温度相关的广义外力可表示为：

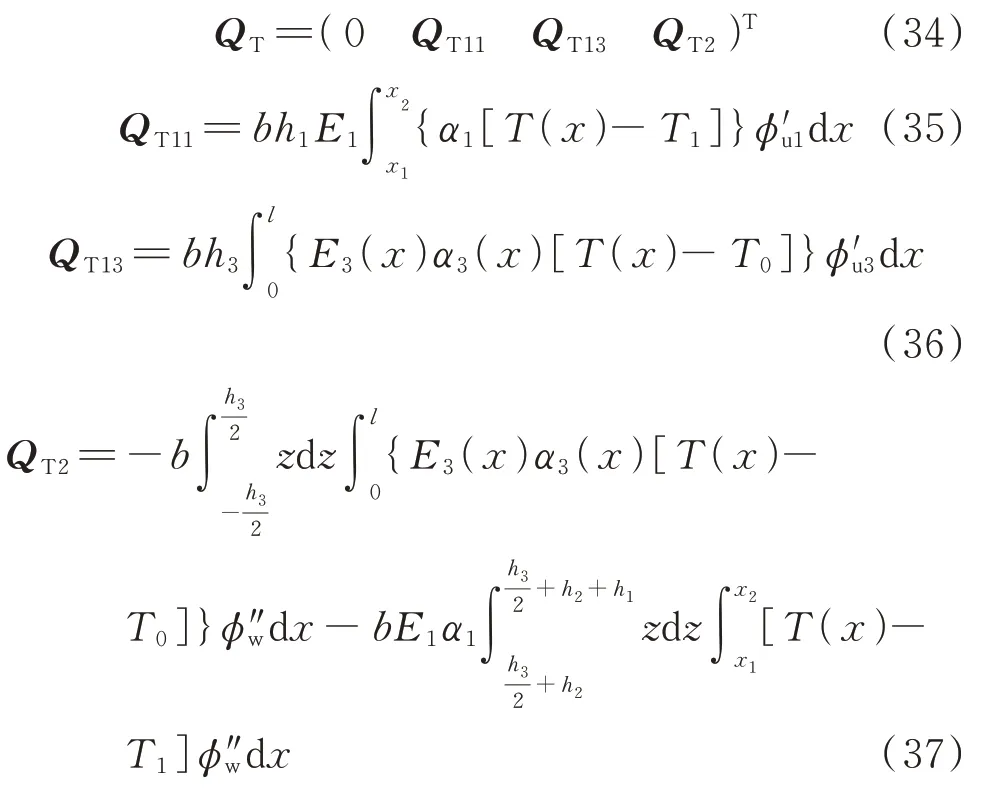
式中T1=Tx=x1；α1和α3分别表示压电层和功能梯度材料的热膨胀系数；T0为左端参考温度，T0=273.15 K。

要对系统进行响应分析，令θ，qu1，qu3以及qw为广义坐标，根据第二类拉格朗日方程：

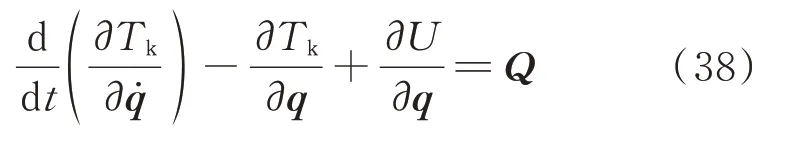
将系统的动能和势能代入拉格朗日方程，经过整理可以得到基于高阶耦合建模理论的系统动力学方程：

文献［19］中已经详细推导了材料梯度分布沿梁厚度方向变化的旋转EACLD⁃FGM 梁系统动力学模型，式（39）左边的各广义质量矩阵和右边的广义力矩阵表达形式可在文献［19］的基础上进行修改，仅需在相应矩阵元素中考虑轴向分布FGM 梁结构参数的影响，本文不再列出。

3 数值仿真结果与分析

旋转EACLD 复合梁系统的动力学特性和控制效果容易受到自身条件的影响，接下来将讨论不同控制参数对系统响应的影响。取EACLD 梁附加质量点质量为0.005 kg，等效弹簧刚度为107N m，比例控制系数Kp和微分控制系数Kd分别为1 和−0.005，在不做特殊说明的情况下默认覆盖率为1/3(x1=0.1 m，x2=x1+0.1 m)，参考温度T0=273.15 K，温度差变化范围为0～100 K。EACLD 梁的基本物理参数如表1［17］所示，FGM 材料特性随温度变化相关参数如表2［18］所示。

表1 EACLD 梁的相关物理参数表Tab.1 Relevant physical parameters of the EACLD beam

表2 金属和陶瓷材料参数随温度变化情况Tab.2 Variations of metal and ceramic material parameters with temperature

图4比较了EACLD 旋转梁在FGM 材料特性沿长度方向和厚度方向梯度分布两种情况下的热致振动情况，此时x1=0.1 m，x2=x1+0.1 m，两种梯度分布均采用相同幂律表达式。当FGM 材料特性沿梁厚度方向分布时，由于材料分布的不对称性，结构末端横向变形逐渐趋于一非零定值；而当FGM 材料特性沿梁长度方向分布时，材料分布在厚度方向具有对称性，结构末端横向变形逐渐趋于零，其振动平衡位置并未偏离梁的中性轴。

图5比较了x1=0，x2=x1+0.1 m 时，不同温度对结构末端横向变形的影响，在结构末端施加温度载荷，ΔT表示结构两端的温度差。通过对比发现，当温度差为0 K 时，经过一段时间的振动，结构末端位移逐渐趋于0，而当温度差为50 K 时，结构经过一段时间的振荡后，逐渐趋于一定值，由此可见，温度对结构振动的影响不容忽视。图6比较了x1=0.05 m，x2=x1+0.1 m 时，不同温度对结构末端横向变形的影响，得出的结果与图5相似。但当温度差为50 K 时，结构经过一段时间的振荡后，逐渐趋于一负值，而且相比下当x1=0.05 m，x2=x1+0.1 m 时结构振动的衰减速度更快。由此可见，EACLD 贴片位置靠右的结构振动控制效果相对更好。

图5 不同温度对结构末端横向变形的影响（x1=0，x2=x1+0.1 m）Fig.5 The influence of different temperatures on the trans⁃verse deformation of the structure end（x1= 0，x2=x1+0.1 m）

图6 不同温度对结构末端横向变形的影响（x1=0.05 m，x2=x1+0.1 m）Fig.6 The influence of different temperatures on the lateral deformation of the structure end（x1=0.05 m，x2=x1+0.1 m）

结构旋转半径对结构末端变形的影响如图7所示，其中图7（a）表示对横向位移的影响，图7（b）表示对轴向位移的影响。从图7中可以看出，当R=0 m 的时候结构末端变形量最小，当R=0.05 m 时结构末端变形量最大，但是旋转半径对结构末端轴向变形的影响是比较小的。

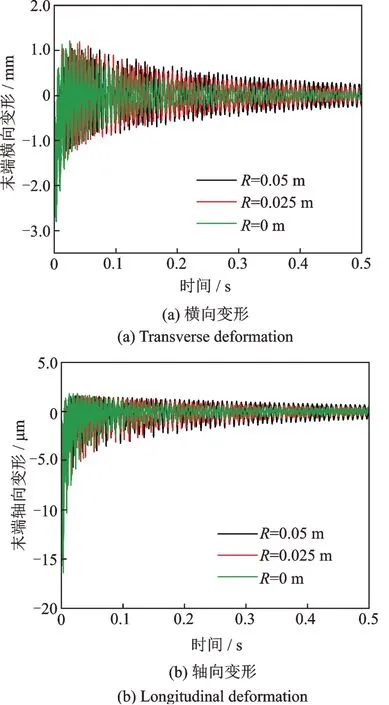
图7 旋转半径对结构末端变形的影响Fig.7 The influence of the radius of rotation on the deforma⁃tion of the structure end

图8比较了结构覆盖率对结构末端变形的影响，其中图8（a）表示对横向位移的影响，图8（b）表示对轴向位移的影响。从图8中可以得知，当结构覆盖率为1 3 时振动衰减最快，当覆盖率为3 3 时结构振幅最大且衰减速度最慢，由此可知，对结构覆盖率进行优化同样是非常有必要的。

图8 结构覆盖率对结构末端变形的影响Fig.8 The influence of structure coverage on the deforma⁃tion of structure end

图9比较了部分覆盖结构不同宽度对结构末端变形的影响，其中图9（a）表示对横向位移的影响，图9（b）表示对轴向位移的影响。从图9中可见，宽度较大时结构末端的振幅较小，因此宽度对结构的振动也是有一定影响的。图10 比较了全覆盖结构的不同宽度对结构末端变形的影响，其中图10（a）表示对横向位移的影响，图10（b）表示对轴向位移的影响。从图10 中可以看出，结构宽度对末端变形的影响非常大。对比图9和图10 发现，对于不同覆盖率的EACLD 梁，宽度对结构末端变形的影响也不相同，因此需要根据结构的实际构型对宽度进行优化，以达到有效抑振的目的。

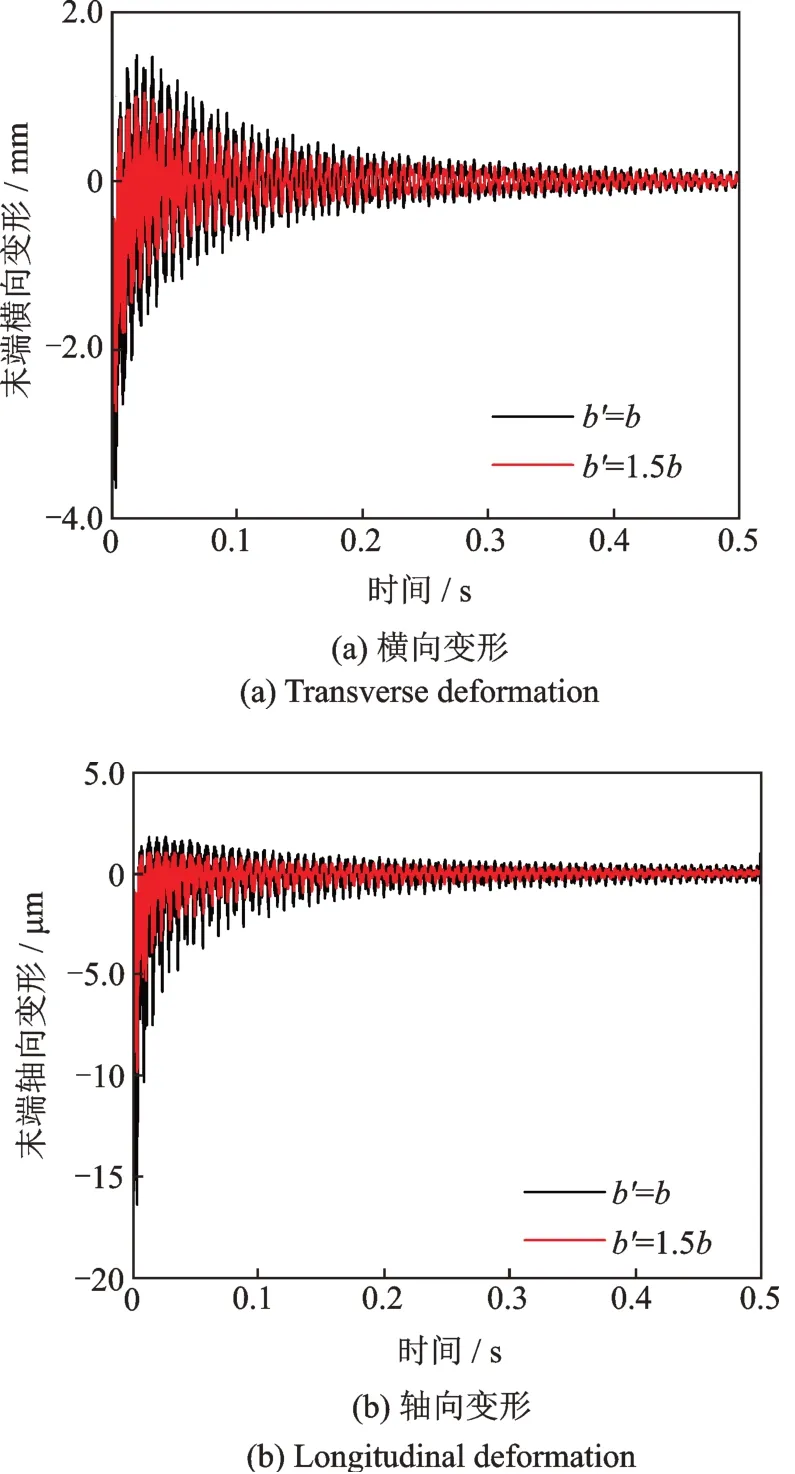
图9 不同宽度对结构末端变形的影响（部分覆盖）Fig.9 The influence of different widths on the deformation of the structure end（partial coverage）

图10 不同宽度对结构末端变形的影响（全覆盖）Fig.10 The influence of different widths on the deformation of the structure end（full coverage）

4 结 论

本文针对空间机械臂在温度场中容易发生振动的问题，以覆盖增强主动约束层阻尼的旋转FGM梁为研究对象，对简化的刚柔耦合动力学模型进行动力学建模与数值分析，得出如下结论：

（1）与材料梯度沿厚度方向按幂律分布相比，沿轴向梯度分布的FGM 梁的热致振动平衡位置不会偏离梁的中性轴。

（2）比较了贴片在不同位置/覆盖率的情况下结构振动的幅度，发现贴片位置/覆盖率对结构振动影响比较大，因此可优化贴片位置/覆盖率来减小结构振动幅度。

（3）分析了不同的旋转半径下的结构算例，发现旋转半径对结构末端轴向变形影响非常小，几乎可以忽略不计。

（4）讨论了不同宽度对结构末端变形的影响，发现宽度对结构变形影响比较大，且对于不同覆盖率的结构，宽度对变形的影响也不同，因此在进行结构设计时可对宽度进行优化。