大跨悬索桥结构阻尼的风速依赖特性研究

郭增伟，时浩博，赵 林

（1.重庆交通科研设计院有限公司桥梁工程结构动力学国家重点实验室，重庆 400067；2.重庆交通大学省部共建山区桥梁及隧道工程国家重点实验室，重庆 400074）

引 言

千米级悬索桥刚度小、阻尼低的特点致使其容易发生各种形式的风致振动，跨径排名前四的悬索桥均需要采用控制措施来克服风致振动以提高桥梁的抗风性能［1］，风荷载成为限制悬索桥跨径进一步增大的最关键的控制荷载。悬索桥加劲梁属于典型的钝体断面，空气流经加劲梁断面时会发生严重的气流分离、再附现象，并在加劲梁表面产生周期性的压力脉动，这种周期性压力脉动在影响结构振动状态的同时，也受到结构振动状态的影响，这就是桥梁风致振动区别于其他振动形式的“气动弹性”效应，气弹效应的存在将导致结构自振频率和阻尼依赖于风速［2⁃3］，因此不同风速下结构自振频率和阻尼的实测对气弹效应的研究至关重要。另外结构固有频率和阻尼也是振动控制的关键［4］，充分了解悬索桥自振频率和阻尼随风速的变化规律对悬索桥风致振动特性及其控制措施的研究有非常重要的参考价值。

目前常用的结构模态参数识别方法主要有：环境激励法和强迫振动法。环境激励法（Natural Exci⁃tation Technique，NExT）无需人工激励和大型器械、不影响结构正常使用且识别结果也相对准确，在大型结构的模态识别中应用更为广泛。1997年Pe⁃terson 等［5］首先将环境激励法引入土木工程领域，用特征系统实现算法（Eigensystem Realization Algo⁃rithm，ERA）准确识别一个4 层框架结构的自振频率，开创了环境激励法识别结构模态的先河。2006年，Huang 等［6］首先把希尔伯特⁃黄变换应用于铁路桥的健康监测中，准确识别了该桥的模态频率和模态阻尼，证明了基于环境激励的模态参数识别方法在实际工程中运用的可行性。2008年，日本东京大学Siringoringo 等［7］利用特征系统实现算法对多座桥梁进行了连续观测和参数识别，准确识别了Hakucho 桥的前5 阶模态频率，证明了环境激励法在不同种类桥梁中的普适性。2011年，姜浩等［8］利用NExT⁃ERA 方法识别了在地震激励下某座预应力混凝土连续梁桥的前4 阶竖向模态频率和模态阻尼比，发现该方法的模态频率识别结果与有限元计算结果具有良好的吻合性，模态阻尼比存在较大的误差。同年，张艳辉等［9］利用随机减量法识别出了风载激励下某刚构桥的模态频率和模态阻尼比，发现模态阻尼比的识别结果与有限元计算结果存在较大的误差，推测原因是风速对阻尼的影响。2016年，Wang 等［10］用小波变换的方法准确识别了苏通大桥在台风下的前4 阶竖向、前2 阶扭转和第1 阶水平方向的各22 组模态频率和模态阻尼比，探讨了苏通大桥的模态参数随时间的演化规律和风速对模态频率、模态阻尼比的影响，但因受到实测数据量的限制，并未论述识别结果的统计特征。2017～2018年，韩国首尔大学Kim 等［11⁃3］采用NExT⁃ERA 方法，基于Jindo 桥涡激振动实测数据系统研究了安装了多重调谐质量阻尼器后的桥梁模态和未安装阻尼器前该桥模态阻尼的变化情况，通过引入AM 函数稳定车辆荷载响应数据，并排除其他环境因素（如振动水平、温度和风速）的影响，识别出了与振幅具有线性依赖特性的阻尼比，其用95 组数据阐述了环境因素对阻尼比存在影响，但并没有对模态阻尼比在各种环境下的变化规律展开深入研究。

虽然环境激励法能较为准确地识别得到的结构自振频率，但受自然环境、车辆的影响，结构阻尼比的识别结果离散性较大；另外目前对结构自振参数的识别结果多是从确定性的角度加以描述，少有人从统计的角度考察模态阻尼随风速的变化规律。本文选取了为期一年的西堠门大桥风速和加速度响应实测数据，使用NExT⁃ERA 方法识别并分析了不同风速条件下西堠门大桥模态参数，讨论了模态阻尼比识别结果的分布规律和概型分布，最后给出了模态阻尼比随风速变化的置信区间。

1 结构模态识别NExT-ERA 方法

NExT⁃ERA 法是将自然环境激励技术和特征系统实现算法相结合的一种模态识别方法［14］。该方法首先对环境激励下结构的响应加速度数据（输出）进行预处理，并用计算得到结构的互相关函数代替脉冲响应函数，再对由脉冲响应函数构成的Hankel矩阵进行奇异值分解，得到系统的最小实现，从而得到系统矩阵，并据此求解出系统的模态频率和模态阻尼。NExT⁃ERA 方法计算效率高，对复杂的结构系统具有较强的识别能力，适用多种结构的模态识别。

用不同测点之间响应加速度的互相关函数代替传统时域模态辨识法中的自由振动响应或脉冲响应函数是NExT 方法最核心的贡献。当动力系统的k点受到单位脉冲的激励时，系统i点的脉冲响应hir（t）可表示为：

式中φir为第i测点的第r阶模态振型；akr为仅同激励点k和模态振型r有关系的常数项。

当系统k点在环境激励fk（t）作用下，系统i点和j点的响应分别是xik（t）和xjk（t），当环境激励fk（t）为白噪声时，这两者之间的互相关函数可以写为：

式中bjr为仅与参考点j及模态阶次r有关的常数项。

对比式（1）和（2）可以发现，在白噪声激励下，线性系统中任意两点的互相关函数与动力系统的脉冲响应函数除了常数项不一致外，两者函数形式完全一致，而当各测点的同阶模态振型乘以一个常数时，并不改变模态振型形状，因此用互相关函数代替脉冲响应函数的做法可用于模态参数识别中。

ERA 法的基本思想是用脉冲响应函数构造Hankel 矩阵，并对其进行奇异值分解得到系统的最小实现并求得系统矩阵A，最后求解系统矩阵A的特征值和特征向量得到系统的模态参数。广义Hankel 矩阵可以利用动态系统的脉冲响应函数h（k）进行构造［15］：

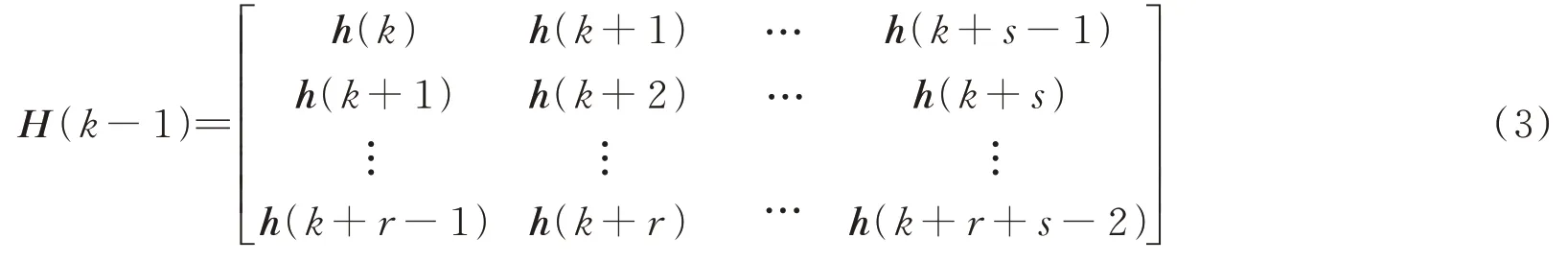
式中r=1，2，3，…；s=1，2，3，…矩阵中的每一个元素均为L×P维矩阵。

当k=1 时，对H（0）进行奇异值分解后，即可得到系统的最小实现：

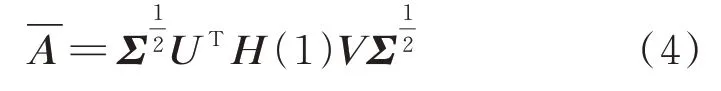
式中U，V和Σ分别为H（0）奇异值分解后的上三角、下三角和对角矩阵，而系统矩阵的特征值和特征向量即为系统的模态参数。

2 实测数据的预处理和模态识别结果准确性验证

2.1 实测结果的预处理

西堠门大桥是中国浙江省舟山市境内的跨海大桥，桥位属于典型的A 类地貌，主梁设计基准风速为55.1 m/s。桥位处风速序列利用如图1所示的安装于主跨1/4，1/2，3/4 跨径处距离桥面5 m 的灯柱上的6 个Wind Master Pro 超声风速仪收集得到（每个截面2 个风速仪），即采集的是距离海平面62.6 m处的风速；加劲梁加速度响应时间序列利用安装于主跨1/4，1/2，3/4 位置和边跨1/2 位置处的12 个加速度传感器收集得到（每个截面2 个竖向加速度计、1 个横向加速度计）；超声风速仪的采样频率为32 Hz，加速度传感器采样频率为50 Hz。

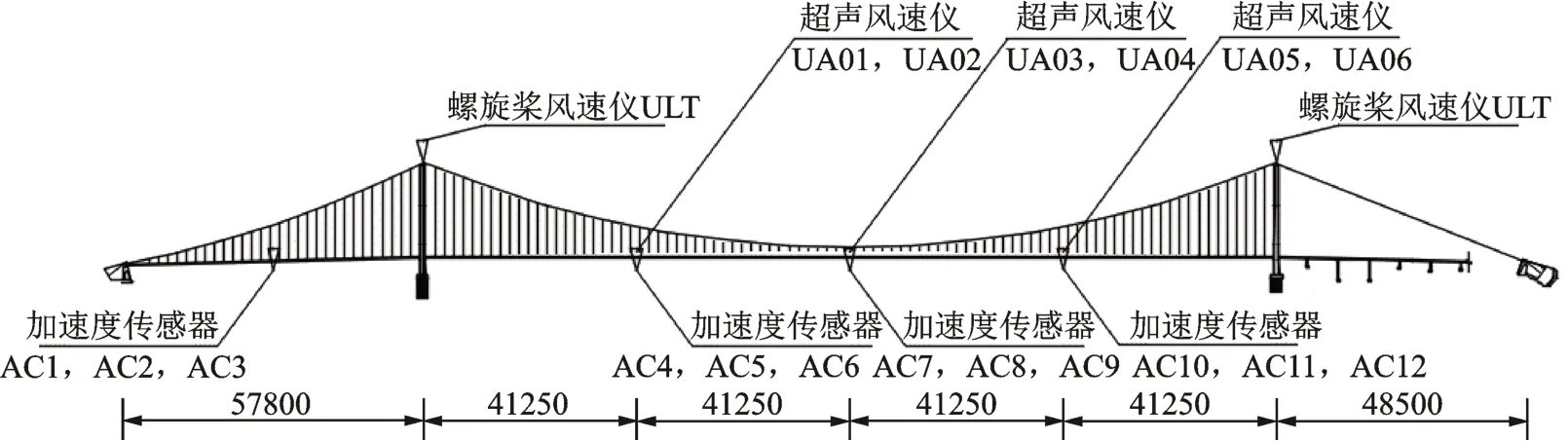
图1 西堠门大桥风速仪和加速度传感器总体布置图（单位：cm）Fig.1 Layout of the anemometers and acceleration absorbers installed on the Xihoumen Bridge（Unit：cm）

选用西堠门大桥2012年全年实测风速及响应加速度数据作为识别西堠门大桥模态的原始数据。由于风速仪和加速度计长期在潮湿环境下工作寿命缩短、在低温恶劣环境下工作易失灵、在雷暴天气下风向标易损坏、在强风天气下线路易中断等现场复杂环境的影响，上述数据中会出现一些坏点或没有数据的点，因此模态识别处理数据之前需要先剔除原始数据中一些存在明显错误的风速和加速度坏点，即采用莱茵达（PauTa）准则将实测风速和加速度时间序列中大于3 倍标准差的瞬时值予以清除［16］。另外，日常运营过程中加劲梁的加速度响应实际上是桥梁在车辆、风、温度等多种复杂动力荷载作用下的复合响应（输出）结果。因此，为尽量规避车辆、温度、风向对桥梁自振模态参数的影响，本文对实测风速与加速度数据进行了进一步的筛选。经调查发现，西堠门大桥在夜间车辆通行量远小于日间，且夜间温度相对比较稳定，故选择用于模态识别的输入与输出数据皆为从23：00 至次日早晨6：00 区段内风速与加速度数据；另外在挑选数据时段时，还限定10 min 平均风速在连续1 h 内波动不超过10%、10 min 平均风向与桥轴线方向的夹角在±60°范围内。

为了探究西堠门大桥自振频率和气动阻尼随风速的变化规律，分别从1年的监测数据中遴选了如表1所示的0，2.5，5，7.5，10，12.5 和15 m/s 七组风速条件下的共计3015 组三向加速度数据，其中每组数据都为实测夜间连续1 h 内的加速度数据，则每组内共包含25×3600=90000 个加速度数据。

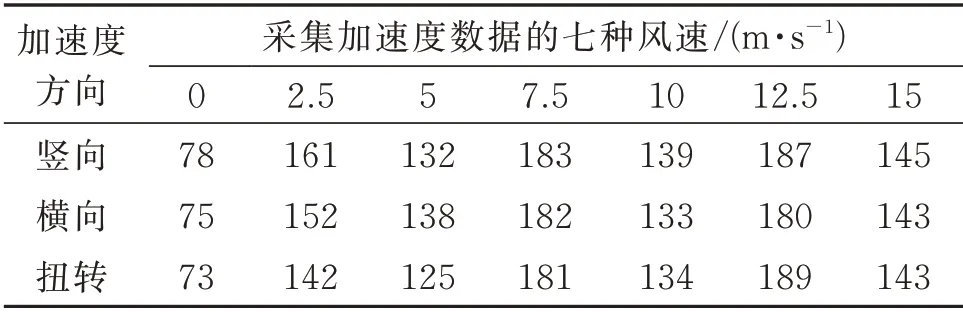
表1 七种风速条件下三向加速数据的采集组数Tab.1 Amount of acceleration samples at different wind speeds

2.2 模态识别结果的准确性验证

为验证使用NExT⁃ERA 方法识别的西堠门大桥模态结果的准确性和可靠性，选取无风环境中226 组西堠门大桥的前3 阶竖向、横向和扭转的模态频率和模态阻尼识别结果，并与ANSYS 有限元模型的计算结果以及谭庆才［17］于2012年利用强迫振动试验实测的西堠门大桥固有模态结果进行了对比，结果如表2所示。从表中可以看出，NExT⁃ERA方法识别得到的主梁竖向、横向及扭转的模态频率均值与有限元计算结果和强迫振动试验结果吻合良好，识别误差均在0.4%以内，且226 组振动样本频率识别结果的变异系数不超过0.05；虽然226 组样本的模态阻尼均值也均在现场强迫振动试验给定的范围内，但利用不同振动样本时间序列识别得到的模态阻尼波动明显，扭转阻尼的变异系数接近于1.0；横向和扭转阻尼比大致相当，但竖向振动阻尼比均值仅为横向和扭转阻尼的40%左右，在统计意义上与横向和扭转阻尼比的差异显著。总体而言，使用NExT⁃ERA 方法能较为准确、可靠地识别西堠门大桥的模态参数。

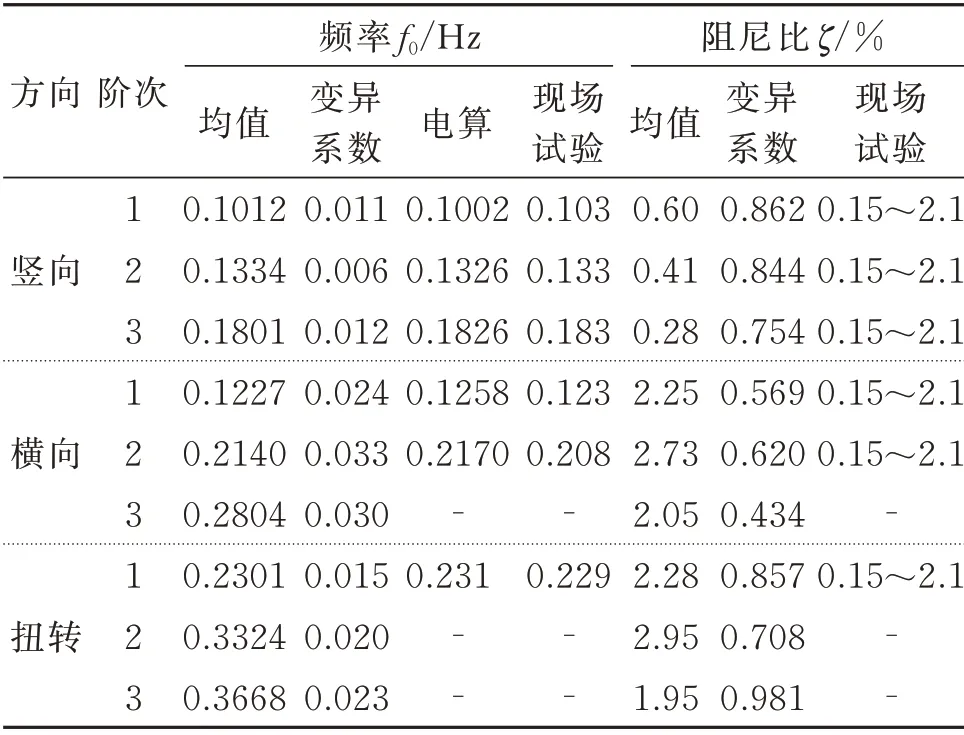
表2 模态识别结果与电算及振动试验结果的对比Tab.2 Comparison of the identification results obtained by different methods

需要特别说的是，NExT⁃ERA 模态参数方法中时间序列的总长度、采样频率和Hankel 矩阵维数的取值会影响到互相关函数的质量，经过多次尝试，最终发现用于西堠门大桥模态参数识别的样本总时长不宜小于结构基本周期的120 倍，采样频率不宜低于25 Hz，Hankel 矩阵的维数不宜低于340，权衡计算成本后，确定上述3 个参数的取值分别为：60 min，25 Hz，340。

3 模态阻尼随风速的变化规律

利用经过预处理的0，2.5，5，7.5，10，12.5 和15 m/s 七组风速条件下的共3015 组三向加速度时程样本数据进行结构模态参数识别，为形象说明不同样本序列识别结果的波动性，图2给出了平均风速为2.5 m/s 时，455 组利用主梁加速度数据识别得到的西堠门大桥竖向、横向及扭转模态频率和模态阻尼。

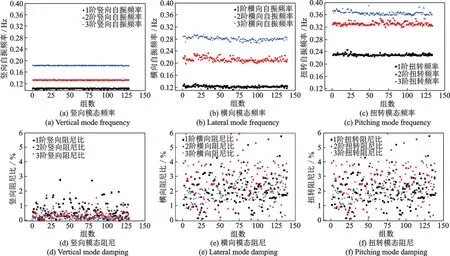
图2 风速2.5 m/s 下竖向、横向及扭转模态频率和阻尼比的识别结果Fig.2 Identification results of modal frequency and damping ratio in vertical，lateral and pitching direction at the wind speed of 2.5 m/s

从图中可以看出，NExT⁃ERA 方法具有稳定的频率识别能力，基于455 组主梁振动加速度时程序列识别得到的西堠门大桥主梁竖向、横向和扭转三个方向的前3 阶自振频率受样本序列的影响较小，相对而言竖向和扭转频率受样本影响的波动略低于横向振动频率；然而，利用不同样本序列获得的竖向、横向、扭转三个方向的阻尼识别结果则波动明显，且扭转阻尼比受振动样本时间序列的影响最大、横向阻尼比次之、竖向阻尼比最小。阻尼比受加劲梁加速度时间序列样本显著变化的现象说明从统计的角度描述结构阻尼随风速的变化规律更为科学、准确。

3.1 不同风速下三向模态阻尼识别结果

七组风速下使用不同加速度时间序列获得的结构模态阻尼均呈现出波动的特征，而气动阻尼的风速依赖特性必然造成结构模态阻尼的波动程度、范围也各不相同。为了探究结构模态阻尼的分布区间、波动程度与风速的依赖关系，图3给出了七组风速下结构竖向、横向及扭转模态阻尼随风速变化的箱型图。从图中不难看出：总体上相同风速条件下结构扭转和横向振动阻尼的均值和方差均大于竖向振动阻尼，但随着风速的增大，这种差异将逐渐减弱；从均值上看，结构竖向模态阻尼随风速的增大而增大，扭转阻尼则随风速的增大略有下降，而横向模态阻尼受风速影响不大；从离散性上看，竖向振动模态的离散程度随风速的增大而增大，扭转阻尼的离散程度随风速的增大略有下降，而横向振动模态阻尼的离散程度则基本不受风速变化的影响。

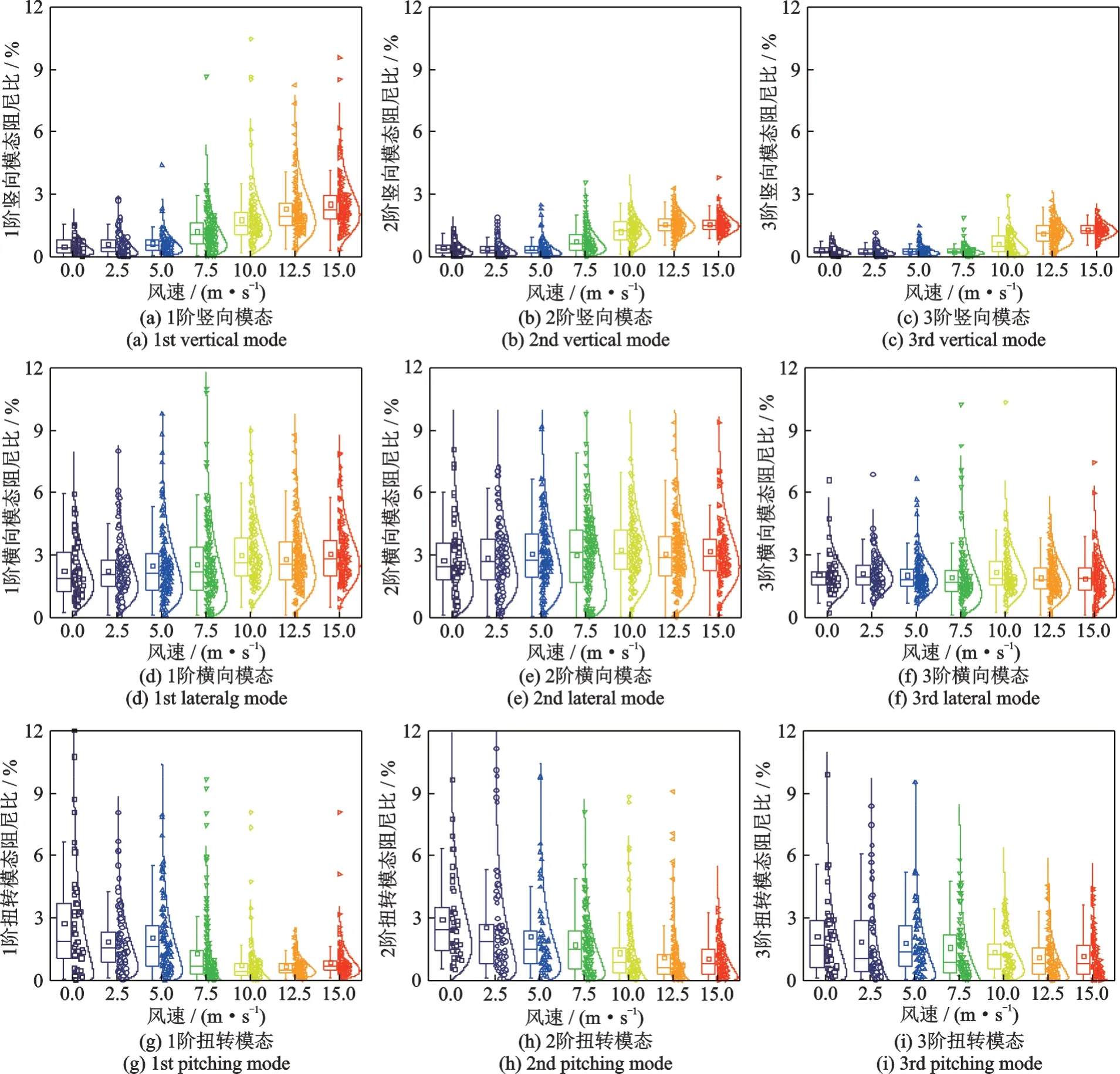
图3 竖向、横向和扭转的模态阻尼比随风速变化的箱型图Fig.3 Box diagram of modal damping ratio in vertical，lateral and pitching direction at different wind speed

大量的风洞试验和理论分析［18］表明：当气流流经桥梁断面时，空气与主梁的气动耦合产生的自激气动升力与加劲梁振动位移相位差在180°左右，产生了随风速增大而增大的正气动阻尼，正气动阻尼与结构自身阻尼叠加后将导致桥梁整体的竖向模态阻尼随风速增大而增大的现象；但是气动自激升力矩的方向与加劲梁振动位移之间相位差在0°左右，产生了随风速增大而增大的负气动阻尼，负气动阻尼与结构自身阻尼叠加后将导致桥梁整体的竖向模态阻尼随风速增大而降低的现象。本文使用NExT⁃ERA 模态识别算法得到的阻尼随风速的变化趋势与上述理论分析结果一致，证实了本文结果的正确性。

3.2 模态阻尼分布的概型分布

三个方向阻尼比的识别结果都表现出一定的随机性和离散性，随机变量的概型分布是描述其统计特性的最重要指标之一，而400 多组的加速度时间序列的识别结果也为结构阻尼比概型分布的研究提供了数据基础。

概型分布的检验方法主要有：卡方检验、蒙特卡洛法、K⁃S 检验法。K⁃S 检验法一般使用p值（原假设下观察到的检验统计量等于或大于观测值的概率）来评价样本数据分布与理论分布的相似性，进而确定随机变量的概率分布类型，p值越接近0，表示拒绝原假设的统计学依据越充分，p值越接近1，表示接受原假设的统计学依据越充分。使用K⁃S 检验法计算不同风速下各阶模态阻尼在广义极值分布假设条件下的p值，在与0.05 检验水平下观测值概率对比后，发现不同风速下各阶模态阻尼比不拒绝服从广义极值分布。

图4给出了用广义极值分布的概率密度函数（PDF）对在6 种风速条件下1 阶竖弯模态阻尼的拟合结果。从图中可以看出，广义极值分布能很好地拟合各风速下结构的竖弯模态阻尼；随着风速的增大，1 阶竖弯阻尼比的分布形状发生了从“矮胖”到“瘦高”的明显变化，到风速为12.5 m/s 时，1 阶竖弯阻尼比的分布形状最为“瘦高”，即竖弯阻尼比识别结果的离散性最小，当风速继续增大到15 m/s时，1 阶竖弯阻尼比的分布形状又变得稍“矮胖”，即此时的竖弯阻尼比识别结果的离散性又逐渐增大了。

图4 各风速下1 阶竖弯阻尼识别结果的PDF 拟合结果Fig.4 Fitting results of damping ratio of 1st vertical mode at different wind speed

广义极值分布是三种极值分布的广义函数，形状参数γ决定了极值分布的类型。当γ=0 时，广义极值分布退化为尾部呈指数下降的极值Ⅰ型分布；当γ>0 时，广义极值分布退化为尾部呈多项式下降的极值Ⅱ型分布；当γ<0 时，广义极值分布退化为尾部有限的极值Ⅲ型分布。位置参数μ反映了极值分布的均值，尺度参数σ反映了极值分布的方差。为了进一步探究不同风速下的三个方向阻尼比的概率分布，图5给出了三个方向前3 阶阻尼比广义极值分布的形状函数γ随风速的变化。从图中可以看出：总体而言，虽然扭转振型阻尼的概型分布并不随风速变化（始终为极值Ⅱ型分布），但其形状函数γ随风速的明显波动表明扭转振型阻尼的分布形状受风速影响明显；横向振型阻尼的形状参数γ随风速波动较小，表明其概型分布受风速的影响不大；竖向振型阻尼的形状参数γ随风速波动明显且发生符号改变，表明其概型分布受风速影响较大。具体而言，1 阶竖向阻尼比分布的形状参数γ均大于0，说明1阶竖向模态阻尼比均服从极值Ⅱ型分布，2 阶和3 阶竖向阻尼比分布的形状参数在低风速下大于零、而在高风速下小于零，表明2 阶和3 阶竖向阻尼比的分布在低风速下服从极值Ⅱ型分布、在高风速下服从极值III 型分布；1 阶横向模态阻尼比均服从极值Ⅱ型分布，2 阶横向阻尼比服从极值Ⅲ型分布，3 阶横向阻尼比的分布在低风速下服从极值Ⅱ型分布，在高风速下服从极值Ⅲ型分布，前3 阶扭转模态阻尼比均服从极值Ⅱ型分布。

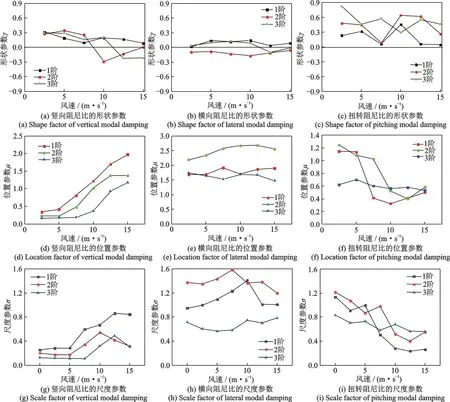
图5 模态阻尼比广义极值分布中特征参数随风速的变化Fig.5 GEV distribution parameters of mode damping ratio at different wind speed

另外，从位置参数μ（均值）和尺度参数σ（标准差）随风速的变化趋势可以看出，竖向阻尼的均值和标准差随风速的增大而增大，扭转阻尼的均值和标准差则随风速的增大而减小，而横向阻尼的均值和标准差受风速的影响并不显著。

3.3 模态阻尼随风速演化的置信区间

对不同风速条件下三个方向前3 阶结构模态阻尼的概率密度函数进行拟合，即可得到各工况下结构模态阻尼比的概型分布特征参数，据此便可获得各工况下结构模态阻尼比在不同保证率下的置信区间。图6给出了95%的置信水平下，三个方向前3阶结构模态阻尼比的置信区间随风速的变化情况。

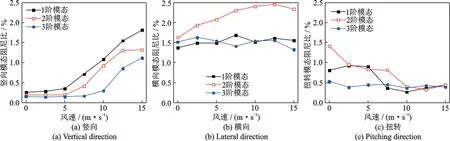
图6 不同风速下的95%置信水平的模态阻尼比下限Fig.6 Lower limit of modal damping ratio at different wind speed in 95% confidence level

总体而言，西堠门大桥的阻尼比相对较低，在95%的保证率下，前3 阶竖向阻尼比的分布区间为0.2%～2.1%，前3 阶横向阻尼比的分布区间为1.3%～2.8%，前3 阶扭转阻尼比的分布区间为0.3%～2.3%。从图6（a）中可以更为明显的看出，当风速低于7.5 m/s 时，前3 阶竖向阻尼比受风速的影响并不十分显著，但风速超过7.5 m/s 后，前3 阶竖向阻尼比将随风速的增大明显增大，且阻尼比置信区间的宽度也随风速的增大逐渐增大；3 阶竖向振型的阻尼比在风速达到10 m/s 后才随风速显著增加，这表明低阶竖向振型的阻尼比相对于高阶振型更容易受风速的影响。从图6（b）中可以明显看出，1 阶和3 阶横向阻尼比随风速增大表现出在某一平衡位置上下波动的趋势，2 阶横向阻尼比随风速增大表现为缓慢增大的趋势，但风速的变化对各阶横向阻尼比的大小及离散性的影响都较小。从图6（c）中可以明显看出，3 阶扭转阻尼随风速的增大都呈现下降趋势，且置信区间宽度逐渐变窄，与竖向振动阻尼相反，当风速低于7.5 m/s 时，各阶扭转振型阻尼受风速影响较大，而风速超过7.5 m/s 扭转阻尼受风速影响逐渐减弱，相对而言低阶扭转振型阻尼受风速的变化更为敏感。

4 结 论

以西堠门大桥的实际工程背景、基于现场采集风速和加速度数据，识别了不同风速条件下共3015组三向加速度数据对应的模态参数，重点讨论了结构模态阻尼随风速的变化规律，分析了模态阻尼比的概型分布及其置信区间，得到如下结论：

（1）西堠门大桥的三向模态参数识别结果与有限元模态分析以及现场振动试验结果相吻合，NExT⁃ERA 方法可以高效准确的识别西堠门大桥的模态参数；

（2）不同风速下西堠门大桥横向振动阻尼比均在1.0%以上，但特定风速下结构竖向和扭转振动阻尼在95%保证率的最小值分别为0.2%和0.3%，仅为设计建议值0.5%的一半，抗风设计和风洞试验时应该引起足够的重视；

（3）随着风速的增大，结构竖向振型阻尼的均值和方差总体呈上升趋势，扭转振型阻尼的均值和方差总体呈减小趋势，横向振型的均值和方差受风速的影响不大。

（4）不同风速条件下西堠门大桥三个方向的模态阻尼比不拒绝服从广义极值分布，但风速会影响结构竖向和扭转振型阻尼的概型分布的拖尾性质。