风和车流作用下悬索桥纵向减振及阻尼器参数优化
张少强,钱逸哲,朱 金,李永乐
(1.中电建路桥集团有限公司,北京 100048;2.西南交通大学桥梁工程系,四川成都 610031)
引 言
大跨桥梁结构通常采用半漂浮体系或漂浮体系,即加劲梁不设纵向约束,导致结构纵向刚度小,对风、车流、地震等外部激励引起的加劲梁纵向振动非常敏感。有研究表明,作为大跨桥梁运营阶段常见的动力荷载,风和车流荷载的长期作用会引起加劲梁梁端的反复纵向振动,由此导致过大的纵向累积位移可能会诱发梁端伸缩缝的病害,这不仅会对桥上行车的舒适性产生较大的影响,也会直接影响桥梁服役寿命与结构安全[1]。
近年来,国内外已有众多学者开展了针对大跨桥梁结构运营阶段加劲梁纵向振动特性的研究。目前,桥梁健康监测和数值仿真是分析和评估大跨桥梁加劲梁纵向振动性能两种主要的手段。桥梁健康监测方法采用已建桥梁健康监测系统中拉线式位移传感器对运营状态下的纵向变形进行实时监测、记录与分析。Ni 等[2]建立了青马大桥梁端纵向位移与温度间的数学关系模型,并在此基础之上评估了该桥梁端伸缩缝的服役表现。张宇峰等[3]基于江阴长江大桥和润扬长江大桥2 座悬索桥的梁端纵向位移健康监测数据,建立了纵向位移与有效温度间的线性相关模型,并采用梁端纵向累积位移等指标预测了梁端伸缩缝的使用寿命。邓扬等[4]基于润扬长江大桥的监测数据研究了由温度、风和交通荷载引起的梁端纵向位移变化规律,并建立了环境荷载与纵向位移间的线性相关模型。Guo 等[1,5]基于国内3 座悬索桥的长期健康监测数据,对梁端纵向位移进行了频谱分析,研究表明风和车流荷载产生的高频反复位移是导致伸缩缝损伤破坏的重要原因;同时指出在梁端增设阻尼器装置可同时降低梁端纵向位移幅值和累积位移。基于桥梁健康监测系统得到的梁端纵向位移通常包含了温度、风和运营车流荷载等的贡献,在分析单一荷载因素影响时,需要对数据进行精确剥离,处理起来较为困难;此外,通过健康监测系统获得的数据本身也受到测量精度等限制。与桥梁健康监测相比,数值模拟方法可针对多种运营阶段荷载工况进行受力和参数敏感性分析,省时、省力且易操作[6]。韩大章等[7]以集中力模拟车辆荷载,研究了随机车流荷载中车重与车速对润扬长江大桥梁端纵向位移频谱的影响,并分析了两类车流限速和增设梁端阻尼器对梁端纵向振动的减振效果;孙璋鸿[8]研究了温度、车辆激励下矮寨大桥梁端位移响应,并指出该悬索桥梁端位移与温度呈负相关,汽车荷载是引起加劲梁振动进而导致梁端大量累积位移的主要原因;李光玲等[6]研究了风和随机车流下悬索桥纵向变形,探讨了车流和风荷载对梁端纵向振动响应的影响规律,并指出风和车流荷载引起的加劲梁纵向极值小于梁端伸缩缝设计允许伸缩量,但引起的累积位移对于伸缩缝使用寿命的影响不容忽视。
前述提及的大部分研究没有系统地考虑车⁃桥或风⁃车⁃桥间的耦合作用,这主要是由于目前依托商业有限元分析软件进行风⁃车⁃桥耦合振动的分析还比较困难。此外,目前关于大跨桥梁加劲梁纵向振动的研究多侧重于加劲梁在荷载下纵向振动响应的规律,并未针对加劲梁纵向振动的控制措施做进一步深入研究。鉴于此,开展运营阶段大跨桥梁结构在风和车流作用下的纵向振动特性以及合理减振措施的研究对于保证梁端大型附属结构(如伸缩缝、阻尼器、支座等)的正常使用以及制定相应的维护养护策略具有十分重要的意义。用于桥梁主梁纵向减振的阻尼器一般可分为速度型阻尼器、位移型阻尼器以及电涡流阻尼器三类。位移型阻尼器具有非线性的特性,但这类阻尼器的非线性时程分析较为复杂,精度不易控制,所以目前针对该类阻尼器的研究较少[9]。电涡流阻尼器尚处于起步研发阶段,目前只是小规模应用于实际工程[10]。速度型阻尼器的工作特性与加载频率、加速度相关,常用的有黏滞阻尼器和黏弹性阻尼器等[11]。其中,较为成熟且适用于大跨度桥梁纵向减振的阻尼器主要是液体黏滞阻尼器。液体黏滞阻尼器由活塞、缸体和充满缸体内部的黏滞液体组成,利用活塞在黏滞液体中的运动来消耗加劲梁纵向振动时的能量。本文采用液体黏滞阻尼器作为桥梁主梁的纵向减振装置。
1 风‑车‑桥系统运动方程
本文基于已有的风⁃车⁃桥耦合振动分析系统[12],通过引入液体黏滞阻尼器单元,实现随机风和车流荷载作用下大跨桥梁结构的纵向振动及减振分析。风⁃车⁃桥耦合振动系统包含了随机车流、随机风荷载和桥梁三者之间的相互作用。本文采用元胞自动机模拟随机车流,并将车流中的每一辆车模拟成质量⁃弹簧⁃阻尼体系[13];采用有限元模型模拟桥梁结构;将路面不平顺和随机风场模拟成与空间相关的平稳随机过程。同时,将作用在桥梁上的风荷载模拟成静风力、抖振力和自激力;将作用在车辆上的风荷载模拟成静风力和抖振力;车辆与桥梁之间的相互作用通过车辆子系统和桥梁子系统之间的分离迭代来描述;液体黏滞阻尼器通常设置在塔梁之间,当加劲梁产生纵向振动时会受到阻尼器产生的阻尼力作用,从而达到纵向减振的目的。通过上述模拟,引入液体黏滞阻尼器的风⁃车⁃桥耦合振动系统的运动方程可表示为:

式中M,C,K分别表示质量矩阵、阻尼矩阵和刚度矩阵;分别表示加速度、速度和位移向量;下标b 表示桥梁子系统;下标v 表示车辆子系统(vi表示第i辆车);Fw⁃b和Fd分别表示作用于桥梁上的风荷载和阻尼力;Fw⁃vi表示作用于第i辆车的风荷载;Fvi⁃b,Fb⁃vi表示车⁃桥系统间的相互作用力。由于针对风⁃车⁃桥的研究已比较丰富[14⁃16],限于篇幅,本文仅简要介绍主梁风荷载和车辆风荷载。
作用在桥梁主梁上的风荷载通常被分成三部分,即由平均风引起的静风力、由脉动风引起的抖振力以及由结构与流体相互作用引起的自激力。
作用在单位长度主梁上的静力风荷载可表示为:

式中Lst,Dst,Mst分别为静风升力、阻力和力矩;q=0.5ρU2为气流动压,其中ρ为空气密度,U为来流平均风速;B为主梁断面宽度;CL(α),CD(α)和CM(α)分别为风轴系中的静风升力、阻力和力矩系数;α为气流攻角。
由脉动风引起的抖振力可通过Scanlan[17]提出的抖振力模型来计算:

式中Lb(t),Db(t),Mb(t)分别为单位长度主梁上的抖振升力、阻力和力矩;C′L(α),C′D(α),C′M(α)分别为静力三分力系数CL(α),CD(α),CM(α)对风攻角α的导数;u(t)和w(t)分别为横向和竖向脉动风速;t为时间。
对于由风与桥梁气动耦合产生的自激力,可通过Lin 等[18]提出的以脉冲响应函数表示的时域表达式进行计算。其表达式为:

式中Lse(t),Dse(t),Mse(t)分别为主梁单位长度上的自激升力、阻力和力矩;h,p,φ分别为主梁的竖向、横向和扭转位移;F(Crx,x,t)(r=L,D,M;x=h,p,φ)是由桥梁运动引起的9 个自激分力,其表达式为:

式中C1~C4,d3和d4分别为各自激分力对应的6 个待定系数,可通过最小二乘法拟合风洞试验获取的颤振导数得到[19]。本文算例采用的主梁断面颤振导数如图1所示。

图1 主梁断面颤振导数Fig.1 Flutter derivatives of the bridge deck
通过组集上述的静风力、抖振力和自激力,最终得到作用在主梁上的风荷载:

作用在车辆上的风荷载由平均风和脉动风产生,由于脉动风速和车辆的空间位置均具有时变性,因此,行驶在桥梁上的车辆所受的风荷载是时间和空间的函数[20]。本文参考文献[20]所提出的方法计算作用在车辆上的风荷载,简述如下:
确定作用于车辆上的合成风速和合成角度是计算车辆风荷载的前提。如图2所示,假定车速为Uv,平均风速为U,作用于车辆上的顺风向和横风向脉动风速分别为u0(xv,t)和v0(xv,t),则根据矢量合成法可以获得车辆上的合成速度Ur和合成角度ψ[20]:

图2 车辆风速合成Fig.2 Composition of velocities on vehicle

需要说明的是,由于车辆位置是时变的,作用在车辆上的脉动风速应与作用在该处桥面的脉动风速一致。假设t时刻车辆的位置xv位于桥面i节点和j节点之间,则该时刻车辆顺风向和横风向的脉动风速u0(xv,t)和v0(xv,t)分别为:

式中xi,xj分别为节点i,j的坐标;u0i(t),u0j(t),v0i(t),v0j(t)分别为桥面i节点和j节点在t时刻的顺风向和横风向脉动风速。
为了计算车辆风荷载,除了确定车辆上的合成风速以外,还需要测定车辆的气动力系数。针对本文研究的7 种典型车辆,采用风洞试验测定其气动力系数。该风洞试验在西南交通大学风工程四川省重点实验室的XNJD⁃1 风洞中进行。以2 轴货车为例,图3给出了该类型车辆的气动系数。

图3 2 轴货车气动力系数Fig.3 Aerodynamic coefficients of a 2-axle truck
车辆气动力模型Fw⁃vi={FS,FL,FD,MP,MY,MR}T可以表示为上述获得的车辆合成风速、合成角度和车辆气动力系数的函数:

式中FS,FL,FD,MP,MY,MR分别为车辆受到的侧向力、升力、阻力、俯仰力矩、偏转力矩和侧倾力矩;CS(ψ),CL(ψ),CD(ψ),CP(ψ),CY(ψ),CR(ψ)分别为侧向力系数、升力系数、阻力系数、俯仰力矩系数、偏转力矩系数和侧倾力矩系数;A为车辆阻风面积;hv为车辆质心高度。
路面粗糙度是风⁃车⁃桥耦合振动重要的激励源之一,本文通过傅里叶逆变换[21],采用Shinozuka等[22]提出的干扰谱生成路面粗糙度,功率谱密度函数为:

式中n为傅里叶逆变换中的采点数,取值为2048;n0为不连续频率,设为0.16 m-1;ϕ(n0)=8×10-5,2×10-5和5×10-6分别表示一般、好和很好的路况,本文的路面粗糙度等级设置为“很好”。
式(1)中的阻尼力由位于塔梁连接处的液体黏滞阻尼器提供,其表达式如下:

式中H为阻尼力的位置矩阵;F(t)为液体黏滞阻尼器提供的阻尼力:

式中F为液体黏滞阻尼器的阻尼力(kN);sgn(V)为符号函数,表示阻尼力的方向;C为阻尼系数(kN/(m/s)α);V为阻尼器两端相对速度,即活塞运动速度(m/s);α为速度指数,0<α≤1,当α≠1 时为非线性液体黏滞阻尼器;下标i为桥梁上设置的第i个液体黏滞阻尼器。
本文采用分离迭代方法求解风⁃车⁃桥耦合振动方程,即用分离迭代法在每一积分步分别独立求解式(1)和式(2),再根据两个子系统间的耦合关系进行平衡迭代[19],风⁃车⁃桥耦合振动分析流程如图4所示。

图4 风⁃车⁃桥耦合振动分析流程图Fig.4 The solving procedure of coupled wind-vehicle-bridge analysis
2 工程实例
2.1 桥梁概况
本文以某在建主跨为700 m 的流线型钢箱梁单跨悬索桥为工程背景,该桥是一座跨越山谷的双塔公路悬索桥,结构体系采用半漂浮体系。加劲梁宽27.9 m,高3.0 m,两侧设有风嘴,内部有U 形肋和横隔板。桥面设置成双向4 车道,设计荷载等级为公路⁃I 级,设计行车速度为80 km/h。成桥后中跨主缆矢跨比为1/10,矢度70 m。该桥的立面布置图如图5所示。

图5 钢箱梁悬索桥(单位:m)Fig.5 Steel box girder suspension bridge(Unit:m)
2.2 工况设置
根据桥址处的风速实测数据,本文选取了常遇风速(5 m/s)和极端风速(20 m/s)两种风荷载工况。此外,由于缺乏桥址处交通流的实测数据,本文在设置车流工况时参考了位于类似山区峡谷地形的大跨度桥梁[7,23]。同时,考虑到与平原或沿海地区的桥梁交通量相比,位于山区峡谷桥梁的交通流量较小,且桥上发生严重拥堵的情况也较少,最终选择了稀疏和轻微拥堵这2 种交通流状况。稀疏交通流和轻微拥堵交通流的车流密度分别为12 辆/km 和25 辆/km,这两种交通流均包含7 种车辆类型,分别为2 轴轿车(V1)、2 轴货车(V2)、3 轴拖车(V3)、3 轴整车(V4)、4 轴拖车(V5)、5 轴拖车(V6)和6 轴拖车(V7)。这7 种典型车辆车重、轴重、轴距等信息详见参考文献[15]。
2.3 加劲梁纵向振动时频特性
本节首先对比研究了设置液体黏滞阻尼器前后单风荷载作用下加劲梁纵向振动的时频特性。液体黏滞阻尼器在桥塔与加劲梁之间沿加劲梁纵向布置,一侧桥塔布置2 个,全桥总布置4 个,如图6所示。此外,本节试图从定性的角度阐明液体黏滞阻尼器对主梁纵向振动的减振效果,因此本节中含阻尼器工况均采用统一的阻尼器参数:即阻尼系数C=200 kN/(m/s)α,速度指数α=0.4。

图6 液体黏滞阻尼器布置图Fig.6 The layout of the fluid viscous damper
图7(a)对比了设置液体黏滞阻尼器前后20 m/s风速单独作用下加劲梁的纵向位移时程。为了便于观察,图7(a)还给出了200~260 s 时间段内位移时程的放大图。由图可知,阻尼器可以显著降低加劲梁纵向位移的幅值:设置阻尼器前,加劲梁纵向位移极值为4.52×10-2m,出现在t=230 s 时刻;设置阻尼器后,加劲梁纵向位移极值由4.52×10-2m 降至2.61×10-2m,降幅为42.2%。图7(b)进一步对比了设置阻尼器前后加劲梁纵向位移的频谱图。图中显示:风致加劲梁纵向振动的能量主要集中在0.13 Hz 附近,设置阻尼器后,0.13 Hz 对应的幅值(或能量)由1.20×10-2m2/s 降至6.15×10-3m2/s,降幅为48.9%;此外,设置阻尼器后,风致加劲梁纵向振动能量对应的其余几个频率的幅值也都呈现出不同程度的降低。另外,本文还计算了有无阻尼器在常遇风速(5 m/s)下加劲梁的纵向位移时程和频谱曲线,其规律与20 m/s 风速下的规律(图7)相似。
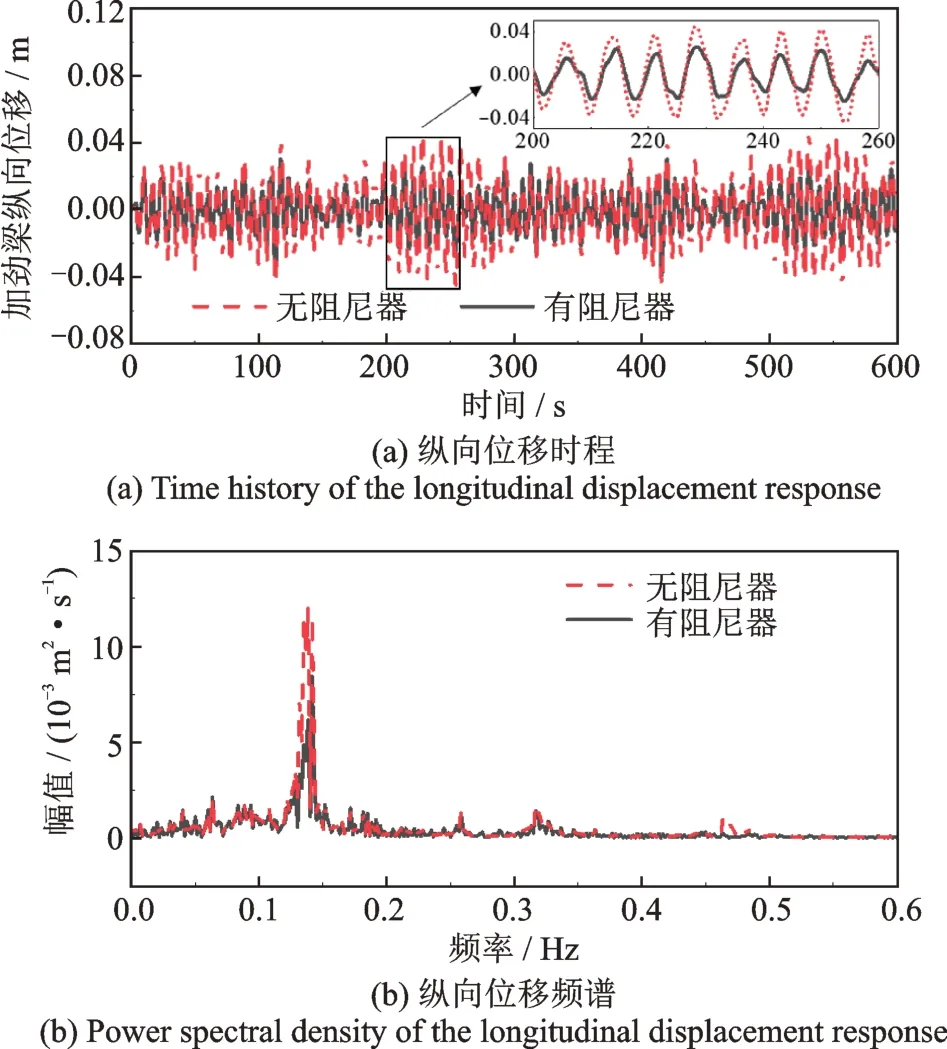
图7 20 m/s 风速下有无阻尼器加劲梁纵向位移时程和频谱对比曲线Fig.7 The longitudinal displacement time history and spec⁃trum of the stiffening girder under mean wind speed of 20 m/s with and without the fluid viscous damper
图8(a)给出了设置液体黏滞阻尼器前后稀疏交通流单独作用下加劲梁纵向位移时程的对比图。从整体图和140~200 s 时间段的放大图可以明显看出,阻尼器不仅可以降低加劲梁纵向位移的幅值,同时也显著降低了加劲梁纵向振动的频率。从纵向振动的幅值来看:设置阻尼器前,加劲梁纵向位移极值为6.63×10-2m,出现在t=180 s 时刻;设置阻尼器后,加劲梁纵向位移极值降至4.38×10-2m,降幅为33.9%。从纵向振动的频率上看(图8(a)放大图):液体黏滞阻尼器起了“低通滤波器”的作用,即纵向振动的高频部分被有效“截止”了,而纵向振动的低频部分则被“保留”。上述规律也可在加劲梁纵向位移频谱图上(图8(b))看出:设置阻尼前,车致加劲梁纵向振动的前5 个主频按幅值(或能量)高低依次为0.47,0.11,0.08,0.05 和0.03 Hz;设置阻尼器后,纵向振动的前5 个主频中只有最高的主频(0.47 Hz)对应的幅值下降显著,由4.88×10-3m2/s 降至2.99×10-4m2/s,降幅为93.88%;而其余4 个较低主频的幅值几乎没有变化。由此可见,车致加劲梁纵向振动的低频部分没有变化,而高频部分则被过滤掉了。此外,本文还计算了有无阻尼器在轻微拥堵交通流作用下加劲梁的纵向位移时程和频谱曲线,其规律与稀疏交通流作用下得到的规律(图8)类似。

图8 稀疏交通流作用下有无阻尼器加劲梁纵向位移时程和频谱对比曲线Fig.8 The longitudinal displacement time history and spec⁃trum of the stiffening girder under free-flow traffic load with and without the fluid viscous damper
图9(a)给出了设置液体黏滞阻尼器前后20 m/s风速与稀疏交通流联合作用下加劲梁纵向位移时程的对比图。从整体图和200~260 s 时间段的放大图可以明显看出,阻尼器可以同时降低加劲梁纵向振动的幅值和频率,其规律与车致加劲梁纵向减振相同(图8)。纵向振动幅值降低方面:加劲梁纵向位移极值由不设置阻尼器时的8.60×10-2m(t=209 s)降至设置阻尼器后的5.61×10-2m(降幅为34.74%)。纵向振动频率降低方面:设置阻尼前,车致加劲梁纵向振动的前5 个主频按幅值(或能量)高低依次为0.47,0.14,0.08,0.05 和0.03 Hz。设置阻尼器后,纵向振动的最高主频0.47 Hz 的幅值由4.75×10-3m2/s 降至5.45×10-4m2/s,降幅为88.53%;次高主频率0.14 Hz 的幅值由5.82×10-3m2/s 降至1.39×10-3m2/s,降幅为76.12%;其余3个较低主频对应的幅值没有变化。

图9 20 m/s 风速与稀疏交通流联合作用下有无阻尼器加劲梁纵向位移时程和频谱对比曲线Fig.9 The longitudinal displacement time history and spec⁃trum of the stiffening girder under mean wind speed of 20 m/s and free-flow traffic load with and without the fluid viscous damper
上述计算结果表明:对于风、车流单独以及联合作用下加劲梁纵向振动,阻尼器均能有效降低纵向振动的幅值;但能否降低纵向振动的频率取决于纵向振动中主频的成分,只有当纵向振动中主频的频率超过某一阈值,阻尼器才能有效地“截止”该高频成分,达到降低纵向振动频率的作用。以本文算例为例:风致加劲梁纵向振动的主频仅有1 个,为0.14 Hz,由于该频率低于阈值,因此阻尼器仅降低了风致加劲梁纵向振动的幅值;车流荷载单独作用以及风和车流荷载联合作用下加劲梁纵向振动中包含0.47 Hz 在内的多个主频成分,由于0.47 Hz 高于阈值,所以阻尼器可以同时降低加劲梁纵向振动的幅值和频率。
3 阻尼器参数敏感性及优化分析
本节将研究液体黏滞阻尼器参数的不同取值对加劲梁位移和塔底内力的影响规律。其中,加劲梁的位移包含了纵向位移极值和纵向累积位移,这两项指标对于行车舒适性和梁端伸缩缝的使用寿命均有重要的影响;塔底内力包含了桥塔底部的沿纵桥向剪力和绕横桥向弯矩,这两项指标直接影响着桥塔的受力状态与工作性能。液体黏滞阻尼器的参数取值如下:阻尼系数C取值为50,100,200,500,750 和1000 kN/(m/s)α,速度指数α的取值区间为0.1~0.8,间隔为0.1,共计48 组参数组合。在此基础上,以位移和内力为优化目标,提出了液体黏滞阻尼器参数的合理取值范围。
3.1 位移分析
图10(a)~(c)分别给出了20 m/s 风速单独作用、稀疏交通流单独作用、以及20 m/s 风速与稀疏交通流联合作用下加劲梁纵向累积位移极值随阻尼器参数不同取值的变化曲面。图10(a)~(c)可知,三种不同的荷载工况下,加劲梁纵向位移极值随阻尼器参数不同取值的变化趋势基本相同:随着阻尼系数C的增大和速度指数α的减小,加劲梁纵向位移极值呈减小趋势,且减小的速率先小后大。

图10 不同阻尼系数和阻尼指数组合下加劲梁纵向累积位移极值曲面图Fig.10 The surface plot of maximum longitudinal displacement of the stiffening girder under various combinations of damping co⁃efficients and damping exponent
当阻尼系数C为1000 kN/(m/s)α,速度指数α为0.1 时,三种不同的荷载工况下,加劲梁纵向位移极值达到最小:20 m/s 风速单独作用下,加劲梁纵向累积位移极值由不设置阻尼器的4.56×10-2m 降至3.2×10-3m,降幅为92.88%;稀疏交通流单独作用下加劲梁纵向累积位移极值由不设置阻尼器的6.87×10-2m 降至5.25×10-2m,降幅为23.58%;20 m/s 风速与稀疏交通流联合作用下加劲梁纵向累积位移极值由不设置阻尼器的1.03×10-1m 降至6.80×10-2m,降幅为33.98%。对比三种荷载工况下阻尼器纵向振动的减振效果表明:在取相同的阻尼器参数下,阻尼器对风致纵向振动极值的减振效果要远好于其余两种工况。
图11(a)~(c)分别给出了20 m/s 风速单独作用、稀疏交通流单独作用、以及20 m/s 风速与稀疏交通流联合作用下加劲梁纵向累积位移随阻尼器参数不同取值的变化曲面。图中所指的累积位移均指换算成1 天后的累积位移。
由图11(a)可知,20 m/s 风速单独作用下,随着阻尼系数C的增大和速度指数α的减小,加劲梁纵向累积位移先缓慢减小,后迅速减小,即减小的速率先小后大。与风荷载单独作用的工况不同,对于车流荷载单独作用以及风和车流荷载联合作用的工况,加劲梁纵向累积位移随着阻尼系数C的增大和速度指数α的减小虽也呈减小趋势,但减小的速率先大后小,如图11(b)和图11(c)所示。

图11 不同阻尼系数和阻尼指数组合下加劲梁纵向累积位移极值曲面图Fig.11 The surface plot of longitudinal cumulative displacement of stiffening girder under various combinations of damping coeffi⁃cients and damping exponent
当阻尼系数C为1000 kN/(m/s)α,速度指数α为0.1 时,三种不同的荷载工况下,加劲梁纵向累积位移极值达到最小:20 m/s 风速单独作用下,加劲梁纵向累积位移极值由不设置阻尼器的1.268 km降至0.072 km,降幅为94.32%;稀疏交通流单独作用下加劲梁纵向累积位移极值由不设置阻尼器的1.407 km 降至0.314 km,降幅为77.68%;20 m/s 风速与稀疏交通流联合作用下加劲梁纵向累积位移极值由不设置阻尼器的1.895 km 降至0.317 km,降幅为83.27%。
上述计算结果表明阻尼器对于三种荷载工况下加劲梁纵向累积位移均有较好的减振效果:在取相同的阻尼器参数下,阻尼器对加劲纵向累积位移的减振效果依次为风荷载单独作用工况、风和车流联合作用工况和车流单独作用工况。
3.2 内力分析
由于绕横桥向弯矩与沿纵桥向剪力的比值为一常量(加劲梁与塔底的竖向距离),因此本文仅以绕横桥向弯矩(下文简称塔底纵向弯矩)为例,分析了不同阻尼器参数对各荷载工况下塔底纵向弯矩的影响规律。
图12(a)~(c)分别给出了20 m/s 风速单独作用、稀疏交通流单独作用、以及20 m/s 风速与稀疏交通流联合作用下塔底纵向弯矩随阻尼器参数不同取值的变化曲线。图12 中的虚线为不设置液体黏滞阻尼器时,相对应荷载工况下的塔底纵向弯矩。
由图12(a)可知,随着阻尼系数C的减小,速度指数α的增大,塔底纵向弯矩先迅速降低并低于不设置阻尼器时的塔底弯矩(3.11×108N·m),然后有轻微回升,但总体趋于平稳且小于不设置阻尼器时的塔底弯矩。当阻尼系数C较大且速度指数α<0.5时,塔底纵向弯矩会超过不设置阻尼器时的塔底弯矩。当阻尼系数C为1000 kN/(m/s)0.7,速度指数α为0.7 时,塔底纵向弯矩取得最小值(2.94×108N·m),与不设置阻尼器的塔底纵向弯矩相比,此时阻尼器的减振率为5.47%。

图12 不同阻尼系数和阻尼指数组合下塔底纵向弯矩曲线Fig.12 The bending moment of the tower base varying with different combinations of damping coefficients and damping exponent
由图12(b)可知,对于车流荷载引起的塔底纵向弯矩,设置阻尼器后均能进行有效的减振,但不同阻尼器参数取值下的减振规律不同。当阻尼系数C≤100 kN/(m/s)α时,随着速度指数α的增大,塔底纵向弯矩逐渐增大;当阻尼系数C>100 kN/(m/s)α时,随着速度指数的增大,塔底纵向弯矩先减小后增大,表明此时阻尼器参数存在一个较优的区间。当阻尼系数C为500 kN/(m/s)0.4,速度指数α为0.4时,塔底纵向弯矩取得最小值(8.03×108N·m),与不设置阻尼器时的塔底纵向弯矩(1.09×109N·m)相比,此时阻尼器的减振率为26.40%。
由图12(c)可知,对于风荷载与车流荷载引起的塔底纵向弯矩,设置阻尼器后也都能进行有效的减振,但减振的程度取决于阻尼器的参数取值。当阻尼系数C<750 kN/(m/s)α时,随着速度指数的增大,塔底纵向弯矩先减小后增大;当阻尼系数C≥750 kN/(m/s)α时,随着速度指数的增大,塔底纵向弯矩先迅速减小,后趋于平稳。当阻尼系数C为100 kN/(m/s)0.4,速度指数α为0.4 时,塔底纵向弯矩取得最小值(6.37×108N·m),与不设置阻尼器时(8.48×108N·m)相比,此时阻尼器的减振率为24.88%。
3.3 参数优化
通过分析不同阻尼器参数对各荷载工况下加劲梁位移和塔底纵向弯矩的影响规律可知:加劲梁纵向位移极值与纵向累积位移均随着速度指数α的减小而减小,因此速度指数α宜取小一些,但过小的速度指数α对阻尼器的加工制造提出了考验,同时提高了制造成本,一般在实际工程中取为0.3~0.5[24]。此外,加劲梁纵向位移极值与纵向累积位移均随着阻尼系数C的增大而减小,但过大的阻尼系数C会导致塔底纵向弯矩增大,所以阻尼系数C也不宜过大。因此,需对液体黏滞阻尼器的设计参数进行合理优化,以达到降低加劲梁纵向振动响应、优化塔底的受力状态和降低该阻尼器制造成本的目的。
本节拟采用响应面优化法(Response Surface Method,也称响应面法)对液体黏滞阻尼器参数进行优化。响应面法的基本思想是通过近似构造一个具有明确表达式的多项式来表达隐式功能函数,它采用简单的显式函数来模拟实际结构复杂的输入输出关系,是一种试验条件寻优的方法,适用于解决非线性数据处理的相关问题[25]。基于响应面法的液体黏滞阻尼器参数优化分析流程如图13 所示,简述如下:首先采用响应面法对多个目标工况下的数值进行非线性曲线拟合,一个目标工况对应一个响应面函数。其次,采用单点最大相对误差(ME)与决定系数(R2)评价响应面的拟合效果。若响应面精度不满足要求,则需要对目标工况的数据重新进行非线性曲线拟合,直至精度满足要求;在此基础上,通过极值线性模式对响应面函数(本文采用二次多项式)进行归一化。随后,在确定多个目标工况各自的权重系数后,运用线性加权和法将各目标工况对应的响应面函数(二次多项式)进行线性叠加。最后,采用遗传算法对叠加后的新多项式进行参数最优化分析。本文共选取了9 个目标工况,如表1所示。

图13 参数优化分析流程图Fig.13 Flowchart of parameter optimization procedure
响应面函数形式的选取一般应遵循以下两个原则:(1)响应面函数应尽可能准确地模拟实际结构输入与输出之间的关系;(2)响应面函数应尽量简洁以提高计算效率。本文采用了响应面法中广泛采用的二次多项式,其表达式如下:

响应面函数的评价指标可用来评价响应面函数与实际数据的拟合程度和有效性。常用的指标有单点最大相对误差(ME)与决定系数(R2),其表达式如下:

式中k为由试验设计确定的参数分组数;yi为第i组参数对应的实际响应值为第i组参数对应的响应面模型计算值为所有k组参数实际响应的平均值。
由上式可知,ME的值非负(ME≥0),R2的值介于0~1 之间。当ME趋近于0,R2趋近于1 时,表明响应面的拟合精度高。通常要求ME≤10%,R2≥0.9。
本文共选取了9 个目标工况,分别对应了风、车流荷载单独以及联合作用下的纵向累积位移、纵向位移极值以及塔底纵向弯矩,如表1所示。此外,表1还列出了上述9 种目标工况下响应面的拟合结果。限于篇幅,本文仅以风与车流荷载联合作用工况下加劲梁纵向位移极值为例,给出了响应面的拟合结果,如图14 所示。由表1和图14 可知,对于所有的9个目标工况,响应面的拟合效果均较好。

表1 目标工况下响应曲面拟合结果Tab.1 Fitting performance of the response surfaces for target loading scenarios

图14 风与车流荷载联合作用下加劲梁纵向位移极值拟合Fig.14 Fitting results of the maximum longitudinal displace⁃ment of stiffening girder under combined wind and free-flow traffic loads
由于目标工况的数据具有不同的量纲,在对目标工况的响应面函数运用线性加权和法之前,需首先对目标工况的数据进行无量纲化处理。本文通过极值线性模式将上述9 个二次多项式进行无量纲化(或归一化)处理。其中,极值线性模式的转换规则如下:

式中An为新数据,位于[0,1]之间;A0为原数据;max为所有数据中的最大值;min为所有数据中的最小值。
在进行无量纲化处理后,采用线性加权和法将上述9 个工况对应的响应面函数(二次多项式)进行线性叠加。其中,各多项式的权重系数由液体黏滞阻尼器的设计参数(阻尼系数C、速度指数α)对位移、内力指标的影响程度决定。在本研究中,认为阻尼器设计参数对2 项位移指标和2 项内力指标的影响程度相同;同时考虑到2 项内力指标中的塔底纵向剪力与纵向弯矩的变化相同,只需要考虑其中1项内力指标并将其权重系数加倍即可。基于上述考虑,最终将各工况下的纵向位移极值和纵向累积位移的权重系数确定为1/12,将各工况下的塔底纵向弯矩的权重系数确定为1/6,所有9 种目标工况的权重系数之和为1。
最后,通用编程软件MATLAB 调用遗传算法[25],对采用线性加权和法得到的响应面函数(二次多项式)进行参数最优化分析,优化目标是使该二次多项式的值最小,即所有目标工况下加劲梁纵向位移极值、纵向累积位移和塔底纵向弯矩均较小,以达到优化全桥结构受力、降低纵向振动响应的目的。优化分析结果表明,液体黏滞阻尼器的最优参数为:阻尼系数C为670 kN/(m/s)0.38,速度指数α为0.38。因此液体黏滞阻尼器参数建议取值区间为:阻尼系数C宜取500~700 kN/(m/s)α,速度指数α宜取0.3~0.5。
4 结 论
本文以某在建大跨公路悬索桥为工程背景,研究了运营阶段风荷载与车流荷载不同组合下加劲梁纵向振动响应的时频特性,分析了液体黏滞阻尼器的纵向减振效果,并进一步对液体黏滞阻尼器的参数进行了优化。得出如下结论:
(1)对于风、车流单独以及联合作用下加劲梁纵向振动,阻尼器均能有效降低纵向振动的幅值;但能否降低纵向振动的频率取决于纵向振动中主频的成分,只有当主频频率超过某一阈值,阻尼器才能有效地“截止”该高频成分,达到降低振动频率的作用。例如,风致加劲梁纵向振动的主频低于阈值,因此阻尼器仅降低其纵向振动的幅值;而车流荷载单独作用以及风和车流荷载联合作用下加劲梁纵向振动中包含高于阈值的主频,所以阻尼器可以同时降低其幅值和频率。
(2)设置液体黏滞阻尼器后,风、车流荷载单独或者联合作用下,加劲梁纵向位移极值和纵向累积位移均随着阻尼系数C的增大和速度指数α的减小呈减小趋势。此外,在阻尼器参数相同取值下,阻尼器对风致纵向振动的极值以及纵向累积位移的减振效果要好于其余两种荷载工况。
(3)不同荷载工况下液体黏滞阻尼器对塔底纵向弯矩的影响规律不同:风荷载单独作用下,设置阻尼器后可能会增大塔底的纵向弯矩;而对于车流荷载单独作用或者风、车流联合作用工况,设置阻尼器后可降低塔底的纵向弯矩。
(4)以优化全桥结构受力、降低纵向振动响应为目标,采用响应面法对液体黏滞阻尼器的参数进行优化分析。优化分析结果表明,液体黏滞阻尼器参数建议取值区间为:阻尼系数C宜取500~700 kN/(m/s)α,速度指数α宜取0.3~0.5。

