突破函数与导数问题的几种策略

李红磊

(宁夏回族自治区银川市灵武市第一中学)

对于同一问题的思考,不同的学生可能会有不同的想法,而且导数与函数的综合问题题型多变、方法灵活,不同的方法繁简差异很大,因此笔者建议学生在解题之前要多想少算,先想再算.

1 对数分离，指数合并

利用导数处理函数问题的关键是求函数的单调区间、极值和最值.求函数的单调区间需要判断导函数的正负,求导函数的零点,即求解导函数为0的方程.若此方程为超越方程,处理时需先观察函数结构特征,将之转化变形构造新函数再求解.

例1设函数f(x)＝xlnx,若(a≠0)在区间(0,＋∞)上恒成立,求a的取值范围.

若直接作差构造函数g(x)＝xlnx－ax2－,对其求导得g′(x)＝1＋lnx－2ax,令g′(x)＝0,即1＋lnx－2ax＝0,此方程无法求解,所以在求导之前可以先对函数进行变形,然后构造函数,借助所构造函数的单调性解决问题.

原函数中含有xlnx,求导后仍然含有lnx,在求导之前可先将二者分离.

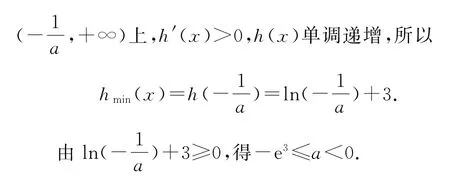
本题所涉及的函数中含有xlnx,因此可先将lnx分离,再构造函数.但恰恰相反的是若函数中含有指数式ex,因其求导后仍为ex,故将ex与其他函数式合并后,反而会简化计算.

2 特值检验，先猜后证

不等式恒成立、能成立问题是高考函数与导数综合问题的常考题型.不等式恒成立,即对于所给区间内的任意x,不等式都成立,那么从给定区间内选取一个特殊值,一定能使不等式成立.类似地,若不等式不是恒成立,则存在某一个值使不等式不成立.因此,在相关问题的求解中,通过选取某些特殊值,往往可以简化计算过程.

例2已知函数f(x)＝aex－1－lnx＋lna,若f(x)≥1恒成立,求实数a的取值范围.

本题属于不等式恒成立问题,可通过构造同构函数处理,但计算烦琐,且对学生解题技能要求较高,因此采用直接求最值的方法求解.

函数f(x)的定义域为(0,＋∞),即任意的x∈(0,＋∞),f(x)≥1恒成立.将x＝1代入不等式f(x)≥1,得a＋lna≥1,即a≥1,接下来只需证明当a≥1时,f(x)≥1即可.

因为当a≥1 时,f(x)＝aex－1－lnx＋lna≥ex－1－lnx,因此只需证明ex－1－lnx≥1即可.

设g(x)＝ex－1－lnx,则,易得当x＝1时,g′(x)＝0,又,所以g′(x)单调递增,所以x＝1是g′(x)＝0唯一的根.所以在(0,1)上,g′(x)＜0,g(x)单调递减,在(1,＋∞)上,g′(x)＞0,g(x)单调递增,所以g(x)≥g(1)＝1.

本题也可采用放缩法证明,即利用不等式ex≥x＋1,当x＝1时,取等号,将其中的x换为lnx,得x≥lnx＋1,综合上面两个不等式可得ex－1－lnx≥x－lnx≥1.

3 三思后行，不盲目求导

在处理函数与导数的综合问题时,很多学生习惯直接求导,导致求导后对参数的讨论情况较多,甚至不易讨论.其实有些情况在求导之前就能讨论清楚,因此我们要克服这种思维定势,三思后行.

例3判断函数f(x)＝acosx＋xsinx,x∈的零点个数.

直接求导可得f′(x)＝－asinx＋sinx＋xcosx＝(1－a)sinx＋xcosx,此时欲判断导函数的符号,需要讨论的情况较多.

对于没有限制条件的参数问题,分类的标准通常是三类,即大于0、小于0、等于0.

当a＝0时,f(x)＝xsinx,易知其在上只有一个零点,即x＝0.

当a＞0时,在上,acosx＞0,xsinx≥0,即f(x)＞0恒成立,所以此时f(x)没有零点.

这两种情况在求导之前就完全能够讨论清楚,下面只需对a＜0的情况进行判断即可.

当a＜0时,f′(x)＝(1－a)sinx＋xcosx,易知f′(0)＝0,且在)上,f′(x)＜0,f(x)单调递减;在)上,f′(x)＞0,f(x)单调递增.又f(0)＝,所以此时函数f(x)在上有两个零点.

求解以三角函数为背景的导数综合问题常用的方法是分区间讨论法,即寻找原函数或导函数恒正或恒负的区间,而有些情况需要在求导之前讨论,因此解答此类问题时切不可盲目求导.

4 变量设参，反客为主

与导数有关的问题,大多含有参数,通常我们是将x视为主元.在某些情况下,若将参数视为主元,往往可起到化繁为简的功效.

例4已知a＞0,函数f(x)＝ax2－x,g(x)＝lnx.若不等式f(x)≥g(ax)在(0,＋∞)上恒成立,求a的值.

f(x)≥g(ax),则ax2－x－ln(ax)≥0,令m(x)＝ax2－x－ln(ax),则

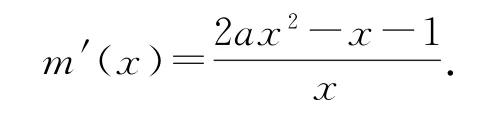
令m′(x)＝0,即2ax2－x－1＝0,此方程为一元二次方程,要结合判别式及根与系数的关系讨论其零点的存在情况,因此不妨将a视为主元,进而构造函数,利用导数研究所构造函数的单调性进行求解.

将ax2－x－ln(ax)≥0 中的a视为主元,令m(a)＝ax2－x－ln(ax),则问题转化为mmin(a)≥0.

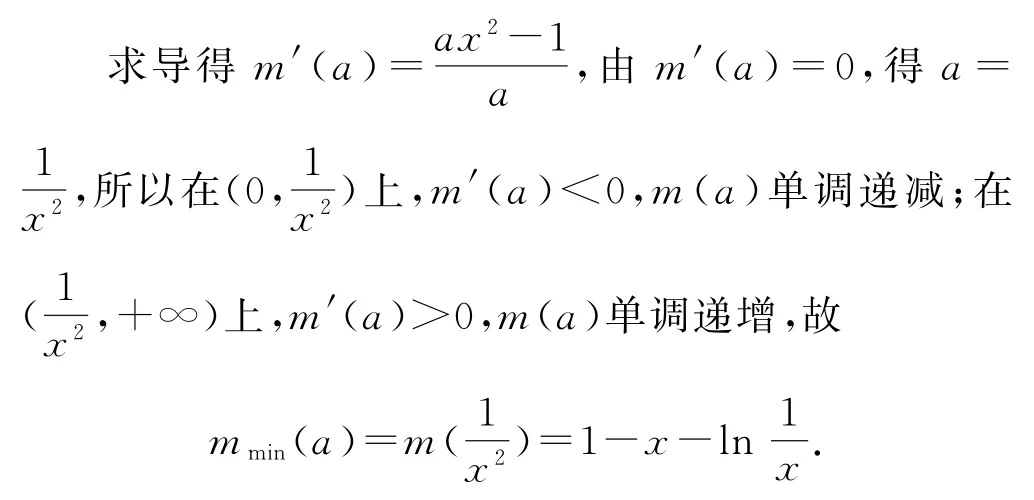
设h(x)＝1－x－ln＝1－x＋lnx,则,所以在(0,1)上,h′(x)＞0,h(x)单调递增;在(1,＋∞)上,h′(x)＜0,h(x)单调递减,所以hmax(x)＝h(1)＝0,mmin(a)≤0.

但我们所要的关系式是mmin(a)≥0,故只有mmin(a)＝0时,同时满足两式,此时且x＝1,故a＝1.

题目中的常量与变量是相对的,并没有指定哪个量一定为主元,因此根据解题的需要,若将常量与变量易位思考,可能会起到化难为易之效.

当然,类似的问题还有很多,比如求导之前观察所给函数是否能直接得出零点,这些点就是我们后续解题的关键.函数是否具有奇偶性,若具有,则求函数的单调区间、极值和最值,判断其零点个数均在y轴右侧即可.动笔之前先将这些问题考虑清楚,可收获事半功倍的效果.

(完)