典型激励下调谐质量惯容系统TMIS 的轻量化结构控制

张瑞甫，曹嫣如，潘 超，胡岫岩

(1. 同济大学土木工程防灾国家重点实验室，上海 200092；2. 同济大学结构防灾减灾工程系，上海 200092；3. 烟台大学土木工程学院，烟台 264005)

结构振动控制技术[1-3]是降低结构在地震、风等动力荷载作用下结构动力响应的有效手段。从控制原理的角度，结构振动控制技术可以分为隔振技术、消能减振技术和动力吸振技术三大类。其中，动力吸振技术是通过在主结构上附加调谐质量减振系统来吸收和耗散主体结构的振动能量[4-5]。由于调谐质量减振系统的振动控制效果与附加调谐质量的大小相关，在结构振动控制需求较高时，需要减振子系统具备较大的附加质量。过大的附加质量不仅占据了结构宝贵的使用空间、提高了工程造价，在施工、检修、更换时也较为不便；而且，较大的附加质量甚至可能在地震作用下给结构带来不利影响[6-7]。此外，目前结构本身正朝着轻量化、柔性化、大跨度的趋势发展，与之相应的结构振动控制系统亦将趋于轻量化、小型化、高效化。惯容元件(图1)是一种在经典力学理论中没有的元件，元件出力与其两端点间的相对加速度相关。以惯容为核心元件的结构振动控制装置称为惯容系统，可以从惯性、刚度、阻尼三个方面对结构的动力特性进行灵活调整[8-9]，具有表观质量增效[10-13]、耗能增效[8,14]等控制特性，已被证明是一种高效的结构振动控制装置[14-17]，近年来开始受到科研人员的重点关注[18-20]。既有试验表明惯容元件的表观质量(又称惯容系数)已可以达到元件重力质量的数千倍[21]。在调谐质量减振装置中引入惯容元件，利用惯容的表观质量增效作用减小所需的附加调谐质量，可以为结构振动控制提供一种新的轻量化调谐减震方案，提供更加经济、高效地实现结构振动控制手段。目前，已有学者将惯容元件与调谐质量减振装置进行组合，并开展了初步研究。Garrido 等[22]提出了称为旋转惯性双调谐质量阻尼器(Rotational inertia double tuned mass damper, RIDTMD，图2)的振动控制装置。该装置将经典调谐质量阻尼器(TMD)中的耗能元件替换为惯容系统，在相同附加质量的情况下，减震效果比经典TMD 更佳。Marian 等[23-26]利用惯容元件的表观质量增效特点，提出了调谐质量阻尼惯容系统(Tuned mass damper inerter, TMDI，图3)，该系统是在经典TMD 的基础上增加一个接地的惯容元件，以替代部分调谐质量，实现轻量化调谐减振。

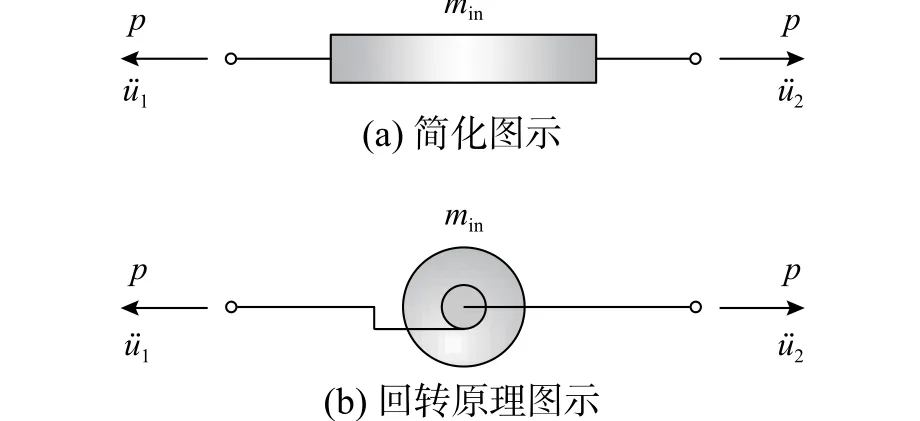
图1 两端点加速度相关型结构控制元件——惯容Fig. 1 Two-terminal acceleration related structural control element -- inerter

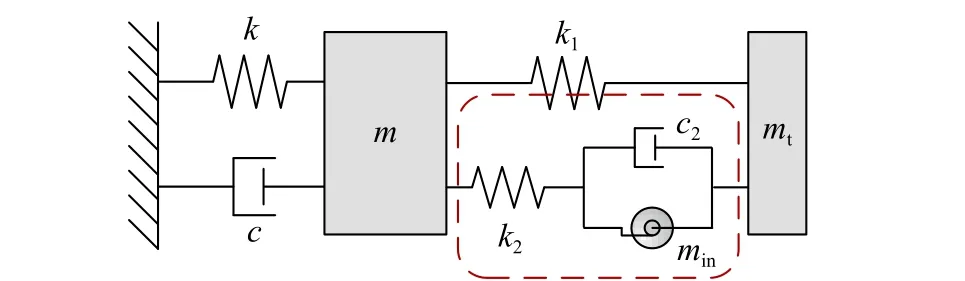
图2 附加旋转惯性双调谐质量阻尼器(RIDTMD)的单自由度体系示意图Fig. 2 SDOF system with RIDTMD

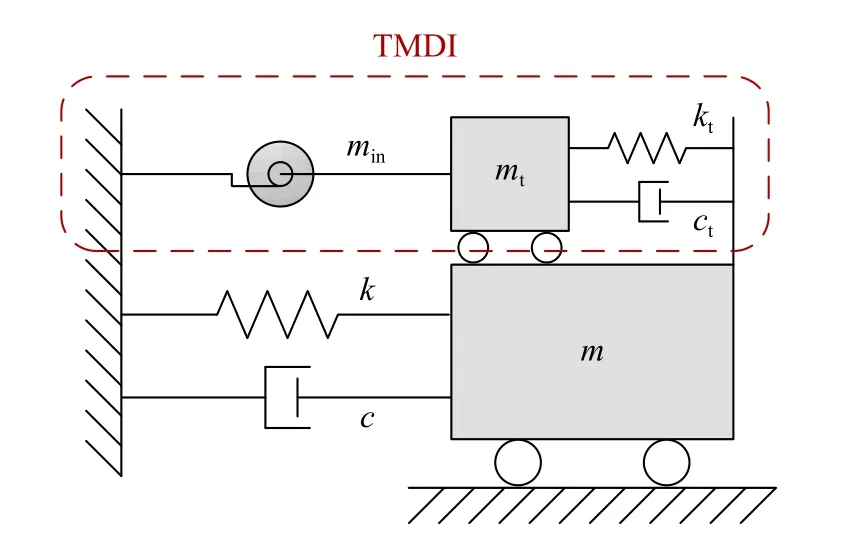
图3 附加调谐质量阻尼惯容系统(TMDI)的单自由度体系示意图Fig. 3 SDOF system with TMDI

上述研究表明：在经典的调谐质量减震(振)系统中加入惯容元件，可以有效地提高减震(振)系统的振动控制效率，具有广泛的应用前景。然而，Garrido 等[22]针对RIDTMD 的研究虽然证实了其振动控制效果的提升，但并未指出惯容元件为调谐型减震(振)系统带来的轻量化效应。对于TMDI 系统，虽然已经指出其轻量化的潜力，但TMDI 需要将惯容元件直接与地面相连，在实际应用中对于大量形式多样的结构而言，这种连接方式具有显著的局限性，尤其当结构薄弱层不在底层时将造成应用上的不便。从力学原理上说，TMDI 将惯容元件直接与地面相连的做法导致惯容元件退化成了绝对加速度相关的普通质量元件，其力学原理与TMD 并无实质上的区别。即TMDI主动丢弃了惯容最特殊的力学特性——两端点惯性特性，意味着惯容本身的调谐和耗能增效特性难以发挥。相较之下，RIDTMD 的拓扑形式更能让惯容元件充分发挥功能。本文在RIDTMD 力学模型的基础上进行进一步的抽象和凝练，针对适于结构典型灾种激励下提出如图4 所示的具有调谐质量轻量化特征的广义调谐质量惯容减振系统(Tuned mass inerter system, TMIS)，及其对应的基于性能需求的设计方法。该系统具有更加灵活的安装形式，惯容子系统也可以选择不同类型，以适用于不同的应用场景。与传统视角不同，本文从轻量化结构控制的角度分析和探讨TMIS 的基本理论、结构形式与设计方法，以充分体现惯容元件的表观质量增效特性带来的结构振动控制轻量化优势，分析TMIS 在不同灾种工况下的结构振动控制性能，以证明TMIS 的广泛适用性；通过与安装TMD 的结构进行比较，证实在不同激励下TMIS 所具有的轻量化控制优势。

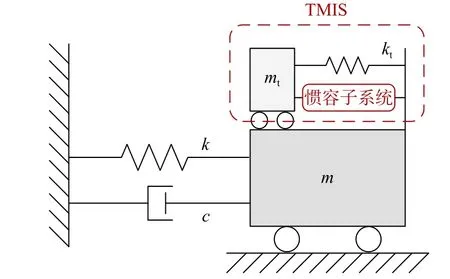
图4 广义调谐质量惯容系统(TMIS)Fig. 4 Generalized tuned mass inerter system (TMIS)

1 调谐质量惯容系统(TMIS)基本原理

1.1 TMIS 力学模型

惯容系统可由最基本的三个力学元件构成：惯容元件、阻尼元件和弹簧元件。在这些力学元件中，惯容元件具有显著的表观质量增效作用，在不显著增加主体结构附加质量的前提下可有效地调整结构的惯性特征并吸收结构振动能量[9,14]。利用这种具有表观质量增效特性的元件，惯容系统相较于传统的调谐质量减振装置可以提供相同甚至更高的减振效果并显著地降低结构的附加调谐质量需求，从而实现轻量化调谐减震，对调谐质量减震(振)系统的实际应用具有重要意义。

图5 给出了附加经典TMD 的单自由度体系力学模型，以便与图4 中TMIS 的结构形式进行对比。TMIS 由调谐质量mt、调谐弹簧kt和惯容子系统组成，图6(a)给出一种较为典型的惯容子系统包括并联连接的惯容元件min与阻尼元件cin，以及与它们串联连接的弹簧元件kin，该种惯容子系统又称为SPIS-II (Series-parallel layout II inerter system)型惯容系统[27-28]。除此以外，TMIS 中惯容子系统还可以有如图6(b)所示等其它力学拓扑形式。本文主要以图6(a)的形式作为示例，对具有轻量化特征的TMIS 进行系统研究和说明。

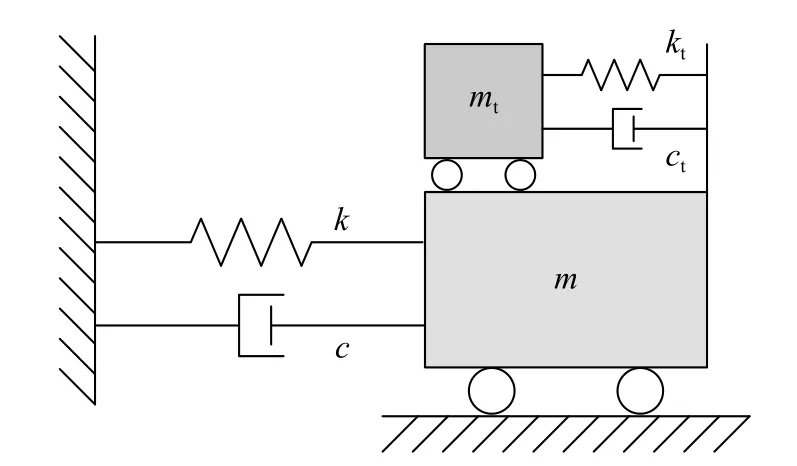
图5 附加TMD 单自由度体系的力学模型Fig. 5 SDOF systems with TMD

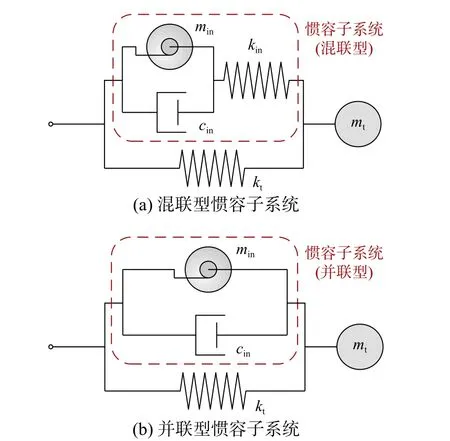
图6 本文所示例的两类TMIS 的力学模型Fig. 6 Mechanical models of two types of TMIS applicated in this research

1.2 附加TMIS 的单自由度体系运动方程

根据图6 所示的TMIS 力学模型，附加TMIS的单自由度体系力学示意图如图7 所示。其中，图7(a)中使用了图6 的混联型惯容子系统，其运动方程如式(1)所示；图7(b)中使用了图6(b)的并联型惯容子系统，其运动方程如式(2)所示。

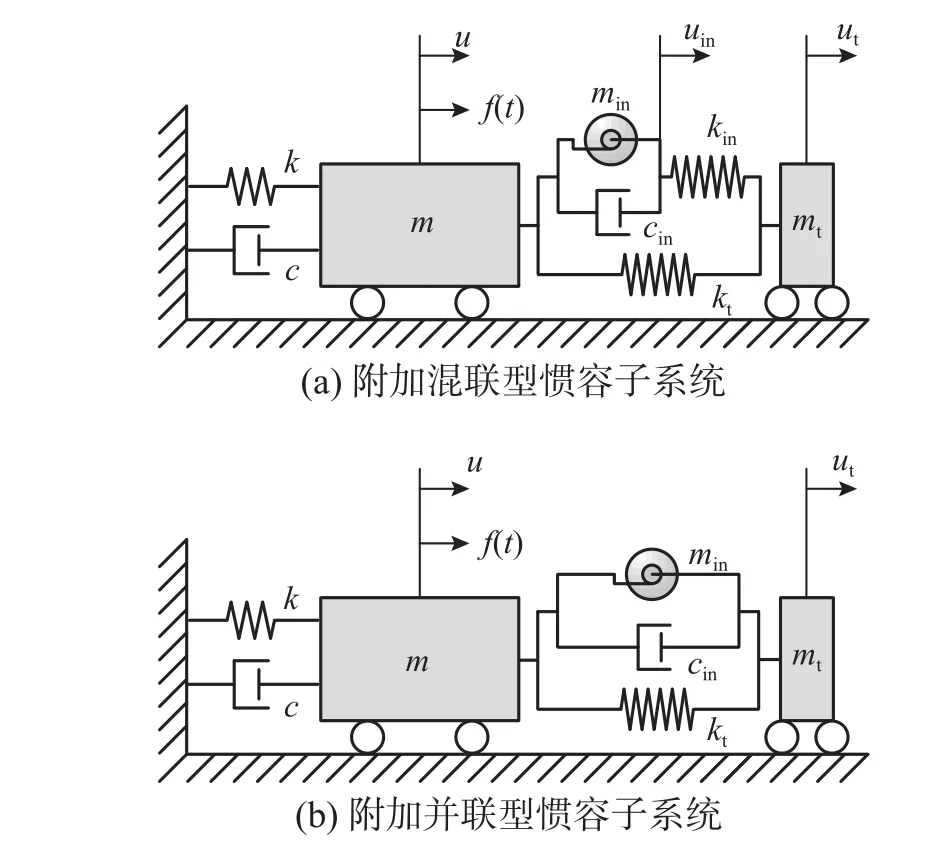
图7 附加TMIS 单自由度体系力学模型Fig. 7 Mechanical model of TMIS based SDOF system

基于上述无量纲参数，附加TMIS 的单自由度体系(以混联型为例)运动方程可以表达成式(4)，进而表达成如式(5)～式(9)所示的矩阵形式：

1.3 附加TMIS 单自由度体系响应计算

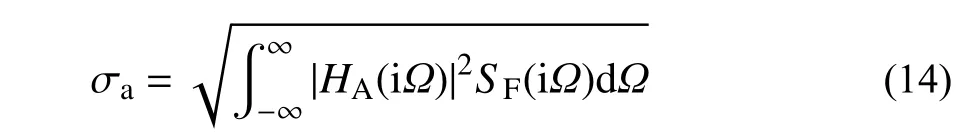
2 典型激励

为了解TMIS 在不同动力激励作用下的轻量化结构减振控制效果，本文选取工程结构设计时经常考虑的地震作用、风荷载、人致激励三种激励作为典型。

2.1 地震作用

2.2 风荷载

由图8 可以看出，风荷载频率主要在0 Hz～1 Hz，因此，在计算风荷载作用下结构动力响应时，仅在该频率范围内进行积分。在风荷载激励下，主要关注结构的加速度响应。采用白噪声激励SF(iΩ)=S0，风荷载作用下附加TMIS 的单自由度体系主结构加速度响应均方根如式(17)：

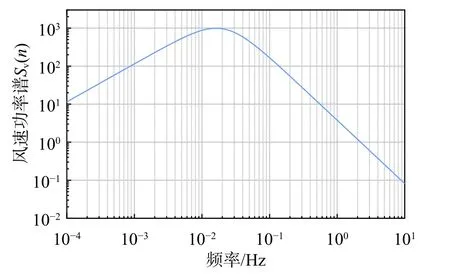
图8 风荷载功率谱Fig. 8 PSD of wind load

2.3 人致激励

在地震作用和风荷载以外，人致激励也将导致结构动力响应，如人致激励[31]会对空间和大跨结构带来振动响应，可能会对结构安全和人员舒适度带来影响。以楼板结构为例，当人员活动产生的振动频率与楼板自振频率接近时可能造成共振现象，研究中常将这种竖向人致激励以式(18)形式表示。人致激励时程曲线如图9 所示。

图9 人致激励时程曲线Fig. 9 Time history curve of human-induced excitation

3 基于结构性能需求的TMIS 参数设计策略

3.1 设计方法

对于结构附加TMIS 的力学元件参数设计，本研究提出一种基于性能需求的优化设计方法。在参数设计过程中，本文将重点关注调谐质量比μt，其反映了附加调谐质量的大小。如1.2 节中式(3)所示，调谐质量比μt为附加调谐质量mt与单自由度主结构质量m的比值。在附加TMIS 的结构运动方程中，惯容元件具有表观质量min，表观质量远大于惯容元件的重力质量，惯容元件的重力质量同结构整体质量和表观质量相比，可忽略不计，所以振动控制系统的质量可以只考虑调谐质量mt。此外，定义减震(振)比 γ作为设计指标，用于反映结构在不同外部激励作用下的性能需求。在地震荷载作用下，减震比 γU定义为附加TMIS 的单自由度结构均方位移响应与无控结构均方位移响应的比值，如式(20)和式(21)所示。在关注结构舒适度的工况下，如风荷载与人致激励，减振比γA定义为附加TMIS 的单自由度结构均方加速度响应与无控结构均方加速度响应的比值，如式(22)～式(24)所示。

式中，下标min、max 分别为TMIS 各元件参数取值上下限。

3.2 参数设计流程

在附加TMIS 的单自由度体系中，TMIS 各参数的优化设计可以按照图10 所示的方法进行。主要步骤为：

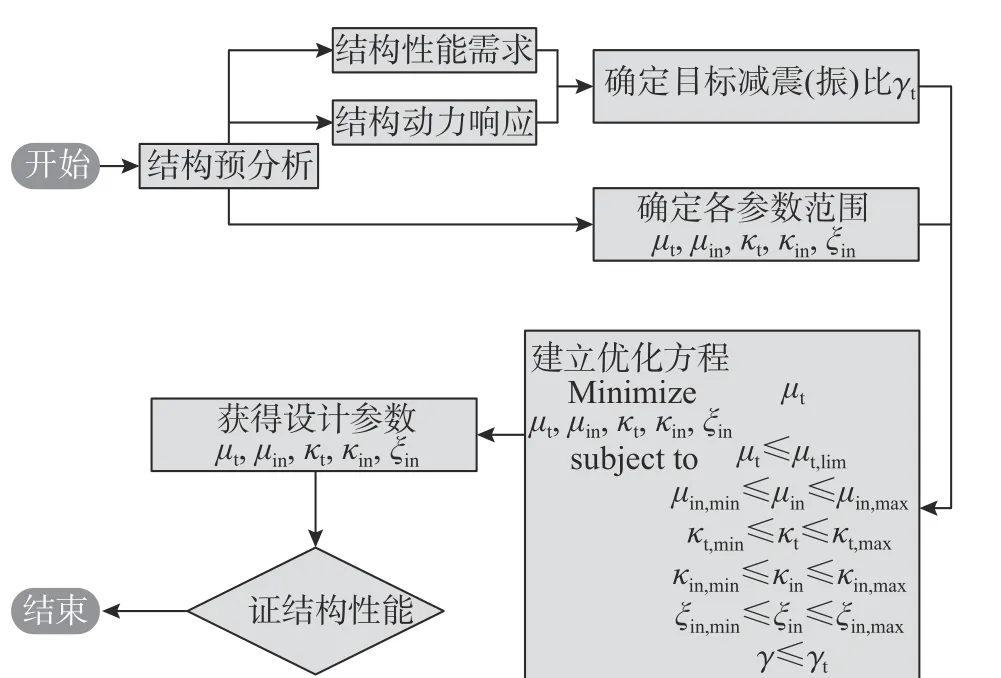
图10 TMIS 参数设计流程图Fig. 10 Flow chart for parameter design of TMIS

1)进行结构预分析，明确结构性能需求，计算原始结构动力响应，确定目标减震(振)比及各参数约束范围；

2)选择设计目标，建立相应优化方程；

3)求解优化方程，获得设计参数；

4)使用获得的参数对结构性能进行验证，若未能达到目标设计要求，则需要进行参数迭代设计。

4 地震作用下TMIS 轻量化控制

4.1 TMIS 结构振动控制效果

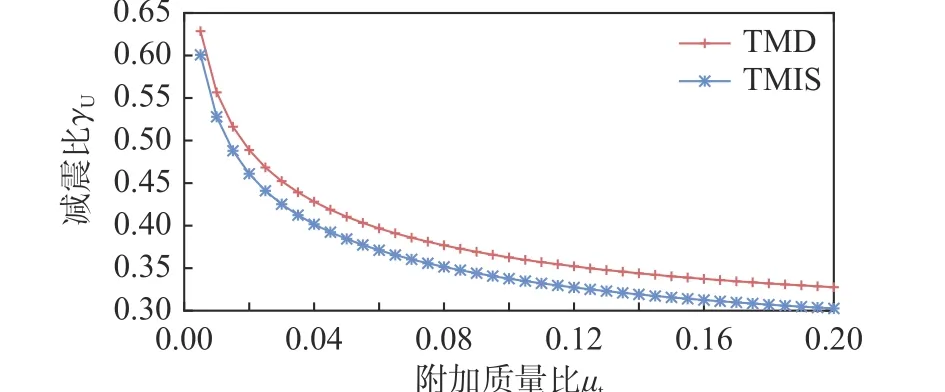
图11 地震作用下附加质量比一定时附加TMD 和TMIS 单自由度结构的最优减震比Fig. 11 Vibration mitigation ratio of SDOF systems with TMD and TMIS under seismic excitation

图12 地震作用下附加质量比一定时TMIS 的性能优化参数Fig. 12 Optimal parameters of TMIS with different additional mass ratio under seismic excitation

4.2 TMIS 的轻量化振动控制效果

本节对比了不同的减震比需求下，TMIS 对于调谐质量系统的轻量化作用。取20 组调谐质量比作为附加TMD 的调谐质量μt,TMD，使用TMD 优化设计公式计算其余设计参数，得到地震作用下附加TMD 单自由度体系的减震比如表1 所示。随后，按照3.1 节式(25)叙述的轻量化设计方法，将附加TMD 结构的减震比作为设计TMIS 的目标减震比，即令 γt,TMIS=γTMD。按照轻量化设计方法，得到使附加TMIS 的单自由度体系达到目标振动控制效果所需的附加质量μt,TMIS，如表2 所示。为衡量TMIS 与TMD 相比对调谐质量的轻量化效果，定义参数 δ如式(28)所示，该参数越大，表示TMIS 对调谐质量的轻量化效果越好。

表1 地震作用下附加TMD 单自由度体系减震比Table 1 Vibration mitigation ratio of SDOF system with TMD under seismic excitation

表2 地震作用下TMIS 的轻量化效果Table 2 Lightweight effect of TMIS under seismic excitation

通过表2 可以得到：在地震作用下，所选取的几组附加TMIS 的单自由度结构在减震比与附加TMD 的结构相同的条件下，所需调谐质量最多降低了40.8%。因此，对单自由度结构附加TMIS，可以在达到与TMD 相同的振动控制目标的条件下，显著降低所需附加调谐质量的大小，即可以实现轻量化振动控制。

4.3 TMIS 的控制频带

本节分别对附加TMD 的单自由度结构、附加TMIS 的单自由度结构的传递函数进行了分析。选择附加质量比μt,TMD为0.01 和0.05 的两种工况，对于TMD 采用优化公式进行设计，对于TMIS 使用基于目标减震比的轻量化设计的结果。在外部激励为地震作用时，如图13 所示，附加TMIS 的结构位移响应传递函数峰值与TMD 相比均有降低。μt,TMD=0.01时，附加TMIS 结构的控制频带比TMD 增加了57.6%；μt,TMD=0.05时控制范围增加了12.6%。

图13 地震作用下附加TMD 与TMIS 的单自由度结构的位移传递函数Fig. 13 Displacement transfer function of SDOF systems with TMD and TMIS under seismic excitation

4.4 时域验证

4.1 节～4.3 节的分析内容均基于频域计算获得，为进一步验证TMIS 的振动控制效果，本节对一个附加TMIS 的单自由度结构模型在时域下进行分析。本节选取的单自由度主结构自振周期为0.9 s，固有阻尼比为0.01。时域分析分别采用白噪声激励和地面运动时程激励，地震作用选取两条天然地震动时程(NW1、NW2)和一条人工地震动时程(AW1)，随后计算无控结构在上述外部激励作用下的动力响应。为与TMIS 进行比较，在单自由度结构中附加TMD，选取附加质量比μt,TMD，采用优化公式设计其它参数。计算附加TMD 的单自由度结构的位移响应，以峰值位移减震比 γU,peak和均方位移减振比 γU,RMS作为衡量减震系统效果的指标，其中峰值位移减震比 γU,peak定义为附加减震系统结构的位移响应峰值与无控结构位移响应峰值之比。对于TMIS，采用第3 节所述的轻量化设计方法，在保障减震效果的同时尽可能降低所需调谐质量的大小。

白噪声激励下，选取两组TMD 附加质量比μt,TMD= 0.02 和0.05，以均方位移响应减震比γU,RMS作为性能目标设计TMIS。附加TMIS 的结构性能如表3 和图14 所示。附加TMIS 的结构所需的附加调谐质量分别降低了43.0%和51.8%，即使用较小的调谐质量对结构均方位移响应进行了有效的控制，实现了调谐质量的轻量化目的。

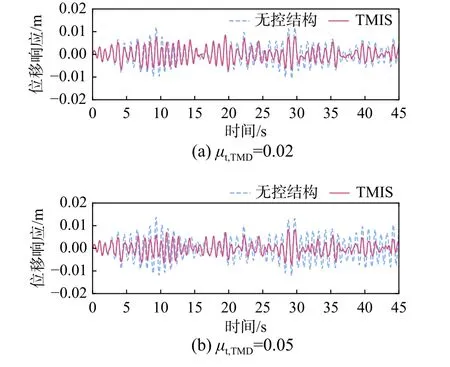
图14 白噪声激励下附加TMIS 单自由度结构的位移响应Fig. 14 Displacement response of SDOF system with TMIS under white noise

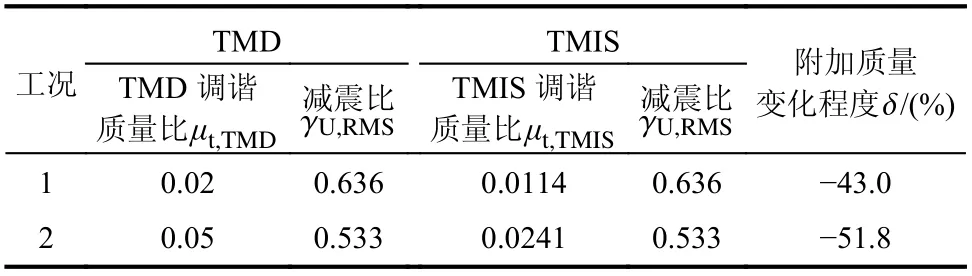
表3 白噪声激励下TMIS 的轻量化控制效果Table 3 Lightweight effect of TMIS under white noise

地震作用下，选取TMD 附加质量比μt,TMD=0.05。经过优化设计后，所需附加质量比μt,TMIS=0.0289，相比TMD 减轻了42.2%，如表4 所示。地震作用下，基于轻量化原则设计的TMIS 可以达到与TMD 相近的减震效果。结果表明：TMIS 在有效控制结构响应的同时显著降低了所需附加的调谐质量。附加TMIS 结构在地震作用下的位移响应如图15 所示，由此可见经过优化设计的TMIS在结构振动控制方面达到了较好的效果。

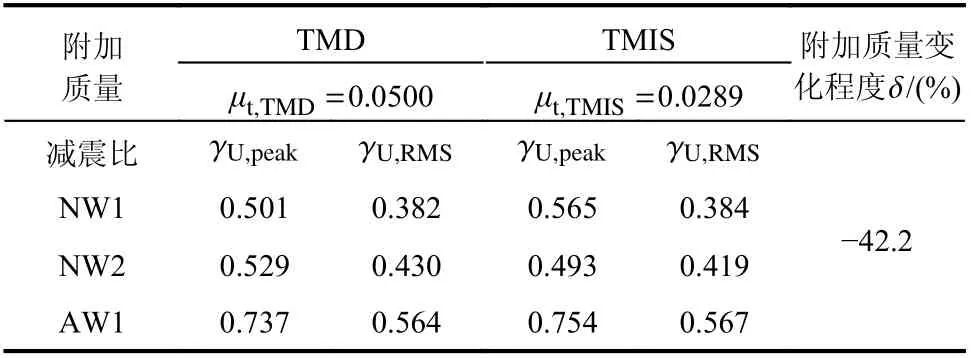
表4 地震作用下TMIS 的轻量化控制效果Table 4 Lightweight effect of TMIS under seismic excitation

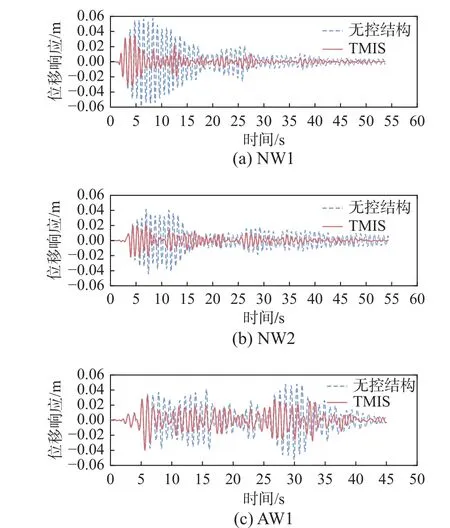
图15 地震作用下附加TMIS 单自由度结构的位移响应Fig. 15 Displacement response of SDOF system with TMIS under seismic excitation

时域验证的结果表明：在具有非平稳特性的地震动时程激励下，TMIS 具有良好的结构振动控制效果，对降低结构的峰值位移响应和均方位移响应都具有作用。与TMD 相比，TMIS 可以实现与TMD 基本相同的控制效果，但TMIS 可以显著降低所需的附加调谐质量大小，实现轻量化的振动控制，在本节使用的单自由度算例中调谐质量轻量化程度达到了42.2%。TMIS 的轻量化效果具有实际应用意义，可以使用较小的附加质量达到良好的控制效果，实现更为经济高效的结构振动控制。

5 风荷载作用下TMIS 轻量化控制

5.1 基于单自由度体系的TMIS 轻量化风振控制理论研究

5.1.1 TMIS 结构振动控制效果

本节比较了附加TMD 的单自由度体系和附加非接地式TMIS 的单自由度体系在风荷载作用下的性能，同样以减振比 γ衡量减振系统的振动控制效果。对于风荷载，采用与地震作用理论研究相同的研究方法，考虑到风致振动往往对结构舒适度造成影响，因此采用衡量结构舒适度常采用的加速度响应作为结构性能指标。在本节的单自由度体系理论研究中，以主结构均方加速度响应减振比 γA作为评价指标；在多自由度体系中，一般以结构顶部加速度响应指标作为结构性能评价的依据。

对于附加TMD 与TMIS 的参数设计，依旧采用第4 节的方法，设计目标为达到最小的减振比。按照上述方法设计减振系统所得的振动控制效果如图16 所示，对应的TMIS 设计参数如图17所示。从图16 中可以发现，风荷载作用下TMIS可以进一步降低结构动力响应，为减振系统轻量化带来可能，在满足结构性能需求的前提下可以进一步优化所需的调谐质量的大小。

图16 风荷载作用下附加TMD 和TMIS单自由度结构的减振比Fig. 16 Vibration mitigation ratio of SDOF systems with TMD and TMIS under wind load

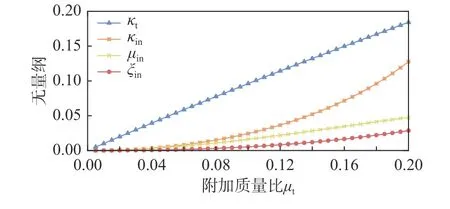
图17 风荷载作用下各附加质量比时的TMIS 优化参数Fig. 17 Optimal parameters of TMIS with different additional mass ratio under wind load

5.1.2 TMIS 的轻量化振动控制效果

本节对比了不同的减震比需求下，TMIS 对于调谐质量系统的轻量化作用。取10 组调谐质量比作为附加TMD 的调谐质量μt,TMD，使用TMD 优化设计公式计算其余设计参数，得到风荷载作用下附加TMD 单自由度体系均方加速度减振比如表5所示。随后，按照轻量化设计方法，得到使附加TMIS 的单自由度体系达到目标振动控制效果所需的附加质量μt,TMIS，如表6 所示。

表5 风荷载作用下附加TMD 单自由度体系减振比Table 5 Vibration mitigation ratio of SDOF system with TMD under wind load

表6 风荷载作用下TMIS 的轻量化控制效果Table 6 Lightweight effect of TMIS under wind load

风荷载作用时，所选取的几组附加TMIS 的单自由度结构在减震比与附加TMD 的结构相同的条件下，所需调谐质量最多降低了42.7%，即TMIS可以在达到与TMD 相同的振动控制目标的条件下，显著降低所需调谐质量的大小。通过单自由度的理论分析可以发现，在地震作用和风荷载两种外部激励下，TMIS 均可以实现减振系统的轻量化。调谐质量的减轻意味着所使用的结构振动控制系统更加经济、高效，在实际应用中具有优势。

5.1.3 TMIS 的控制频带

风荷载作用下对附加TMD 和TMIS 的单自由度体系传递函数的分析结果如图18 所示，附加TMIS的结构位移响应传递函数峰值与TMD 相比均有降低。μt,TMD=0.01时，附加TMIS 结构的控制频带比TMD 增加了20%；μt,TMD=0.05时控制范围增加了23.5%。上述结果表明：在风荷载和地震作用下TMIS 在振动控制频带上有所拓宽。

图18 风荷载作用下附加TMD 与TMIS 单自由度结构的加速度传递函数Fig. 18 Acceleration transfer function of SDOF systems with TMD and TMIS under wind load

5.2 风荷载作用下基于多自由度结构的TMIS 振动控制轻量化

在超高层结构中使用非接地式TMIS 进行风振控制，多自由度建筑结构体系示意图如图19 所示。采用一经典的600 m 级超高层模型作为研究对象，建立精细化有限元模型，进行结构特定楼层加速度响应研究。所使用的风荷载分别为1 年、10 年、50 年、100 年和500 年回归期，沿80°和270°方向作用于结构。该超高层结构采用调谐质量为1000 t 的TMD 进行振动控制，本研究采用3.1 节所述的基于性能需求的轻量化优化设计方法设计TMIS，在相同减振比的控制条件下，可将所需调谐质量降低为600 t，轻量化程度达到40%。采用时程分析验证了TMIS 的控制效果，如表7 所示，结果表明：轻量化设计的TMIS 可以达到与TMD 相同甚至更优的控制效果。

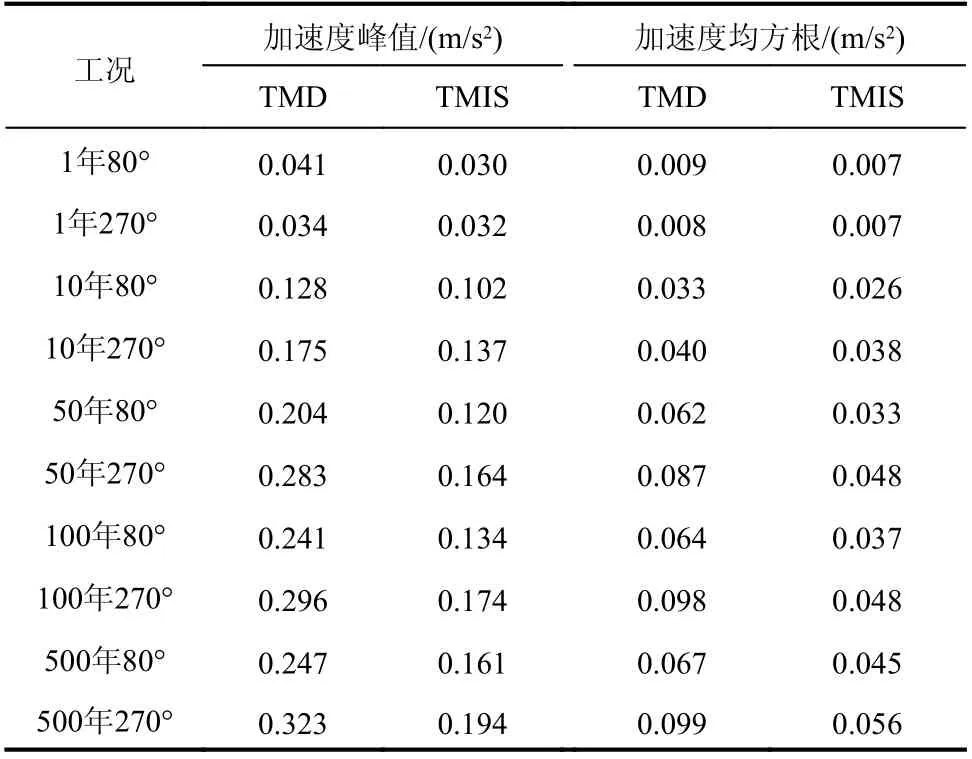
表7 不同重现期的风荷载工况下TMIS(600 t)和TMD(1000 t)加速度响应对比Table 7 Acceleration response of structures with TMD(1000 t) and TMIS (600 t) under wind load

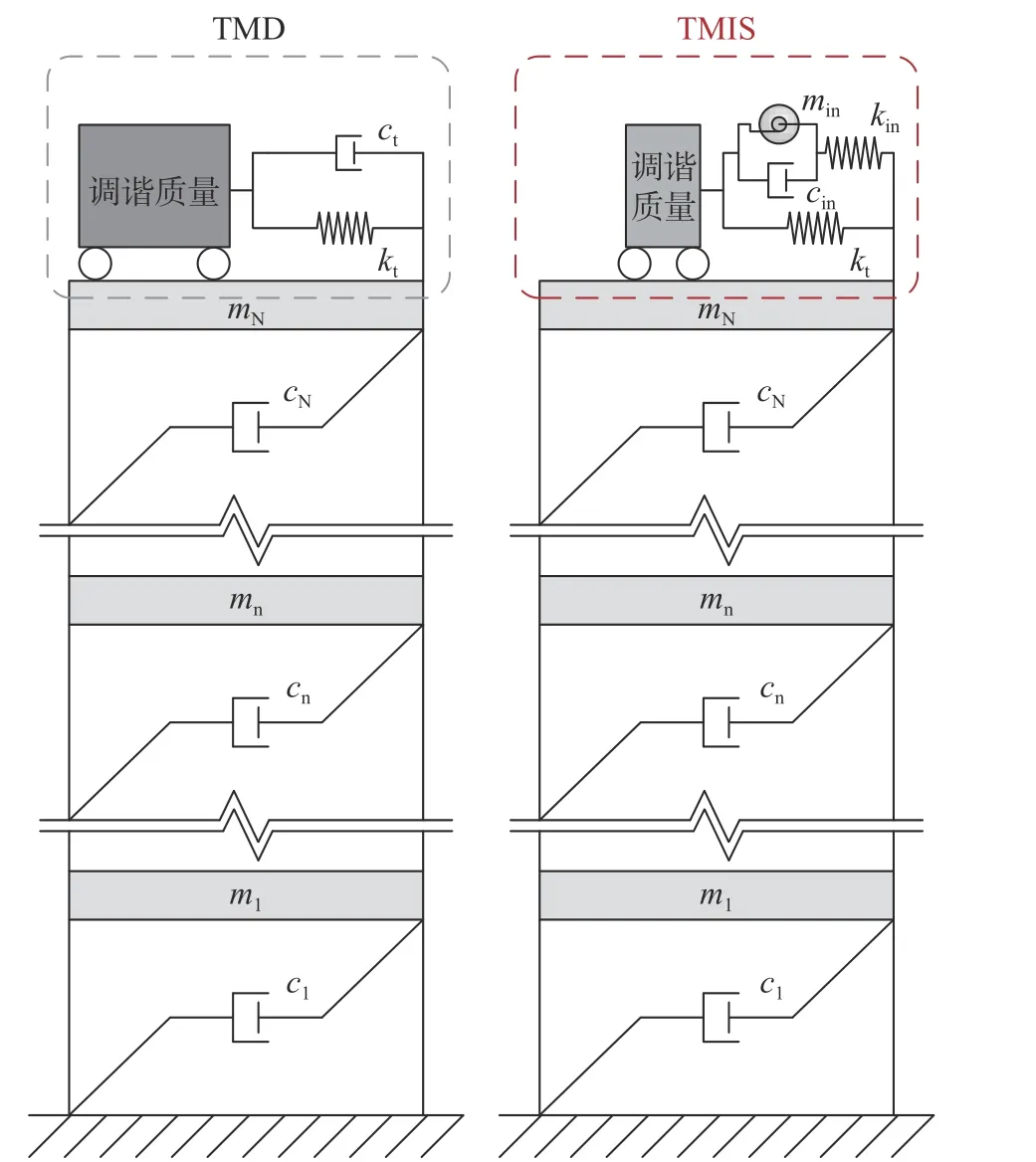
图19 多自由度建筑结构附加减振装置示意图Fig. 19 MDOF structures with different vibration control devices

6 人致激励作用下TMIS 轻量化控制

本节以一个楼板结构为例研究人致激励下TMIS的结构振动控制。当人员活动产生的振动频率与楼板自振频率接近时可能造成共振现象，TMIS可以抑制人致激励下楼板结构的振动响应。以并联型惯容子系统为例，附加TMIS 的楼板结构如图20 所示。将该结构与附加TMD 的楼板结构进行对比研究，其中TMD 的调谐质量μt,TMD分别取为0.1、0.3 和0.5，TMD 其余力学元件参数由经典定点理论[4]进行设计。对于TMIS 的设计，同样采用3.1 节所述的轻量化设计方法，将附加TMD结构的减振比作为设计TMIS 的目标减振比，最小化TMIS 所需的调谐质量大小。

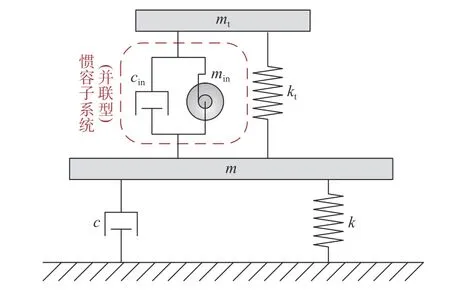
图20 附加TMIS 的楼板结构示意图Fig. 20 Floor structure with TMIS

人致激励下附加TMD 与TMIS 对比研究结果如表8 所示。在达到相同的舒适度控制目标的情况下，TMIS 所需调谐质量最多降低了71.8%；人致激励下附加TMIS 的楼板结构的加速度响应时程如图21 所示，表明TMIS 可以使用较小的附加质量有效控制人致激励下楼板的振动响应。

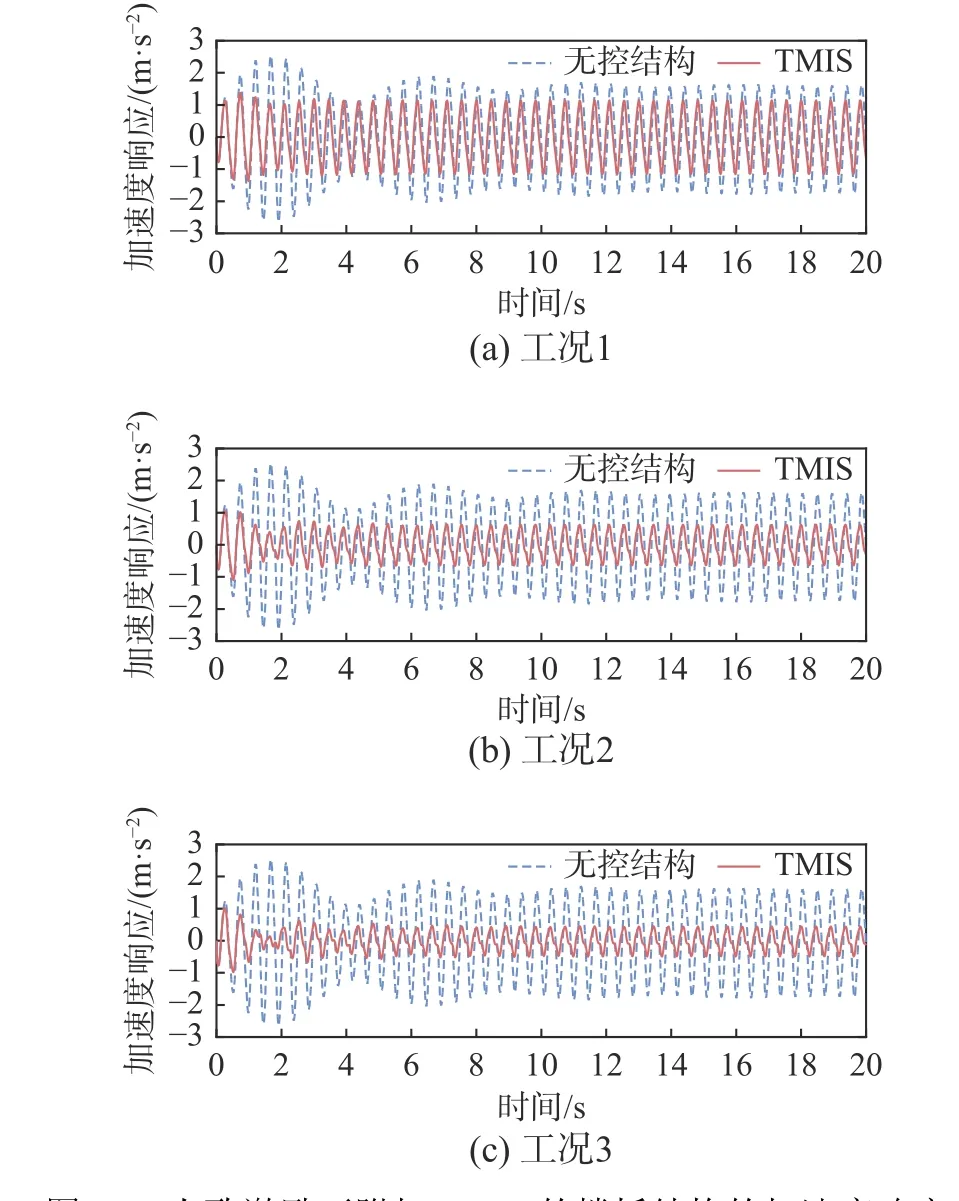
图21 人致激励下附加TMIS 的楼板结构的加速度响应Fig. 21 Acceleration response of floor structure with TMIS under human-induced excitation

表8 人致激励下TMIS 的轻量化控制效果Table 8 Lightweight effect of TMIS under human-induced excitation

7 结论

目前，得到广泛应用的调谐质量减震(振)系统TMD 由于需要较大的附加质量，在实际使用中具有一些不足。本文聚焦广义调谐质量惯容系统TMIS，该系统以具有轻量化特性的惯容系统为特征，内部拓扑连接形式可以多样化。提出基于性能需求的优化设计方法设计TMIS 的参数，在地震作用、风荷载与人致激励三种典型激励下，通过与TMD 的对比研究说明了TMIS 的轻量化减振控制优势，并通过多自由度结构案例与动力时程分析验证TMIS 的振动控制效果和特性。本文的研究得到以下结论：

(1)在地震作用、风荷载及人致激励这三种典型激励下，附加TMIS 结构的动力响应得到了明显降低，表明TMIS 能有效实现结构振动控制的性能目标；

(2)基于结构性能需求的TMIS 参数设计方法以减震(振)比作为衡量结构性能的指标，以调谐质量的轻量化为优化目标，可以在达到目标性能需求的同时充分发挥TMIS 在结构振动控制上的优势；

(3)对比研究表明：TMIS 在达到与经典TMD相同性能目标的情况下，可以显著降低所需的附加调谐质量，实现轻量化调谐减振。这一特点可以提供轻量化、小型化的绿色高效振动控制装置，减少调谐减振系统占用的空间，降低成本，使结构调谐减振控制更加经济；

(4)本文基于单自由度和多自由度结构算例的研究说明TMIS 在结构振动控制领域具有轻量化减振控制特性，且适用于不同典型激励工况。TMIS轻量化减振的优势使得TMIS 在实际建筑结构，特别是大跨空间结构、高层、超高层结构中具有应用前景；

(5)本文以两种力学拓扑形式的TMIS 为例进行研究。相较于以往得到广泛研究的接地式惯容系统，TMIS 不受接地要求限制，保留了惯容的两端点惯性特性，可以发挥惯容本身的调谐和耗能增效特性，因而更加灵活，在实际工程应用中具有潜力。

(6)广义TMIS 并非只有本文所涉及的形式，针对不同应用场景，在具有不同需求的结构体系中应用不同拓扑连接形式的TMIS 进行特定或综合工况下的振动控制还需要进一步研究。