型钢混凝土深梁受剪性能及承载能力研究

陈步青，曾 磊，刘昌俊，莫金旭

(1. 长江大学城市建设学院，荆州 434023；2. 广州大学土木工程学院，广州 510003)

型钢混凝土深梁具有承载力高、刚度大、耐久性好等优点，现被广泛应用于结构转换层、地下结构、桥梁结构中[1-3]。由于不能忽略剪切变形产生的影响，型钢混凝土深梁的受剪机理较为复杂，现行设计规范大多基于强度叠加的方法来进行型钢混凝土构件的受剪承载力设计[4-15]。但显然型钢部分与钢筋混凝土部分的抗剪承载力不能同时达到峰值，上述方法将会高估构件的受剪承载力。

由Vecchio 和Collins[16]提出的修正压力场理论考虑了开裂后混凝土残余承载力对构件受剪承载力的作用，采用平均应力和平均应变建立起钢筋和混凝土组合单元的平衡方程、变形协调方程以及本构方程，计算受平面内剪应力和轴向应力作用下的钢筋混凝土单元的响应，能合理阐述钢筋混凝土构件的受剪机理，已经被美国、加拿大等[17 - 18]国家的混凝土规范所采用。朱庆伟等[19]、柯晓军等[20]和朱孔峰等[21]学者采用修正压力场理论对型钢混凝土柱、钢管混凝土组合结构、钢筋混凝土深梁的受剪承载力进行了研究，表明基于修正压力场理论的受剪承载力计算公式精度较高。

本文以剪跨比、型钢截面高度比、翼缘宽度比为影响因素，对7 个型钢混凝土深梁试件进行了受剪性能试验，揭示了集中荷载作用下的破坏模式、承载能力以及变形特征，基于修正压力场理论提出了受剪承载力计算模型，并与本文及已有文献中的数据进行了对比验证。

1 试验概况

1.1 试件设计

以不同剪跨比、型钢截面高度比(内置型钢截面高度与梁截面高度比值)、翼缘宽度比(型钢翼缘宽度和梁截面宽度比值)为设计参数，按照现行规范设计了7 个型钢混凝土深梁试件，各试件的详细参数如表1 所示。试件的截面尺寸及布置如图1 所示。所有试件均采用C40 商品混凝土一次浇筑而成，混凝土立方体的抗压强度实测值为42.1 MPa，纵筋采用直径18 mm HRB335 级螺纹钢筋，箍筋采用直径6 mm HPB300 级光圆钢筋，内置H 型钢采用Q235 级钢板焊接成型。钢材的力学性能如表2 所示。

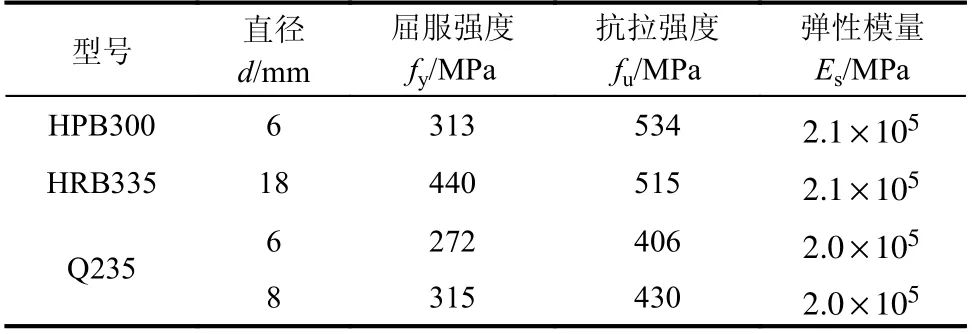
表2 钢材力学性能参数Table 2 Material properties of steel

图1 试件截面尺寸及配筋图 /mmFig. 1 Section dimension and reinforcement

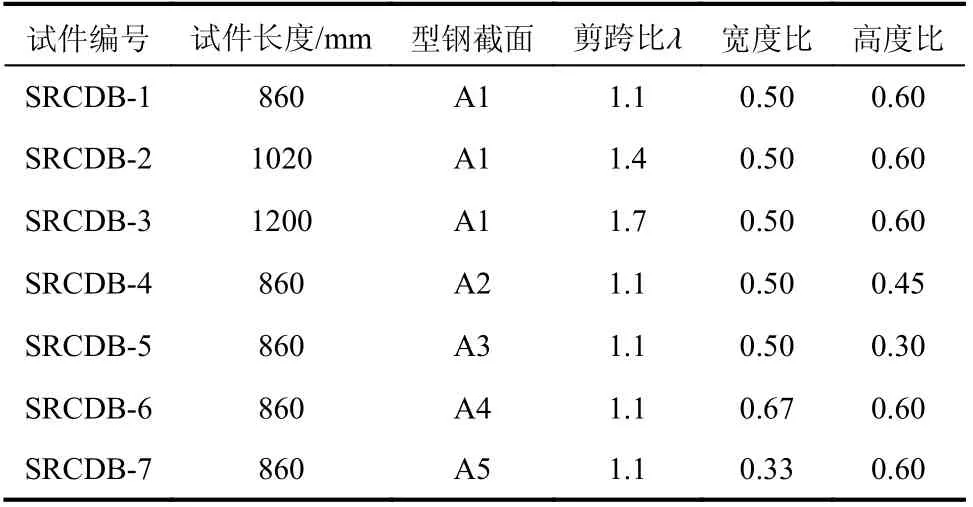
表1 试件设计参数Table 1 Design parameters of specimens

1.2 试验装置和加载制度

试件两端简支，采用伺服液压控制作动器进行跨中单点单调加载。荷载通过位移控制模式以0.5 mm/min 的加载速率分阶段施加，加载至极限荷载的0.85 倍时停止加载。试验过程中实时记录各加载阶段试件的裂缝、变形、应变等响应，试件的加载装置和测试仪器如图2 所示。在加载点放置刚性垫板，在试件跨中、支座处分别布置位移计和百分表测量跨中位移和支座转角，在跨中加载点至支座区域沿试件高度布置应变片测量加载过程中混凝土、型钢、钢筋、箍筋等部分的应变情况。

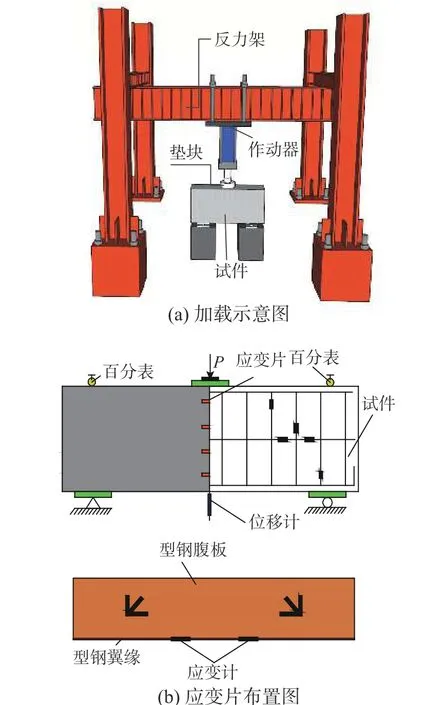
图2 试验加载示意图Fig. 2 Schematic diagram of test setup

2 试验结果及分析

研究过程中主要从型钢混凝土深梁的破坏形态、荷载-位移响应、应变分布、开裂行为等方面对结果进行讨论。

2.1 破坏形态

试件的破坏形态以及试验结果见图3 和表3，剪跨比是型钢混凝土深梁破坏形态的主要影响因素。试件的破坏形态主要为斜压破坏和剪压破坏。

表3 特征点荷载及位移Table 3 Load and displacement at characteristic points

1)斜压破坏

剪跨比较小时( λ =1.1)的试件发生斜压破坏，表现为加载点至支座区域的混凝土破碎。以SRCDB-6 为例，其破坏过程为：当荷载加载至113 kN (0.14Pu)时，跨中截面下部开始出现竖向裂缝，宽度为0.025 mm，并随着荷载的增加延伸至约2/3 梁高处；当加载至171 kN (0.21Pu)时，剪跨区腹部出现斜裂缝，数量也随着荷载的增加逐渐增多，最终形成了一条由加载点指向支座的贯通斜裂缝，与梁轴线的夹角约为40°；当加载至峰值荷载时，斜裂缝宽度逐渐增加，最大达到1.5 mm，此时斜压区混凝土被压碎脱落，形成若干斜向混凝土短柱，试件破坏。

2)剪压破坏

剪跨比较大时( λ =1.4 ～1.7)试件发生剪压破坏。表现为在斜裂缝出现后，荷载仍有明显的提高，临界斜裂缝上端集中于荷载作用点附近。以SRCDB-3 为例，其破坏过程为：当荷载加载至72 kN (0.13Pu)时，因弯曲应力的作用，在梁的跨中部位出现一条长约50 mm 的裂缝，并随着荷载的增加，裂缝沿着梁向上发展并出现数条出齐短裂缝；当荷载加载至143 kN (0.23Pu)时，剪跨段开始出现斜裂缝，随着荷载继续增加，在跨中截面处弯曲裂缝发展变缓，新的竖向裂缝几乎不再出现，而剪跨段的斜裂缝发展迅速，形成数条连接加载点到支座方向的斜裂缝；当加载至峰值荷载时，斜裂缝宽度突然增加，少数混凝土从表面剥离，承载力缓慢下降，试件破坏。

2.2 荷载-位移曲线

图4 为各试件荷载-位移曲线。通过试件表面出现的第一条斜裂缝确定开裂荷载Pcr及开裂位移Δcr；荷载-位移曲线上的峰值荷载对应的荷载和位移分别为Pm和Δm；荷载下降至85%值时的点定义为破坏点，对应的荷载和位移分别为Pu和Δu；采用“等效能量法”来确定试件的屈服点，对应的荷载和位移分别为Py和Δy，以极限位移Δu与屈服位移Δy之比来确定试件的位移延性系数。表3为试件加载过程中特征点的荷载及位移，由图4与表3 对比分析可知：

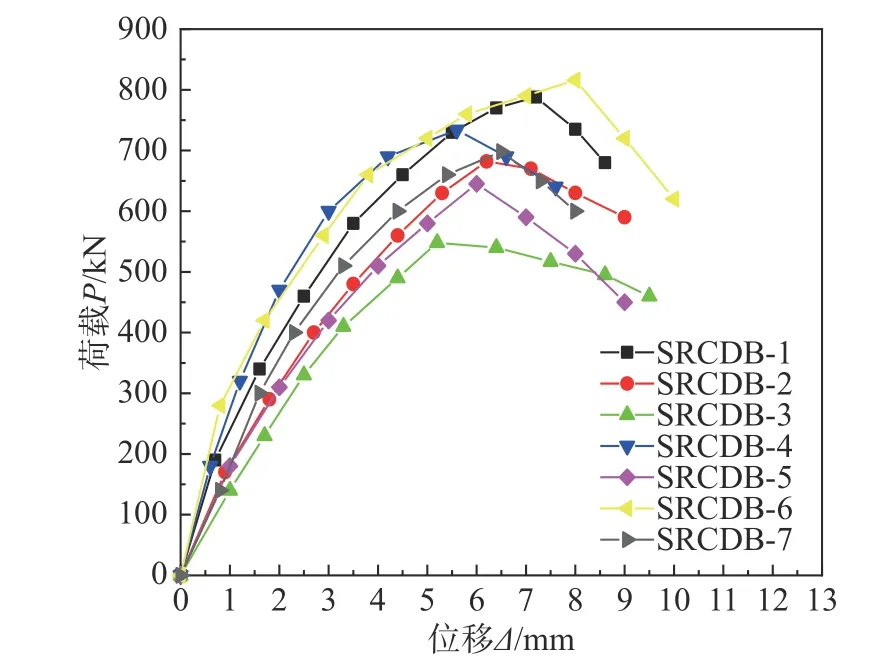
图4 荷载-位移曲线Fig. 4 Load-displacement curve

1)加载初期，混凝土受拉区未开裂时，试件处于弹性状态，荷载-位移曲线的斜率呈线性变化；达到屈服荷载后，曲线的斜率开始下降，荷载的增速变缓，刚度退化；当试件达到峰值荷载后，承载力下降速度较快。

2)剪跨比对试件的承载力和位移延性影响较大，剪跨比大的试件承载能力低，但位移延性系数大。

3)型钢截面布置对型钢混凝土深梁极限承载力影响较大。结果表明：翼缘宽度比较大时，试件的承载能力更好，随着宽度比的增加，型钢对混凝土的约束能力增强，进而提高了试件的极限承载力。如试件SRCDB-1 与试件SRCDB-7 相比，宽度比增加了34%，极限承载力提高约17%；高度比较大时，试件承载能力更好，对比试件SRCDB-4与试件SRCDB-5 高度比增加15%，极限承载力提高约18%。

2.3 截面应变分布

2.3.1 混凝土应变

通过跨中布置的应变片实测加载过程中沿截面高度不同位置混凝土表面的应变分布，图5 为发生斜压破坏和剪切破坏的2 个试件在不同荷载情况下的应变分布情况，可以看出：试件在弹性阶段时，通过应变片测得混凝土应变较小，且变化规律符合平截面假定，中性轴的位置大约在截面高度的3/5 处，随着裂缝的开展，中性轴的位置向上偏离。当竖向荷载加载至极限荷载的35%左右时，试件进入弹塑性阶段，混凝土应变较大，变化规律不再满足平截面假定。在发生剪切破坏构件的混凝土所能达到的应变要大于发生斜压破坏的构件；试件发生斜压破坏时，加载后期混凝土的应变剧烈增长，反映了剪切破坏时试件具有更好的变形能力。

图5 沿截面高度应变分布Fig. 5 Strain distribution along cross-section

2.3.2 型钢腹板应变

型钢腹板处于斜向拉、压二维应力场中，型钢腹板的受力可视为二向平面应力状态下的应变问题。通过型钢腹板测点位置应变花沿三个方向的线应变求得各测点处的主应变及主应变方向。图6 为试验各阶段弯剪段型钢腹板的主应变值以及主应变方向。试验中弯剪段型钢腹板的应变变化情况与腹板的实际破坏现象较为吻合。在加载初期，型钢腹板的应变值较小，当试验值观察到弯剪段出现第一条斜裂缝时，型钢腹板应变突增。另外试件初裂时，型钢腹板未屈服，随着荷载的增加，应变有较大幅度的提升，当试件屈服时，部分型钢腹板开始屈服，主应变方向约为45°方向。随后试件破坏程度进一步加剧，型钢腹板的变形增大，型钢腹板应变急剧增加，钢材进入强化阶段。此外观察得到，型钢主拉应力总是大于主压应力。

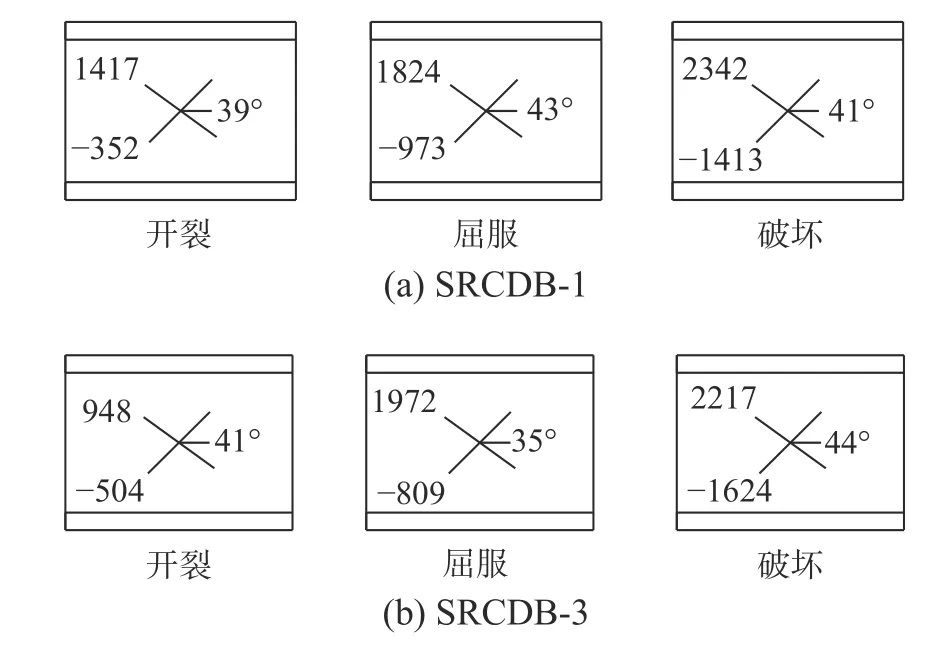
图6 型钢腹板主应变及其方向Fig. 6 Principal Strain and direction of web steel

3 受剪承载力计算

修正压力场理论采用莫尔圆分析试件受剪开裂后膜单元的应力-应变情况，认定剪应力与正应力均匀分布在膜单元内，并根据应力平衡条件、变形协调条件、材料本构关系及裂缝局部应力条件，列出理论模型的基本公式。本文基于修正压力场理论，考虑剪跨比对斜裂缝倾角的影响规律以及型钢翼缘宽度对构件受剪承载力的作用，提出型钢混凝土深梁受剪承载力计算模型。

3.1 修正压力场模型

3.1.1 应力平衡条件

型钢混凝土深梁中剪力主要是由型钢腹板及翼缘承担，纵筋主要承受纵向拉力，假定纵向钢筋部分的剪应力为0，则有：

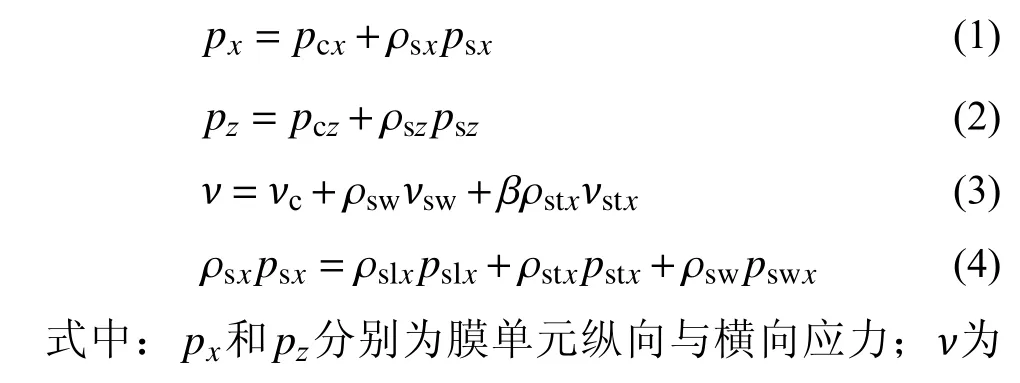
3.1.2 变形协调条件

图7 平均应力莫尔圆Fig. 7 Mohr's circle of average concrete stresses

图8 开裂后混凝土薄膜单元平均应变莫尔圆Fig. 8 Mean strain Mohr circle for cracked concrete membrane element

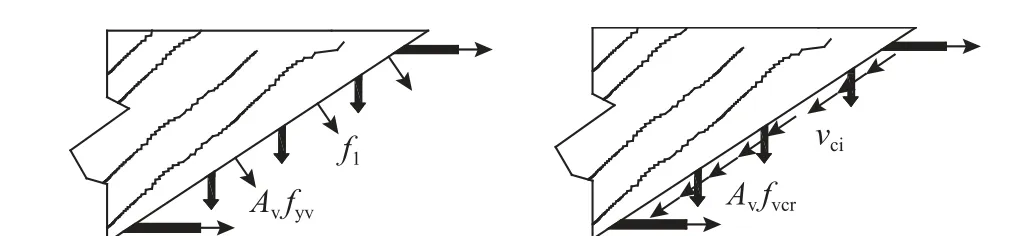
图9 裂缝处剪力传递图Fig. 9 Force transmission across crack

3.2 材料本构模型

3.3 受剪承载力分析

图10 为截面平衡关系，箍筋处竖向力平衡公式为：

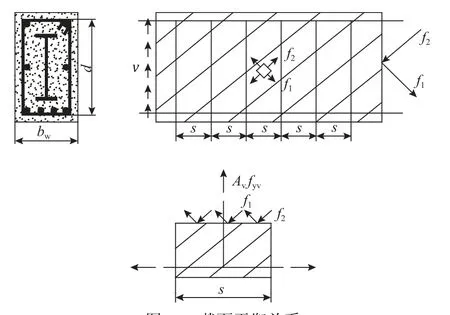
图10 截面平衡关系Fig. 10 Equilibrium condition for section

3.4 受剪承载力迭代计算

3.3 节分析已得出型钢混凝土深梁的应力平衡、变形协调、本构方程以及裂缝处和裂缝间平衡的基本公式，通过这些公式利用迭代方法可以计算型钢混凝土深梁的受剪承载力。计算步骤如图11 所示。

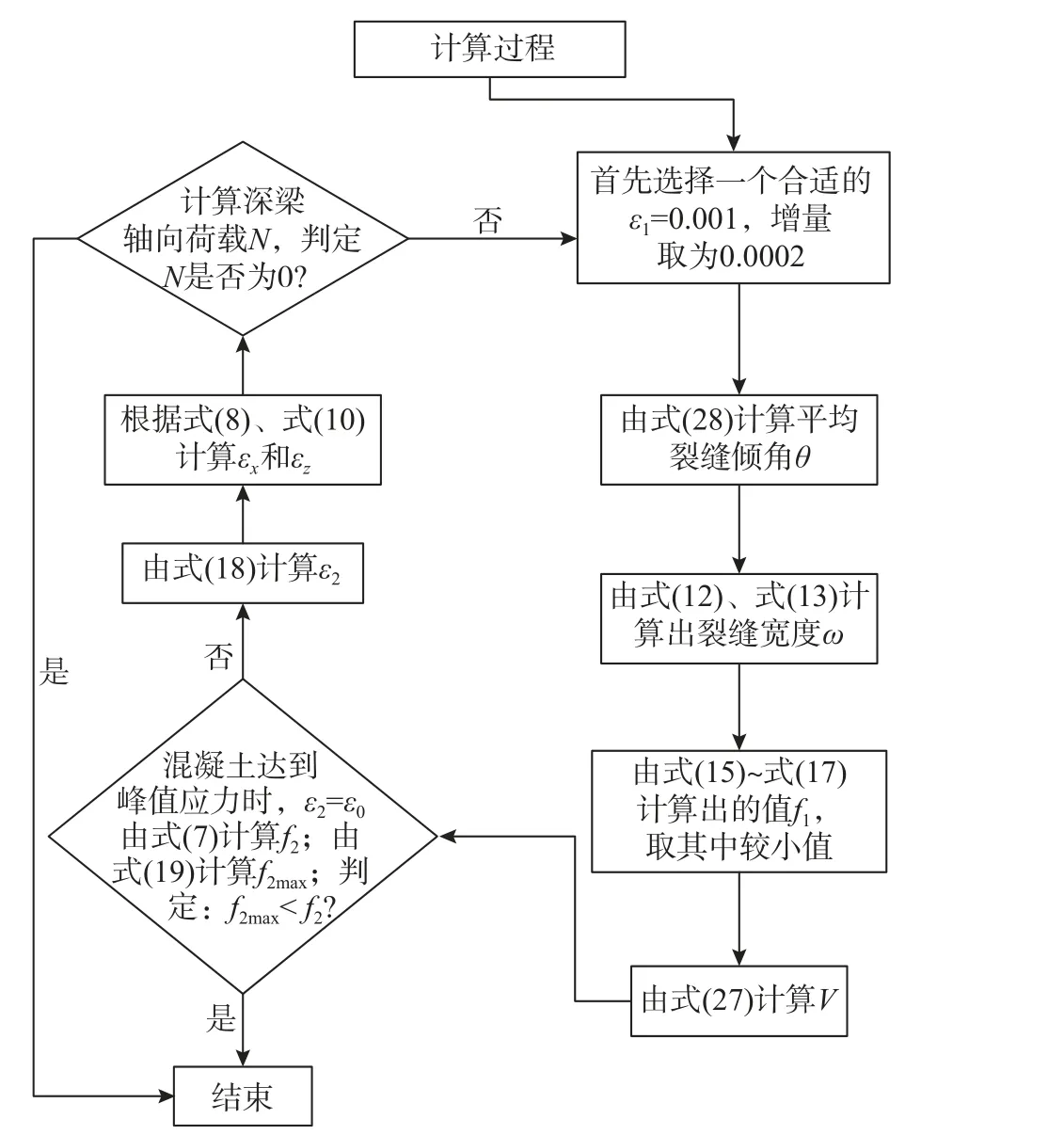
图11 计算流程Fig. 11 Calculation flow

4 模型分析结果与验证

为了验证上述计算模型的准确性，利用本文和已有文献[22, 26 - 31]共32 根型钢混凝深梁采用《组合结构设计规范》(JGJ 138-2016)[4]、《钢骨混凝土结构技术规程》(YB 9082-2006)[6]及本文计算流程计算受剪承载力，抗剪承载力为集中荷载的一半，并与试验结果进行对比。试件基于修正压力场理论计算模型得到的受剪承载力迭代计算值为VMCFT；试验实测极限承载力为Ve。

计算结果见表4 和图12，分析可得：

图12 不同理论预测的受剪承载力Fig. 12 Bearing capacity predicted by different modulus

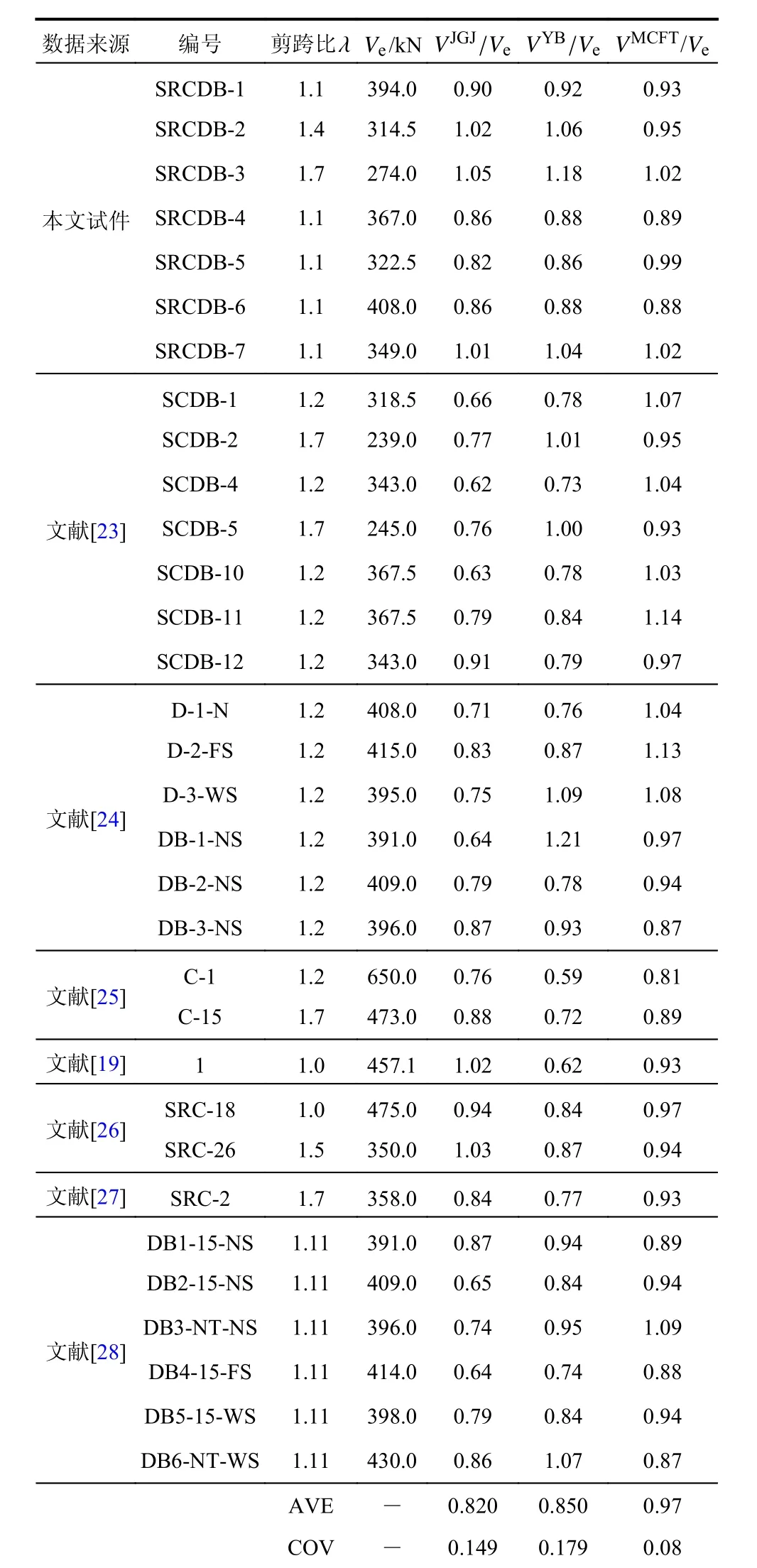
表4 受剪承载力计算结果与试验结果对比Table 4 Comparison of predicted and experiment results

1)采用JGJ 138-2016[4]计算的型钢混凝土深梁的受剪承载力偏小，与试验值比值的平均值为0.82，其变异系数为0.149，结果偏于安全。采用YB 9082-2006[6]计算的型钢混凝土深梁的受剪承载力与试验值比值的平均值为0.85，变异系数为0.179，两者离散性均较大。

2)采用本文推导的计算模型计算型钢混凝土深梁承载力，与试验值比值的平均值为0.97，变异系数为0.08，离散型较小。研究表明[14]：型钢翼缘宽度较大时，型钢对混凝土有着很好的约束能力。因此，本文合理考虑型钢翼缘的抗剪作用的计算结果与试验值吻合较好。

5 结论

通过7 个试件的抗剪性能试验，本文研究了在不同剪跨比、型钢翼缘宽度比以及不同型钢腹板高度的情况下，型钢混凝土深梁的抗剪性能，获得了以下主要结论，可为工程推广应用提供参考。

(1)型钢混凝土深梁根据剪跨比的不同，呈现两种不同的破坏形态：当剪跨比 λ≤1.1 时，发生斜压破坏；当剪跨比 1.1 ＜λ≤1.7时，发生剪压破坏。随着剪跨比的增加，型钢混凝土深梁的受剪承载力呈下降趋势。

(2)随着翼缘宽度比的增加，型钢混凝土深梁的抗剪承载能力以及延性均有所提高；随着高度比的增加，试件的抗剪承载能力有明显提升。

(3)本文建立的基于修正压力场理论的型钢混凝土深梁计算模型合理考虑了裂缝间混凝土骨料的咬合力和摩擦力以及型钢翼缘宽度对构件受剪承载力的作用，并通过关键参数θ 以及 εx来反映了剪跨比以及配箍对深梁受剪承载力的影响。该模型预测的型钢混凝土深梁受剪极限承载力与试验值较为吻合，变异系数较小，优于现行规范。本文提出的受剪模型可为建立型钢混凝土深梁受剪承载力设计规范公式提供理论基础。