基于应变模态响应重构的损伤识别方法

邹云峰，卢玄东，阳劲松，何旭辉

(1. 中南大学土木工程学院，湖南，长沙 410075；2. 中南大学交通运输工程学院，湖南，长沙 410075；3. 轨道交通工程结构防灾减灾湖南省重点实验室，湖南，长沙 410075)

土木结构的性能在其运营阶段会随着时间推移而下降，从而影响结构的安全性和耐久性，土木结构健康监测技术一直是国内外的研究热点[1-2]。土木结构损伤形式多样、损伤位置隐蔽，由于土木结构形式复杂、尺度大等特点，很难对土木结构损伤进行准确识别，若放任损伤不断发展，很有可能导致重大安全事故，因此开展土木结构损伤识别研究具有重要意义。

现有结构损伤识别方法的基本原理是，损伤会导致结构物理特性的变化，该变化会反映在实际测量的结构动态响应中，通过分析结构动态响应的变化实现损伤识别[3-5]。损伤识别方法可大致分为3 种：一是频域方法[6-8]，主要识别参数包括频率、振型和曲率模态等，该方法需要在频域上识别模态参数，具有一定的复杂性且难以保证计算精度；二是时域方法，如基于响应灵敏度的识别方法[9-10]，此种方法需要通过外部激励和结构动态响应的关系来进行损伤识别，具有数据量充足、识别精度高的特点，但需要准确的外荷载信息，而实际结构的外荷载通常难以获取；三是时频域方法，如基于小波包灵敏度的识别方法[11-12]，此种方法同样需要获取外荷载信息，而且在时频域上进行的正向运算和反向运算，其计算效率较低，过程繁复。

针对以上问题，本文将动态响应重构方法引入损伤识别中，通过已有的测量信息去获取全局的结构动态响应，从而解决需要已知外部载荷的局限。Ribeiro 等[13]针对多自由度系统提出一种基于广义传递矩阵的响应重构法，在频域内建立两组响应的传递矩阵，进而实现响应待测点的重构工作；Law 等[14-16]基于频响函数将上述位移传递率推广至加速度传递率，完成了全模型或模型子结构上的响应重构。He 等[17-19]提出一种基于经验模态分解的时域响应重构方法，该方法通过结构模态特性构建传递矩阵，结合经验模态分解法和模态叠加法得到未安装传感器位置的动力响应，相对于频域重构方法，该方法具有更高的计算效率。目前，时域重构方法仅用于无损伤结构的响应重构，若结构出现损伤而引起结构参数改变，使用原本的传递函数重构得到的响应必然与真实响应存在差别，通过利用这种差异性结合有限元更新方法可以实现对土木结构的损伤识别[20-21]。

本文结合基于经验模态分解的响应重构方法，提出一种基于应变模态响应重构的损伤识别方法。该方法根据传感器采集的响应信息直接分解得到的模态响应和使用无损伤模型的应变模态重构得到的模态响应的差异作为有限元模型修正的依据，通过应变模态比值构建的传递率的灵敏度矩阵进行迭代运算，求得损伤位置及损伤程度。由于该方法不需要获取外部激励信息，且在时域中进行，无需进行频域的相关计算和时频域转换，关键信息的获取方便快捷。最后，通过连续梁的单一损伤识别和多损伤识别验证了该方法的正确性和有效性，并讨论了不同等级的测量噪声和模态阶次的选取对识别结果的影响。

1 基于应变模态响应重构的损伤识别理论推导

1.1 基于经验模态分解的应变重构方法

使用经验模态分解(EMD)法处理时域信号的方法分解传感器的测量响应，可以将测量响应近似表示为：

1.2 基于应变模态响应重构的有限元模型修正

将损伤识别问题表述为使实际结构和有限元模型之间有关结构特性的信息差异最小值问题：

基于应变模态响应重构的损伤识别方法，其基本流程如图1 所示。

图1 损伤识别流程图Fig. 1 Flowchart of damage identification method

2 数值模拟分析

2.1 连续梁损伤识别

通过连续梁仿真案例以验证本文提出的基于应变模态响应重构的损伤识别方法。用于数值模拟的连续梁有限元模型如图2 所示，该连续梁弹性模量为210 GPa，密度为7850 kg/m3，长、宽、高分别为3 m、0.06 m、0.03 m。采用ANSYS 建立有限元模型，单元类型为beam3 单元，共有31 个节点，30 个单元，每个单元长为0.1 m，从左往右分别给节点编号1～31，单元编号1～30。无损伤状态下连续梁的前5 阶自振频率分别为20.85 Hz、32.48 Hz、83.38 Hz、105.32 Hz、187.61 Hz。对该连续梁模型设置多组损伤工况，损伤工况主要考虑连续梁容易发生损伤的部位，如跨中和支座附近部位，以此来验证所提出的损伤识别方法的可行性，损伤工况的设置如表1 所示。

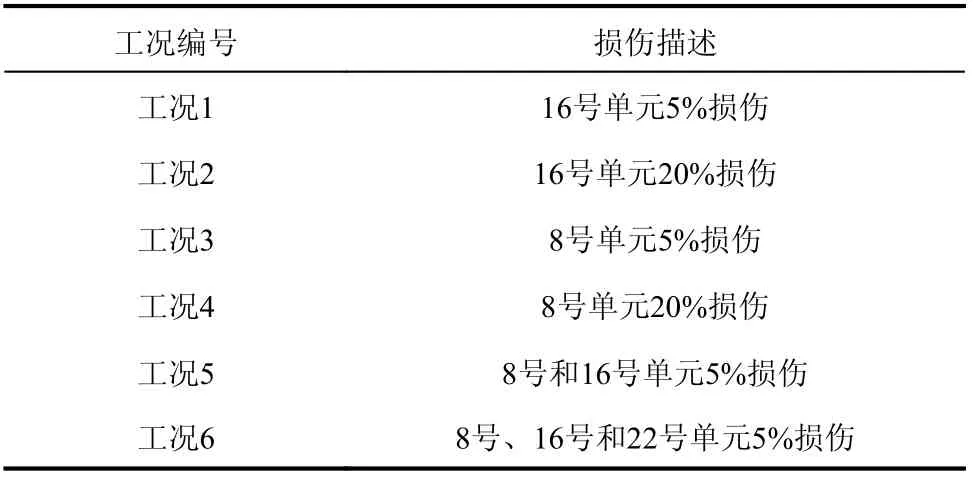
表1 损伤工况Table 1 Damage condition

图2 连续梁模型Fig. 2 Model of continuous beam

由理论推导可知，本文损伤识别方法与外界激励无关，将幅值在一定范围内的竖向冲击荷载施加于连续梁的8 号节点上。应变片布置在每个单元上部中心位置，采样频率为1 kHz，如图2 所示。选取结构自由振动期间1 s 的响应信号，提取一阶模态响应并根据式(9)～式(11)得到差异向量。在这里需要注意的是，对于多组应变片采集的数据，可以有不同种重构方式组合，在该数值模拟中，经过多次对比发现，重构方式组合只会在存在噪声的情况下对识别结果产生影响，且该影响较小，在此不予讨论。

为了提高识别精度，迭代求解加入了自适应Tikhonov 正则化方法[22]，识别结果如图3 所示。

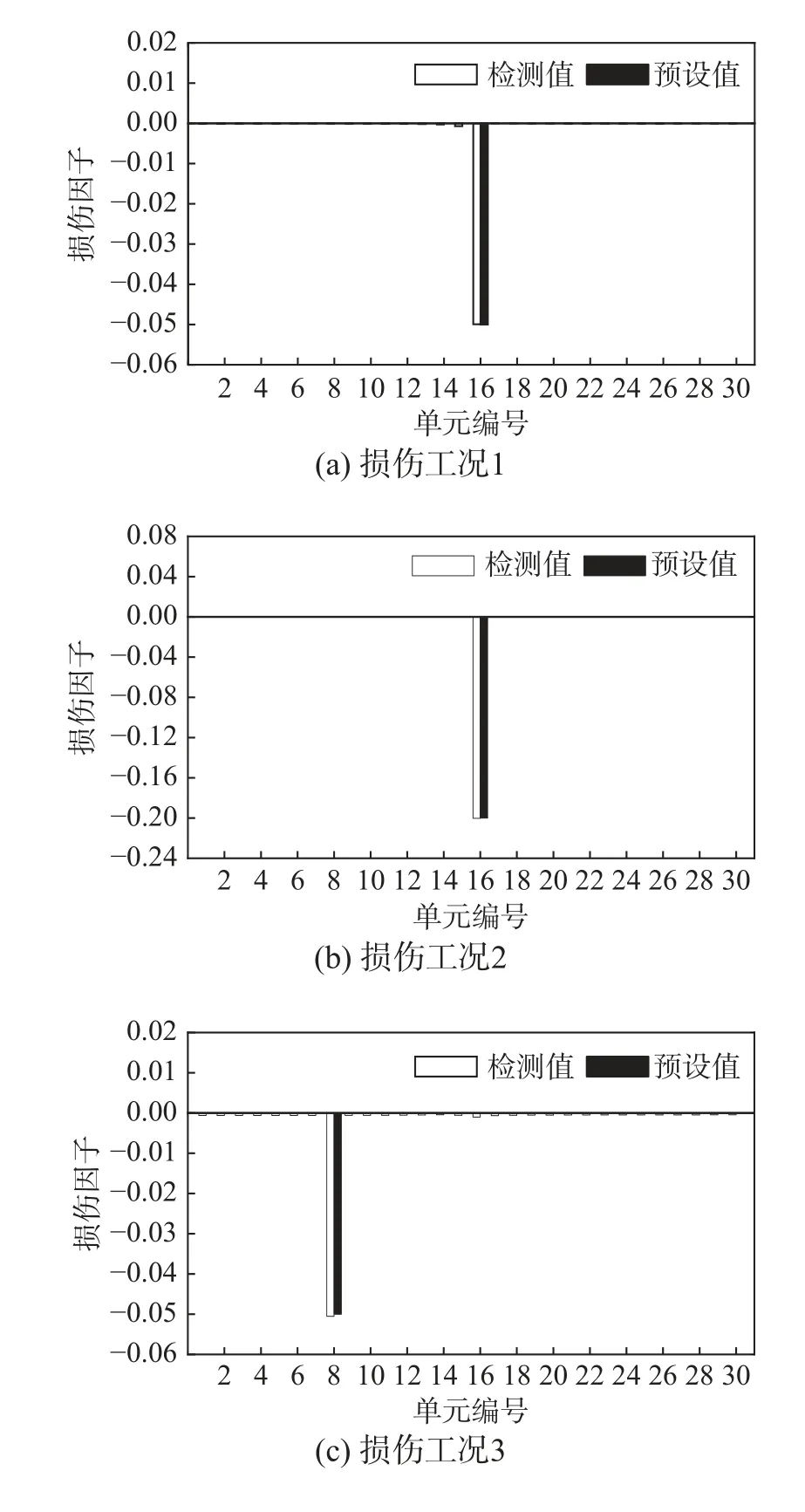
图3 损伤识别结果Fig. 3 Damage identification results

从图3 可以看出，预设损伤的单元的识别结果与实际预设损伤量较吻合度很高，并且未预设损伤的单元上的错误识别很小，可以忽略不计。无论是单个损失还是多个损失的情况，识别结果都令人满意。

2.2 噪声对损伤识别的影响

结构响应信号的测量不可避免地存在噪声，在本研究中，将白噪声添加到每一个单元的应变中，以研究噪声对损伤识别的影响。测量噪声是高斯脉冲过程，其均方根设置为应变最大均方根的百分比。这里使用噪声等级来表征噪声程度，即添加到应变中的噪声是应变最大均方根值等同于噪声等级的高斯过程。结合连续梁数值模拟案例，分析不同噪声等级对损伤识别的影响(噪声等级分别为5%、10%、和15%)。

为了更好地对比说明噪声对该案例中连续梁的损伤识别的影响，对无损伤的连续梁作不同噪声等级下的损伤识别。考虑到高斯白噪声的随机性，在研究噪声对损伤识别的影响时，对损伤工况1、2、5 和6 各设置1000 个对照组，每个对照组随机生成不同的应变测量噪声。由于迭代求解中加入了自适应Tikhonov 正则化方法，各个单元损伤因子的识别值均小于0。用伽马分布拟合全部1000 个对照组识别结果中的各个非预设损伤单元损伤因子识别值，用高斯分布拟合预设损伤单元的损伤因子识别值，分别计算其95%置信区间。损伤工况1、2、5 和6 在不同噪声等级下的各单元识别损伤因子的95%置信区间如图4～图6所示。

图4 5%噪声下的损伤识别结果Fig. 4 Damage identification results under 5% noise

图5 10%噪声下的损伤识别结果Fig. 5 Damage identification results under 10% noise

图6 15%噪声下的损伤识别结果Fig. 6 Damage identification results under 15% noise

从图4～图6 可以看出，在不同的损伤工况中，噪声引起识别结果的波动也不相同，但对于预设损伤值为-0.05 和-0.2 而言，噪声的影响程度差别不大，并不会随着预设损伤的增大而增大；由损伤工况1、5、6 的识别结果可以看出，随着噪声等级的增大，识别结果的波动明显增大，可见噪声对识别存在一定影响。但即使噪声等级提升到15%，识别结果的95%置信区间范围也不超过0.015，对于损伤工况1、5、6 而言是完全可以接受的，识别结果依旧能很好地反映实际损伤情况，而对于损伤工况2 而言，15%噪声的影响可以忽略不计，可见所提出的损伤识别方法对噪声有较好的鲁棒性。

2.3 不同模态对损伤识别的影响

前文对连续梁的损伤识别都依据结构自由振动期间的响应进行，对于该连续梁而言，自由振动表现为单频振动，而有时候土木结构响应可能受到连续加持的外荷载作用(如风荷载、流水荷载等)，此时结构响应通常包含不同的模态成分，且本文所提出的方法是基于结构的模态信息进行损伤识别的，所以要研究不同模态对识别结果的影响。为了使结构响应能包含多个模态成分，将之前施加的冲击荷载改为随机荷载，该随机荷载由6 阶低通巴特沃斯滤波器过滤的均值大于0 的高斯过程模拟，结构响应的各阶模态响应可以反映在结构响应的频谱图上，以16 号单元应变为例，其傅里叶谱如图7 所示。根据图7，这里主要选取有着较明显幅值的前4 阶模态响应来讨论模态阶次的选取对识别的影响。

图7 16 号单元应变数据的傅里叶谱Fig. 7 Fourier spectrum of strain data of Element 16

需要注意的是，对于一些应变模态接近0 的响应，使用EMD 方法提取其模态响应将产生很大的误差，从而无法按照式(5)和式(11)进行近似替代，因此，对于结构中某一阶应变模态为0 或接近0 的位置的损伤情况，无法选取这一阶应变模态用于识别该位置的损伤。在避免出现上述情况的前提下，对表1 中的6 个损伤工况选用不同的模态阶次进行识别以研究选取的模态对损伤识别的影响。对比选用各阶模态的识别结果，多个模态组合如表2 所示。在表2 中，组合1 和组合2 选取的单元模态响应幅值都相对较大，而组合3 中包含了多个幅值较小的模态响应，这里模态响应的幅值可以通过各单元同阶应变模态值的相对大小体现出来。例如，图7 中16 号单元应变的第一、三、四阶模态响应相对于第二阶模态响应而言较小。损伤识别结果如图8 所示。

表2 模态组合Table 2 Damage condition

在图8 中，模态组合1、2 的识别结果区别不大。而模态组合3 包含了多个幅值较小的模态响应，其识别结果较差，因此应尽量选择幅值较大的模态进行损伤识别。此外，相较于图3 中的识别结果而言，在随机荷载作用下的识别误差有所增大，但在本案例中，即使对于预设损伤因子为-0.05 的单元而言，这样的误差依然是可以接受的。

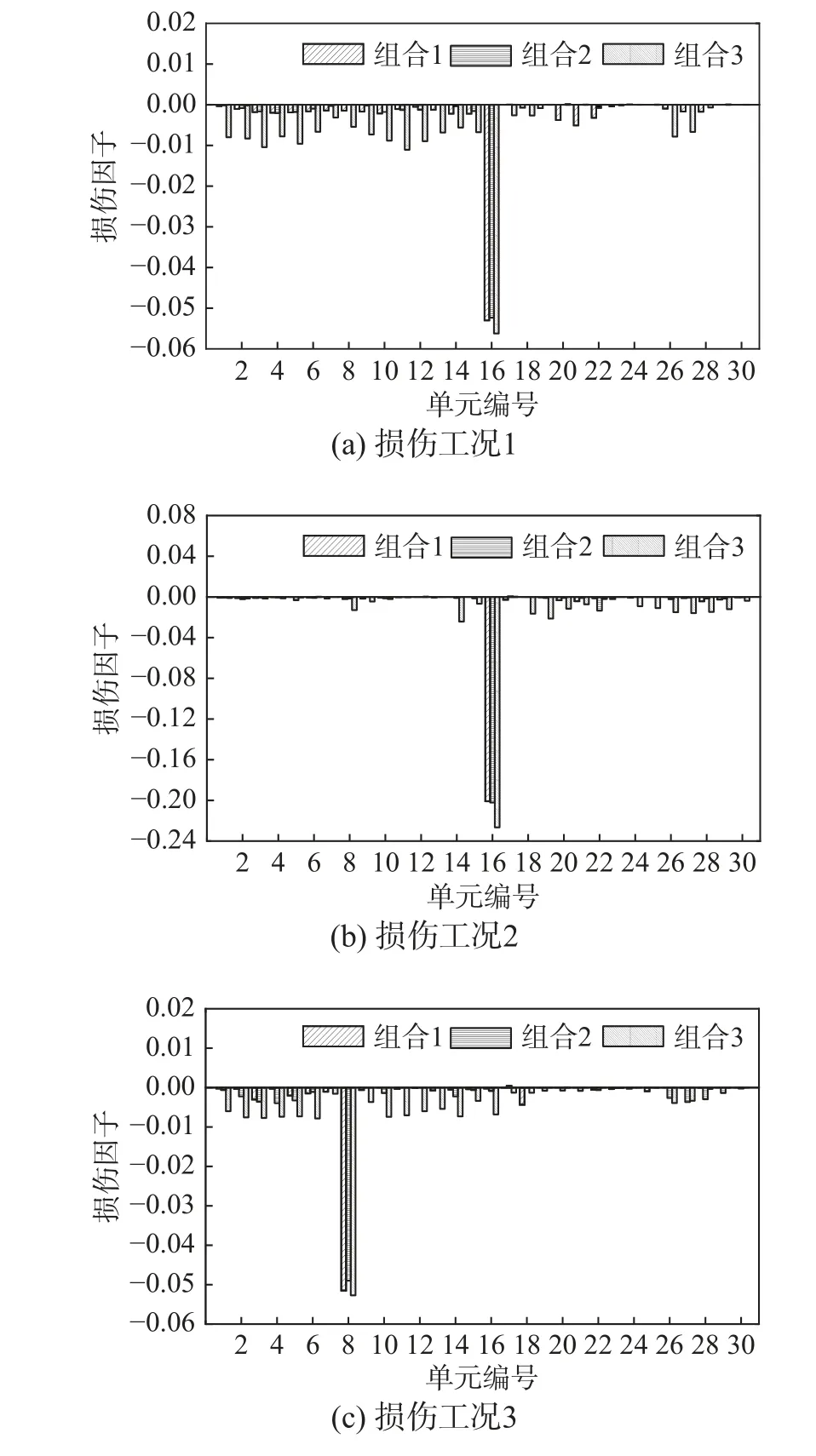
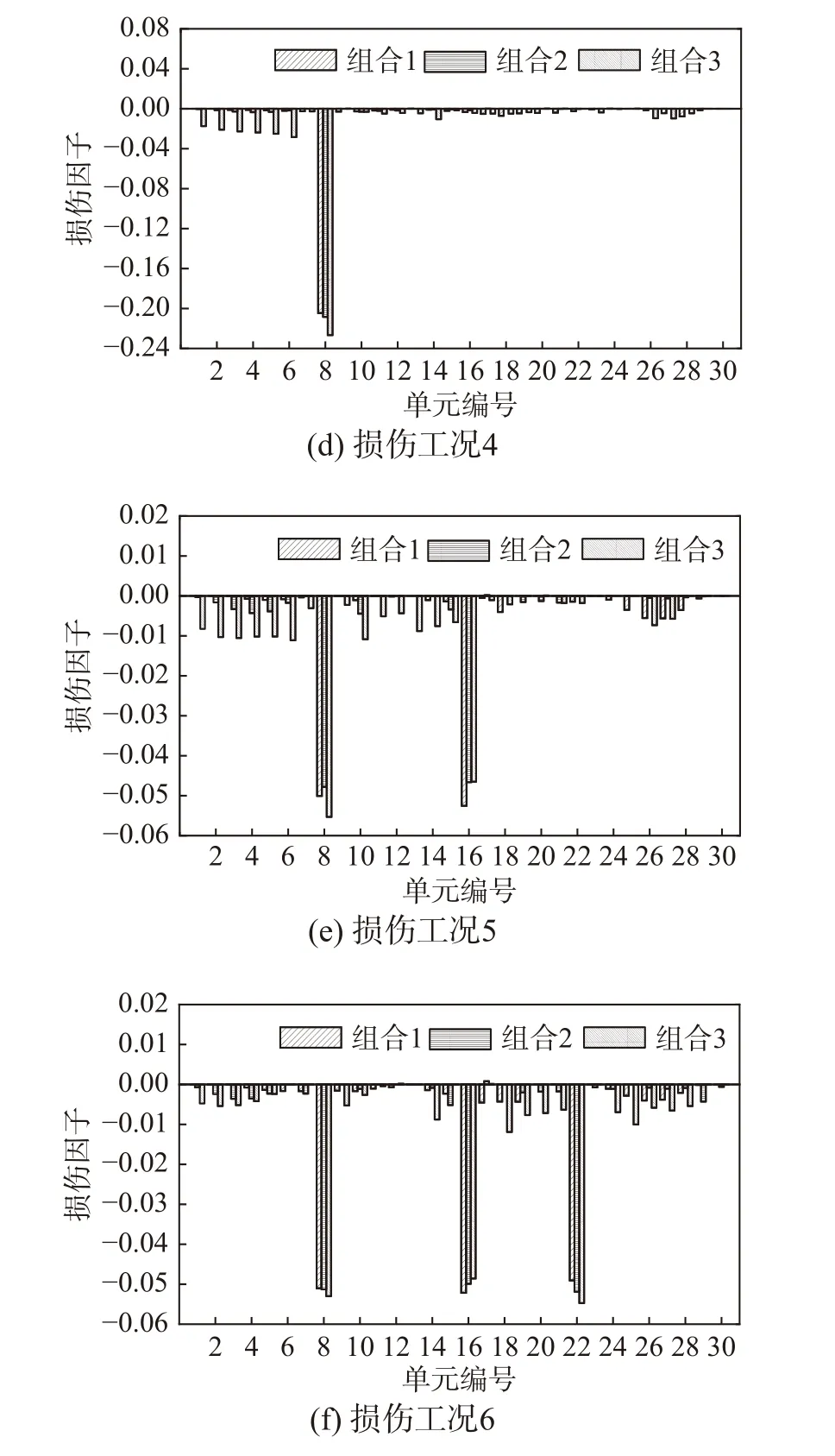
图8 不同模态组合下的损伤识别结果Fig. 8 Damage identification results under different modal combinations

3 结论

本文提出了一种基于应变模态响应重构的损伤识别方法，开展了连续梁单一损伤和多损伤识别仿真计算研究，并探讨了测量噪声和模态阶次选取对识别结果的影响，得主要结论如下：

(1) 该识别方法在时域上实现，不需要进行模态参数识别和时频分析，也不需要获取结构外部激励信息，通过将传感器采集的应变进行经验模态分解分解，得到的模态时域响应信息可直接用于损伤识别，通过连续梁仿真案例验证了该方法的高效性和可行性。

(2) 噪声影响的研究表明，噪声对损伤识别影响很小，对于该案例中的连续梁结构而言，噪声等级达到15%，依然能得到较好的识别结果。在实际工程中，应变测量的噪声等级通常不超过10%，该损伤识别方法在实际运用中对测量噪声具有较强的鲁棒性。

(3) 应变模态接近0 的模态响应无法进行响应重构，从而不能用于损伤识别。除了上述情况外，模态阶次选取影响的研究表明，幅值较大的模态更有利于识别损伤；并且对比使用随机荷载下结构振动响应进行损伤识别，使用自由振动下的结构响应识别能得到更好的结果。

(4) 本文提出的方法，通过对比重构信号与实际信号的差异，通过更新有限元模型获取结构的损伤。在损伤识别过程中，需要在损伤单元布贴有传感器，才能实现对损伤的识别，因此，本方法更适用于对大型结构敏感区域的检测。