嵌入式毂节点刚度及其单层球面网壳承载力研究

张晓磊，李会军，陈 旭，朱志强，喻晓晨

(1. 西北农林科技大学水利与建筑工程学院，陕西，杨凌 712100；2. 陕煤集团神南产业发展有限公司，陕西，榆林 719300)

嵌入式毂节点为一种装配式的半刚性节点，在我国的一些油罐工程、储煤仓库等建筑结构中广泛应用。此类节点既不是理想的刚接节点，也不是理想的铰接节点，而是具有有限刚度的半刚性节点。但该类节点力学性能及其半刚性对网壳稳定性的影响目前仍不完善。因此，有必要针对嵌入式毂节点进行深入的研究，并对此类节点的半刚接网壳的稳定承载力展开深入研究。

国内外学者曾针对常见节点的半刚性特性提出了多种数学模型，如折线性模型、幂函数模型、B 样条模型等[1-3]。Nanda[4]、Hiyama 等[5]对铝合金空间网格结构静力稳定性能作了初步研究，比较了钢结构空间网格结构和铝合金空间网格结构在节点构造方式上的差异，研究表明，节点刚度对铝合金空间网格结构稳定承载能力有明显的影响。廖俊等[6]运用双线性模型拟合了焊接空心球节点的荷载-位移曲线。

范峰等[7]综述了目前各类典型的半刚性节点及相应单层网壳结构的研究成果，并探讨了关于半刚性节点还尚需深入研究的问题。郭小农等[8]拟合了无初始缺陷情况下K6 型铝合金板式节点单层球面网壳的稳定承载力计算公式。朱南海等[9]通过评价结构节点构形度差异性的方法，可以优化结构构件的截面尺寸，从而改善结构整体稳定性。姜守芳等[10]阐述了节点偏差、杆件缺陷与杆件偏心对单层三向柱面网壳的稳定承载能力的影响规律，指出柱面网壳的稳定承载力对节点偏差最为敏感。赵中伟[11]对焊接空心球节点在随机锈蚀后的抗压承载力进行了研究，所提出的概率分布模型理论公式可以预测不同质量损失率所对应的抗压承载力折减系数下限。

王先铁等[12]进行了毂形节点的受力性能试验和有限元数值计算，认为毂形节点的径向受压刚度优于焊接球节点，可在空间网格结构中具备更好的抗压承载力，且该节点在受力性能中拥有很好的延性。李云峰[13]则对榫卯式毂节点的受力性能进行了研究，认为毂型节点在轴压作用下受力性能主要取决于节点接触面的塑性区域。文献[14 - 17]对各类传统节点进行了优化和改进，研究了多种新型节点的受力性能和节点刚度特性。

本文针对常见规格的嵌入式毂节点进行精细化建模，研究了毂节点各部件几何参数对其刚度的影响规律，并拟合获得了节点弯曲刚度的幂函数模型，最后深入探讨了不同结构跨度和矢跨比下节点刚度对网壳稳定承载能力的影响规律，以期为此类节点的单层球面网壳设计提供一定的理论参考。

1 嵌入式毂节点的刚度性能研究

1.1 节点模型

嵌入式毂节点由中心毂体、盖板、中心螺栓、杆端嵌入件、垫圈等部件组成，根据行业标准《单层网壳嵌入式毂节点》(JG/T 136-2016)[18]，利用有限元软件ANSYS 对节点进行建模，整体构件采用实体单元Solid186 进行模拟，本构关系采用理想弹塑性模型，杆件材料为Q235 钢，屈服强度取235 MPa；杆端嵌入件为ZG230-450H 铸钢，屈服强度取230 MPa；毂体部分则采用45 号钢材，屈服强度取355 MPa，弹性模量取206 GPa，泊松比取0.30。建立的节点区域模型如图1 所示，该模型用限制杆件端部节点自由度的方式来实现约束，研究表明该建模分析结果与简化后的节点模型(见图2)计算结果十分接近，本文之后采用简化节点模型进行分析。数值模型的详细几何尺寸参数根据行业标准[18]取值，如表1 所示。

表1 节点的几何尺寸Table 1 Geometric sizes of the hub-shape inlay joint

图1 嵌入式毂节点区域整体模型Fig. 1 Overall region model of the hub-shape inlay joint

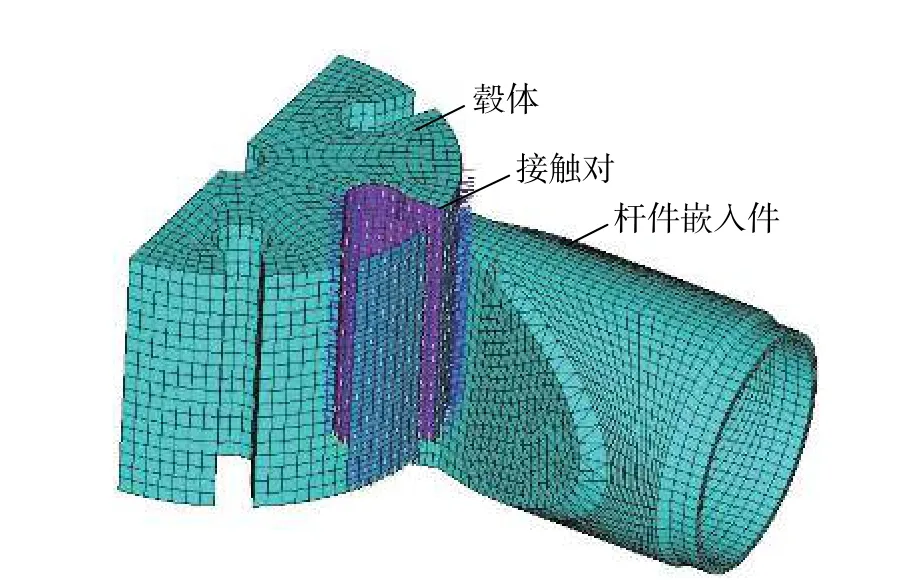
图2 嵌入式毂节点简化计算模型Fig. 2 Simplified calculation model of the hub-shape inlay joint

模型通过Contact174 单元和Target170 单元模拟节点两个接触构件之间的相互作用，计算模型中嵌入榫接触面选用Contact174 表面接触单元，毂体嵌入槽的接触面选用Target170 目标单元。同时，在嵌入榫和毂体侧表面的线接触上也设置了该接触对，嵌入件颈部外端面选用Contact174 单元，毂体侧表面选用Target170 单元，摩擦系数取为0.1。

简化计算模型的上、下表面需施加竖向约束，以此来模拟盖板约束，以防节点出现该方向上的刚体位移。数值模型中杆件倾斜角α 为4°。节点几何尺寸在毂体中的示意图如图3 所示。

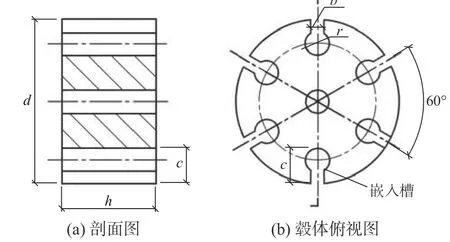
图3 毂体结构示意图Fig. 3 Structural diagram of hub-shape body

1.2 节点轴向刚度和弯曲刚度

在考虑几何非线性和材料非线性情况下，对嵌入式毂节点分别进行受压、受弯及扭转作用的承载力分析，观察节点的破坏过程，可以得到节点在轴心压力作用下的荷载-位移曲线如图4 所示。

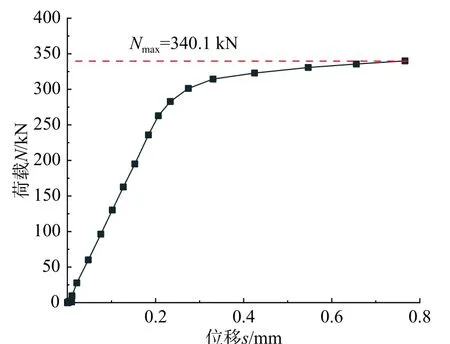
图4 节点在轴心压力作用下的荷载-位移曲线Fig. 4 Load-displacement curve of joint under axial compression

嵌入式毂节点在平面外弯曲作用下、平面内弯曲作用下、扭转作用下的弯矩-转角曲线及扭矩-转角曲线如图5 所示。由图4 和图5 可知，节点在轴心压力作用下的N-s曲线以及平面外弯曲和扭转作用下的M-θ 曲线均具有明显的弹性变形阶段和弹塑性变形阶段，而在面内弯曲作用下，节点在弯矩初加载阶段就呈现出较大的转角，初始刚度K2为11.9 kN·m/rad。当节点受到平面外弯曲作用和平面内弯曲作用时，弯矩作用的中心线均经过杆件嵌入件与毂体嵌入槽侧表面接触的中心处。

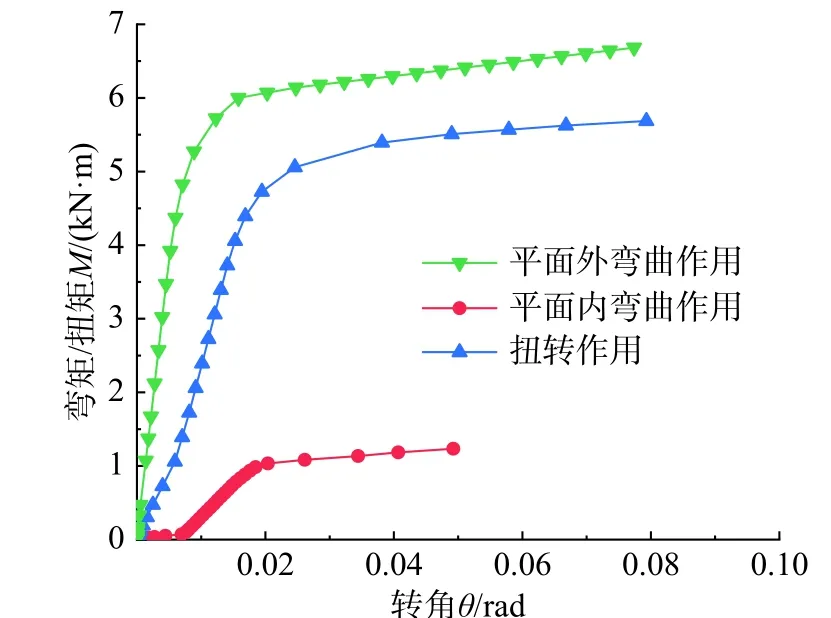
图5 节点的弯矩-转角、扭矩-转角曲线Fig. 5 Moment-rotation and torque-rotation curves of joints

依据行业标准[18]建立多个不同规格的节点数值模型，具体尺寸见表2，上述分析的节点为表中的G114 节点。图6 为G89 节点在面外弯曲作用下的应力云图，图7 为G89 节点在面内弯曲作用下的应力云图。可以看出嵌入件颈部是节点受力时的薄弱部位，该部位需要着重加以考虑。当节点受平面外弯曲作用时，除了毂体整体对杆件嵌入件存在约束作用，还有盖板约束的存在，可以提高杆件的平面外弯曲刚度。而节点在平面内弯曲时，只有毂体嵌入槽可以约束杆件嵌入件的转动，这使得嵌入式毂节点在平面内弯曲时能承受的弯矩作用力较小。

图6 节点在平面外弯曲作用下的应力云图Fig. 6 Stress contour of joint under out-of-plane bending

图7 节点在平面内弯曲作用下的应力云图Fig. 7 Stress contour of joint under in-plane bending

表2 不同嵌入式毂节点的尺寸参数Table 2 Dimension parameters of different joints

1.3 模型结果与试验结果对比

以表2 中的G60、G89 和G133 节点为例，模型在平面外弯曲时的承载力分析计算结果与文献[19]中相同参数节点试验结果的对比如图8 所示，可以看出，该数值模型的计算结果与节点试验结果较为吻合，节点在试验结果的弹性段存在一定的下滑现象，其原因是，试验过程中毂节点的嵌入槽与杆件嵌入榫之间有一定的微小间隙，导致节点在弯矩加载的初始阶段仅能依靠毂体和上下盖板对嵌入榫的摩擦力，该误差属于系统误差。随着荷载不断变大，该间隙消失，有限元模型数据和试验数据也随之接近吻合，验证了本文计算模型的可靠性较强。

图8 模型结果与试验结果对比Fig. 8 Comparison between numerical and experimental results

1.4 幂函数模型

姜栋[19]将毂形节点的面外弯曲刚度分为平滑段、弹性段和塑性段3 个阶段，提出了嵌入式毂节点的三折线模型，但并未研究节点尺寸参数对各阶段节点刚度的影响规律。马越洋[20]运用幂函数模型拟合了齿式节点的弯矩-转角曲线。本文对上述所有规格的节点进行平面外弯曲作用和扭转作用时的承载力分析，基于从工程实用的角度出发，并选取能代表节点弯矩-转角关系曲线特性的各特征参数，将得到的弯矩-转角曲线与Kishi 和Chen[21]所提出的一种幂函数模型进行拟合，以此来较好地表达嵌入式毂节点非线性的弯矩-转角关系，该幂函数模型形式如下：

式中：K为节点的初始刚度；Mu为节点的极限弯矩；n为形状参数。弯矩M和转角θ 的关系可以通过n调节拟合曲线的曲率，该模型示意图如图9所示。可以看出，该模型得出的拟合曲线是一条平滑的曲线，不存在刚度突变的问题，且所需的拟合数据较少、形式直接，是模拟节点半刚性特性的重要模型之一。

图9 幂函数模型示意图Fig. 9 Schematic diagram of power function model

控制节点的单一尺寸参数进行变化，可以得到该尺寸参数作为变量对节点半刚性的影响规律。毂体高度和毂体直径对G89 节点的影响如图10 所示，可知随着毂体高度h和毂体直径d的增大，嵌入式毂节点的初始刚度和极限承载力均会变大。嵌入榫颈部长度c对G114 节点和G89 节点的影响如图11 所示，可以看出节点在平面外弯曲以及扭转时的初始刚度K与节点嵌入榫颈部长度c的关系可以忽略，但在平面外弯曲以及扭转时的极限承载力M需要考虑c的变化。

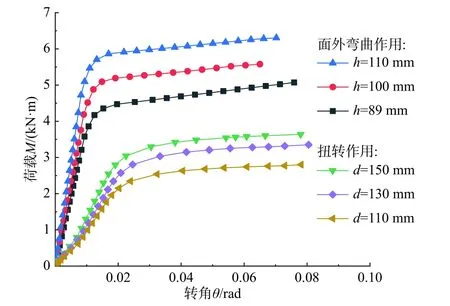
图10 毂体高度h 和毂体直径d 对节点刚度的影响Fig. 10 The influence of hub height h and hub diameter d on the stiffness of the joint

图11 嵌入榫颈部长度c 对节点刚度的影响Fig. 11 The influence of length c of the embedded tenon neck on the stiffness of the joint

运用回归分析法，得出节点在平面外弯曲时的初始刚度K1和扭转时的初始刚度K3与hd的近似关系分别见式(2)、式(3)。

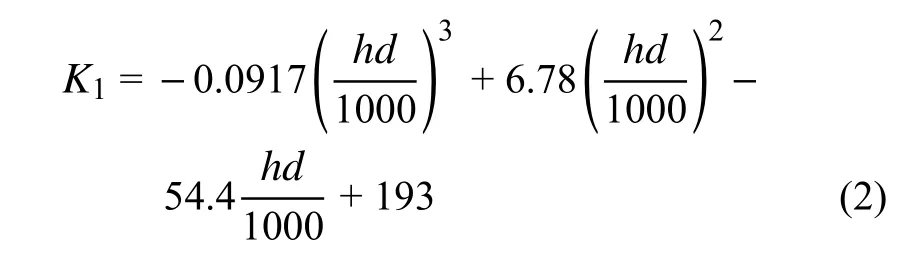
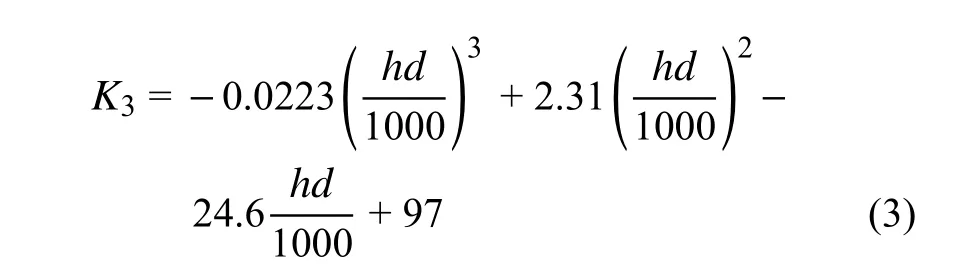
式中：K1、K3的单位为(kN·m)/rad；h为毂体高度，单位为mm；d为毂体直径，单位为mm。

由图11 可知，随着嵌入件颈部长度c的增加，嵌入式毂节点在平面外弯曲作用时的极限承载力有所减小，而扭转作用下的极限承载力会有所增加。参考文献[22]中的空心毂弹塑性承载力公式，同时考虑节点参数变量和加入c的影响因素，得出以下公式：

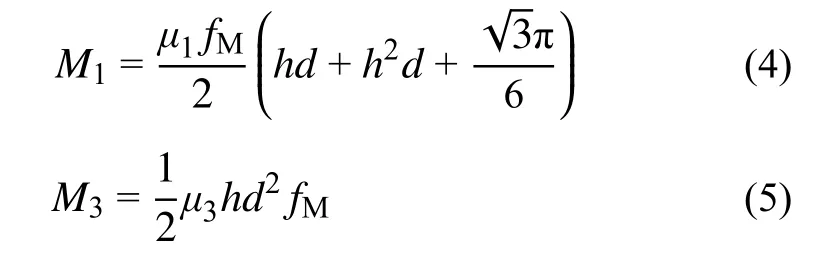
式中：h为毂体高度；d为毂体直径；μ1、μ2为关于嵌入榫颈部长度c的弯矩影响系数和扭矩影响系数；fM为钢材的综合屈服强度标准值，根据嵌入式毂节点的节点刚度对杆端嵌入件和毂体两种钢材屈服强度的相关性，取fM=257.5 MPa。通过回归分析可知，影响系数μ1、μ3与嵌入榫颈部长度c的关系如图12 所示，即可得μ1、μ3与c的关系如下：

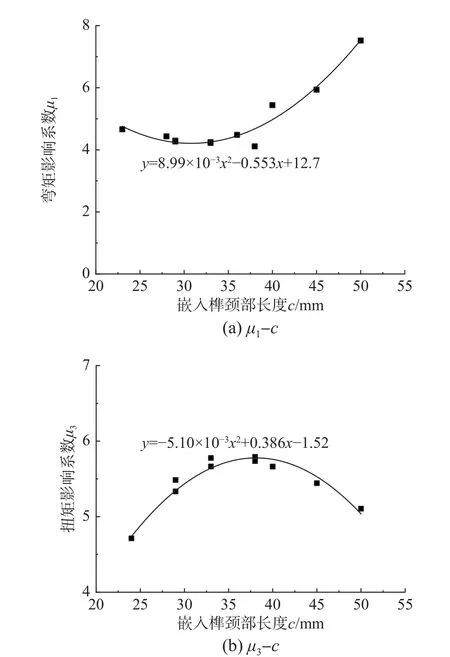
图12 μ1、μ3 与c 的关系图Fig. 12 The relation among μ1、μ3 and c

最后确定模型中形状参数n的取值，表2 中各节点在平面外弯曲作用下弯矩-转角曲线幂函数模型的形状参数n1的取值如表3 所示，在扭转作用下扭矩-转角曲线幂函数模型的形状参数n3的取值如表4 所示。

表3 节点在平面外弯曲作用下幂函数模型中的形状参数Table 3 Shape parameters in power function model of nodes under out of plane bending

表4 节点在扭转作用下幂函数模型中的形状参数Table 4 Shape parameters in power function model of joints under torsion

为确定形状参数n与嵌入式毂节点各尺寸参数的关系，需要先确定一个无量纲量hd/c2，形状参数n与该无量纲量的关系如图13 所示。

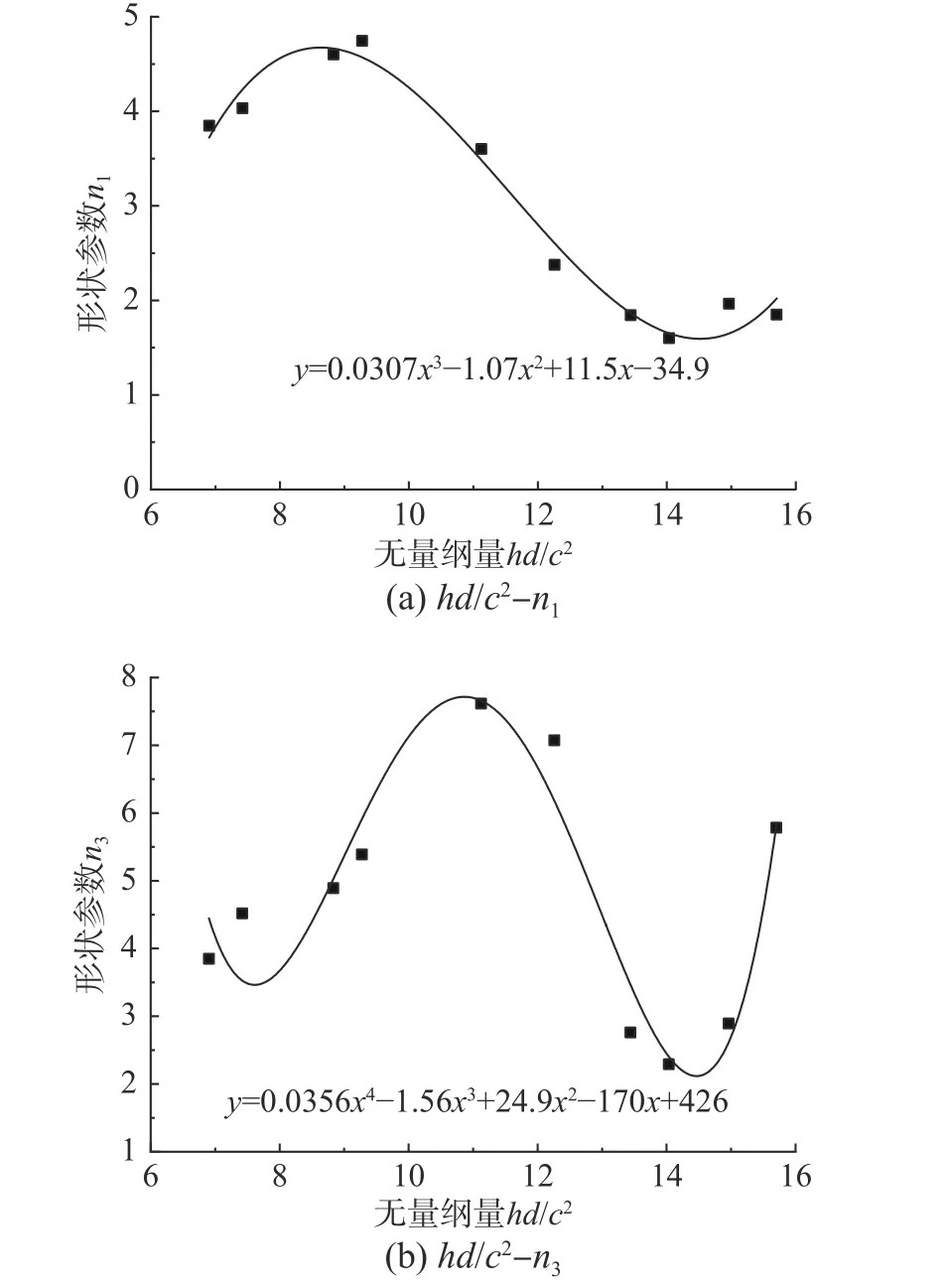
图13 hd/c2 与n 的关系图Fig. 13 The relationship between hd/c2 and n

由图13 可知，节点在平面外弯曲作用下形状参数n1的表达式和在扭转作用下形状参数n3的表达式如下：

综上所述，嵌入式毂节点在面外弯曲作用下，初始刚度K1由式(2)计算，极限承载力M1由式(4)计算，形状参数n1由式(8)计算；在扭转作用下，初始刚度K3由式(3)计算，极限承载力M3由式(5)计算，形状参数n3由式(9)计算。节点刚度实际M-θ 曲线与通过上述公式计算的节点刚度幂函数模型曲线的对比图如图14 所示。

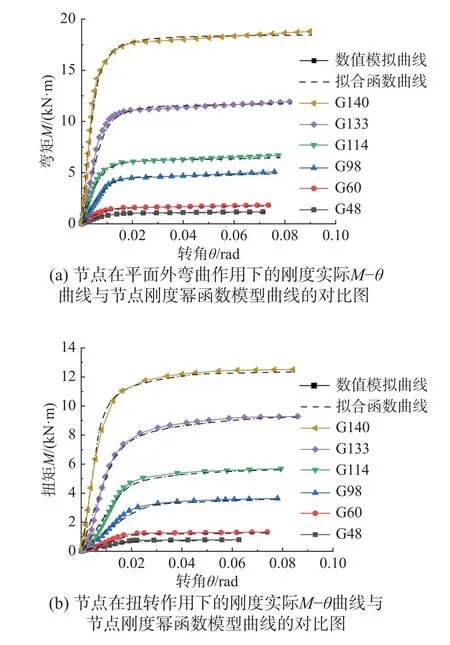
图14 节点刚度实际M-θ 曲线与节点刚度幂函数模型曲线的对比图Fig. 14 Comparison diagram between actual M-θ curve of joint stiffness and power function model curve of joint stiffness

由图14 可以看出，嵌入式毂节点的刚度幂函数模型与数值分析结果吻合良好，可为此类节点在实际工程中的设计计算提供参考。

2 半刚接单层球面网壳的稳定性研究

2.1 网壳模型

本文以K8 型单层球面网壳为例来分析嵌入式毂节点对整体结构的影响，其结构形式如图15 所示，网壳跨度40 m、曲率半径42.5 m、矢跨比为1/8[23]。结构杆件均采用圆钢管，主肋及环向杆截面尺寸为114 mm×5 mm，斜杆截面尺寸为108 mm×3.5 mm。根据规范，毂体高度应按照节点区域内截面高度最大的杆件来选取，对于较小截面高度的杆端，毂体嵌入槽上、下应采用圆形垫块进行垫平，即网壳节点处均采用G114 节点。杆件材料为Q235 钢，弹性模量为2.06×105MPa、泊松比为0.3、密度为7.85 g/cm3，模型采用等向强化Mises 理想弹塑性材料，结构周边节点为三向固定铰支座。

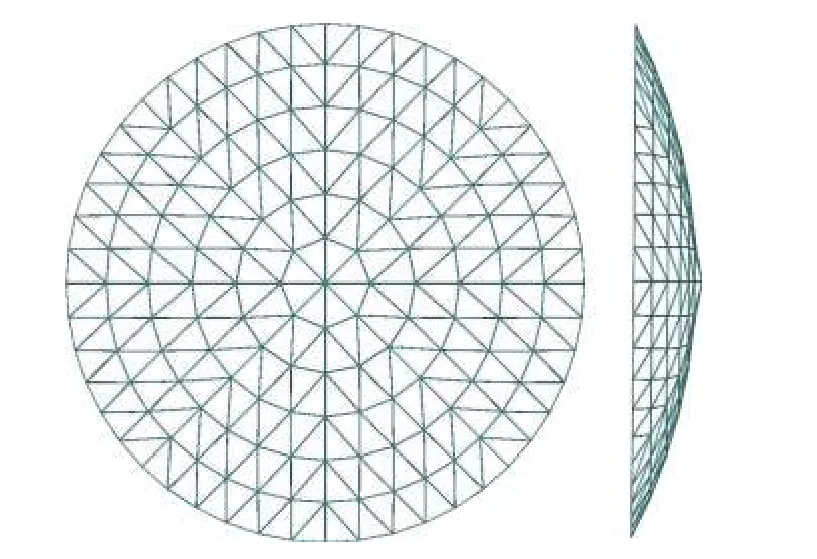
图15 K8 单层球面网壳结构Fig. 15 K8 single-layer spherical reticulated shell

节点域的节点刚度力学模型示意图如图16 所示，杆件在相交处建立刚性节点域，运用非线性弹簧单元Combin39 将G114 节点的刚度数据输入到杆件端部的各个方向的自由度上，根据前述内容中G114 节点刚度模型的分析数据，将节点刚度输入到半刚接网壳中，其中节点在平面外弯曲方向上的抗弯刚度为Kbz，在平面内弯曲方向上的抗弯刚度为Kby，节点轴向抗压刚度为Kax。

图16 节点刚度物理意义示意图Fig. 16 Schematic diagram of physical meaning of joint stiffness

本文设计了用于对照的刚接网壳，采用Combin14单元来表达杆件端部6 个方向的自由度，设Kax=Ksy=Ksz=1015N/m，Kby=Kbz=Ktx=1015(N·m)/rad，以此来模拟节点处的刚接特性。

2.2 不同类型的节点刚度对网壳承载能力的影响

将不同的节点刚度特性带入到网壳结构中进行分析，可以研究节点刚度对网壳极限承载力的影响程度。通过非线性分析，可得出在不同类型的节点刚度下网壳结构的极限承载力，如图17 所示，其中节点在各方向上均为刚接的理想刚接网

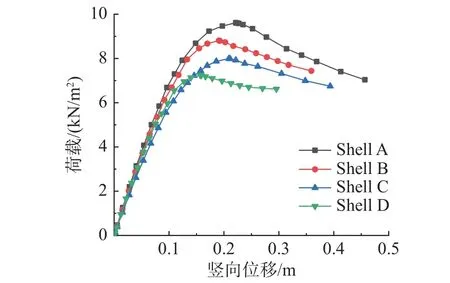
图17 不同节点刚度下网壳结构的荷载-位移曲线图Fig. 17 Load displacement curves of reticulated shells with different joint stiffness

壳为Shell A；节点只具备有限的轴向刚度Kax，而在其他方向上刚接的半刚接网壳为Shell B；节点具备有限的弯曲刚度Kbz、Kby，而在其他方向上刚接的半刚接网壳为Shell C；节点同时具有轴向刚度Kax、弯曲刚度Kbz和Kby，而在其他方向上刚接的半刚接网壳为Shell D。图中的纵坐标为网壳结构单位面积上的均布荷载值，横坐标为网壳结构中最大竖向位移点的位移量。

表5 给出了各类网壳的极限承载力以及荷载折减系数KN，荷载折减系数KN为半刚接网壳极限承载力与相对应的理想刚接网壳极限承载力的比值。可以看出，节点刚度的存在会使得网壳的极限承载力呈现下降趋势，也使得初始阶段的整体刚度有所下降，结构的极限承载力和极限承载临界状态下的节点最大位移值均会因节点刚度的存在而减小，且对节点弯曲刚度的敏感程度大于节点轴向刚度，两种节点刚度同时作用下会使得网壳的极限承载力进一步下降。网壳结构在最大承载力临界状态之后存在下降段，下降幅度会因节点刚度的存在而出现减缓的趋势。

表5 不同节点刚度下网壳的极限承载力Table 5 Ultimate bearing capacity of reticulated shells with different joint stiffness

图18 给出了网壳Shell A～Shell D 在极限承载力作用下的节点位移。可以发现，除了只输入有限弯曲刚度的半刚接网壳(Shell C)的最大位移的节点位于第五肋环与主肋的交点上，其他三种形式的网壳结构最大位移节点均位于第一肋环上，这表明节点弯曲刚度对网壳承载力的影响不能忽略。

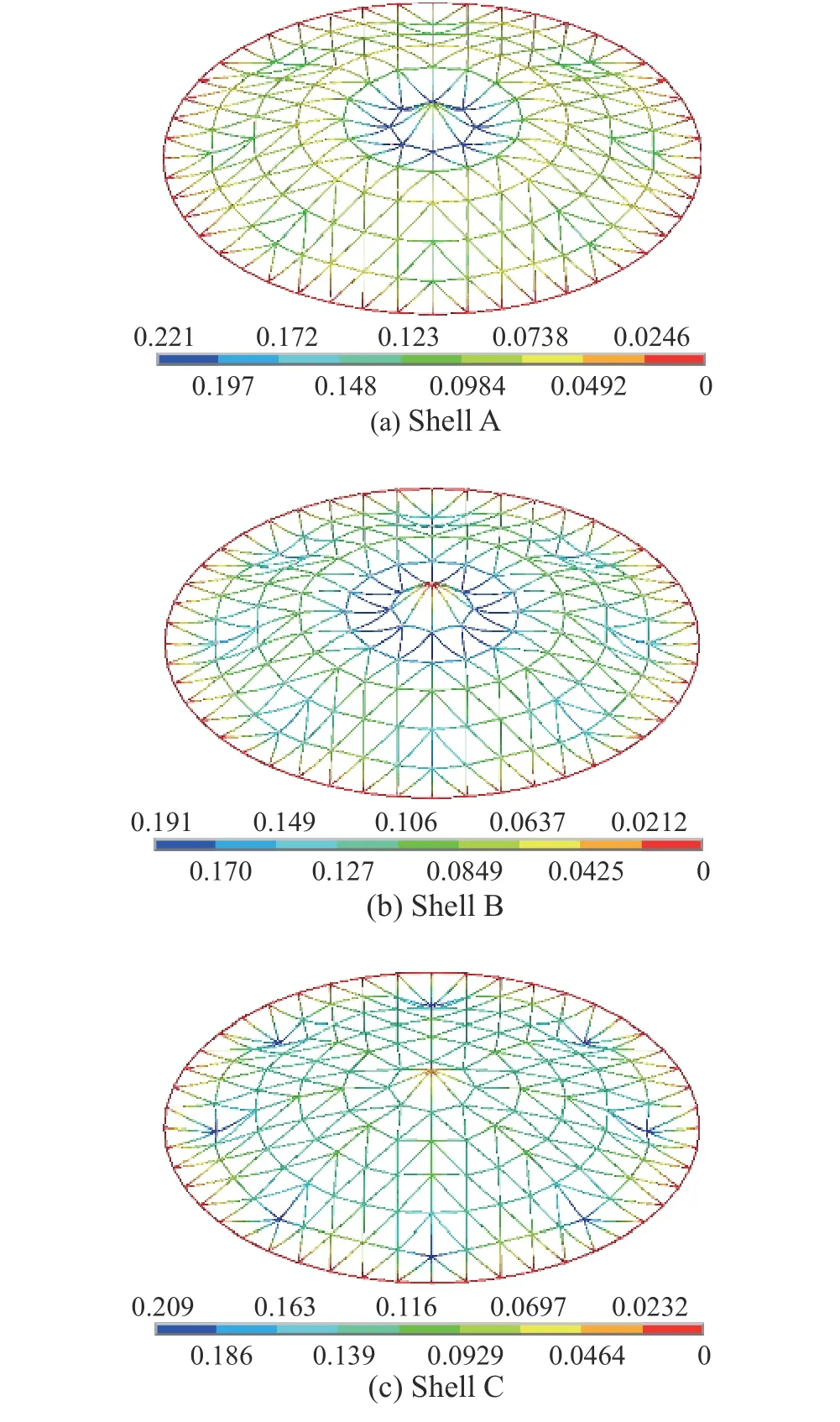
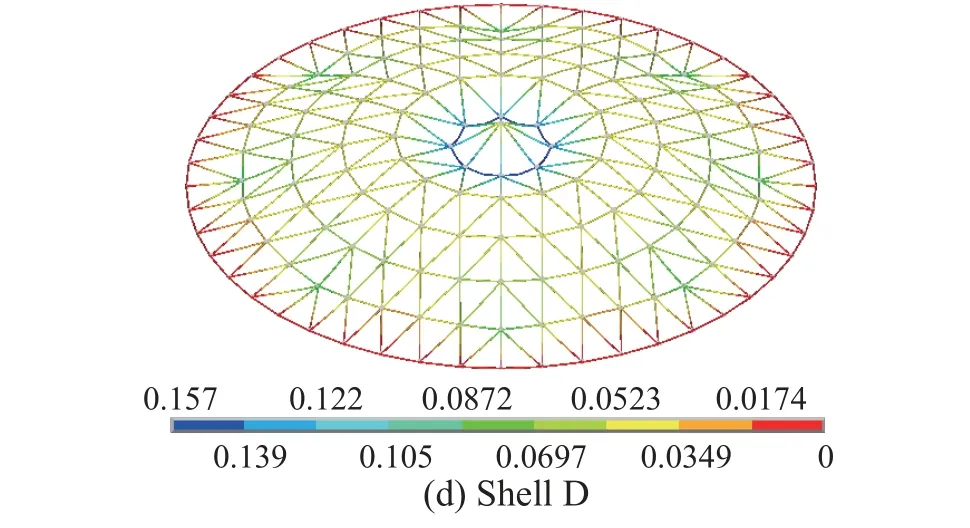
图18 网壳Shell A～Shell D 在极限承载力临界点时的节点位移图Fig. 18 Joint displacement diagram of Shell A～Shell D at critical point of ultimate bearing capacity

2.3 跨度和矢跨比对半刚接网壳承载力的影响

保持上述同时具有轴向刚度Kax和弯曲刚度Kbz、Kby的半刚接网壳其他参数不变，改变网壳跨度和矢高来探究半刚接网壳极限承载力的变化规律，选用了跨度L为30 m、40 m、50 m，矢跨比分别为1/4、1/5、1/6、1/7 和1/8 的网壳进行对比分析。图19 给出了网壳中最大竖向位移节点的荷载-位移曲线，结果表明，网壳整体结构的初始刚度会随着结构矢跨比的减小而减小。图20 则给出了不同跨度和矢跨比的半刚接网壳在极限承载力临界时刻下的节点位移图，观察网壳的失效模式可以发现半刚接网壳的薄弱部位依然在网壳顶部；半刚接网壳的倒数第二圈肋环与主肋的相交处会随着矢跨比的减小而逐渐产生较大的位移。

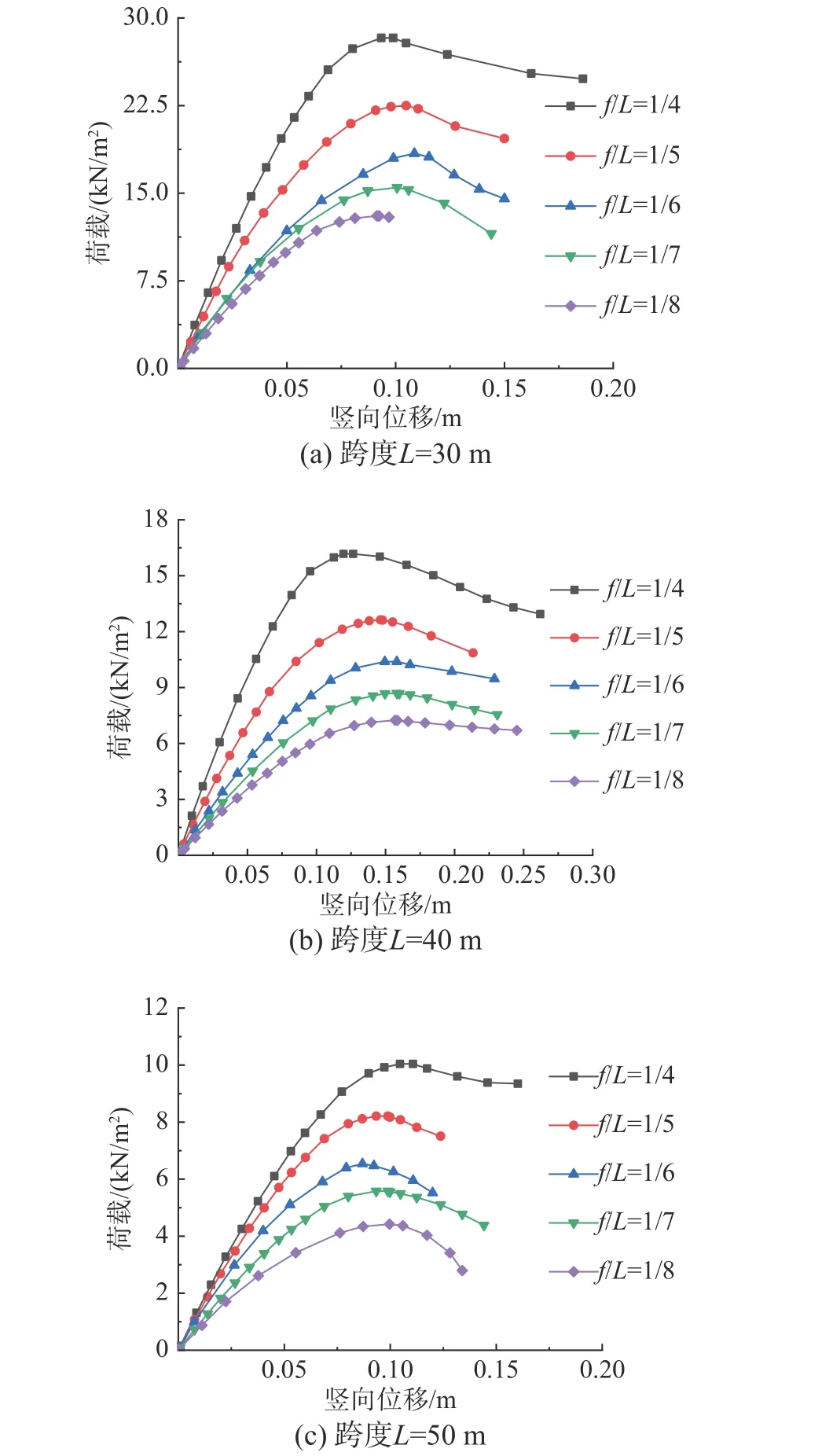
图19 不同矢跨比和跨度下半刚接网壳的荷载-位移曲线Fig. 19 Load displacement curves of semi-rigid reticulated shells with different rise span ratios and spans

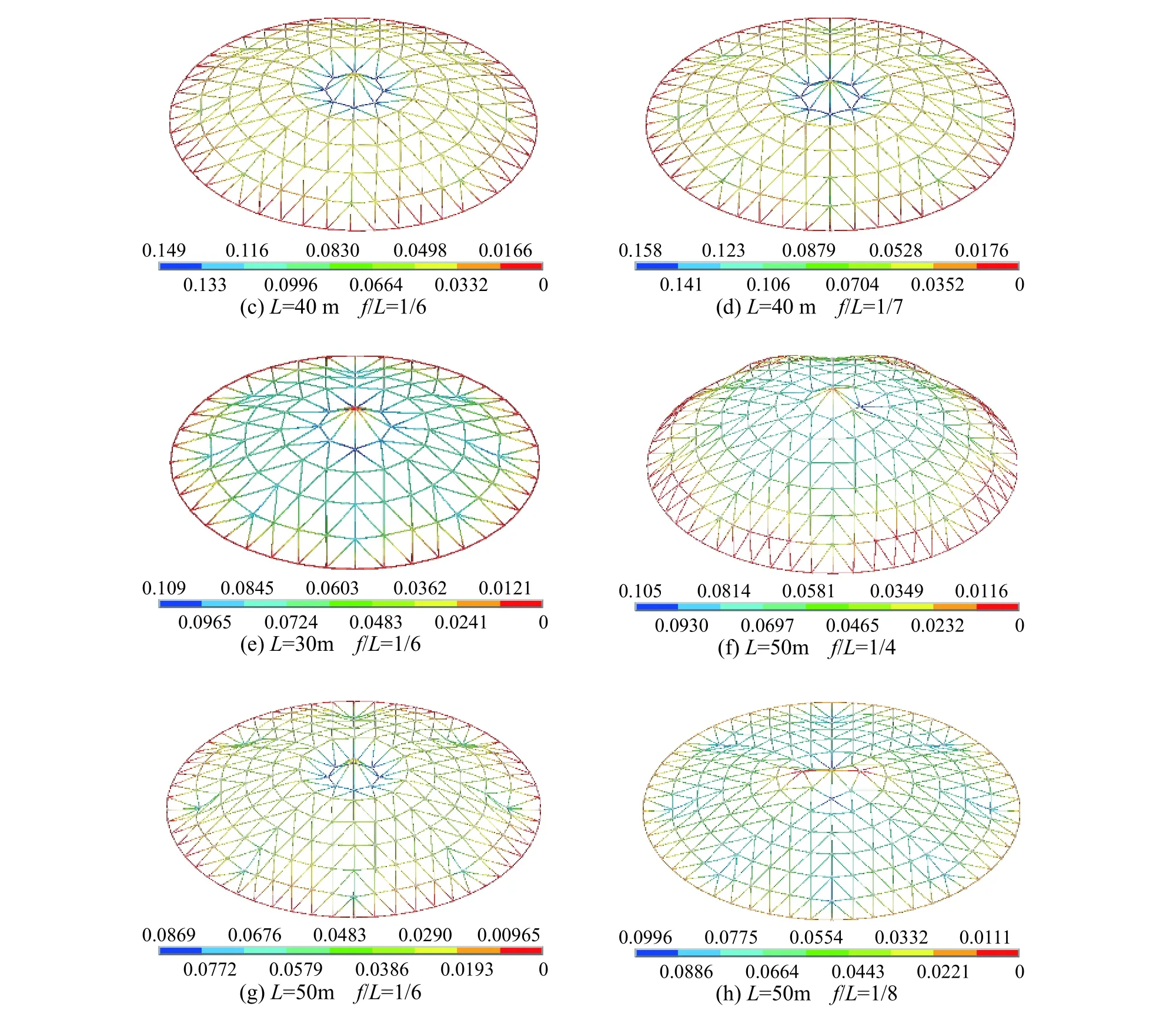
图20 不同跨度和矢跨比下半刚接网壳在临界时刻的变形图Fig. 20 Deformation diagram of semi-rigid reticulated shells at critical state under different spans and rise-to-span ratios

对于跨度在50 m 的半刚接网壳，网壳顶部由于较大的跨度使得结构在不同矢跨比下的破坏形状并不类似。与矢跨比为1/6 时相比，矢跨比为1/4 时网壳顶部第一肋环处向下位移的节点数减少，且主肋的变形并不明显，变形区域更向网壳顶部集中。当矢跨比为1/8 时顶部第一肋环处会产生与网壳顶点相当位移量的两个节点。

不同跨度和矢跨比下网壳的极限承载力和荷载折减系数KN如表6 所示，可以看出网壳在不同跨度和矢跨比下的荷载折减系数KN均在0.75 以上，这表明，嵌入式毂节点可以运用到K8 单层球面网壳的节点设计当中。

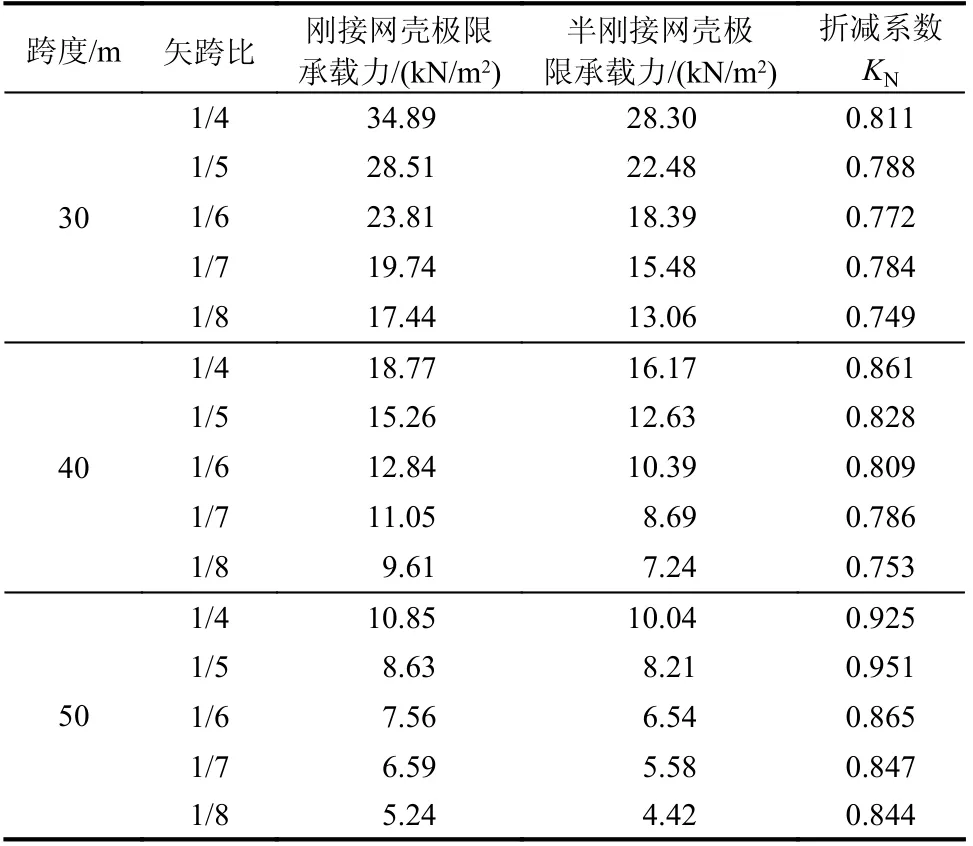
表6 矢跨比和跨度对半刚性网壳极限承载力的影响Table 6 Influence of rise span ratio and span on ultimate bearing capacity of semi rigid reticulated shells

图21 给出了不同跨度下刚接网壳以及同时具有节点弯曲刚度和轴向刚度的半刚接网壳的极限承载力受矢跨比变化的影响规律。结果表明，对于相同矢跨比的K8 单层球面网壳，极限承载力对节点刚度的敏感程度会随着跨度的增大而降低，当结构跨度达到50 m 时，刚接网壳和半刚接网壳的极限承载力已较为接近，荷载折减系数KN均在0.84 以上。此外，即便网壳跨度在不断增加，矢跨比从1/4 下降到1/8 的过程中，三种不同跨度的半刚接网壳的承载能力平均下降幅度为54.99%，没有太大差异。

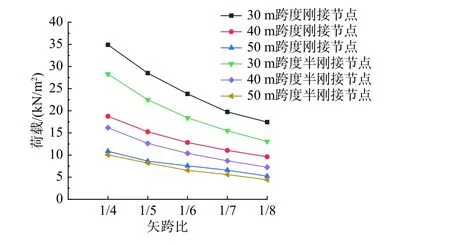
图21 刚接和半刚接网壳在不同矢跨比和跨度下的极限承载力Fig. 21 Ultimate bearing capacity of rigid and semi-rigid reticulated shells with different rise-span ratios and spans

半刚接网壳的荷载折减系数KN随矢跨比和跨度的变化曲线如图22 所示。可以看出，在跨度相同的情况下，半刚接网壳的荷载折减系数KN随矢跨比的减小基本呈下降的趋势，即矢跨比越小，半刚接网壳的承载能力越容易受到节点刚度的影响。在矢跨比相同的情况下，半刚接网壳的荷载折减系数KN随跨度的增加基本上呈上升的趋势，即跨度越小，半刚接网壳的承载能力越容易受到节点刚度的影响。

图22 不同跨度和矢跨比下半刚接网壳的荷载折减系数KNFig. 22 Load reduction factors KN of semi-rigid reticulated shells with different spans and rise-to-span ratios

3 结论

本文对常用规格下的嵌入式毂节点进行了精细化建模，通过参数化分析，建立了与毂体高度、毂体直径及嵌入榫颈部长度相关的弯矩-转角曲线和扭矩-转角曲线幂函数模型。在此基础上，建立了其半刚接单层球面网壳模型，研究了不同跨度、矢跨比下节点刚度对网壳稳定承载能力的影响，并将其与理想刚接网壳进行了稳定承载能力对比，主要得出如下结论：

(1) 该嵌入式毂节点模型的数值计算结果与试验结果吻合良好，且节点在面外弯曲作用和扭转作用下的M-θ 曲线可以运用幂函数模型进行拟合，通过回归分析法能够确定模型中初始刚度、极限承载力以及形状参数与节点主要尺寸之间的关系。该幂函数模型与节点的数值计算结果较为吻合，可为此类节点的设计和应用提供参考。

(2) 与刚接网壳相比，半刚性的毂节点会使得网壳的极限承载力下降，且节点弯曲刚度对承载力的影响程度大于节点轴向刚度，在两者共同的作用下网壳极限承载力会进一步下降，节点弯曲刚度对网壳承载力的影响不能忽略。

(3) 采用嵌入式毂节点的K8 单层球面网壳的极限承载力与相应的理想刚接网壳相比，折减系数KN均在0.74 以上，表明嵌入式毂节点可以应用于K8 单层球面网壳结构。

(4) 半刚接网壳的承载能力对节点刚度的敏感程度会随着网壳矢跨比的减小而增大，也会随着结构跨度的减小而增大。当结构跨度达到50 m 时，刚接网壳和半刚接网壳的极限承载力已较为接近，荷载折减系数KN均在0.84 以上。