城市道路下混合动力汽车双层能量管理策略
唐香蕉 高祖成 曾令全 赵奕凡
上汽通用五菱汽车股份有限公司,柳州,545000
0 引言
网联自动驾驶汽车(connected and automated vehicle, CAV)可通过车辆与基础设施(vehicle-to-infrastructure, V2I)及车辆与车辆(vehicle-to-vehicle, V2V)的无线通信技术,获取、交换和共享车辆本身及周围交通流的状态信息[1],在此基础上研究面向动态交通流的智能化能量管理策略(energy management system, EMS),从而显著改善车辆机动性、安全性和燃油经济性等多维性能[2],已成为未来智能交通系统(intelligent transportation system, ITS)最具潜力的应用之一。
面向ITS场景的“生态驾驶”是CAV节能技术的集中体现,它是指根据当前及未来交通流约束,以提升整车燃油经济性为目标,规划车辆车速轨迹[3]。如MANDAVA等[4]、ASADI 等[5]通过V2I通信获取交通信号灯未来时序,分别运用动态规划(dynamic programming, DP)和模型预测控制算法,以穿过多个路口时最大化遇到绿灯信号概率和保持较低的燃油消耗为综合目标,获得了最优驾驶车速轨迹。SUN等[6]同样采用DP算法,提出了一种高鲁棒性的生态驾驶策略以减小不确定性场景下交叉口的停车概率,与改进的智能驾驶员模型相比,该方法可将车辆燃料消耗减少10%以上。AMINI等[7]基于预测的交通流信息,对混合动力CAV的速度及功率分配进行了时域滚动优化,节能率可达8.8%。此外,粒子群优化[8]、等效燃油消耗最小化策略[9]和强化学习[10]等方法也经常被用于生态驾驶问题求解中,均取得了较为理想的效果。
上述优化方法应用在短距离路口场景时具有较为理想的节能表现,但是在城市道路实际场景中,系统需要规划多个连续十字路口,这对算法的实时性能提出了更高的要求。例如,OZATAY等[11]考虑交通流在各个交叉口的到达时间,构建了两阶段求解方法,简化了问题的计算复杂程度,获得了多交叉口燃油消耗最低的最优速度轨迹。BUTAKOV等[12]考虑交通信号灯位置和通信延迟约束,通过强制车辆通过每个绿灯的时间区间以减少算法“遍历”求解时的时间,进而快速优化得到最优行驶速度。
多路口信号灯时序重叠下的生态驾驶路径规划是典型的高维非线性规划(non-linear programming, NLP)问题,传统方法难以利用有限计算资源快速获得全局最优速度规划,而伪谱法(pseudo-spectral method, PM)作为求解NLP问题的典型直接方法,已经越来越多地应用于求解各种动态系统的最优控制数值解[13]。本文面向联网应用场景,提出了一种基于伪谱法的分层优化求解方法,采用双层求解架构,快速实现多路口城市道路下混合动力车辆(hybrid electric vehicle, HEV)的速度规划和能量管理优化,充分发挥联网通信在车辆节能方面的巨大潜力。
1 混合动力车辆及交通信号灯时序建模
1.1 混合动力车辆模型
图1所示为所研究的串联式混合动力汽车结构。经过单级减速的牵引电机为车轮提供驱动力。发动机-发电机组(engine generator set, EGS)和电池组由电源分配单元(power distribution unit, PDU)控制,共同向电机供电。通过优化EGS和电池组之间的功率分配,可提高整车燃油经济性。
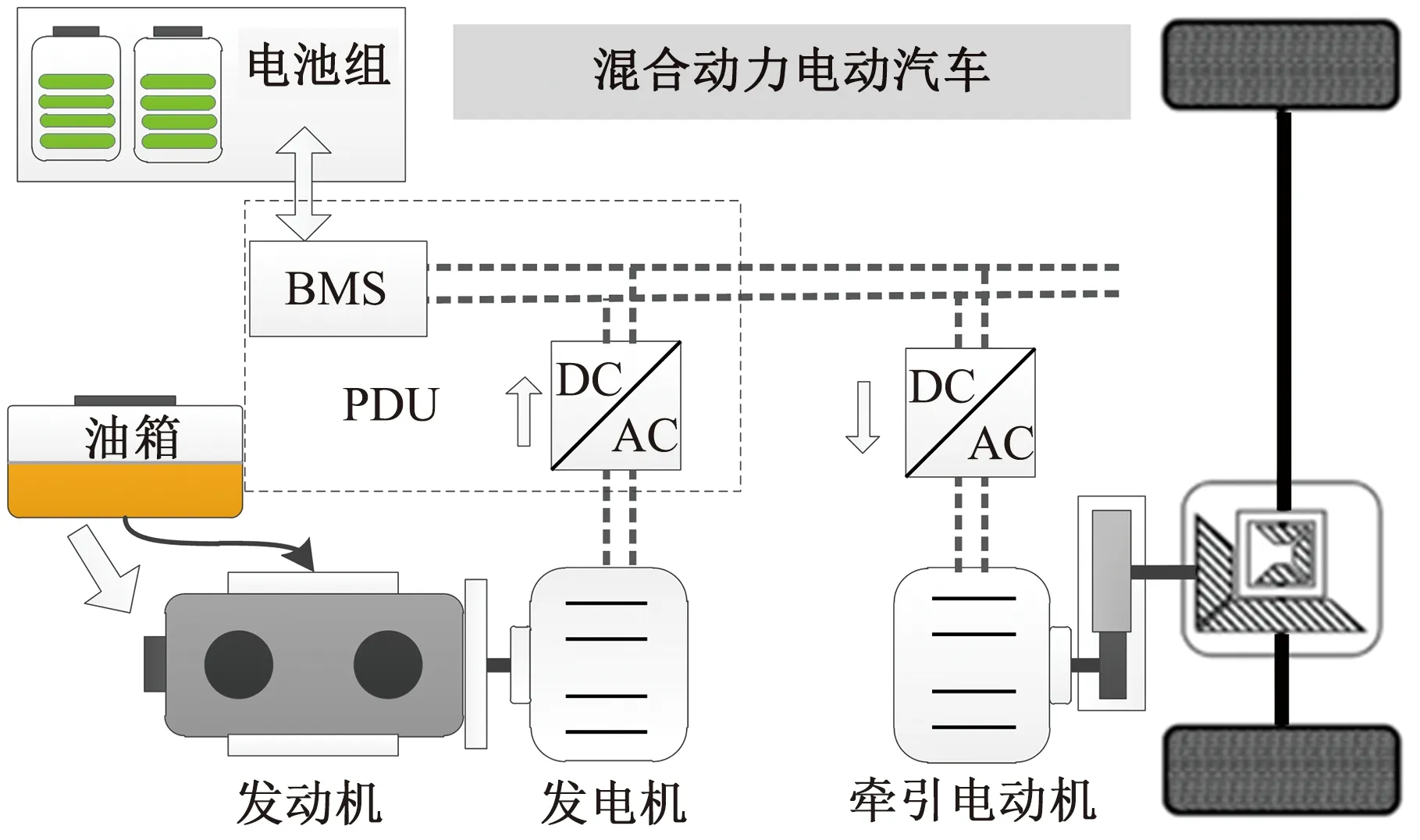
图1 串联式混合动力汽车结构Fig.1 Structure of series hybrid electric vehicle
忽略车辆的轮胎滑动,构建车辆的一维运动方程如下:
(1)
式中,v为汽车车速;Ftrac为车辆牵引力;M为车辆等效质量;fr为滚动阻力系数;ρ为空气密度;Af为迎风面积;Cd为空气阻力系数;α为路面坡度。
定义s(t)为车辆的行驶距离、e(t) 为车辆行驶过程中的总能量消耗,车辆状态向量表示为X(t)=(s(t),v(t),e(t))T。则车辆在t时刻的非线性纵向运动一般可以用状态更新方程来表示:

(2)
其中,u(t)表示控制量。系统暂时不考虑车辆的制动能量回收,使用线性公式拟合车辆的行驶能耗,根据文献[14]得到匀速巡航时的能耗功率公式Pcruise=b3v3+b2v2+b1v+b0,牵引力加速行驶时的能耗功率表示为Ptrac=(a2u2+a1u+a0)uv,其中,u表示车辆加速度。因此,驱动电机的电能消耗功率Pm可以表示为
Pm=(a2u2+a1u+a0)uv+
(b3v3+b2v2+b1v+b0)
(3)
其中,a2、a1、a0、b3、b2、b1、b0均为固定系数。通过实车数据拟合标定获取式(3)中各项系数时,借鉴文献[15]的数据采集方法,通过测量车辆在不同车速时给出的不同制动量所产生的制动减速度,构建制动量-减速度-速度关系。通过测量车辆在不同加速踏板行程下的电机转矩-转速关系曲线构建油门控制量-转矩-速度关系。在测量的同时统计电池母线电压、电流计算电能消耗。最后用数据拟合分别得到匀速与变加速过程中的消耗曲线。
若不考虑车辆附件的损耗,根据能量守恒,存在以下等式关系:
(4)
式中,ηm为电机的效率,由电机的转速和转矩共同决定;ηb为电池的效率。
EGS和动力电池是该混动系统的核心部件,下面分别介绍这两大部件的数学模型。
1.1.1EGS模型
发电机的输出电压和转矩可以表示为
(5)
式中,Ug、Ig分别为发电机的电压和电流;Ke、Kx分别为电动势系数和电阻系数;Tg、Wg分别为发电机的转矩和转速。
发动机和发电机的动力学耦合关系如下:
(6)
式中,Te为发动机扭矩;ne为发动机转速;ie-g为发动机-发电机组的减速比;ηe-g为发动机到发电机的平均效率;Je、Jg分别为发动机和发电机的转动惯量;γ为发动机节气门开度。
发动机的最大转矩和油耗随转速的变化关系如图2所示。

图2 发动机最大转矩和油耗曲线Fig.2 Engine maximum torque and fuel consumption curve
1.1.2电池模型
采用常见的电压源串联欧姆内阻模型对电池进行建模,如图3所示。电池的端电压Ubat可以表示为
Ubat,t=Uocv,t+Ri,tIbat,t
(7)
其中,t表示时刻序号;Uocv,t表示电池的开路电压。电池的激励电流Ibat在放电时为负值,在充电时为正值。Ri表示电池内阻。电池荷电状态SOC值可通过下式进行更新:
(8)
式中,Δt为相邻时刻间的间隔;η为电池的充放电效率;Cbat为电池的容量。

图3 电池的等效电路模型Fig.3 Equivalent circuit model of battery
1.1.3功率分配与模型验证
由于本文研究的混合动力系统为串联式结构,动力总成的功率分配还须满足以下方程:
(9)
其中,Udc为母线电压,Pe为EGS的功率输出,Pb为电池的功率输出。根据实车试验数据对动力系统模型进行验证,EGS模型的相对误差在3%以内。对于电池模型,以实验电流作为电池模型的输入,得到电池模型的端电压及SOC输出,结果表明,所建立的电池模型误差在可接受的范围内,电池电压和SOC的最大相对误差分别为3.5%和4.1%。
1.2 交通信号灯时序模型
面向动态交通流的信号灯有效通行时间估计是一个复杂的时空耦合问题,真实的驾驶环境中需要考虑道路上存在的大量车流、路口行人以及道路口车辆左右转向问题。本文所构建的系统面向车辆较少的城市场景,因此暂不考虑外界车流对完整绿灯可通行时间的占用问题,后期可通过预测外界车流的长度,相应地减少模型中绿灯信号的有效通行区间。
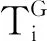
(10)
其中,j表示信号周期号,1和0分别表示信号灯为红灯和绿灯。出于安全考虑,黄色信号灯时间被归类为红灯代表的不可通行时间范围内。
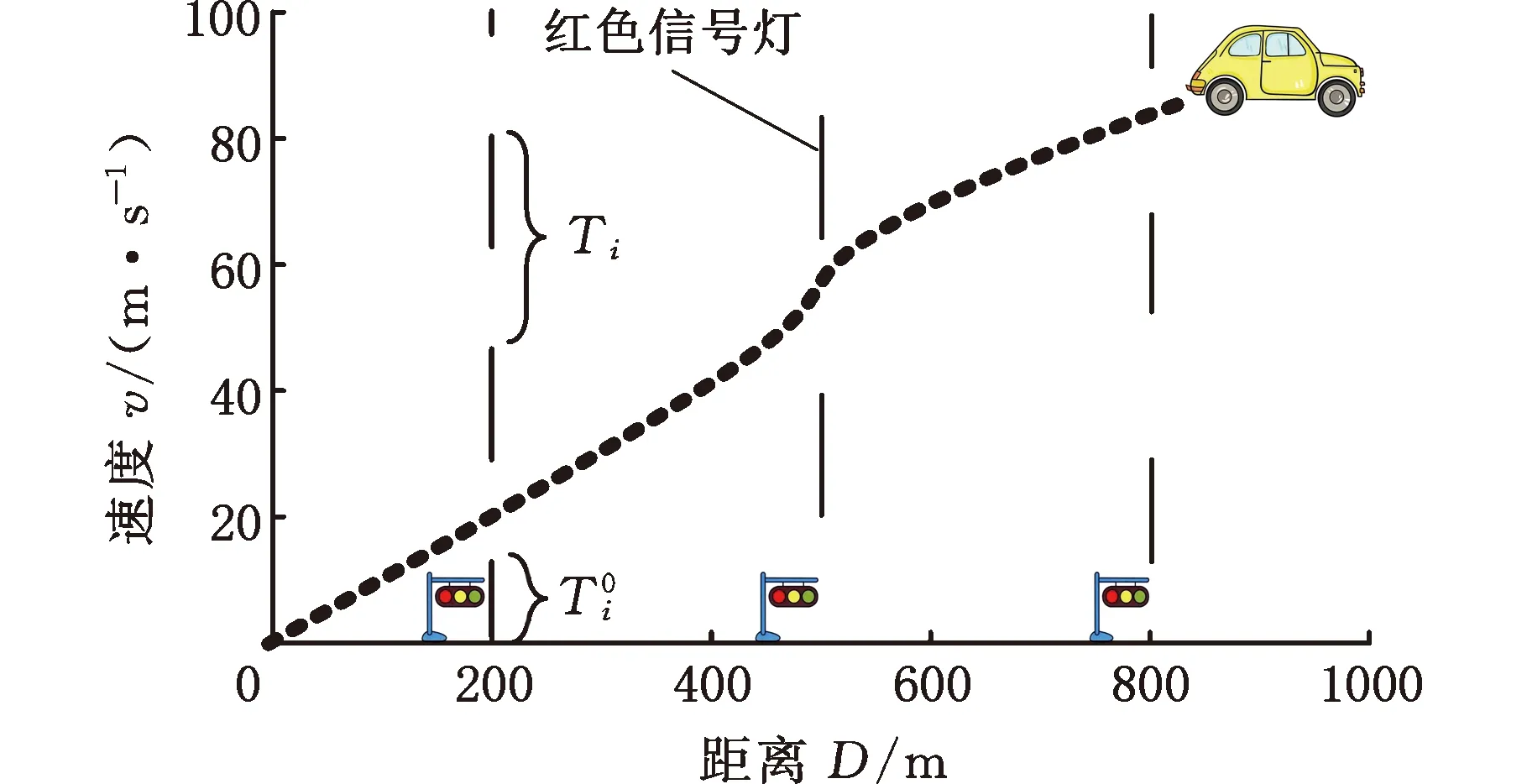
图4 城市道路多路口示意图Fig.4 Schematic diagram of multiple intersections of urban roads
道路车流的平均速度不一定是CAV最佳的节能驾驶速度,因此放宽车辆的行驶速度区间,对于同一个即将到达的路口,行驶速度决定了信号灯周期序号j,如图5所示信号灯序号j=1,2,3。当车辆到达路口遇到红灯时,约定其未来最近的绿灯时间窗口为其可通行的信号灯窗口,如图5中的信号灯序号j=1。
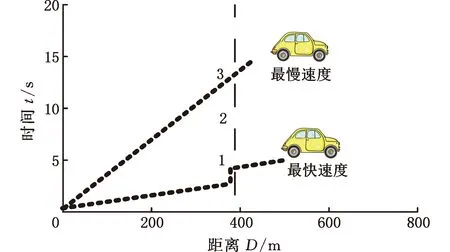
图5 车辆通行时间窗口示意图Fig.5 Schematic diagram of vehicle passable time window
在图4所示的场景中,假设对应每一区间段,车辆最大最小速度都得到2种信号灯周期数。不做任何速度优化时,对于连续3个路口,会得到2×2×2共计8种信号灯组合方案。为了提高全局优化算法遍历求解的效率,采用多核CPU并行计算的方式对多种组合方案同时进行优化求解,能大幅缩短算法的求解时间。
2 最优问题建模
图6为所提出的面向多连续路口场景的双层能量管理优化示意图。其中,左侧为第一层优化控制单元,对于车辆控制系统,信号灯信息决定了不同时间段道路的车流信息,车流信息决定了道路的平均车速。结合上述信息以及车辆自身状态,使用伪谱法规划获得车辆的最佳车速轨迹。图6右侧为第二层控制单元,根据规划的车速,同样使用伪谱法优化分配ESG和电池的功率比例。

图6 双层能量管理架构Fig.6 Double-layer energy management architecture
2.1 上层速度轨迹优化
针对某一确定的到达时间窗组合方式,系统优化目标是在确定的到达时间窗[t0,tf] 内使能源消耗最小化。因此,成本函数可以定义为
(11)
同时满足以下约束:
(12)
其中,ti表示通过第i个路口的时间;vi表示通过第i个路口时的车速。函数f表示车辆系统的动力学方程,其中的控制量u(t)在上层控制框架内为电机功率Pm。另外,车辆通行时间t和车速v均需要落在合理范围内。伪谱法的优势在于其可将连续交叉口通行问题转化为单信号灯路口速度规划问题,通过将多段规划问题的约束进行首尾拼接,以全局能耗最低为目标求解连续路口的能量管理问题。因此针对连续路口,在式(11)的求解过程中,还需要添加以下约束:
(13)
式中,d为每段道路的长度。
2.2 下层能量分配优化
上层得到的最优速度轨迹是下层能量管理的输入,下层通过将需求功率分配给EGS和电池,以使燃料消耗最小化。下层的目标函数可以表示为
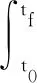
(14)
同时满足如下约束:
(15)
其中,fuel(Te,ne) 表示在转速ne和扭矩Te下的发动机瞬时燃油消耗率(即发动机的万有特性),X=(ne,SSOC,v)为状态向量,控制量u(t)在下层控制框架内为发动机节气门开度γ。式(15)中的第2式要求发动机的转速不出现超过Δn0的瞬态跳变;式(15)中的第3式要求车辆在行程结束时的SOC与初始SOC的变化量小于ΔSSOC,由于本文希望行程结束时的SOC与初始时基本一致,故取ΔSSOC=0.002。
常用的伪谱法有高斯伪谱法、Radau伪谱法和Legendre伪谱法[15]。与前两种方法相比,Legendre伪谱法具有计算方便的优点。因此,本文采用Legendre伪谱法求解上述策略优化的数值解。另外,由于运用Legendre伪谱法时需要对状态和控制变量进行离散化,常规的转化步骤如下:
(1)转换时域,将问题的定义时域[t0,tf]转换到时间区间[-1, 1]。
(2)离散化变量,将状态变量和控制变量在Legende-gauss-lobatto(LGL)配点处进行离散化处理,以形成N+1个离散的状态变量和控制变量,伪谱法仅在离散的配点处优化状态量和控制量,使用拉格朗日插值多项式近似实际的连续状态量和控制量。
(3)转化状态方程,将状态变量进行多项式参数化后,对状态的微分运算可以转化为对插值奇函数的微分运算。
(4)转化为线性函数,目标函数的积分项可通过Gauss-Lobatto积分方法计算。
(5)转化非线性规划问题,将原控制问题转化为以控制量和状态量为待优化变量的NLP问题。
本文采用文献[13]提出的LGL协调点方法对状态和控制变量作离散化处理。
3 数值仿真与分析
本节通过MATLAB仿真实验展示所提分层控制策略的性能。首先,建立了简单的三路口道路仿真场景,并假设初始车速v0=5 km/h,道路交通最低限速vmin=5 km/h,最大限速vmax=20 km/h。道路距离设置、信号灯时序时间和以及周期值设置见表1。用于对照的人工驾驶员以同样的初始状态驶入,设定相同的加速度与减速度值。此外,其他关键仿真参数中设定电池容量为30 A·h,电压等级330 V;发电机功率为20 kW,持续转矩60 N·m。考虑到实际工作中的启停过程燃油消耗量暂时无法估算,设定发动机不允许停机。由于HEV具有热管理系统,故本文未考虑温度变化对电池的影响。
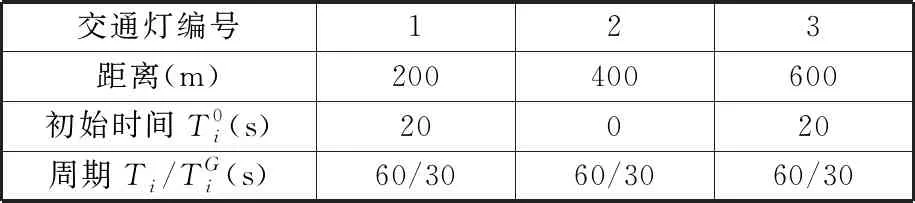
表1 仿真道路参数
图7所示为不同驾驶方式下的车辆行驶速度轨迹。可以看到,未经优化的人工驾驶员在每个路口都发生了较大的加速度变化。相反,经过伪谱法优化后的驾驶轨迹,车辆在加速到一定程度后并没有继续加大行驶速度。与人工驾驶速度轨迹相比,伪谱法优化的驾驶员以较低的速度通过第一个路口后才逐渐增大车速,以保证车辆在第二个和第三个路口时平稳通过。
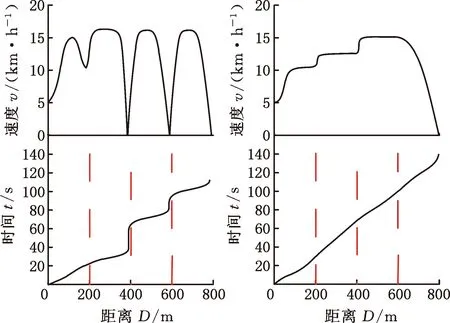
(a)人工驾驶 (b)PM优化图7 不同驾驶方式下的车速响应曲线Fig.7 Vehicle speed response curve under different driving modes

图8 连续10个信号灯场景下的SOC曲线Fig.8 SOC curve under 10 consecutive signal light scenarios

图10 连续10个信号灯场景下的功率分配结果(局部)Fig.10 Power allocation results under 10 consecutive signal lights scenario(partial)
由于仿真场景设置距离较短,消耗的能量变化较小,SOC曲线波动不明显,为此微调仿真参数,并设定将行驶工况修改为连续10个信号灯路口,总通行时间达到1000 s。图8~图10所示分别为采用伪谱法优化后的SOC轨迹、发动机工作点分布以及部分功率分配曲线。其中,图9中bfsc代表发动机比油耗,是指发动机每对外做功1 kW·h消耗的燃油量,其值越小说明发动机效率越高;图10中Pe为EGS功率输出,Pb为电池功率输出。
由图8可以看出,当终点目标SOC与初始值设定相同时,基于伪谱法的算法能够合理进行电池与EGS的能量分配,保证行程结束时的SOC值依然接近0.75。由图9的发动机工作点分布可以看出,3信号灯场景和10信号灯场景下,除了发动机转矩接近零的情况外发动机最佳工作点都在1800~2000 r/min之间的区域,该转速下的油耗最低,且发动机转矩基本能够接近最大值输出,由于发动机比油耗图也体现了效率的变化趋势,从图9中也能看出,优化后的发动机工作点沿着相似的效率梯度线变化。此外,针对连续长距离下的多个路口,控制策略使发动机在高效区域分布有较多的控制点,说明针对较长距离工况,本控制策略依然能有效地控制发动机维持在高效区。图10显示,大部分时间段电池与EGS输出功率接近,共同为系统提供能源,在部分时间段,EGS输出功率大于电池输出功率,此时EGS系统不仅提供车辆行驶的能源,同时在对电池进行充电。
为进一步展示SOC变化趋势,仿真修改SOC初始值为0.5,进行同样的测试,SOC变化如图11所示,结果的变化趋势与初始值0.75一样。当终点目标SOC与初始值设定相同时,基于伪谱法的算法能够合理进行电池与EGS的能量分配,保证行程结束时的SOC值依然接近0.5。

图11 50%初始值下的SOC变化Fig.11 SOC change at 50% initial value
统计两种驾驶模式下驱动电机消耗的总电量,人工驾驶和PM控制策略对应的电能消耗分别为0.2282 kW·h和0.2125 kW·h。相比人工自由驾驶的方式,基于伪谱法优化后的能量消耗平均节能率达到6.9%。为了进一步验证基于伪谱法的节能优化效果以及实时计算性能,针对相同的连续10个路口通行仿真场景,在上层得到最优速度曲线之后,下层能量分配优化过程中采用DP算法作为优化算法的对照基准,评价PM算法的优化性能。
对比优化后电池SOC变化如图12所示,可以看出,在SOC曲线中,DP算法优化得到的全局最优解开始时SOC主要呈下降趋势,在达到旅程一半左右时开始回升,DP优化结果最终也接近到达预设的初始值0.75。在大多数时候,基于PM算法优化得到的SOC曲线远高于DP法,这是两种算法的优化策略差异导致的,基于PM算法的优化策略是将每一段道路作为单一的优化方案,并通过连接整个道路阶段拼接而成,而对于DP算法,是从全局的角度计算整个工况周期内的最优解,因此虽然最终的SOC值比较接近,但是整个优化过程中,基于PM算法优化的结果严重偏离DP的最优解,这是两者的主要区别。
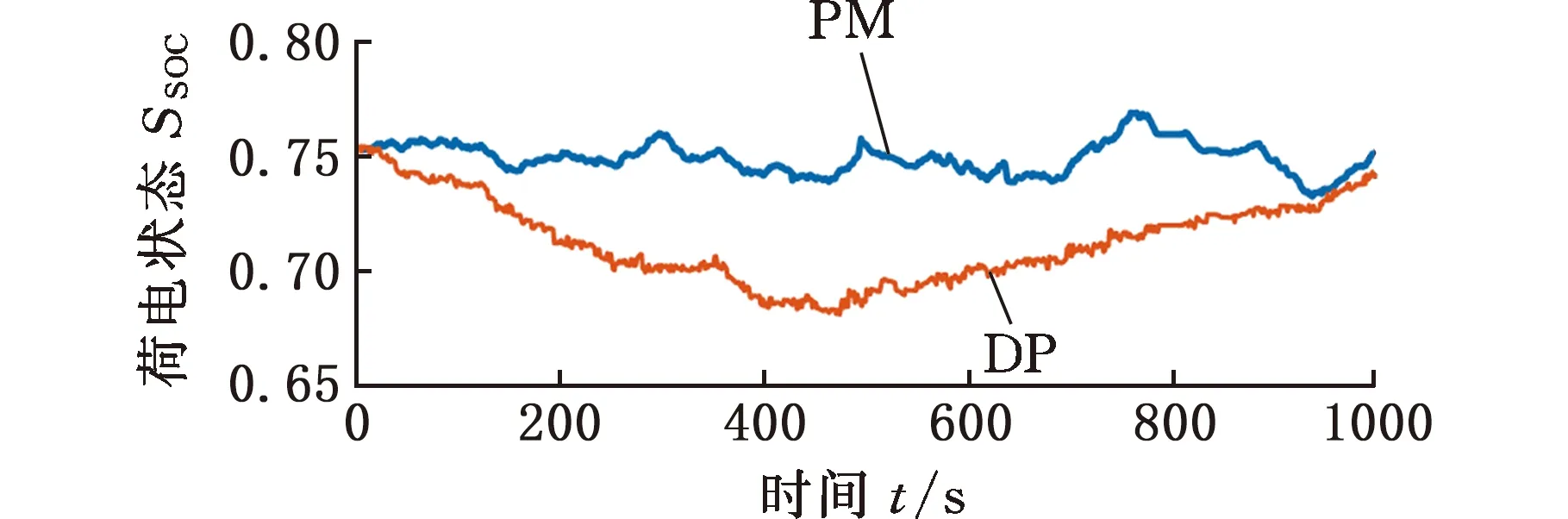
图12 连续10个信号灯场景下的SOC曲线Fig.12 SOC curve under 10 consecutive signal light scenarios
详细的油耗、SOC及计算时间统计结果见表2,由于SOC终点值均接近0.75,可通过油耗差距评价两者的性能差异。DP算法是业界常用的全局最优评价基准,相比之下,基于伪谱法优化的能耗水平可以达到DP算法的98%,且基于PM算法的平均计算时间(包括速度规划和能量分配两个环节)小于20 s,具有较强的实车应用潜力。

表2 两种不同算法下的油耗和计算时间
4 实车试验
本节通过实车试验与车载硬件控制系统共同验证所提策略的有效性,具体试验如下:受限于试验车辆条件,以及确保实车在最低安全风险下开展试验,试验中利用一辆联网的支持CAN总线驱动的智能车辆,如图13所示,在封闭的交通环境中模拟通过连续交叉路口。被控车辆一方面根据上层控制系统的速度规划合理通过交叉路口,另一方面实时采集车辆行驶状态数据,并将其作为下层控制策略的输入。同时,车载控制器执行硬件在环仿真分析,获得能量管理分配策略。车辆通过惯性导航设备获得车辆地理位置信息,并通过虚拟的交通信号时序来规划当前车辆的最佳行驶速度。

图13 实车试验平台与试验场地Fig.13 Real vehicle test platform and test site

图14 车辆速度规划驾驶结果Fig.14 Vehicle speed response following planned instructions
实车行驶速度结果如图14所示,根据设定的模拟交通信号,上层系统在车辆出发前规划给定全程建议速度,智能车辆通过总线控制车辆跟随规划速度行驶。从速度曲线可以看出,系统为了确保车辆顺利通过信号灯路口,每段道路都规划了不同的行驶速度。虽然车辆实际驾驶速度还无法完全达到规划值,但车辆速度变化趋势与规划速度完全一致,可以认为智能车辆有效地执行了上层系统规划的速度结果。实际跟踪误差可以理解为由车辆响应延迟与控制精度等因素导致。现场试验验证了分层能量管理中上层速度规划的有效性。
将采集的实车速度曲线作为下层控制策略的输入,利用车载工控机搭建下层控制系统执行能量管理算法,得到图15所示的发动机工作状态散点图。对比图15和图9中发动机在连续3路口下的发动机点分布可以看出,除了发动机转矩接近零的情况外,发动机最佳工作点都在1800~2000 r/min之间的区域,车载控制系统计算结果与模型仿真结果一致,可以推断下层算法得到的整体油耗较低。

图15 发动机工作点分布Fig.15 Engine operating point distribution
5 结语
本文提出了一种面向连续多路口交通场景的双层PM算法能量管理信息系统。首先,上层控制解决了考虑不同交通信号灯绿灯通行时间约束下的速度优化问题,进一步,下层控制基于PM算法将能量需求优化分配给EGS和电池。仿真结果表明,与未经优化的人工驾驶员相比,所提出的双层能量管理策略将燃油经济性提高了6.9%,且节能优化效果接近DP优化策略,同时基于PM算法的计算时间能满足实车使用要求。本文搭建了实车的部分驾驶试验,验证了控制策略在车载控制系统中应用的可行性。未来研究将进一步细化交通信号灯的建模过程,将该方法应用于实际道路的节能规划与在线实时优化控制中。

