推荐系统点击率预测模型

孟 露，王 莉

（辽宁科技大学 计算机与软件工程学院，辽宁 鞍山 114051）

随着互联网的不断发展，网络资源呈指数型增长，信息过载现象日益严重，如何高效获取符合需求的资源成为困扰人们的问题之一［1］。推荐系统能够对海量信息进行有效过滤与筛选，为用户推荐符合需求的资源，已成为人们日常生活中使用频率极高的应用［2］，广泛应用于电子商务、线上教育、新闻等个性化信息服务平台中［3］。推荐系统中点击率预测的效果会直接影响整体性能，是推荐系统最重要的环节。

深度神经网络在点击率预测方面取得很大进展。HFM（Holographic factorization machine）模型［4］使用循环卷积运算代替因式分解机的内积运算，对特征交互建模，但该模型与经典模型相对比，结构差别并不明显。AutoInt（Automatic feature interaction）模型［5］通过自注意力机制构造高阶交互特征，有效提升点击率预测的准确度，但注意力网络的训练过程较为复杂。FiGNN（Feature interactions graph neural network）模型［6］利用图神经网络的消息传递机制代替向量拼接，考虑特征之间的结构，便于学习高阶交互特征，但该模型参数量较大。ONN（Operation-aware neural networks）模型［7］对相同特征在交互过程中执行不同操作时的向量进行区分，但生成的嵌入向量维度较大。InterHAt（Interpretable hierarchical attention）模型［8］使用分层注意力网络提取重要的高阶交互特征，并引入自注意力机制做多重意义的交互，对预测结果提供解释，但计算复杂度较高。本文提出一种基于改进DeepFM（Deep factorization machine）的点击率预测LCFFM（Logarithmic conversion field-aware factorization machine）模型，能够充分利用特征信息，进行深层次特征交互，期望提升点击率预测的准确度。

1 特征交互及注意力机制

1.1 k阶特征交互

对于输入特征向量x∈Rn，k阶特征交互定义为g(xi,…,xp)。其中g(·)是特征组合函数，可以为内积、外积或哈达玛积等运算。当p≤2时，称为低阶特征交互，当p＞2时，称为高阶特征交互。特征经过组合后会提升与标签的相关性，如少儿与玩具、年轻人与娱乐设备、老年人与保健产品、健身教练与运动器材等，均为有相关联性的标签信息。由此可见，进行特征交互是十分必要的。

1.2 注意力机制

神经网络的注意力机制是将更多的资源分配给需要重点处理的目标，进而获取更多有价值的信息，并且极大程度上提高网络的训练效率。在推荐系统中利用点击率预测模型安排各项任务的优先级至关重要，引入注意力机制能够在大量特征中聚焦到对当前任务影响程度高的几项，降低或过滤冗余信息所带来的负面影响，进而提高模型的运算效率与准确性。

注意力机制的本质是寻址，实现过程分为信息输入、计算注意力分布和加权平均三个步骤［9］。第一阶段将给定任务的查询向量输入到模型中；第二阶段通过计算向量点积表示两个向量之间的相关度，采用softmax函数计算注意力权重；第三阶段计算输入信息的加权平均，用注意力分布解释信息间的相关程度。

2 LCFFM模型结构

LCFFM模型由特征输入、特征嵌入、低阶特征交互、高阶特征交互和点击率预测五部分组成，具体结构如图1所示。

图1 LCFFM模型结构Fig.1 Structure of LCFFMmodel

2.1 特征输入

在点击率预测问题中，输入数据由稀疏的数值特征和分类特征组成，将所有输入数据串联起来，表示为

式中：m是特征的总数量；xi是第i个特征的输入。

2.2 特征嵌入

由于输入的特征采用One-hot编码，使样本空间扩大数倍，而神经网络对于高维稀疏数据训练效率极差，因此需要将输入数据进行稠密化处理

式中：ei是嵌入向量；Vembed∈Rdi×de为对应的嵌入矩阵，di和de分别表示第i个特征xi的大小和其对应嵌入向量的大小。

稠密化处理本质上属于一种映射表查询机制，利用拓扑不变性原理，将离散数据所属的高维度特征空间映射到低维稠密特征空间中，保留原始数据的信息并具有可解释性。其主要目的是把网络中的每个节点映射到一个固定维度的空间中，同时这些向量还能反映网络中的关系。

采用SENet（Squeeze-and-excitation networks）注意力机制学习特征重要程度的权值，学习过程主要分三个步骤。

首先是压缩阶段，对每个特征嵌入向量进行数据压缩，重新构建特征的信息组合，从而得到一个新的全局特征统计向量Z={z1,z2,…,zi}，其中

式中：zi表示第i个特征的全局信息；ei为嵌入向量；k为组合中特征个数。

其次是激励阶段，为每个特征学习一个相对应的权重向量A={a1,a2,…,am}，用来表示特征重要程度。为了降低模型复杂度并提升泛化能力，这里采用包含两个全连接层的沙漏型结构，第一层的作用是降低纬度，第二层的作用是恢复原始维度。其中，注意力权重的计算式

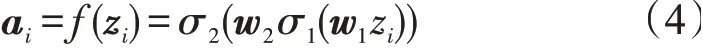
式中：σ为非线性激活函数；w1和w2为两个要学习的参数。

最后是重构阶段，把学习到的m个注意力权重向量与原始特征嵌入向量进行逐元素相乘，输

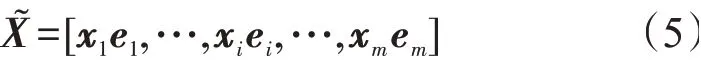
新的向量与原始输入向量具有相同的维度，但其包含特征重要性权重，对高价值特征进行加强，提升学习效果，并且抑制重要性低的特征和噪声数据，更有利于模型对不同特征进行区分。

2.3 低阶特征交互

利用FFM（Field-aware factorization machine）学习特征的一阶项和二阶交叉项，引进特征域感知概念，使模型的表达能力更强。计算式

式中：x为特征向量；w为权重向量。

FFM与FM的区别在于隐向量由原来的wj1变成了wj1,f2，这意味着每个特征对应的隐向量不是一个，而是一组。当特征xj1与特征xj2进行交叉时，xj1会从xj1这一组的隐向量中挑选出与xj2的域f2对应的隐向量wj1,f2进行交叉。同理，xj2也会用与xj1的域f1对应的隐性量进行交叉。

2.4 高阶特征交互

在高阶特征交互阶段，首先利用对数转换结构学习交叉特征中每个特征的幂（即阶数），然后堆叠多个隐藏层捕获信息。

对数转换结构将输入转换为对数空间，将乘法转换为加法，将除法转换为减法，将幂运算转换为常数乘法。这种转换方法能够在不改变数据性质和关系的前提下缩小变量的尺度，使数据更加平稳，方便计算，并弥补了前馈神经网络表达能力不足的缺点。该结构由多个对数神经元组成，其中每个对数神经元表示为

通过多个对数神经元学习交互特征中每个特征的幂，进而确定特征交互的阶数。第j个对数神经元的输出可表示为

式中：wij表示第j个对数神经元输入的第i类特征嵌入向量的权重；exp()和ln()表示相应向量的求导和取对数运算。

由于取对数操作的取值范围是(0,+∞)，因此需要在输入时加上一个极小的正数，以保证各项输入均为正值。

在对数转换结构后堆叠了多个隐藏层。首先将所有的交互特征连接起来作为前馈神经网络的输入

其中N是前一层中对数神经元的数量。将z0输入到L个隐藏层中

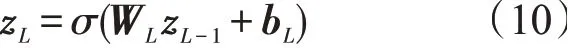
式中：WL表示第L层的权重矩阵；bL表示偏置向量；σ为激活函数，用于捕捉非线性特征交互。

2.5 点击率预测

LCFFM模型中，低阶特征交互与高阶特征交互两部分为并行结构，因此先对二者做线性组合，经Sigmoid函数处理，得到点击预测结果

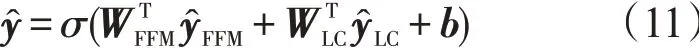
式中：和分别表示低阶和高阶特征交互模块的权重；b表示模型的总体偏差；σ选用Sigmoid激活函数，其输出结果在0到1之间，便于点击率预测效果的判断。

3 模拟实验

3.1 数据集及预处理

实验采用Avazu广告数据集，由按时间顺序排列的广告点击数据组成，共有4 042万个样本。每个样本有24个变量，均为类别型特征，有广告、用户和设备的属性。其中label=1表示该条广告被用户点击，label=0表示该条广告未被用户点击。

Avazu广告数据集包含的数据量较大，其中存在较多的噪声数据，因此需要对数据进行预处理，使模型可以更好地学习特征及特征之间的规律。采用Min-Max标准化方法将特征数据的取值范围进行缩放，对特征数值x1,x2,…,xn进行变换，将其映射到[0,1]的范围中，令yi=[y1,y2,…,yn]∈[0,1]，则

这种归一化操作使特征在一个区间内表达，消除特征之间的量纲影响，同时可以加快模型的收敛速度。

3.2 实验环境与评价指标

编程语言为Python，机器内存为128G，操作系统 为Ubuntu16.04，处 理 器 为Intel Xeon（R）Bronze3104，显卡为Nvidia Titan Xp（Pascal），硬盘为512G SSD+4T×2，并且采用PyTorch1.7.1框架。

点击率预测为二分类问题，使用AUC（Area under curve）和对数损失（Logloss）两个指标对LCFFM模型效果进行评估。

AUC是机器学习中广泛应用的评价指标，它用坐标系中ROC（Receiver operating characteristic）曲线与x轴之间的面积作为结果，对二分类问题的预测效果进行比较。AUC值通常介于0.5～1之间，其值越大，模型的分类效果越好，预测越准确。

对数损失亦称交叉熵损失，能够反映预测结果的平均偏差，计算式

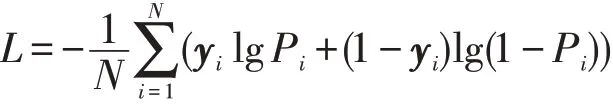
式中：N为输入的样本总数；yi为第i个样本的真实值；Pi为输出层计算出的概率。

对数损失测量每个样本真实与预测分数之间的距离，其值越小，模型的损失越小，预测的性能越好。

3.3 模型超参数分析

（1）隐藏层层数。隐藏层的层数是深度学习神经网络中一个至关重要的部分。LCFFM模型在训练过程中，将隐藏层层数设置为1～5进行实验，结果如表1所示。当隐藏层层数为3时，AUC值最大，Logloss值最小，表明此时模型表现最好。同时说明当深度神经网络可挖掘到有效信息时，想进一步提升点击率预测效果，通过增加网络的深度，在训练成本方面可能会消耗过大，而且层数过多的网络很容易出现过拟合现象。

表1 不同隐藏层层数的效果Tab.1 Effects of different hidden layers

（2）丢弃率设置。丢弃率（Dropout）是指神经元保留在网络中的概率，其作为一种正则化技术，可以有效防止或降低过拟合现象。LCFFM模型在训练过程中，将丢弃率设置为不同的值进行实验，结果如表2所示。当丢弃率为0.5时，AUC达到最大值，Logloss达到最小值。这表明在每一轮训练的过程中，随机地让一半数量的神经元参与到模型中，会得到较好的预测效果。

表2 不同丢弃率的效果Tab.2 Effects of different dropout rates

（3）激活函数。对采用深度学习技术的模型，激活函数通过加入非线性因素使数据线性可分，能够解决较为复杂的问题，同时也为神经网络的反向传播带来可能。LCFFM模型在训练过程中，选择Sigmoid、Tanh与Relu三种常用的激活函数分别进行实验，结果如表3所示。采用激活函数Relu时，AUC和Logloss指标均达到最佳。与Sigmoid和Tanh相比，Relu不需要链式求导，也不会发生梯度饱和，并且其计算复杂度较低，更适合反向传播求导。

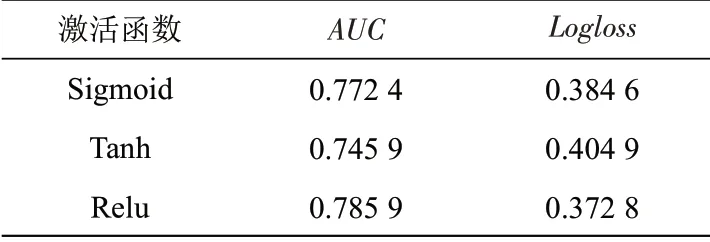
表3 不同激活函数的效果Tab.3 Effects of different activation functions

（4）优化器。使用优化器能够在一定程度上优化模型参数，使预估值不断逼近真实值，从而达到最小化损失函数的目的。LCFFM模型在训练过程 中，选 择Momentum、RMSProp（Root mean square prop）、SGD（Stochastic gradient descent）与Adam（Adaptive momentum estimation）四种常用的优化器分别进行实验，结果如表4所示。采用Adam得到的AUC和Logloss值均优于其余三个优化器，因其在每一次训练过程中，使用的学习率都有一定的范围，有利于模型收敛。

表4 不同优化器的效果Tab.4 Effects of different optimizers

3.4 实验结果与分析

LCFFM模型最优参数设置：批量大小设为4 096，L2正则项参数设为0.000 1，学习率设为0.001，激活函数选择Relu，优化器选择Adam，隐藏层层数设为3，神经元丢弃率设为0.5，隐藏层的神经元数目设为256，数据迭代训练次数为10。

将LCFFM模型分别与FM、FFM、LR（Logistic regression）、LR+GBDT（Gradient boosting decision tree）四个传统点击率预测模型，以及FNN（Factorization neural network）、PNN（Product-based neural network）、Deep Cross、NFM（Neural factorization machines）、AFM（Attentional factorization machines）、DeepFM、AutoInt（Automatic feature interaction）七个基于深度学习的点击率预测模型进行对比实验。结果如表5所示。表中实验结果为5次实验的均值。

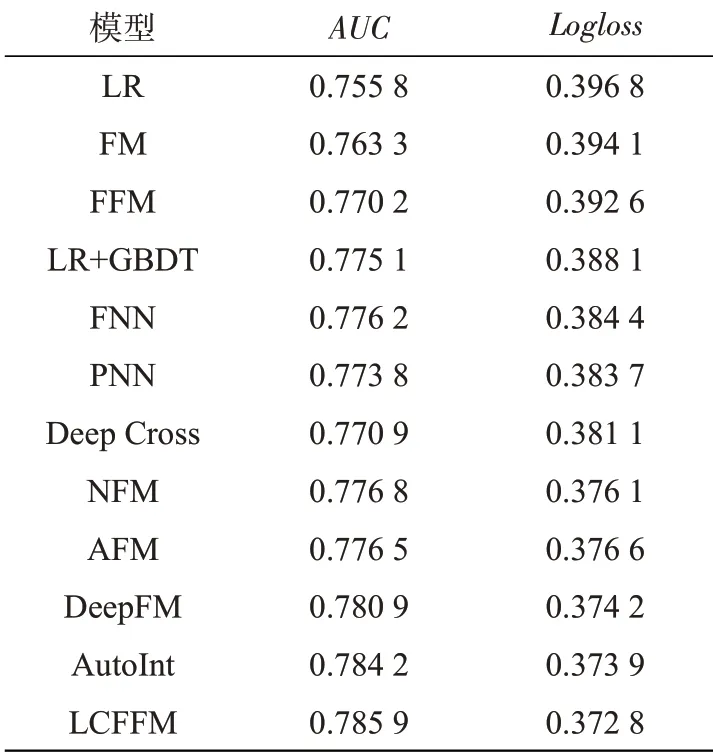
表5 模型效果对比Tab.5 Comparison between results of different models

与四个传统模型相比，LCFFM模型在Avazu数据集上的AUC达到0.785 9，提升了1.08%到3.01%，Logloss达到0.372 8，降低了1.53%到2.4%；与深度学习模型相比，LCFFM模型的AUC提升了0.17%～0.97%，Logloss降低了0.11%～1.16%，均得到最优效果。在推荐系统的点击率预测研究领域，AUC微小的提高通常被认为具有重要意义，因为平台拥有庞大的用户群，微小的提升就能带来收入大幅的增长。

实验结果表明，利用注意力机制计算并区分不同特征对预测结果的影响程度，能够抑制噪声数据。结合域因式分解机和对数转换结构对特征组合进行探索，挖掘特征之间的相关性，能够强化模型的记忆能力，同时增强其表达能力，从而使点击率预测的准确度得到进一步提升。

4 结论

本文提出LCFFM模型预测点击率。首先，在特征嵌入阶段加入SENet注意力机制，动态学习不同特征的重要性，抑制低频或无效特征的影响。其次，利用特征域因式分解机学习低阶特征交互，同时融合对数转换结构与前馈神经网络学习高阶非线性特征交互，将特征组合中每个特征的幂作为要学习的系数，在强化模型泛化能力的同时，增强其表达能力。最后，通过Relu函数处理，得到点击率预测结果。

对比实验结果显示，本文的LCFFM模型AUC达到0.785 9，Logloss达到0.372 8，均比现阶段点击率预测模型的效果有所提升。这表明模型通过计算并区分不同特征对预测结果的影响程度，并从多角度进行特征交互，可以有效提升点击率预测的准确度，同时有较强的抗噪能力。该模型适用于现实生活的点击率预测任务，具有较高的扩展性和实用性。