大落角机动目标逆轨拦截最优滑模制导律设计

周梦平, 孟秀云, 刘俊辉

(北京理工大学宇航学院, 北京 100081)

0 引 言

在战场上，为了获得更好的对阵地打击效果,往往会要求火箭弹与制导炮弹具有较大落角，对阵地进行攻击,同时火箭弹与制导炮弹在弹道末端通常具有较大的速度。这种在弹道末端具备大落角与较高速度的目标,是阵地防空中的一大难题。为提高拦截概率,拦截弹可以采用逆轨拦截的方式进行迎面拦截。逆轨拦截时,导弹速度与弹目视线重合,导弹的法向过载与弹目视线垂直,能使导弹在制导末段具有较充裕的机动能力。

逆轨拦截问题可以看成是终端攻击角约束问题,在具有终端角度约束的末端制导律设计中,应用最多的为变结构控制和最优控制思想。

文献[7]最先将滑模变结构控制应用于空-空导弹的目标拦截问题,设计了以比例导引为基础的滑模面。文献[8]将目标的加速度认为是不确定项,采用变结构方法进行制导律设计。文献[9]推导了一种带落角约束的无奇点快速终端滑模制导律,并设计了非线性扰动观测器，对扰动进行动态补偿。文献[10]提出了一种时变全局滑模控制方法,通过线性扩张状态观测器估计目标的加速度,推导了针对具有加速度机动目标的攻击角约束制导律。文献[11]将目标加速度信息作为扰动进行观测补偿,提出了一种考虑加速度饱和的落角约束制导律。考虑导弹自动驾驶仪的动态特性,文献[12]基于滑模控制设计了角度约束制导律,文献[13]提出了一种用于三维目标拦截的输出反馈连续终端滑模制导律。针对非解耦的三维拦截问题,文献[14]基于时基发生器函数提出了一种时变的滑模制导律,在满足终端角度约束的同时实现视线角的有限时间收敛。

最优控制理论在制导律的设计中能够综合考虑各种约束,得到了广泛应用。文献[18]基于碰撞几何提出了一种适用于顺/逆轨拦截的最优制导律。文献[19]对具有加速或减速的目标给出了统一的最优制导律。文献[20]将与剩余飞行时间相关的函数作为性能指标,基于最优控制理论推导了带落角约束的最优制导律。文献[21]利用最优控制和微分对策理论,对任意阶线性导弹动力学模型推导了具有角度约束的制导律。文献[22]考虑导弹速度时变的情况,基于间接高斯伪谱法设计了带有攻击角度约束的最优中制导律。文献[23]考虑导弹自动驾驶仪二阶动态特性,采用高斯伪谱法设计了多约束条件下的三维最优中制导律。文献[24]基于最优控制理论提出了一种同时具有攻击角约束和攻击时间约束的制导律,并解决了歧义性问题。文献[25]提出了一种考虑攻击角度约束和终端加速度约束的最优制导律,并且对导弹自动驾驶仪动态的不确定性具有一定鲁棒性。

结合最优控制方法和变结构控制方法,文献[26]基于视线角速度提出了最优滑模制导律,能够对目标机动有较强的鲁棒性。文献[27]考虑目标机动和导弹自动驾驶仪特性,基于非奇异终端滑模面,利用状态依赖黎卡提方程提出了最优滑模制导律。文献[28]设计了一种带落角约束的再入机动弹头的复合导引律,该导引律在最优导引律的基础上引入滑模变结构控制,增强导引律的鲁棒性,并采用神经网络自适应调节增益。文献[29]考虑高度误差,选取误差作为切换函数,设计了带有攻击角约束的最优滑模制导律。文献[30]提出了一种具有自适应滑模项的最优滑模制导律,提高了控制精度,解决了目标追踪中的滞后问题。

但这些最优滑模制导律多数是基于零化导弹与目标的视线角速度来设计的,并且没有基于李雅普诺夫稳定性理论对参数的设计进行分析。本文提出的逆轨拦截最优滑模制导律基于目标预测弹道,采用扩张状态观测器对目标弹道倾角进行估计,基于李雅普诺夫稳定性理论设计了参数的变化函数。最后，通过仿真分析对本文提出的制导律的性能进行验证。

1 弹目相对运动方程

为了进行制导律设计,首先建立弹目相对运动方程。通常情况下,弹目相对运动关系可以解耦成俯仰和偏航两个平面上的运动,本文将在纵向平面内建立弹目相对运动方程,并进行制导律的设计。

弹目相对运动关系如图1所示。

图1 弹目相对运动关系Fig.1 Relative motion relationship between missile and target

图1中，与分别为导弹与目标的速度,与分别为导弹与目标的弹道倾角,0为初始时刻目标弹道倾角,与分别为导弹和目标的法向加速度,Δ为导弹到目标预测弹道的距离。由图1可以推导出:

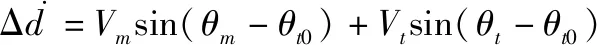
(1)

式中:与分别为导弹与目标的速度大小。

对式(1)进行求导:

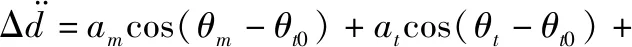
(2)

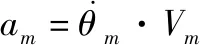
(3)

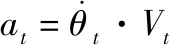
(4)

式中:与分别为导弹和目标的加速度大小。

将导弹与目标的速度大小视为常值,式(2)化简为

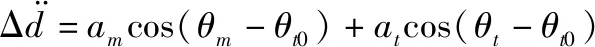
(5)

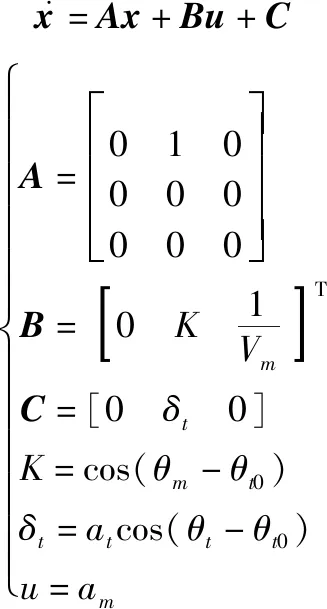
(6)

2 攻击角约束最优滑模制导律设计

2.1 攻击角约束最优制导律设计

将逆轨拦截的需求转化成对导弹攻击角的约束,基于最优理论进行带攻击角约束的最优制导律设计。

选择脱靶量、攻击角和控制能量作为最优性能指标,设计性能指标函数:

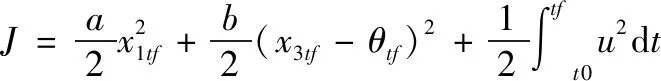
(7)

式中:,为脱靶量与攻击角的权重系数;为角度终端约束,当目标无加速度机动时=0,表示终端时刻。根据上述性能函数,得到其哈密顿函数:

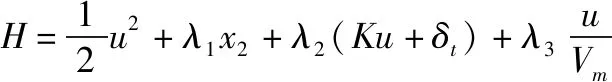
(8)

协态方程与横截条件:

(9)

由式(9)推导可得

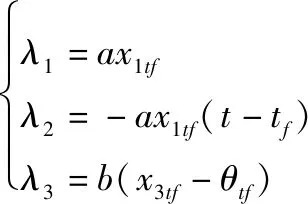
(10)

根据极小值原理可以得到控制方程:

(11)

式中:1,3为终端项;记=-,为剩余飞行时间。根据线性系统理论,线性时变系统非齐次状态方程的解为

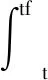
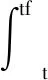
(12)

若不考虑目标做加速度机动,可以忽略式(12)右端第3项。根据式(12)可以得到终端项1,3的表达式:

(13)

式中:(,)为状态转移矩阵,满足如下微分方程:

(14)

根据级数近似法

(15)

将式(13)右端第2项展开:

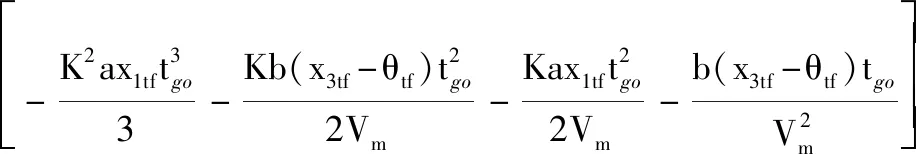
(16)

为了计算控制方程式(11)中的终端量1,3,定义新的变量:零控脱靶量(zero effort miss, ZEM)和零控角误差(zero effort angle error, ZEAE)。

(17)

将式(16)与式(17)代入式(13)中，整理得到

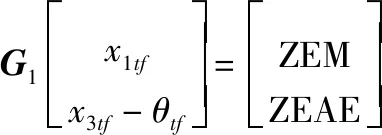
(18)

其中

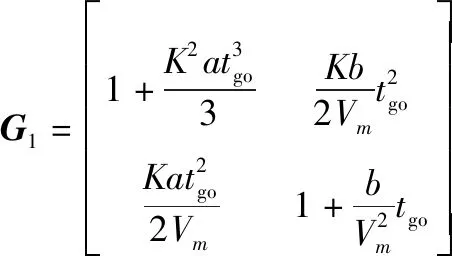
根据式(17)可以得到:

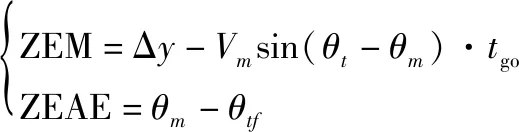
(19)

由式(18)与式(19)即可解得终端量1,3,将其代入式(11)，即可得到制导律表达式。

2.2 攻击角约束最优滑模制导律设计

最优制导律具有较好的动态性能,但是对于系统参数摄动和外界干扰的鲁棒性较差,而滑模制导律具有较强的抗干扰能力,因此将二者结合,设计一种对目标机动具有较强鲁棒性、同时具有较好动态特性的新型制导律。

221 滑模制导律设计

为了满足导弹对脱靶量与攻击角约束的要求,将弹目距离、攻击角作为控制目标,即=0,=,因此设计如下滑模面:

=+(-)

(20)

对式(20)进行求导:

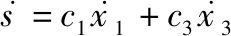
(21)

选取幂次趋近律:

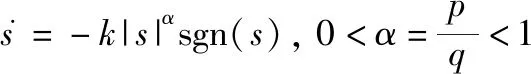
(22)

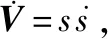
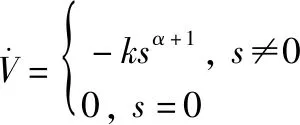
(23)

其中

(24)

结合式(6)、式(21)和式(22),经整理，可以得到控制律的表达式:

(25)

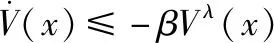
(26)

式中:=(+1)2=(+)2。那么在≠0时,满足()>0,式(26)可变形为

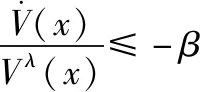
(27)

对式(27)从飞行过程中时刻到系统稳定时刻积分:

(28)

式中:表示时刻系统的状态量。由式(28)可知系统是在有限时间内收敛的。式(28)中，-可以用预估剩余飞行时间代替。则可将取为

(29)

(30)

从式(30)可以看出系数能随系统的状态变化而变化,增加了制导律的鲁棒性。

222 最优滑模复合制导律设计

将第21节中式(11)给出的最优制导律记作,式(25)给出的滑模制导律记为。选取最优趋近律

(31)

式中:为需要设计的参数,满足∈[0,1]。将式(21)与式(31)联立可得

=+(1-)

(32)

通过设计式(31)的最优趋近律,得到了形如式(32)在工程上常用的最优与滑模的加权融合的复合制导律。在后文会基于李雅普诺夫稳定性理论对该制导律进行稳定性分析,并给出参数的设计思路。

所设计的制导律用到了目标的弹道倾角,下文将基于扩张状态观测器对目标弹道倾角进行估计。

2.3 基于扩张状态观测器的目标弹道倾角估计

由式(11)与式(20)可知,最优制导律与滑模制导律均包含终端角约束,而即为终端时刻目标的弹道倾角,在实际工程中往往无法测量目标的弹道倾角信息,因此需要对目标的弹道倾角进行估计。

根据弹目运动相对关系(见图1),考虑如下系统:

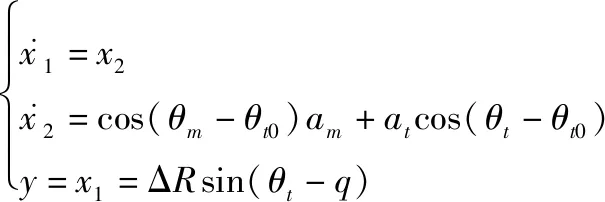
(33)

式中:为系统的输出;Δ为弹目相对距离;为弹目视线高低角。实际中,由于未知,将其视为扰动,均由0进行代替。

设计如下扩张状态观测器:

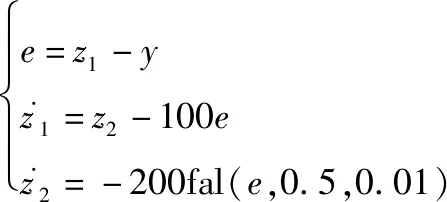
(34)

其中,

(35)

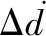
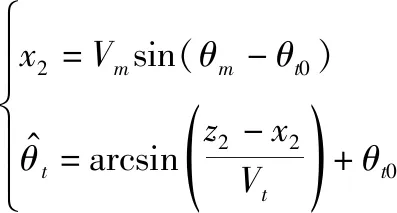
(36)

3 最优滑模制导律稳定性分析

首先选取广义能量函数=2,为表述方便,记=,是时变的。那么式(21)可以化为如下形式:

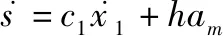
(37)

对广义能量函数求导:

(38)

第22节已分析了式(38)右端第2项的稳定性,因此这里仅关注右端第一项,并将其记作。

最优制导律在制导初期阶段,往往拥有较小的过载指令,且指令变化较为平缓;而基于幂次趋近律设计的滑模制导律在制导初期往往具有较大的过载指令,且指令变化较快。根据制导初期阶段最优制导律与滑模制导律各自的特点,进行如下假设。

在初始一定时间内,独立设计的最优制导律与滑模制导律产生的指令符号相同,均能使导弹接近目标的预测弹道,且满足||<||。

根据式(32)与假设1,当∈[0,]时,可将最优制导律写作,是时变的,且满足0<≤1。经过上述处理,可得

(39)

将式(39)代入式(38)中,可得

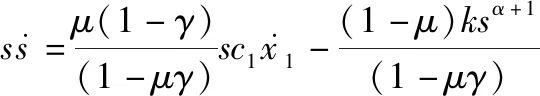
(40)

为了得到关于参数的设计思路,再次选取广义能量函数:

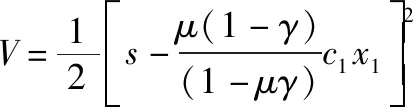
(41)

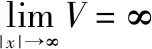
(42)

结合式(32)和=,对式(42)进行化简:

(43)

式中:由所设计的最优制导律与滑模制导律的特性决定,记=,有∈(0,1]。对式(41)求导并结合式(40),可得

(44)

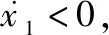
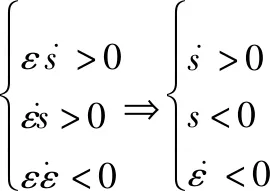
值得注意的是当满足式(45a)与式(45b)时,系统显然是稳定的,而根据式(45c)可以得到参数的设计思路。

对式(45a)展开:

(46)

由于∈[0,1],因此式(46)右端大于1即可。式(46)变形为

(47)

对于式(45b)有:

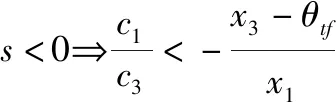
(48)

结合式(47)和式(48)可以得到参数,的选取原则。

而式(45c)与需要设计的时变系数和最优制导律与滑模制导律的特性有关,因此可以根据式(45c)进行参数的设计,以提高系统的稳定性。将式(45c)展开:

(49)

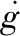
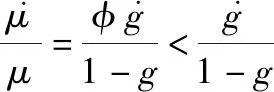
(50)

对式(50)等式两端同时积分:

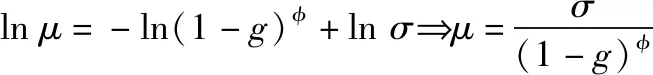
(51)

式中:,为可调节系数,>1,>0。参数的选择应保证∈[0,1]和的连续性。

(52)

经过上述分析,按照式(52)给出的表达式进行参数的选取,能够保证系统的稳定性。

4 仿真分析

4.1 仿真条件

为验证本文设计的最优滑模制导律的性能,考虑目标有加速度机动与目标无加速度机动两种情况,将本文设计的滑模制导律、最优制导律和最优滑模制导律进行对比仿真分析。

仿真条件1:导弹飞行速度为250 m/s,初始弹道倾角为20°,目标初始位置为(6 000 m,12 000 m),目标初始弹道倾角为-70°,目标速度为600 m/s。

仿真条件2:导弹飞行速度为250 m/s,初始弹道倾角为20°,目标初始位置为(5 000 m,12 000 m),目标初始弹道倾角为-70°,目标速度为600 m/s,目标有常值法向加速度-5 m/s。

4.2 仿真结果与分析

在仿真条件1下,对所设计的制导律进行数学仿真。图2为3种制导律下的导弹弹道曲线,图3为导弹弹道倾角变化曲线,图4为导弹加速度指令曲线,图5为函数变化曲线。

图2 3种制导律弹道曲线Fig.2 Trajectory curves of three guidance laws

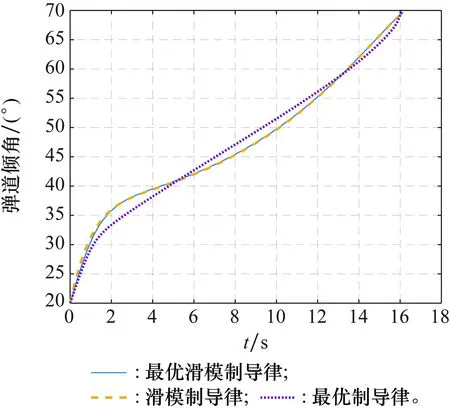
图3 3种制导律弹道倾角曲线Fig.3 Trajectory inclination angle curves of three guidance laws

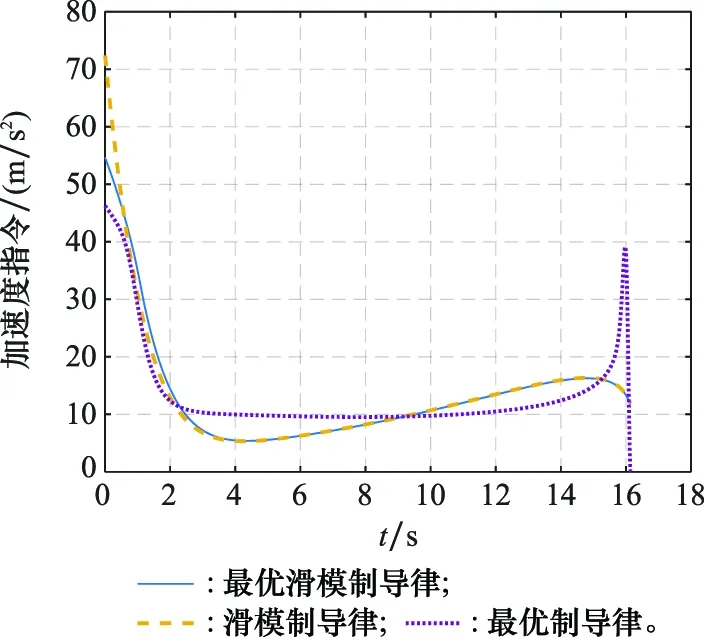
图4 3种制导律加速度指令Fig.4 Acceleration commands of three guidance laws

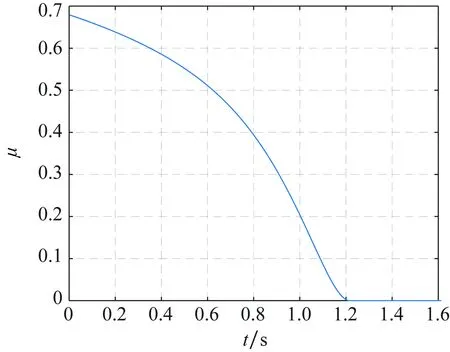
图5 μ函数变化曲线Fig.5 Curve of μ function

图2与图3的仿真结果表明,3种制导律均能击中目标并达到期望的弹道倾角。表1列出了3种制导律在终端时刻的弹道倾角和脱靶量。

表1 3种制导律脱靶量与弹道倾角比较Table 1 Comparison of miss distance and trajectory inclination angle of three guidance laws

从表1可以看出,在攻击匀速目标时,3种制导律的弹道倾角与期望倾角偏差均较小,但最优滑模制导律与滑模制导律的脱靶量要明显小于最优制导律。

图3的仿真结果表明,滑模制导律在初始阶段具有较大的加速度指令,制导末期指令较为平稳;最优制导律初期指令较小,制导末段指令出现了较大幅度的波动。最优滑模制导律的初期指令介于最优制导律与滑模制导律之间,而在制导末期完全切换到了滑模制导律,避免了最优制导律制导末段的指令波动问题。图4的仿真结果表明,本文所设计的函数具有较为平稳的变化过程,说明了第3节分析的正确性。

在仿真条件2下,对所设计的制导律进行数学仿真。图6为3种制导律下的导弹弹道曲线,图7为目标弹道倾角观测值与真实值,图8为导弹弹道倾角变化曲线,图9为导弹加速度指令曲线,图10为函数变化曲线。

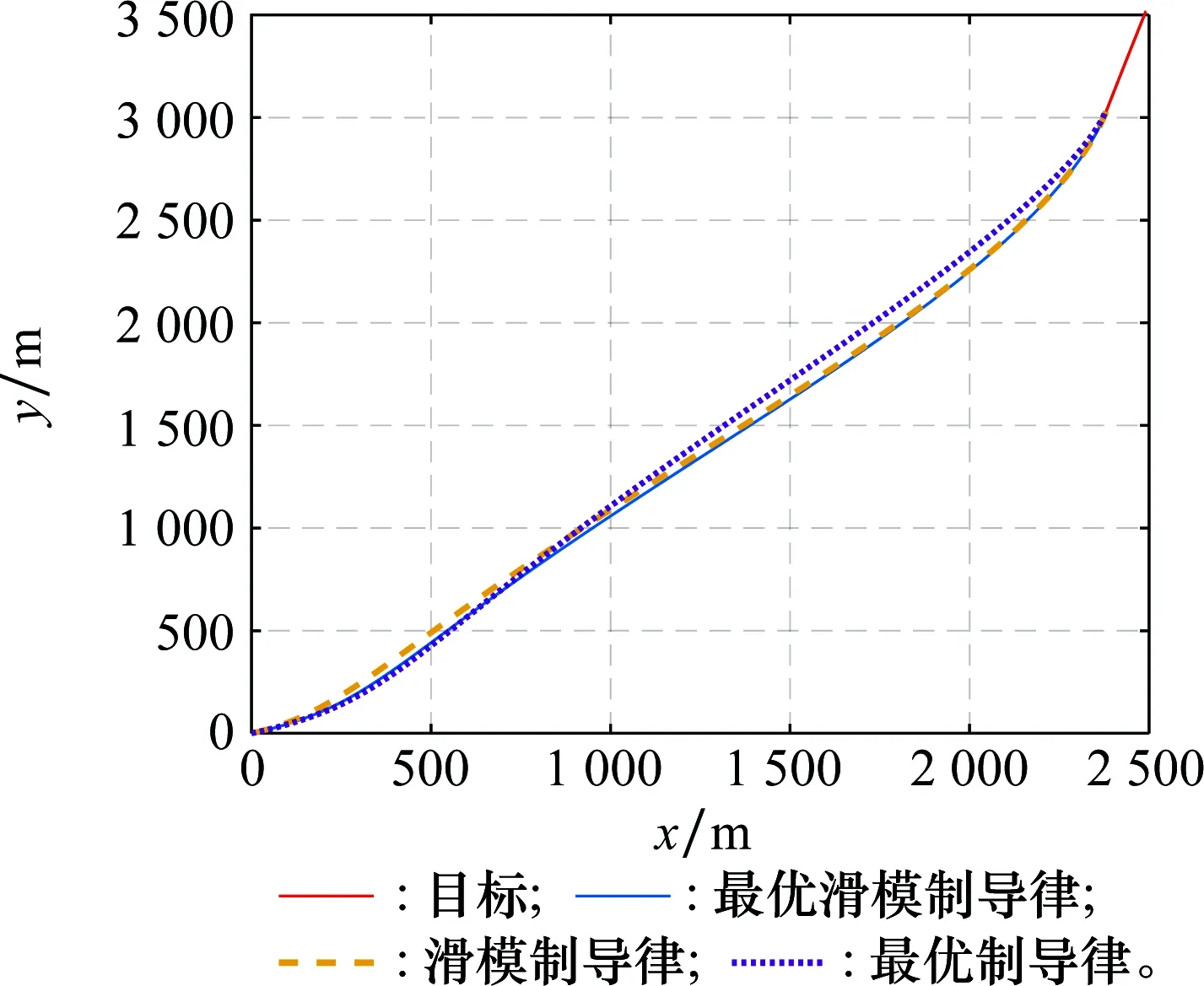
图6 针对加速度目标3种制导律拦截弹道Fig.6 Interception trajectory curves of three guidance laws against accelerated target

图7 目标弹道倾角观测值与真实值Fig.7 Observed and true values of target ballistic inclination angle

图8 针对加速度目标3种制导律弹道倾角曲线Fig.8 Trajectory inclination angle curves of three guidance laws against accelerated target

图9 针对加速度目标3种制导律加速度指令Fig.9 Acceleration commands of three guidance laws against accelerated target

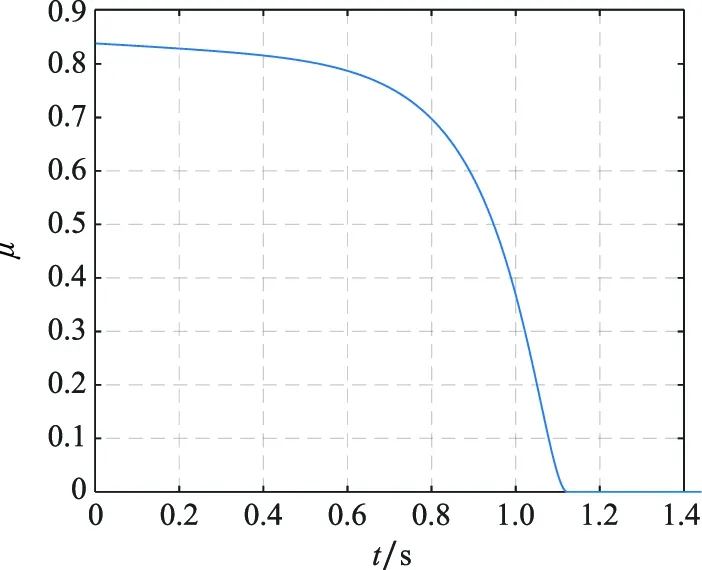
图10 针对加速度目标μ函数变化曲线Fig.10 Curve of μ function against accelerated target

由图6～图8的仿真结果可知,3种制导律在拦截具有法向加速度的目标时,均能够击中目标,并能达到期望的弹道倾角。由图7可以看到,对目标弹道倾角的观测值能够迅速收敛到真实值附近,本文采用的扩张状态观测器能够较为准确地估计目标的弹道倾角。表2列出了3种制导律在攻击加速度机动目标时终端时刻的偏差角(导弹弹道倾角+目标弹道倾角)和脱靶量。

表2 针对加速度目标3种制导律脱靶量与偏差角比较Table 2 Comparison of miss distance and trajectory inclination of three guidance laws against accelerated target

由表2可以看出,在攻击有加速度机动的目标时,最优制导律的脱靶量与偏差角均较大,制导精度有所降低。而最优滑模制导律与滑模制导律的脱靶量与偏差角均较小,制导精度较高,但最优滑模制导律的脱靶量要明显小于滑模制导律,说明了最优滑模制导律的优越性。

图9的仿真结果表明,滑模制导律在攻击有加速度机动的目标时,在初始阶段加速度指令过大,但其制导末期指令较为平稳;最优制导律初期指令较小,但制导末段指令出现了较大幅度的波动。最优滑模制导律初期指令较小,在制导末期避免了指令波动的问题,表现出了良好的特性。

5 结 论

本文针对大落角目标逆轨拦截问题,首先建立了弹目相对运动模型,基于最优控制理论与滑模变结构控制理论分别设计了最优制导律与滑模制导律,随后将二者结合得到了最优滑模复合制导律,并采用扩张状态观测器对目标弹道倾角进行估计。之后,基于李雅普诺夫稳定性理论对最优滑模制导律进行分析,得到了参数的选取原则,并设计了过渡函数。最后,在目标有加速度机动和无加速度机动两种场景下,对本文设计的3种制导律进行数学仿真与对比分析。仿真结果表明,所设计的最优滑模复合制导律在两种场景下均能以期望的弹道倾角和较小的脱靶量命中目标,实现逆轨拦截,并且在制导过程中指令变化平稳,对目标的加速度机动具有较强的鲁棒性。