面向多无人机协同对地攻击的双层任务规划方法

余 婧, 雍恩米, 陈汉洋, 郝 东, 张显才

(1. 中国空气动力研究与发展中心计算空气动力研究所, 四川 绵阳 621000;2. 中国空气动力研究与发展中心空天技术研究所, 四川 绵阳 621000)

0 引 言

飞行器任务规划是随着航空技术和制导/控制技术的进步及其在军事上的应用而形成的一个新的研究领域。无人机(unmanned aerial vehicles, UAVs)的任务规划问题包含任务分配、执行顺序规划以及航迹规划等。任务分配是指确定哪些任务由哪些UAVs执行;执行顺序确定是指在已知任务集合的条件下,确定UAVs执行任务的先后顺序;航迹优化即确定UAVs执行任务的具体飞行航迹。任务分配与执行顺序规划都是典型的复杂约束下的组合优化问题,航迹规划的优化方式则因建模方式的不同而有所差别。一般而言,3个层次的优化问题相互嵌套、相互影响。执行顺序规划需要以任务分配方案为输入;航迹规划需要以任务执行顺序为输入;执行任务的航程或飞行时间又进一步影响任务分配方案的决策。为了达到任务规划的全局最优,需要全盘梳理3个层次的优化关系,提出高效的优化策略。

目前已存在多种UAVs任务规划的建模方法,包括旅行商模型、车辆路由模型、网络流模型、混合整数模型等,其中混合整数模型具有较强的可扩展性,车辆路由模型可以更好地处理带约束问题。针对优化模型,可以选择很多种搜索算法进行求解。传统的优化方法有枚举法、动态规划法、图搜索算法等,但随着问题维数的增加,时间消耗呈指数增长,不利于复杂问题的求解。随后,智能优化方法因具备易于实现、计算复杂度低等特点,被广泛应用。目前常用的智能优化算法有遗传算法(genetic algorithm, GA)、粒子群优化(particle swarm optimization, PSO)算法、模拟退火(simulated-annealing, SA)算法等。在当前研究中,任务分配与执行顺序规划因内在行为的紧耦合性,通常被作为一个整体考虑,因此任务规划问题大多侧重前两者的优化,而忽略航迹的影响。在优化算法方面,SA算法因在理论上有完备的证明,可以达到全局极小值,而备受研究者的青睐。在任务规划问题中,SA算法已有很多成功应用,但其亦存在一个致命的缺点,即容易陷入局部最优,因此研究者也一直在尝试诸多改进方法。

本文综合考虑任务规划中任务分配、执行顺序规划以及航迹规划3个层面的优化需求和相互间影响,从优化框架出发,设计了双层互耦的任务规划求解策略,而后将优化模型求解分为上层任务分配和下层任务序列优化,并对每一层的优化方法和优化步骤进行了详细设计;在任务分配问题中,基于SA算法,提出了可跳出局部最优的SA-撒点(SA-shooting, SAS)算法,并详细探讨了算法参数的设计原则。最后，通过仿真分析,验证了所提出的规划框架和优化算法的有效性。

1 任务描述

假设有无人攻击机架和待打击目标个,UAVs起飞后需要飞行至待打击目标位置进行对地攻击。一架UAV最多携带的武器数量为,即一架UAV最多攻击个目标，且一个目标只能被一架UAV攻击。任务分配的目的是优化出哪些UAVs需要打击哪些目标，以及实施打击的具体作战顺序、飞行路径,最大化对地攻击效益。图1给出了多UAV协同对地打击的示意图。

图1 多UAV协同对地打击示意图Fig.1 Sketch map for multi-cooperative UAV air-to-ground attack

2 多UAVs协同对地攻击任务分配建模

本文的UAVs对地攻击任务分配问题,可用四元组〈,,,〉来描述:

表示战场环境态势,包含了战场威胁分布、天气情况、地形等战场信息。为了方便讨论,本文将所有环境态势分为两部分,一部分为禁飞区,即由于雷达威胁、恶劣天气、不利地形所导致的UAV不可驶入的区域;另一部分即为UAV可以机动的区域。

即UAV状态,已知UAV集合={UAV,UAV,…,UAV},其中UAV={loc,},表示第架UAV的初始位置和所携带的武器数量,为UAV数量。

为待攻击目标集合={tar,tar,…,tar},为目标数量,且≤。

表示任务分配中的约束,包括任务时长约束、匹配约束、数量约束等,将在建模中详细讨论。

任务规划的本质是一个优化问题,包含设计变量、任务约束和评价指标3个关键因素。下面将对本文研究问题的关键要素进行分析和建模。

2.1 设计变量

(1)

2.2 评价指标

(1) 毁伤效果

假设UAV对tar的杀伤概率为 ,则整个攻击任务的毁伤效果为

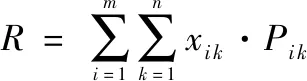
(2)

(2) 损伤程度

假设UAV对tar进行打击,生存概率为 ,则该UAV被击毁的概率为 =1- ,整个攻击任务的损耗可表示为

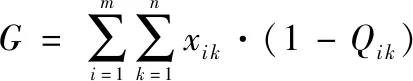
(3)

(3) 航程代价

UAV到达目标的航程越短,完成任务的时间代价就越小,航程代价需要在任务序列确定后,经过航迹规划给出,因此该评价指标仅在航迹规划时使用。令表示第架UAV的飞行距离,则整个任务的航路代价可表示为

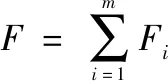
(4)

2.3 任务约束

在整个任务分配过程中,需要考虑以下任务约束:

:任务时长约束,UAV最长航行距离不得超过其航程限制。

:任务分配约束,每一架UAV都必须分配一个任务,每一个任务仅由一架UAV执行。

:禁飞区约束,UAV在航行过程中,不可经过禁飞区域。

:任务数量约束,第架UAV最多携带个武器。

:飞行姿态角约束,UAV进行机动时,有最大偏航角。

2.4 任务规划模型

综上,本文所研究的UAVs任务分配问题,可表示为如下优化模型:

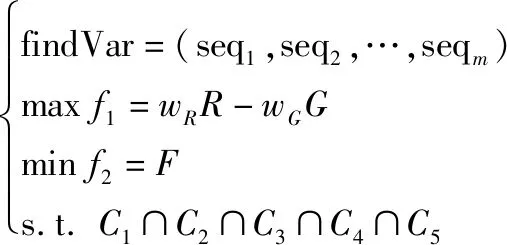
(5)

式中:和分别表示毁伤效果与损伤程度指标的权重系数,反映了二者的重要程度;可称为任务效益指标;为航路指标;至描述了需要满足的约束。

3 模型求解

3.1 求解框架

求解上述模型,理论上需要嵌套的两层规划去完成(见图2)。上层规划用于进行任务分配,即确定哪些UAVs执行哪些任务,主要满足优化指标;下层规划用于解决任务顺序和航路规划问题,即在已知UAVs需要打击的目标集合的前提下,优化出最优的任务序列和对应的飞行航路,主要关心优化指标。为了达到全局最优,上层规划和下层规划往往是相互联系和相互影响的,且在一定程度上,上层和下层的优化指标是相互矛盾的。当任务收益达到最大,可能航路代价并非最优;当选取了航路代价最优,则需要牺牲一些任务收益指标。

图2 双层任务规划框架Fig.2 Bi-level mission planning framework

本文认为,整个任务分配的效益指标远比航路指标重要。为提高规划效率,本文根据问题特点,对问题进行了简化,即上层规划仅考虑效益指标,下层规划仅考虑航路指标,规划策略如图3所示。

图3 双层任务规划策略Fig.3 Strategy for Bi-level mission planning

在下层航路优化中,根据已知的任务目标集合进行任务序列穷搜,而后采用已有蚁群算法,进行点对点航路规划,选取航路最优的任务序列为最终的任务执行方案,并给出对应的航路信息。

3.2 基于SAS的任务分配

任务分配为上层优化,任务分配的目的是优化出每一架UAV需要执行的具体任务的集合,而对具体的执行顺序和飞行航路不关心。任务分配模型,可以从公式中分解得出:

find= ,=1,2,…,;=1,2,…,

(6)

max=-

(7)

(8)

(9)

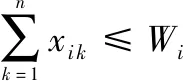
(10)

(11)

式(6)表示任务分配的决策变量,式(7)表示任务效益指标,式(8)表示每个目标只能被分配给一架UAV,式(9)表示每架UAV都必须被分配目标,式(10)表示UAV具有多目标攻击能力,最大攻击数取决于自身携带的武器数量,式(11)表示所有目标都必须被分配给UAVs。

任务分配是一个典型的组合优化问题,SA算法是其求解方法之一。SA算法是一种通用的随机搜索算法,是对局部搜索算法的扩展。与一般局部搜索算法不同,SA以一定的概率选择邻域中目标值相对较小的状态,是一种理论上的全局最优算法。在实际应用中,SA算法易于陷入局部最优,因此需要根据具体问题进行有针对性的改进,以跳出局部最优。

本文主要用SA算法进行任务分配优化,并在基本算法基础上拓展撒点算子,以跳出局部最优,下面对其关键步骤进行介绍。

(1) 编码设计

如果直接以决策变量编码,则是一个×维的矩阵,比较浪费空间,且不利于寻优搜索。为了便于邻域搜索,本文的编码设计为1×维的向量,为待打击目标的数量。假如向量中第个元素的值为,则表示 =1。假如求解的规划问题有5个任务,则一个状态编码如图4所示。

图4 状态编码示例Fig.4 Example for encoding

图4中的编码表示,任务1分配给UAV,任务2分配给UAV,任务3分配给UAV,任务4分配给UAV,任务5分配给UAV。

(2) 邻域搜索

算法的编码为整数编码,且编码需要满足模型中的各种约束。在领域搜索的过程中,采取概率赋值的方式。具体方法如下(见图5)。

图5 邻域搜索示例Fig.5 Neighborhood searching

随机选取编码中的个位置;

依次将个位置上的值,随机赋予一个不同的值,赋值范围为1～。

(3) 撒点算子设计

SA算法的缺点是易于陷入局部最优,因此在迭代的过程中,本文引入撒点算子,其基本原理是,在整个搜索空间随机选取若干候选编码,通过目标函数值计算,选取最优编码为邻域编码。在传统的SA算法中,仅根据当前编码选取一个邻域解作为候选点,不仅搜索空间有限,而且候选点数量很少。加入撒点算法后,首先邻域搜索范围扩展到了整个寻优空间,不局限于邻域,即跳出了邻域局部空间的束缚,其次撒点操作一次性并行地搜索多个候选点,有利于提高搜索效率,尽快找到更优的候选点。通过随机撒点,可以尽快跳出局部最优,提高传统算法的全局寻优能力。具体步骤如下:

判断优化过程是否满足无条件转移,如果满足,继续下一步;

随机生成pop个编码(pop称为撒点算子规模);

对编码进行目标函数值计算,选取目标值最优的编码为邻域编码,并赋值给当前编码。

(4) 算法流程

SAS算法的具体流程如图6所示。

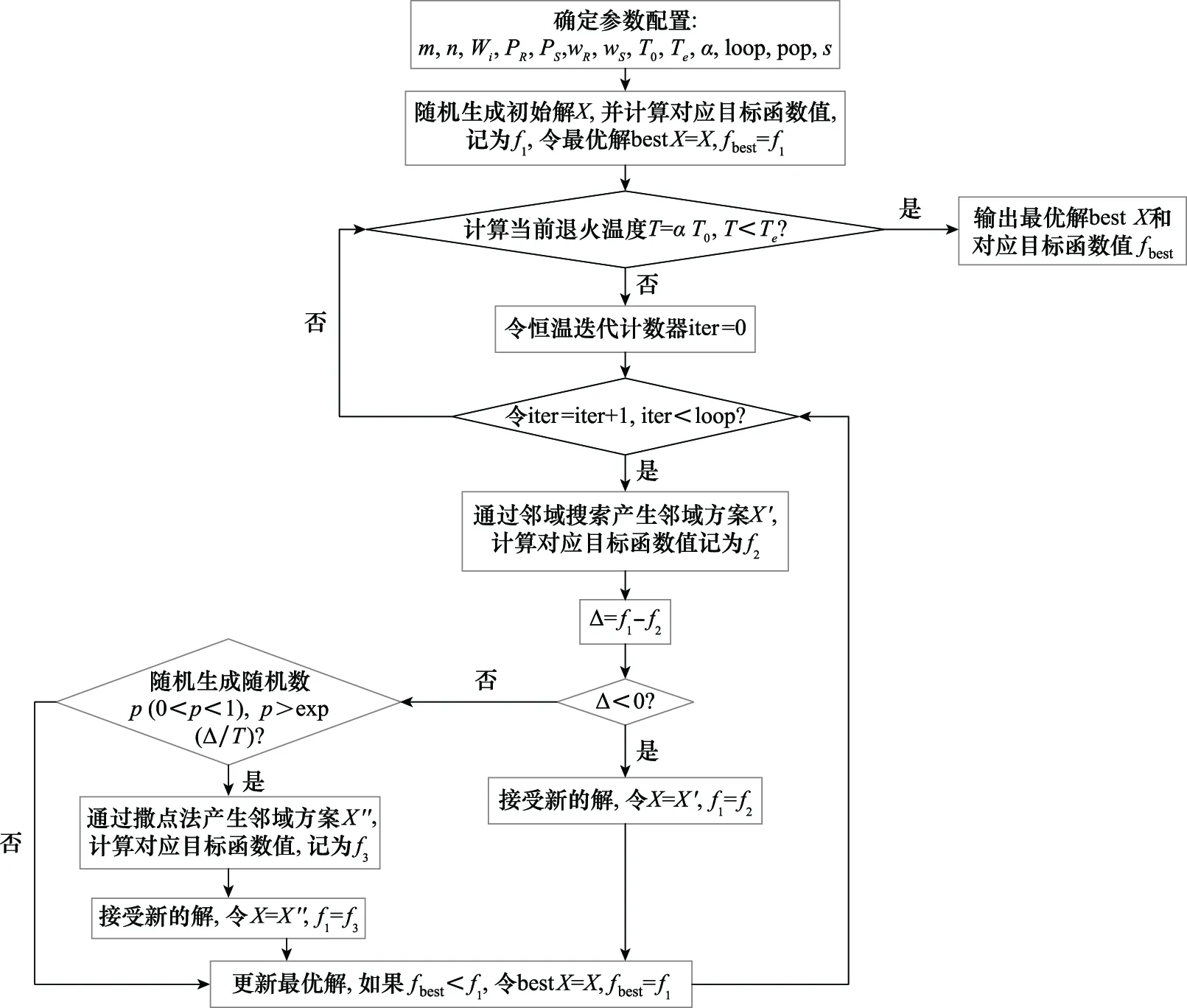
图6 SAS算法流程Fig.6 Flowchart for SAS

(5) 算法复杂度分析

与传统的SA算法相比，本文所改进的SAS算法，主要是在邻域搜索结束后，多了一个撒点算子操作，撒点操作过程中，需要进行目标函数值计算，且计算过程是并行的。假设计算一次目标函数的计算代价为，时间代价为，记传统SA算法的计算代价为SA ()，时间代价为SA ()，则可推知，从时间上看，本文改进的SAS算法的时间代价为SA ()+iter·，即每一次迭代仅比传统算法多了一个时间单位的代价。这是由于，尽管撒点算子过程中进行了多次目标函数值计算，但计算过程是并行的，总时间消耗仅多出一次目标函数值的计算时间。从计算复杂度上看，改进算法的计算代价为SA ()+iter·pop·，比传统算法略高，且复杂度与撒点算子规模有关。

3.3 任务序列优化

当每个UAV的攻击任务集合已知,则可进行下层优化,即任务序列优化。任务序列优化的目的是规划出UAVs执行任务的顺序以及对应的航路。下层优化的模型,可表述为

(12)

min=

(13)

s.t.∩∩

(14)

本文采用已有的蚁群算法进行航路规划,蚁群算法在此不再赘述。下层优化的具体步骤如下:

针对第架UAV,根据已知的任务集合,穷搜可能的排序组合;

针对每一组任务序列组合,调用已有的蚁群算法,进行航路规划,并记录最优航路代价;

选取所有排序组合中航路代价最优的组合,作为最优任务序列输出,并同时输出飞行航迹。

4 仿真分析

本文的仿真不考虑UAV间的通信与在线协同问题，战场环境威胁均简化为数学模型，且假设UAV飞行为匀速飞行，不考虑飞行高度等因素。

4.1 任务分配仿真

(1) 算例配置

假设UAVs数量=6,任务目标数量=10,每架UAV携带的最大武器数量为=4(=1,2,…,),UAVs的毁伤概率和生存概率随机给出,具体数值如表1和表2所示。定义==05。SA算法的参数值由表3给出。

表1 毁伤概率Table 1 Destructive probability

表2 生存概率Table 2 Survival probability

表3 SA算法参数设置Table 3 Parameter configuration for SA algorithm

(2) 优化参数影响分析

假设撒点算子规模始终为50,改变邻域搜索过程中元素位置搜索数目,连续运行5次优化程序,其优化结果如表4所示。

表4 邻域搜索参数对优化结果的影响Table 4 Optimization results with different neighborhood searching parameters

从表4可以看出,不论参数设置为1还是10,算法的搜索结果都相对稳定,总体上趋于较好的优化结果,且优化结果的方差不大。从表4还可看出,邻域搜索的位置数目并不是越多越好,当搜索数目为1和3时,都能够得到最优解4.025,当搜索数目变大时,虽然也能得到较好的优化结果,但不容易得到相对最优的结果。这是由于随着搜索数目的增大,邻域搜索空间也增大,在有限的搜索次数内,并不能保证搜到邻域的最优值。从表4可以推断出,当编码有10个值时,邻域搜索位置数目设置在3比较合适。

根据表4结果,将邻域搜索位置数目设为3,改变撒点算子规模,连续运行5次优化程序,优化结果如表5所示。

表5 撒点算子规模对优化结果的影响Table 5 Optimization results with different shooting populations

撒点算子的设计,是为了解决SA算法容易陷入局部最优的问题。从表5可以看出,随着撒点算子规模的增加,算法的寻优效果越来越好。这是由于撒点算子规模越大,搜索的空间越大,则跳出局部最优的概率越大。

图7和图8给出了表4和表5优化中最优结果的收敛过程。

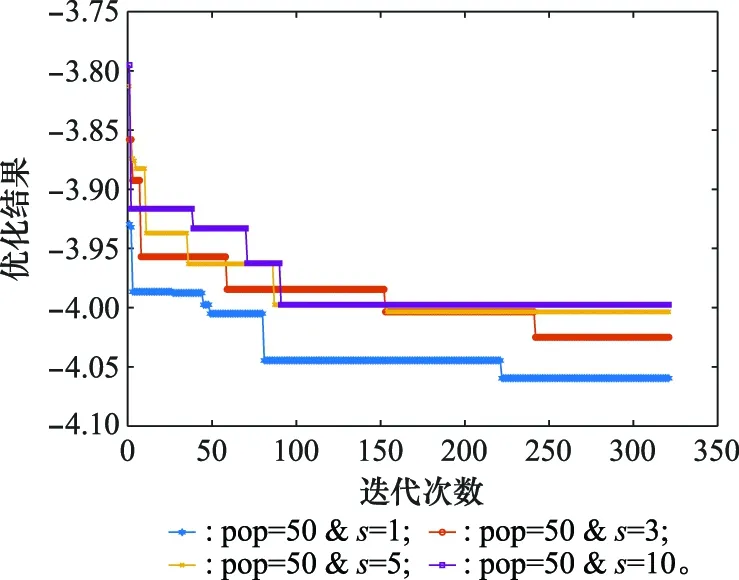
图7 邻域搜索参数变化的收敛过程Fig.7 Convergence process with different neighborhood searching parameters

图8 撒点算子规模变化的收敛过程Fig.8 Convergence process with different shooting populations

(3) 算法对比分析

图9给出了本文的SA算法与传统SA算法以及PSO算法的收敛对比。从图9可以看出,本文提出的SAS算法收敛效果最好,传统SA算法次之,传统PSO算法最差。PSO算法更善于处理连续优化问题,传统编码对组合优化问题的适应性不强,且迭代次数较少,导致其优化效果较差。SAS算法由于设计了跳出局部最优的撒点算子操作,优化效果优于传统SA算法。

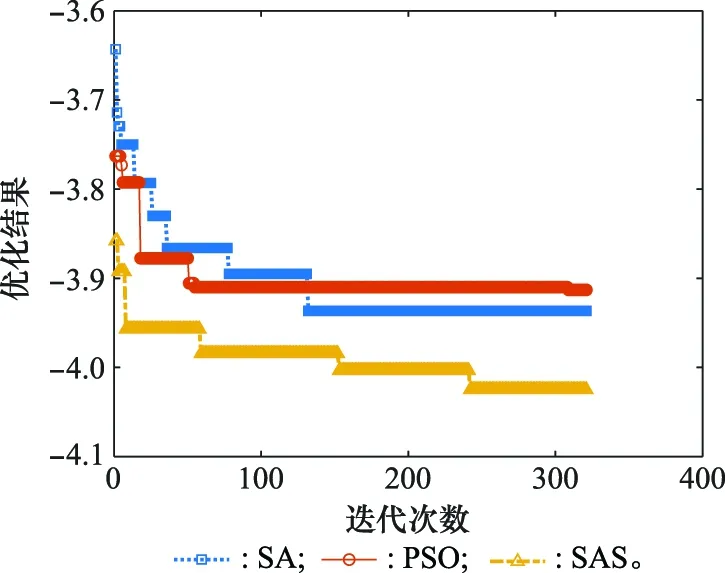
图9 不同优化算法的收敛过程对比Fig.9 Convergence process for different algorithms

(4) 优化结果与分析

从表4和表5中选取最优的一组优化结果,其任务分配情况如表6所示。

表6 最优分配结果Table 6 Optimal results for assignment

从表6中可以看出,优化的结果均满足公式约束。任务大多趋于分配给UAV,这是由于在随机给出的毁伤概率和生存概率中,UAV的数值都比较好。UAV的概率数值都较差,如果没有任务数量约束,整个任务分配偏于将任务分配给其他UAVs,而非UAV。

4.2 任务序列优化仿真

本节根据表6的任务分配结果,进行任务序列优化。

(1) 算例配置

在任务序列规划中,涉及到航迹的规划,需要给出飞行环境。本算例中,飞行环境主要考虑无人机、目标的位置、飞行区域以及涉及到的环境、雷达和导弹威胁。任务目标的地理位置如表7所示,各威胁的编号、类型与坐标如表8所示。整个任务的执行区域限制在[0, 0] km到[60, 60] km范围内。为了进行航迹规划,需要对飞行区域进行地图数字化,本文采用栅格法进行地图建模,栅格离散化间隔为2 km。无人机初始位置为[2, 2] km。

表7 任务目标坐标Table 7 Coordinates for targets

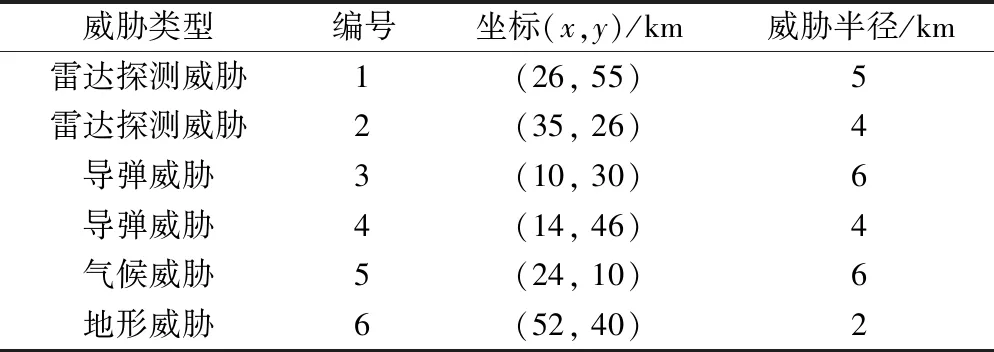
表8 威胁分布Table 8 Distribution for threats

(2) 任务序列枚举

从表6可知每架无人机的目标任务集合。第3.3节已给出了任务序列规划的具体方法,首先需要对任务集合中的所有序列组合进行枚举。如表9所示,UAV～UAV都只有一个目标任务,因此可能的任务序列组合只有一种。UAV有24种可能的组合方法,而UAV有2种。每一种可能的任务序列组合都将采用蚁群算法对其进行航迹规划,记录航程,其中航程最短的组合将最终被定为UAV需要执行的任务序列方案和飞行航迹方案。

表9 任务序列枚举Table 9 Enumeration results for mission sequences

由于UAV～UAV只有一个任务目标,采用航迹规划算法进行点对点航迹规划即可,具体优化结果如图10所示。UAV有两个任务需要执行,可能的任务序列为[2, 7]和[7, 2]。当任务序列为[2, 7]时,最优飞行航迹如图11所示,航程为68.08 km。当任务序列为[7, 2]时,最优飞行航迹如图12所示,航程为87.94 km。因此,UAV的最佳任务序列为[2, 7]。UAV有24种可能的序列组合,经过优化,其最优任务序列为[1, 9, 3, 8],飞行航迹如图13所示,航程为149.05 km。

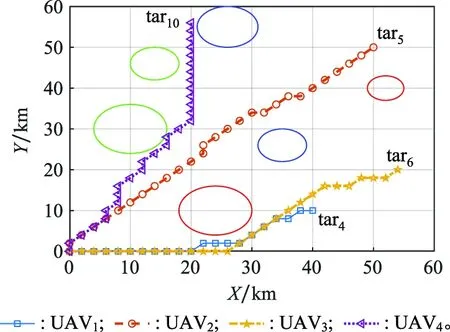
图10 UAV1～UAV4飞行航迹Fig.10 Trajectories for UAV1～UAV4

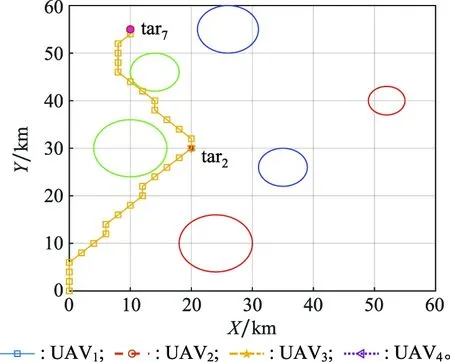
图11 UAV6执行任务序列[2, 7]的飞行航迹Fig.11 Trajectory for UAV6 attacking targets [2, 7]

图12 UAV6执行任务序列[7, 2]的飞行航迹Fig.12 Trajectory for UAV6 attacking targets [7, 2]

图13 UAV5飞行航迹Fig.13 Trajectory for UAV5

5 结束语

UAVs的任务规划包含任务分配、执行顺序确定以及航迹优化等。为了达到任务规划的全局最优,需要全盘梳理任务的各个方面,提出高效的优化策略。本文综合考虑任务规划过程中任务分配、执行顺序确定以及航迹优化等方面的需求和相互间影响,首先从优化框架出发,设计了双层互耦的任务规划求解策略,而后将任务规划模型分为上层任务分配和下层任务序列优化,并对每一层的优化方法和优化步骤进行了详细设计;在任务分配问题中,基于SA算法,提出了可跳出局部最优的SAS算法,并详细探讨了算法参数的设计原则。通过仿真分析可知:① 本文提出的双层规划策略,可有效梳理3个层次的优化关系,利于优化求解。但需要注意的是,双层规划策略的应用以任务收益优先为前提,当航程等指标优先级较高时,需要对规划策略进行进一步改进。② 本文提出的SAS算法可以跳出局部最优,有效进行任务分配优化。在算法参数设置过程中,邻域搜索时的可变位置数目并不是越多越好,一般设置在编码总数的1/3左右;而撒点算子规模的设置则是越大越好,规模越大,搜索的空间越大,则跳出局部最优的概率越大。

在进一步研究中，将更多考虑实际应用场景，考虑UAV间的协同、通信、复杂电磁环境、飞行高度等问题。