储供基地支援保障能力评估混合算法

周文明, 崔德康, 周婧怡, 张明明, 朱安石

(1. 国防大学联合勤务学院, 北京 100858; 2. 桂林电子科技大学人工智能学院, 广西 桂林 541200; 3. 中国人民解放军32707部队, 北京 100071)

0 引 言

联勤储供基地是联合作战联勤支援保障的重要力量,是实施机动支援保障的重要依托,也是抽组机动支援保障力量的重要来源。战时对储供基地保障能力进行有效评估和物资仓储供应优化决策,是科学运用储供基地力量和资源进行战役支援保障的前提和基础,是保障决策辅助的重要且科学的有效手段,对提高储供基地物资供应保障军事经济效益具有重要价值。

从研究资料看,在仓储供应保障能力评估方面研究并不多,唐梦妮等对仓库管理保障能力指标体系构建原则和构建方法方面进行了研究,但没给出保障能力评估方法。谢鑫鹏等只对车辆器材仓库收发单项能力评估进行了研究。梁展对军用车辆装备维修器材仓储管理从理论上及研究现状等方面进行了研究,提出车辆装备维修器材库存管理诸多优化措施,但没有进行联合作战支援保障能力评估方法、保障辅助决策等相关内容的研究。王嫣等运用层次分析法对仓库航材保障能力评估进行了研究,考虑了战时、业务、建设等多个方面,但研究内容较为泛化,针对性不强。文献[6-16]主要从理论上研究了储供基地、军种保障基地等单位的建设设想、思路、措施等方面提出自己的观点,没有从保障能力评估的角度提出相应工程化方法,因此为战时支援保障辅助决策提供决策支持的适用性不强,为平时能力建设提供借鉴参考的说服力也明显不足。

综上所术,目前大部分研究都是将仓储和供应分开研究,研究的物资种类比较单一,评估和辅助决策算法也比较单一,而储供基地往往是储备许多类后勤和装备物资器材,储、收发装卸、运输供应等工具手段也不尽相同,人员技术同样有所差别,因此单一的评估算法和优化方法很难准确、合理、有效地对其进行能力评估和辅助指挥决策。本文将储供基地实体部(分)队整体作为研究对象,对其联合作战支援保障能力进行综合考察,对其仓储、装卸供应和部分投送能力一体化考虑,提出一种混合算法,即综合运用多种算法,针对不同指标的量化分析需求,采取有针对性地量化方法计算其指标值,最后通过指数综合方法计算出储供基地的综合保障能力,为战时遂行支援保障指挥决策,提高其保障效能提供技术支持。

1 仓储供应保障要素分析

根据赋予储供基地的职能任务,以及其勤务支援保障流程,其勤务保障环节主要涵盖物资的筹措、接收、储备、装卸供应、少量的物资投送等,也是分析保障能力影响因素的依据。此外,信息化水平是未来信息化作战仓储供应保障能力的重要影响因素,起到能力倍增器的作用。鉴于战争总是有先兆,预有准备,因此在评估储供基地支援保障能力时,只考虑储存内容、储存数量、装载能力和效率、有限投送物资能力等相关的能力影响因素。当然,指挥控制能力、防卫能力、人员素质等都对勤务支援保障产生影响。综上所述,在借鉴可拓学中的发散-相关方法下,建立了储供基地勤务支援保障能力评估指标体系,并通过运用信息论中的背景压缩、相似压缩、奇点压缩方法对其进行约简,建立如图1所示的评估指标体系。

图1 储供基地勤务支援保障能力指标体系Fig.1 Service support capability index system of storage and supply base

2 指标的量化

根据建立的指标体系,分别采用考核评价、专家经验法、定义量化法、层次分析法、排队网络法、模糊综合、指数综合等算法来量化各指标的值。

2.1 定义量化方法

装备满编完好率,用所配备的保障装备中新、堪数量占比数表征，反映了装备配备完好的总体保障能力水平,用表示如下：

(1)

式中：为配备保障装备中新、堪数；为保障装备的编制数量。

设施配套完好率,是指保障设施配套且新、堪占比率,反映了保障设施保障水平,用表示如下:

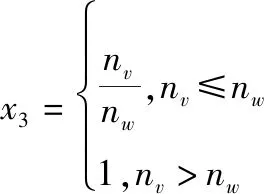
(2)

式中:为配备设施中新、堪设施的数;为设施应编数。

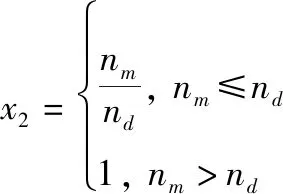
保障物资储备水平,是指保障物资,如油料、弹药等物资的实际储备数量与战时可能需要保障的数量之比,反映了各类物资战时储备保障水平,即战时对各类作战物资需求的满足程度,用表示如下：

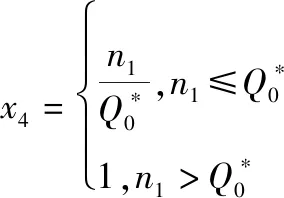
(3)

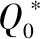
装卸载能力,就是物资供应保障中的装载和卸掉物资能力,通常用在指定的时长内完成装载交通工具的数量除以排队等候交通工具的总和来表征,用表示如下:

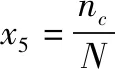
(4)

式中:表示已完成装载的的交通工具数,其计算方法见第4节;表示排队等候的交通工具总量。

物资装载和卸载是储供基地物资供应保障中的重要环节,装载部(分)队的职责就是在指定的时长内,最大限度地完成交通运输工具的装配任务,确保各类物资满足战场需求。

2.2 军事运筹量化方法

战时运输投送虽然不是储供基地最重要的任务,但根据新的储供基地的职能任务要求,战时还应承担部分的运输投送任务,主要是储供基地所能辐射范围内的近程投送任务。物资运输投送问题比较复杂,目前对于储供基地来讲,因不具备空运、海运、以及铁路运输能力,所以主要考虑公路运输方式。影响运输投送能力的因素很多,难以用数学解析方法计算,针对公路运输投送,假设运投能力用表示,车况(含维修),路况,编配组织,防卫,路程，(=1,2,3,4,5)的取值由专业人员计算,则的值计算如下:

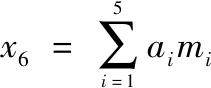
(5)

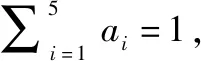
人员在仓储供应保障过程中始终起着决定性作用,用表示人员的素质和能力。人员包括指挥人员、信息保障人员、警勤防卫人员、物资管理人员、装卸人员等类别。分类综合考虑各类人员的学历专业、文化科学知识和军事科学知识学习情况、岗位受训情况等构成的知识结构;包括创新、学习、自我管理等在内的能力构成;包括身心健康、政治、军政在内的素质结构进行打分评价。总体来说,人员因素是一个模糊因子,这里选择以模糊综合的方法得到人员能力指标的量化评估值。

信息化联合作战中的信息保障能力是影响保障效能的重要因素,用表示。主要包括情报、保障需求、保障命令指示等信息的获取和传输;需求信息和保障任务信息的处理优化,以及信息对抗中的信息保密、抗干扰等内容。信息保障能力中的诸多指标很难确定哪个更重要,因此也是一个模糊类因子,其量化方法可通过专家评估后采用模糊综合的方法得到综合量化分值。

2.3 实际考核评价量化方法

指挥控制能力主要考察指挥组织机构设置、综合判断能力、协调能力、机关工作效率、决心方案设计论证的质量等,用表示。防卫能力主要包括防发现(即伪装)能力、地面警勤防破坏能力等,用表示。和的量化主要采取实际考核方法确定。

3 战时物资保障需求计算

战时物资保障需求计算是量化储供基地保障物资储备水平指标的必要步骤,也是最优化保障物资储备数量的重要参考。战时储供基地各类保障物资到底应该储多少,才能满足保障需求,并实现最大军事经济效益,这是储供基地面对的基本问题。

3.1 基本假设与问题提出

假设每供应一个单位某类物资(如1 t油料、弹药、军需物资等)所产生的军事经济价值为sx元。军事价值随某次战役价值而随机变化,通常军事价值比较大,如影响战争进程和战争胜负,所以常取比较大的值更为合理。当然也可以换一种角度来说,设定因产生的军事价值而获得激励性奖励sx元,当然奖励金额是次要的,为赢得战争所提供的保障支持是主要的,通常sx取较大的值。如果因供过于求,则剩余库存物资每个单位需付出库存维持成本费用sy元。根据战争经验,不同规模和烈度(强度)战争中该类物资需求数量的概率(记作())是已知的,那么需要计算出该储供基地一次该规模和某烈度作战最佳储备该种物资的单位个数(可设为)。

3.2 建模与求解

从损失期望最小的角度建模求解，设某次联合作战规模和强度已知,此次作战该类保障物资需求量是离散随机变量,其概率(已知)服从泊松分布,即

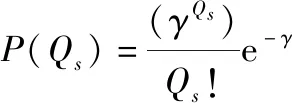
(6)

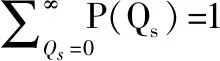
设储供基地储备该物资的数量为,则:① 当供过于求时(≤),仓库因积压而承担的仓储维持成本损失的期望为

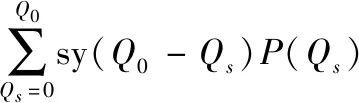
(7)

② 当供不能满足作战供应需要时(>),因缺货而对作战进程和胜负造成影响通常考虑为较大,这里以较大的军事价值成本损失来近似代替,即每单位成本损失为sx元。则成本损失期望为

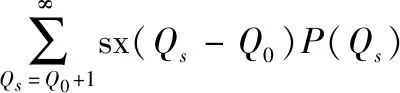
(8)

综合以上两种情况,可得储供基地储备该类物资量为时，成本损失的期望值()为

(9)

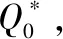
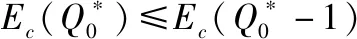
(10)

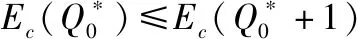
(11)

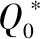
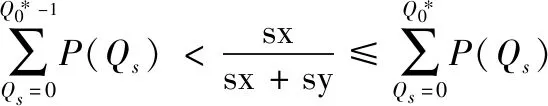
(12)

4 确定装载完成运输工具的数量

确定装载和卸载的值,首先需计算在指定时长内完成装车量的值,这里用排队论中的排队网络模型计算和的值。

根据排队网络相关理论,分以下两种情况分别计算。

单个待装载交通工具仅装一种物资(如:军需物资、战救药材、弹药或器材)

模型假设:

(1) 运输保障物资交通运输工具的到达时间差服从负指数分布,参数为,表达式如下:

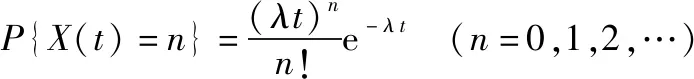
(13)

(2) 运输交通工具到达多个点位。

(3) 待保障物资共分种。

(4) 在时刻同时有个交通工具抵达,每辆交通工具仅运送一种物资类别。

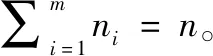
(6) 每个排队按先到达先服务原则。

(7) 每个点位中的队列又分多个装运点,也称服务台,其多少分别为(=1,2,…,),=为各个点的利用参数因子,用来衡量忙碌的时间均值,即排队的装运能力(sμ)被待装交通工具()利用的水平,为排除无限队长,取<1。

由假设可见,各个站点都是一个独立的系统,全部站点构成开放的排队网络,因单个运输交通工具仅装运一类物资,所以仅需通过一个服务台,计算比较简单。按照状态的统计平衡情形要求,排队网络的稳态方程如下:

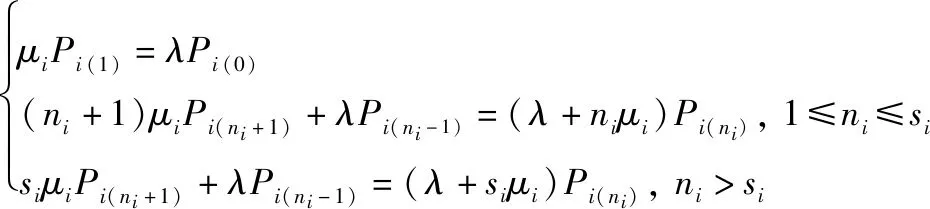
(14)

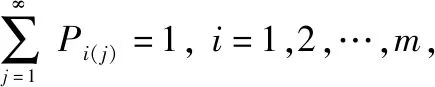
用递推法解上述差分方程,可求得状态概率为

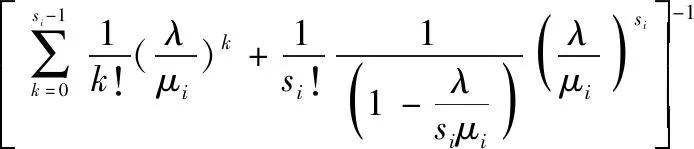
(15)

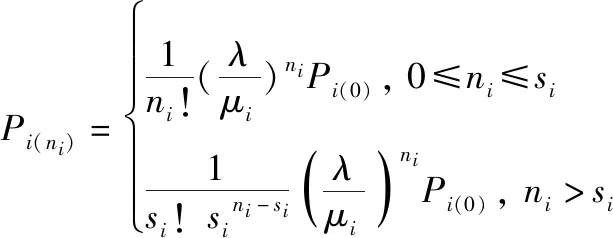
(16)

期望(平均)队长和期望(平均)等待队长分别为

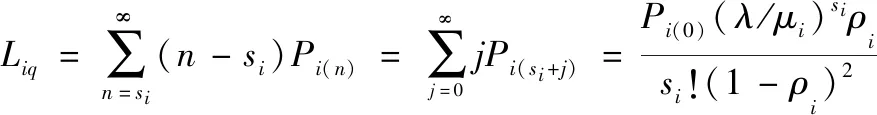
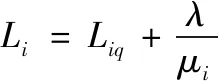
(17)

每辆交通运输工具期望(平均)等待时长和期望(平均)停留时长由Little公式求得

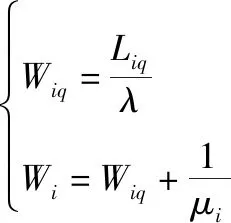
(18)

解得停留时长后,便可获得时长内平均装运完成的交通工具数量:

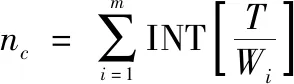
(19)

式中：INT[·]表示取整。由此可计算获得装运分队的任务完成能力:

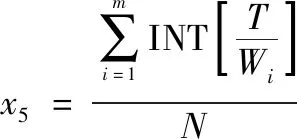
(20)

单个交通运输工具同时装运多类物资

在战时交通运输工具经常一次运送多类物资(如军需物资、战救药材、弹药等),待装运交通运输工具需通过不同物资装运地点,即需要通过两个以上装运设施。

模型假设:

(1) 若时刻有台交通运输工具排队,单个运输工具均要装运物资(≥2)类。

(2) 若一装运工具在装运站点完成装运后,以概率, 到达装运站点。

(3) 设排队空间无限，则所有排队组成一个开放排队网络。

一台运送工具离开设施以概率, 到达下一装运站点(=1,2,…,),或者以概率离开装运系统：

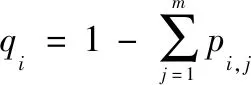
(21)

记(=1,2,…,)为第个装运排队总到达率,即可按该排队外的到达率与别的装运站点转来的到达率相加计算获得

(22)

令=,=1,2,…,,称(=1,2,…,)为第个装运站点服务因子。若所有满足<1,则称网络为平稳的。记服务站点前面的待装运交通运输工具排队长为,可得装运站点网络的平稳排队长分布概率为

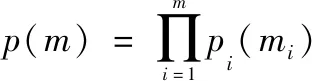
(23)

其中:

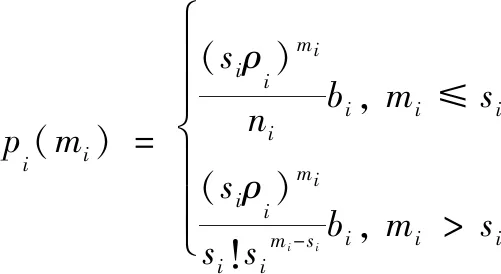
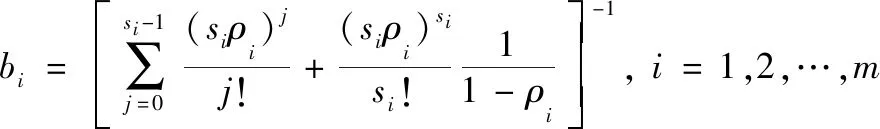
同情况1,分别求解获得每个装运排队的平均等待时长和停留时长。

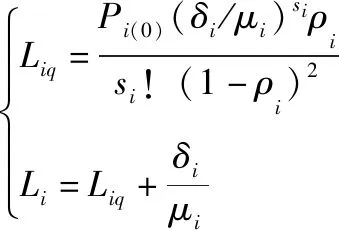
(24)

式中:参数由求解式(24)获得,设为系统的到达率,是所有从其他装运站点来到该装运点的到达率，=,则

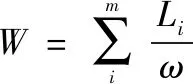
(25)

在时长内平均完成装运的交通运输工具数,装运部(分)队的装运保障能力的计算分别如下:

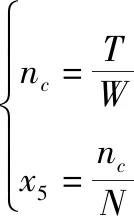
(26)

5 指数综合模型

指数综合法具有较好的综合评估分析特点,能很好体现指标间的关联关系。基于指数综合法的视角考虑,储供基地支援保障能力与各指标之间存在着一定关联(数量)关系,用函数表示如下:

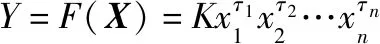
(27)

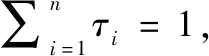
基地勤务支援能力的9个指标中,同耦合紧密,但、、、、和对总体的影响具有间接性,与其他指标相关性不强。故选用～作为指数, 将用作调节项因子。运用上文各项指标的计算方法确定各项指标的数值,得到指数模型如下:

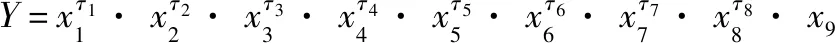
(28)

其中,(=1,2,…,)由层次分析法给出。

6 实例分析

设某储供基地储备物资种类包括军需物资、维修器材、战救药材、油料和部分通用弹药,物资储备水平由式(6)～式(12)计算。根据物资类别,装卸服务设施分为6类,每一类服务设施中设置装卸若干站点,即服务台若干,根据排队情况和装卸设备数量开设。6类装卸服务设施的装卸站点数量和服务效率基本数据如表1所示。其中，装运时长均以小时计量,单位时间(如1 h)装完某类物资运输工具数量定义为服务率(即)。假设某次小规模低强度联合作战时,支援保障运输车辆到达服从=0417的泊松分布,每一类运输车辆只负责运送一类物资(运送多类物资情况类似求解)。设装备满编完好率为093,设施配套完好率为096,保障人员综合能力为098,投送能力为086,指挥控制能力为087,信息保障能力为076,防卫能力的值为088,保障物资储备水平为0997。

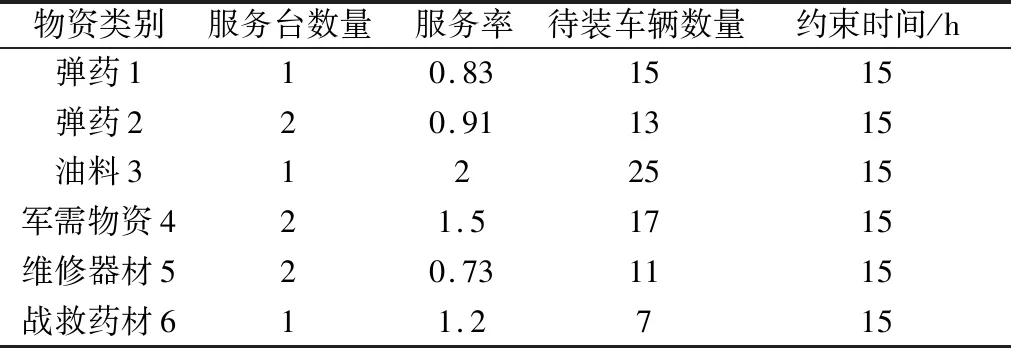
表1 小规模低强度储供基地物资装卸分队基本情况Table 1 Basic information of material loading and unloading unit of small-scale and low-intensity storage and supply base

根据式(15)～式(20)计算,即平均队长、等待队长、停留时长、等待时长、完成装运交通工具数和物资装载效能,计算值如表2所示。“装载完成数量”表示为(),表示在给定的时间里可以装载完成车辆数,表示实际装载车辆数。

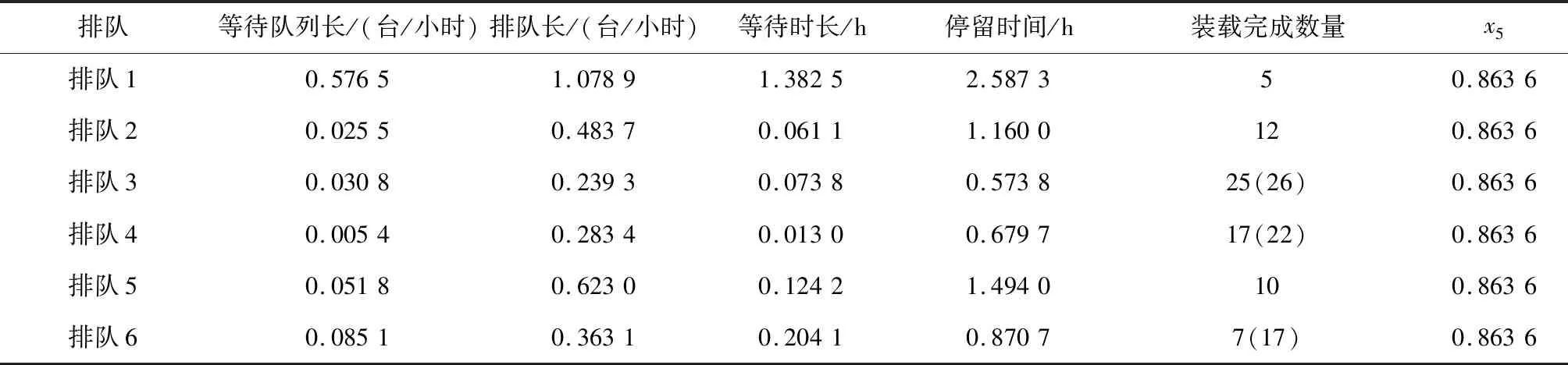
表2 小规模低强度储供基地支援保障物资装卸保障结果Table 2 Loading and unloading support results of support materials for small-scale and low-intensity storage and supply base

结果分析:通过层次分析法确定出=0133,=0099,=0097,=0188,=0145,=0126,=0105,=0107。

运用式(28)即可求得储供基地保障能力:

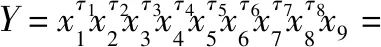
从表2可以看出,排队1、2、5在规定的时间内没能按规定时间装完待装的运输工具,主要原因一是几个排队的工作效率较低;另一个原因是各排队的服务台数量仍不能满足装载任务要求,尤其对于某些弹药和维修器材装载难度可能稍大,服务率较低。

6.1 相同规模强度下保障能力评估计算

在同等作战规模和强度(即小规模低强度联合作战条件不变)下,如何提高储供基地的支援保障能力,这是勤务保障指挥人员根据评估结果进行思考辅助决策的问题。可以根据具体的装载对象和时间要求,通过提高人员操作技能,或者提高装载专用设备配备来提高服务率;也可通过增设服务台,即增设装载点来提高保障效率。例如,通过提高弹药1排队装载人员的操作技能和增加专用装载设备来提高服务率达098,并增加一个服务台,使其在规定的15 h内保障能力达到装载完成14辆,整体装载能力从0864提高到0966,如表3和表4所示。同时提高信息化水平到097,则储供基地的整体保障能力为

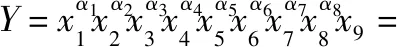
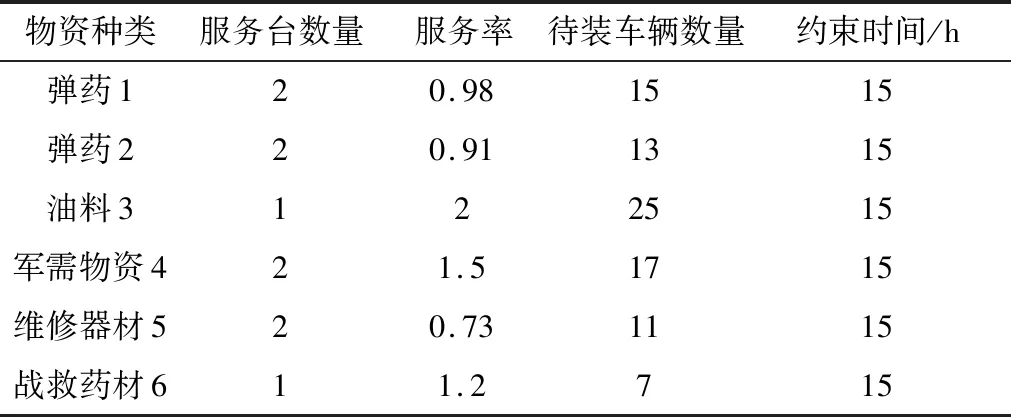
表3 小规模低强度储供基地物资装卸分队情况Table 3 Material loading and unloading team of small-scale and low-intensity storage and supply base

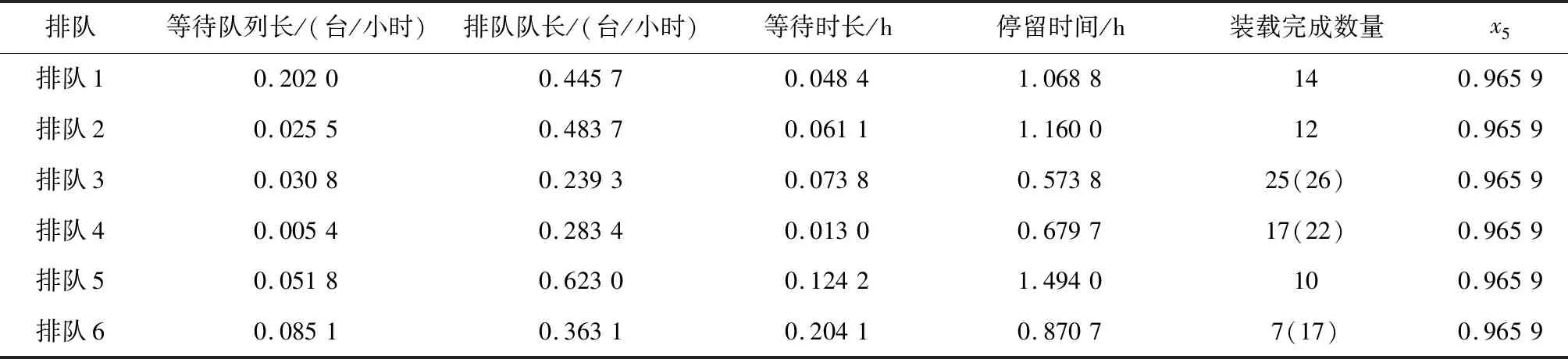
表4 小规模低强度储供基地支援保障物资装卸保障情况Table 4 Loading and unloading support of support materials for small-scale and low-intensity storage and supply base

在相同作战规模和强度条件下,通过提高装卸载能力和信息化水平使得储供基地的整体保障能力从0.791 2提高到0.893 2,如图2所示,从而有效提高了储供基地的综合保障能力。

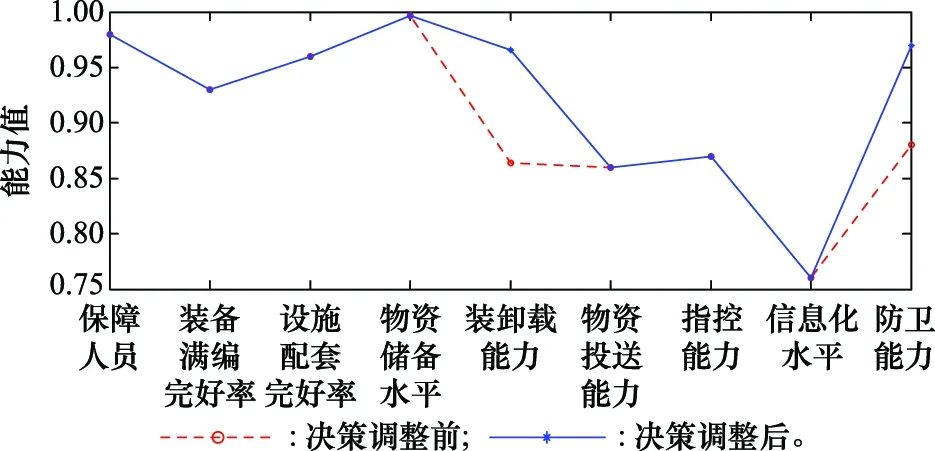
图2 小规模低强度作战条件下提高单项指标保障能力前后能力值对比图Fig.2 Comparison of capabilify before and after improving the support ability of single index under the condition of small-scale and low-intensity operation

6.2 不同规模强度下的保障能力评估计算

当作战规模和强度提高,则保障强度显然必然要随之提高,仓储水平、装卸载能力、运输投送能力、信息化水平及其他指标显然要求更高。

假设某次作战规模调整为中等规模,强度提升为中等强度,此时支援保障运输车辆到达服从λ=0.497的泊松分布,支援保障物资同上,若服务台和服务率保持不变,但待装载车辆的数量必然增多,具体情况如表5所示,此时装卸载能力计算如表6所示。

表5 中等规模中强度储供基地物资装卸保障分队情况Table 5 Material loading and unloading support unit of medium scale and medium strength storage and supply base

表6 中等规模中强度储供基地支援保障物资装卸保障结果Table 6 Loading and unloading support results of support materials of medium scale and medium intensity storage and supply base

可见,除了排队4,其他排队的物资装载都不能完成预期任务,由此装卸载能力降低到0.578 5。同样,其他指标的值同样因为作战保障强度的提高,其装备损坏率都相应提高而下降,保障人员的技能也会因作战强度的提高而降低,由于篇幅限制,这里只给出计算结果如下:=0977,=089,=091,=093,=0578,=083,=086,=075,=087。

此时,储供基地的保障能力为

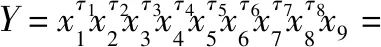
09770133×0890099×0910097×0930188×05780145×

0830126×0860105×0750107×087=0721 6

可见,在中等规模中等强度联合作战条件下该储供基地的保障能力远不能满足保障需求,当前能力至多算是及格水平。为了保证能够满足在中等规模和中等强度作战条件下的支援保障能力要求,平时必须加强各类保障人员的理论培训和技能训练,战时必须相应增加各类物资的服务台数量,装卸装备和设备的性能,并提高服务率,同时提高物资的储备水平、信息化保障水平、运输投送能力,相应加强防卫能力,这样才能满足较高规模和强度联合作战储供基地的支援保障要求。

7 结 论

本文建立的储供基地支援保障能力评估混合算法,能有效评估储供基地综合保障能力,该算法模型也为储供基地的物资储备水平、装卸载、人员的调整和培训、信息化建设、投送能力的提高等诸多方面提供决策依据和方法。