基于稀疏表示分类的雷达欺骗干扰识别方法

周红平, 马明辉, 吴若无, 许 雄, 郭忠义

(1. 合肥工业大学计算机与信息学院, 安徽 合肥 230009;2. 电子信息系统复杂电磁环境效应国家重点实验室, 河南 洛阳 471003)

0 引 言

雷达作为现代战场上一种全天候信息传感设备,无疑成为了战场态势感知、侦查监视、武器制导以及目标识别等方面的核心设备。正是由于雷达在战场上发挥着重要的作用,往往会成为现代战争中首先被打击的对象。数字射频存储(digital radio frequency memories,DRFM)干扰机可以快速地捕获雷达发射信号,其内部有高频率的采样设备,可以高保真地恢复雷达发射信号并进行调制,产生具有欺骗性质的干扰信号,由于欺骗干扰信号和雷达回波信号高度相干,进入雷达接收机时与雷达回波信号获得相同的脉压增益,使得雷达无法辨别真假信号,因此欺骗干扰现已成为雷达的主要威胁。

识别欺骗干扰的具体样式是实现抗欺骗干扰的前提,只有率先对干扰的类型进行辨别,采取相应的措施,才能够有效地实现抗干扰。近年来,国内外针对欺骗干扰的识别技术有了一定的进展。李建勋等通过对接收信号进行双谱分析,并提取双谱切片的方差和信息熵等作为特征参数,取得了很好的识别效果。史忠亚等通过在频谱和双谱域两种变换域中提取特征参数,将特征输入神经网络进行分类,并利用遗传算法对径向基(radial basis function,RBF)神经网络的权值和阈值进行优化。但是,上述方法中雷达信号均为单频信号,对于目前广泛应用的线性调频(linear frequency modulation,LFM)信号的识别效果未知。Tian等通过构造积谱矩阵,利用非负矩阵分解(nonnegative matrix factorization, NMF)的方法对矩阵进行分解,对分解后的向量提取特征值,实现了对欺骗干扰的识别。李艳莉等通过对接收信号进行积谱运算,利用局部二值模式对积谱矩阵提取旋转不变特征,从而将图像处理的方法应用到欺骗干扰识别中。结果显示上述方法的识别率还有提升空间。卢云龙等利用DRFM在相位量化阶段产生的谐波效应,通过分数阶傅里叶变换对接收信号的调频率进行检测,通过与目标回波进行对比,从而实现欺骗干扰的识别。该方法在识别出具体的干扰形式方面还需要进一步拓展。有些学者利用时频分析的方法对信号进行变换,通过分析时频域图像特征对欺骗干扰信号进行识别,但是这类方法在低信噪比情况下信号特征容易被噪声湮没,失去识别能力。随着目前分类器的性能不断提升,欺骗干扰信号的识别能力有了进一步的拓展,Zhou等将贝叶斯决策理论应用于欺骗干扰识别领域,通过特征融合的方式增强识别效果。Shao等利用改进的一维卷积神经网络(one-dimensional convolutional neural network, 1D-CNN)以及2D-CNN对几种常见的干扰信号进行识别。此外,一些其他的机器学习模型也正在运用于欺骗干扰识别领域。除了欺骗式干扰的识别,目前针对压制干扰类型识别或是对于频谱弥散(smeared spectrum, SMSP)和切片组合(chopping and interleaving, C&I)等新型干扰识别的研究也在进行,这些有源干扰识别方法都是通过对信号进行变换后提取特征进行识别,也是目前有源干扰识别领域最主要的方法,均取得了很好的识别效果。

为了能够更加有效地利用目标回波和欺骗干扰信号在不同频段上的信息差异,本文提出了一种基于稀疏表示分类的方法实现对距离拖引干扰(range gate pull off, RGPO)、速度拖引干扰(velocity gate pull off, VGPO)和距离-速度同步拖引干扰(range-VGPO, R-VGPO)的分类识别,利用不同慢时域接收到的信号,分析不同频段上信号参数的变化情况,通过计算三阶累积量切片来增强系统抗噪性并进一步凸显不同信号的差异;通过奇异谱分析对信号特征进行压缩,利用特征的分解向量构造字典进行稀疏表示分类(sparse-based representation classification, SRC)。最后对每一个频段的识别结果进行决策融合,得到最终的识别结果。经验证,该方法在低信噪比下具有较高的干扰识别率,在信噪比为0 dB时平均识别率能达到90%以上,在信噪比为7 dB时,识别率基本接近100%,通过与文献[16]和文献[31]提出的方法进行干扰识别率对比,证明了该方法的优越性。

1 信号模型

设雷达采用LFM发射信号:

(1)

式中:()=jπ(2+),为中频频率,为调制斜率;为发射信号初始相位;为脉冲宽度。

假设有一点目标位于距离雷达处,雷达目标回波信号为

(2)

式中:为回波信号的幅度;c为光速。

当DRFM干扰机实施RGPO时,干扰信号RGPO和目标回波会发生相干合成,雷达接收到的合成信号为

(3)

式中:为RGPO干扰的幅度；Δ为干扰机对雷达信号进行接收、存储、处理、转发所需的固有延迟；Δ()为RGPO的调制时延；为干扰机干扰信号初始相位。

当DRFM干扰机实施VGPO时,干扰信号VGPO和目标回波会发生相干合成,雷达接收到的合成信号为

(4)

式中:为VGPO的幅度；Δ()为VGPO调制的多普勒频移。

当DRFM干扰机实施R-VGPO时,干扰信号R-VGPO和目标回波会发生相干合成,雷达接收到的合成信号为

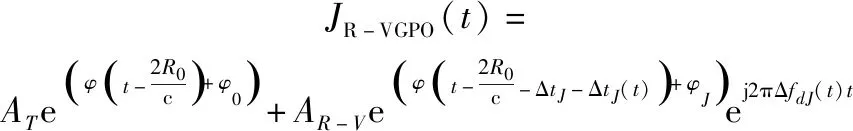
(5)

式中:-为R-VGPO的幅度。

2 累积量特征矩阵

2.1 小波包分解

为了识别上述列出的雷达目标回波信号以及欺骗干扰信号,本文提出了一种基于多时域多频段的新型识别方法。在一个脉冲重复间隔(pulse repetition interval,PRI)内,利用小波包分解的方法,将接收到的信号分解成带宽相等的多个信号。

通过对频率的分解,一方面能够对接收的信号进行进一步的滤波,减少噪声的影响;另一方面,由于欺骗干扰信号与目标回波相比,在波形上非常相似,通过频段的划分,能够更加细致地分析不同信号在固定频段上的变化情况。在本文提出的方法中,对接收到的信号进行3层小波包分解,即可得到8个不同的频段分解信号,每个频段的带宽相同,如图1所示。

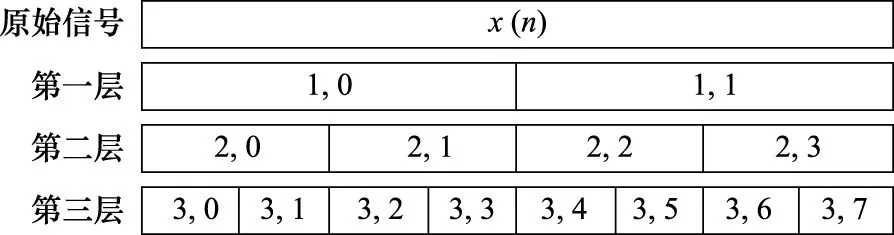
图1 接收信号在不同频段上分解Fig.1 Received signals decomposed in different frequency bands

对于各种拖引干扰信号,其参数一般是随着时间变化的,为了进一步区别不同欺骗干扰信号的参数变化情况,将一定时间内不同PRI接收到的信号进行小波包分解,可以写成:

=[(,),(,),…,(,),…,(,)]

(6)

式中:表示第个小波分解频段上的信号集合；=1,2,…,8;表示慢时域,=1,2,…,;(,)为第个频段上慢时域时刻所接收到的信号向量,对应不同的欺骗干扰信号,接收信号(,)有以下几种情况:

(7)

2.2 构造累积量特征矩阵

高阶累积量在欺骗干扰识别领域有着广泛的应用,由于高阶累积量对于噪声有很好的抑制作用,并且可以很好地表现信号的非线性特征。因此,将上述分解得到的多个频段的信号进行三阶累积量运算,能够进一步体现不同欺骗干扰信号与目标回波之间的差异。由于雷达的周期性,进入雷达接收机内部的目标回波和欺骗干扰应为循环平稳随机过程,定义时变三阶累积量为

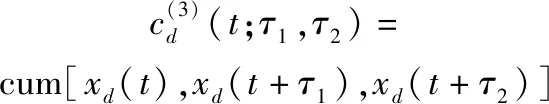
(8)

式中：、分别为延时量；cum表示累加运算。目标回波信号和几种欺骗干扰信号的累积量三维图如图2所示。

图2 信号累积量三维图Fig.2 3D images of the cumulant of signals

与双谱类似,三阶累积量具有对称的性质,因此在对三阶累积量进行分析时,可以只提取其对角切片特征,能够提高运算速度,三阶累积量的对角切片为

(9)

对目标回波信号与几种欺骗干扰信号进行三阶累积量变换,取对角切片后的结果如图3所示,通过图3横向对比可以看出,对4种信号的累积量取对角切片,可以更好地凸显不同种信号的差异,同时能够有效地减少计算时间,提升运算效率。对于第个频段上接收到的信号集合,对每一个慢时域时刻进行三阶累积量计算,则可以得到在第个频段上信号的稳定变化特征,所得到的特征矩阵可以写成以下形式:

=[(′,),(′,),…,(′,),…,(′,)]

(10)

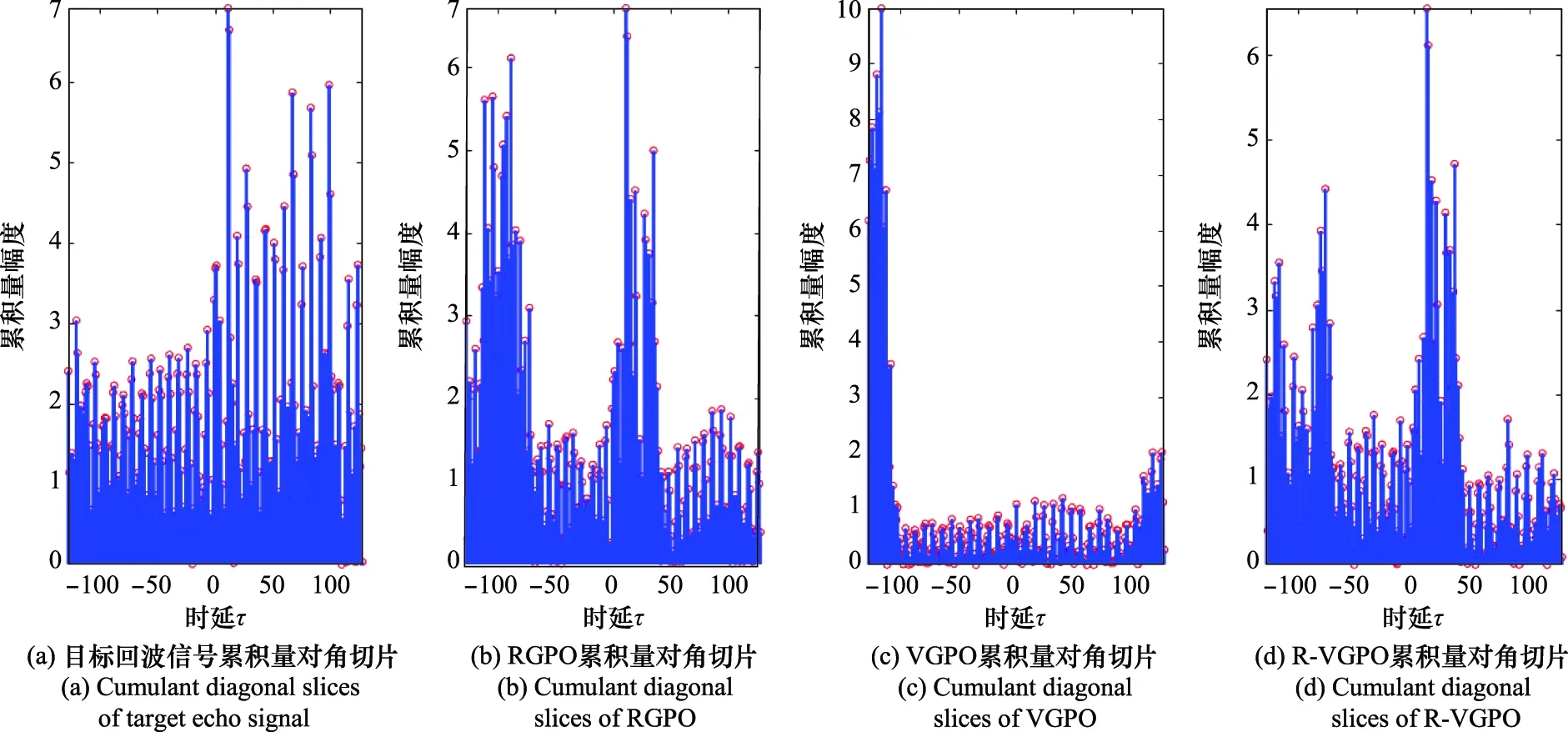
图3 累积量对角切片Fig.3 Cumulant diagonal slices

特征矩阵是通过对接收信号进行三阶累积量变换后获得的,可以有效减少噪声的影响;又由于特征矩阵事先进行了频段划分,且包含不同脉冲重复周期的信号分量。因此,特征矩阵含有稳定的信号参数变化信息,可以从时域和频域两方面刻画信号的特征,从而增强识别系统的稳定性。

2.3 特征矩阵的奇异值分解

每一个频段的特征矩阵,包含了不同时刻PRI下的参数变化情况,但是在处理这些参数时,并不希望利用矩阵的全部参数进行分类识别。因此,对于每一频段特征矩阵,利用奇异值分解的方法进行处理,一方面是因为这样可以减少后续识别的计算量,提高识别效率;另一方面是可以在损失少量信息量的情况下,将不同脉冲重复周期信号的累积量信息进行压缩,进一步提取特征,减少特征信息的冗余度。

奇异值分解被广泛运用于机器学习中进行数据降维,压缩特征信息,在欺骗干扰识别领域也有一定的应用。对每一个频段上大小为×的特征矩阵,其中表示慢时域的长度,为接收到的累积量切片长度,根据奇异值分解公式,有

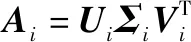
(11)

式中：=[1,2,3,…,,…,]为特征矩阵的左奇异矩阵,为×1的左奇异向量,=1,2,3,…,；=[1,2,3,…,,…,]为特征矩阵的右奇异矩阵,为×1的右奇异向量,=1,2,3,…,;为×的对角矩阵,包含了特征矩阵的分量信息,可以写成如下形式:

(12)

表示矩阵的奇异值,反应了矩阵的固有特征,其中=1,2,3,…,min(,),且满足1>2>3>…>min(,)。因此,可以写为

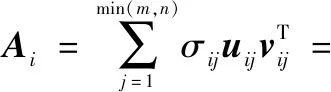
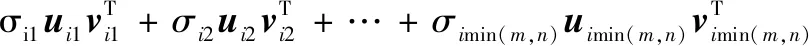
(13)

一般情况下,矩阵的奇异值中只有少量数值较大的奇异值,其余的奇异值均接近或等于0,所以特征矩阵主要分量决定于数值大的奇异值所对应的奇异向量。因而通过分析少量的奇异值即可把握的整体信息,实现数据的降维。通过对特征矩阵进行奇异值分解,得到较大奇异值对应的左右奇异向量、。由于目标回波信号属于单分量信号,且目标回波和欺骗干扰信号结构具有相似性,因此其特征矩阵的奇异值分布中第一个奇异值在数值上远远大于其他奇异值,图4展示了在单一频段上不同种信号的奇异值分布情况。

图4 第六频段特征矩阵奇异值分布Fig.4 Singular value distribution of feature matrix in the 6th frequency band

3 稀疏表示分类算法

稀疏表示分类算法是将稀疏表示的理论用于分类识别中,首先构造过完备的冗余函数字典,字典中的元素称为原子,稀疏表示就是从字典中找到具有最佳线性组合的少量原子去表示一个样本,利用字典的冗余性可以很好地捕获未知样本的本质特征,从而进行分类识别。稀疏表示分类基于一个假设,即同类的样本间线性关系强,而不同类的样本间线性关系较弱。因此,使用过完备字典去表示一个未知样本时,其结果往往容易被表示为字典中的同类原子的线性组合。

设=[,1,,2,…,, ,…,,]是由第类样本组成的一个集合,其中, ∈,表示向量的维度,表示第类样本的数量。若集合是过完备的,则任意一个不属于集合的第类样本都可以用中的元素进行表示:

=,1,1+,2,2+…+,,

(14)

因此,可以通过集合来表示,即=,其中=[,1,,2,,3,…,,]是样本在集合形成的线性表示系数。现有=[,,…,,…,],其中表示总类别数目,是各类别样本的过完备集合,称为字典。给定一待测样本∈并假定其属于第类,则样本可在上展开:

=

(15)

式中:=[0,0,…,0,,1,,2,,3,…,,,0,…,0,0]是样本在字典上形成的稀疏表示。的非零项与字典中第类原子相对应,为了得到的非零项系数,可通过求解正则式的最小值,将问题转化为求解最优化问题:

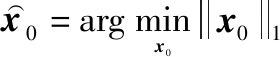
(16)

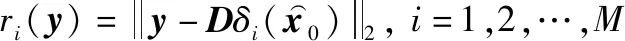
(17)

(18)

在本文提出的方法中,雷达接收信号提取特征向量后在字典上展开,稀疏表示系数中非零项所对应的原子与样本有相似的结构,代表该样本信号与这些原子所对应的信号类型有相似的参数变化规律,根据这一特性,能够有效确定雷达接收信号所属的类别。

4 实验结果与分析

本文提出了一种基于稀疏表示分类的欺骗干扰识别算法,通过接收不同慢时域下的信号形成信号集合,利用小波分解重构的方法对接收到的信号进行频段的划分,得到不同频段上的信号分量;计算各个频段上的三阶累积量切片以获得不同频段上信号的稳定特征,凸显不同种信号间的差异;接着通过奇异值分解的方法对特征矩阵进行降维,减少信号分类识别的运算量并提取矩阵的主要特征分量。然后通过构造过完备字典,对提取的奇异向量进行稀疏表示分类,得到在每一个频段上的分类识别结果。最后通过决策融合的方式实现最终信号的分类。整个算法流程图如图5所示。

图5 算法流程图Fig.5 Algorithm flow chart

通过奇异值分解得到的奇异向量作为字典的原子,采集大量的样本构造过完备字典,则对于任一新的信号,通过提取特征后得到其奇异向量,都可以在字典上形成稀疏表示,通过稀疏表示分类得到识别结果,对于每一个奇异值,可以分解为左右两个奇异向量,在利用稀疏表示分类进行识别时,可以将左右两个奇异向量分别构造字典进行识别。由于每个频段只需分解一个奇异值,对于个频段,一共可以构造2个字典。每一个字典进行稀疏表示分类都可以得到一个识别结果,最后通过决策融合的方式得到接收信号的最终分类结果。

仿真实验中,信号参数设置如下:雷达发射波形为LFM,脉冲宽度为20 μs,信号带宽为5 MHz,采样频率为20 MSPS(million samples per second, 即每秒采样个数,以百万次作为单位);DRFM干扰机的固有延时为200 ns,RGPO的拖引速率为1 000 m/s,VGPO的拖引速率为50 kHz/s;为了达到欺骗的效果,干扰信号的幅度一般为雷达回波信号的1.3～1.5倍,因此本文中取干信比为3 dB。为制作用于稀疏表示分类的超完备字典,每种信号进行250次仿真实验,信号进行三层小波包分解划分为8个频段,所得到的信号集合慢时域长度为50,每个频段制作2个过完备字典,每个字典容量为1 000。

取新的样本利用字典进行分类识别,将待测信号的特征在字典上展开,结果如图6所示。其中,序号为1～250的原子为目标回波的特征向量,序号为251～500的原子为距离欺骗干扰的特征向量,序号为501～750的原子为速度欺骗干扰的特征向量,序号为751～1 000的原子为距离-速度欺骗干扰的特征向量。图6(a)中,目标回波信号与字典上匹配度最高的原子类别为目标回波,且只有该原子位置上的稀疏表示系数较大,表明该样本信号与此原子对应的目标回波信号有相似的参数变化规律,是属于同一类别的信号。在识别过程中,通过对比不同类别原子对样本信号的还原能力,实现对样本信号的识别。在图6(b)～图6(d)中,稀疏系数较大的值通常集中在与样本同类的原子上,与其他原子相比,这些原子重构的信号与样本信号有更高的相似度,因此能够实现较为准确的干扰信号识别。

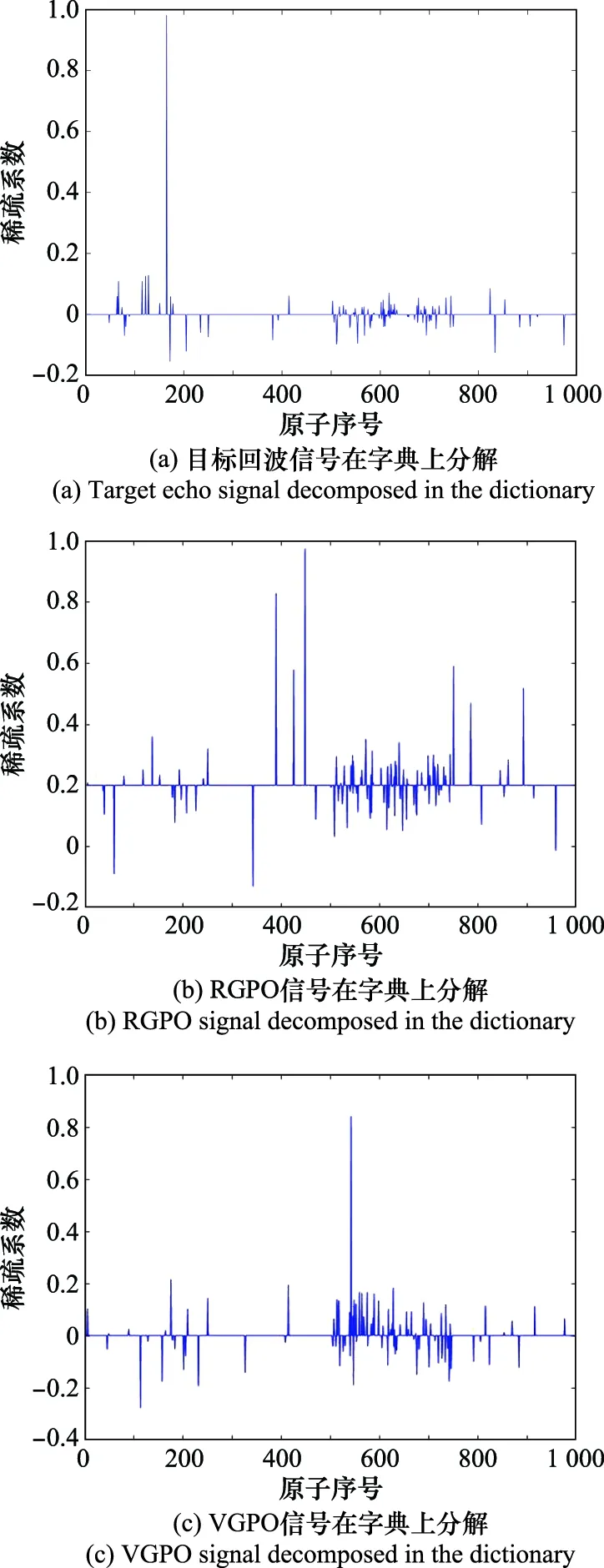
图6 接收信号在字典上展开Fig.6 Received signal decomposed in the dictionary

对于每一个字典,在进行SRC后都可以得到一个分类结果,最终的输出结果用投票原则进行整合:

=arg max([,,,])

(19)

式中:、、、分别表示识别为目标回波、RGPO、VGPO以及R-VGPO的字典数目,整合后的识别结果为各个字典识别后出现次数最多的信号类型。通过大量的实验测试,发现第2、3、4频段在各个信噪比上都有较好的识别效果。因此,通过筛选频段后,对信噪比为-6～10 dB的信号进行了测试,每个信噪比进行300次SRC仿真,识别结果如图7所示。

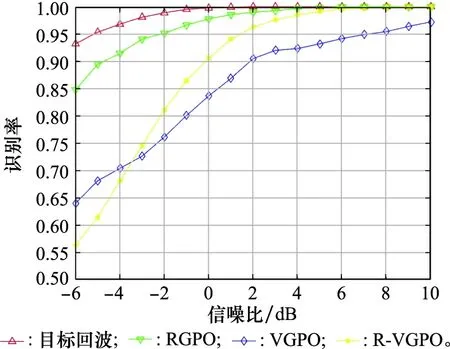
图7 各个信号SRC识别率Fig.7 SRC recognition rate of various signals

通过验证,在信噪比为4 dB时,除VGPO外,其他干扰识别率均可以接近100%,信号的平均识别率在信噪比为7 dB时基本稳定,总体上能够保持在一个较高的识别水平。

进一步验证,测试不同距离拖引速率和速度拖引速率对识别率的影响,分别测试距离拖引速率在600 m/s、800 m/s、1 000 m/s以及1 200 m/s下信噪比为0～8 dB的平均识别率,以及速度拖引速率在40 kHz/s、50 kHz/s和60 kHZ/s下信噪比为0～8 dB的平均识别率,结果如表1和表2所示。

表1 距离拖引速率的影响Table 1 Influence of range pull off rate

表2 速度拖引速率的影响Table 2 Influence of velocity pull off rate

从表1和表2可以看出,不同的拖引速率对于识别结果没有产生太大影响,0 dB时平均识别率均能达到90%以上,识别结果较为稳定,对于不同拖引速率参数的欺骗干扰信号均能有效识别。同时,将本文的方法与文献[16]以及文献[35]的方法在相同的欺骗干扰参数条件下进行对比,结果如图8所示。

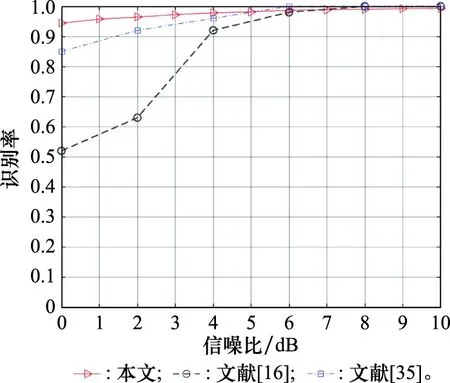
图8 识别率对比Fig.8 Recognition rate comparison

通过对比,本文的识别方法在低信噪比(≤5 dB)下有更高的识别率,能够有效降低噪声的影响,整体识别率上优于其他两种方法。仿真实验证明了基于稀疏表示分类的欺骗干扰识别相较于其他方法,具有更好的识别效果。

5 结 论

本文提出一种基于稀疏表示分类的欺骗干扰识别方法,该方法通过分析不同频段上的信号变化情况,提取三阶累积量切片特征来增强系统抗噪声性能,利用奇异值分解的方法对特征进行压缩,加快识别效率并能在一个频段上构建2个字典进行稀疏表示分类。将不同频段的分类结果进行决策融合,得到最终的识别结果。与其他欺骗干扰识别算法相比,所提出的算法在低信噪比下具有更高的识别率,有更好的抗噪声性能。