全息穿透雷达非平整表面杂波抑制算法研究

陈 诚, 刘 涛, 曹来保, 何志华, 黄春琳, 粟 毅

(国防科技大学电子科学学院, 湖南 长沙 410073)

0 引 言

得益于电磁波对介质的穿透能力、非接触的测量方式和有效获取目标散射特性的能力,全息穿透雷达(holographic subsurface radar,HSR)已在无损探测领域中展现出巨大潜力。区别于探地雷达(ground penetrating radar,GPR)与穿墙雷达(through-the-wall radar,TWR),HSR使用的工作频段更高,能对几何尺寸更小(厘米级甚至毫米级)的浅埋目标实现高分辨率成像,且系统制作成本更低。然而,现有的HSR成像算法往往对平面介质模型适应性较好,而对非平整表面介质中埋藏目标成像效果欠佳。而又因为其工作频段较高,实际探测时介质表面的较小起伏相对于波长而言,已经足够在成像结果中形成严重杂波干扰,因此研究非平整表面杂波抑制方法是HSR系统发展的重要方向。

目前,针对HSR穿透非平整表面介质成像中杂波干扰的研究相对较少。一种直接的方法是使用与介质电磁特性相近的柔性材料将非平整表面填平,再应用目前已发展成熟的算法进行成像处理,但在实际应用中获取相匹配的填充材料较为困难;利用射线追踪技术,可以在雷达扫描时测量出非平整表面的几何参数,通过仿真软件可以估算出表面回波并进行去除,这种方法的局限性在于表面回波测量以及仿真结果与实际数据通常存在较大误差。区域均值对消法(subdomain mean cancellation,SDMC)将扫描区域划分为适量子区域,对每个子区域进行均值对消处理,但该方法对表面粗糙度大且起伏无规律的介质的适用性较差。谱域滤波法(spectral domain filtering,SDF)基于雷达回波中目标与介质谱域分布特性差异实现杂波抑制,适用于去除锥面、柱面等旋转对称曲面回波,但如果目标是线状且沿母线方向分布,会在谱域滤波时对目标谱信息造成大量损失,从而影响成像质量。文献[25]提出通过回归分析方法解析出连续缓慢变化的非平整表面函数,然而实际应用中的表面往往是随机起伏,甚至存在非连续表面,此时无法获取到适用的解析函数。采用共形天线阵或共形合成孔径扫描能够在特定场景有效改善成像效果,如通过半球形模型表面共形阵列天线对乳房进行成像扫描,实现早期乳腺癌检测以及安全检查时,采用圆柱面扫描对人体隐藏武器进行排查。但这类方法仅限于特定目标检测,应用范围较窄。

鉴于上述方法的局限性,本文提出一种基于双频对消(double-frequency cancellation,DFC)的非平整表面杂波抑制方法。该方法通过获取高低两种频率下的雷达回波数据,分别建立两种频率下的回波信号模型,结合不同频率雷达回波中目标信号与非平整表面特性差异,通过理论推导估算出表面回波与原回波对消,实现非平整表面杂波抑制,并提出了减小估算误差的可行思路,最后通过仿真与实测数据,定量和定性地分析了实验结果,表明本文方法能够有效抑制非平整表面杂波。

1 DFC模型

对于HSR系统,接收到的雷达回波通常由目标回波与杂波组成,特别是在进行非平整表面介质中目标探测时,杂波主要表现为非平整表面回波以及天线之间的直耦波,其中直耦波可通过录取系统对空数据进行去除。因此,设某时刻雷达天线位于(,),表示扫描水平面横向坐标,表示纵向坐标,记此时采集低频条件下获取的雷达回波为,可以构建与时间相关的回波模型如下:

()=cos[(-)+]+cos[(-)+]

(1)

式中：第一项表征表面回波;第二项表征目标回波;和分别表示表面与目标回波的幅度;和分别表示表面与目标回波时延;为低频信号频率;表示系统初始相位。那么,高频条件下天线处于同一位置时回波模型可以同样表示为

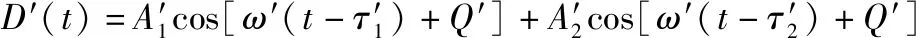
(2)

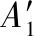
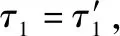
=cos(-)+cos(-)

(3)

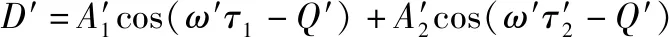
(4)

再经同相-正交(inphase-quadrature, IQ)解调后输出,可表示为

=ej( -)+ej( -)

(5)

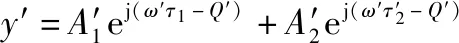
(6)

通过系统校准,可以去除系统初始相位和′的影响,从而输出简化为

=ej +ej

(7)

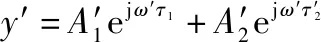
(8)

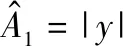
(9)

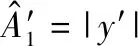
(10)

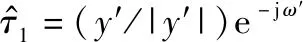
(11)

那么,可以根据上述参数拟合出表面回波的近似值:

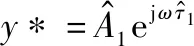
(12)

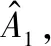
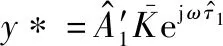
(13)

然而,通过单一频点数据来估算时延,存在距离模糊问题,即

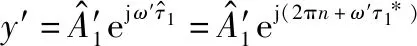
(14)

式中:为整数。

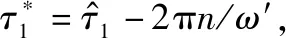
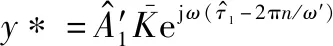
(15)

为解决不能估计出所带来的模糊,可在系统设计时将高频设计为低频的整数倍,以2倍为例,即′=2,则可将上述不可解模糊简化为二相模糊,即

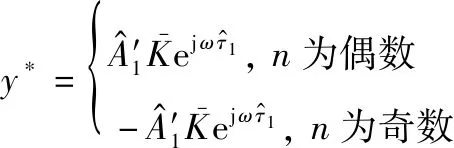
(16)

将原回波与拟合回波对消,可得

(17)

由于≪,因此可通过比较|-|与||的大小来判断的奇偶性,即

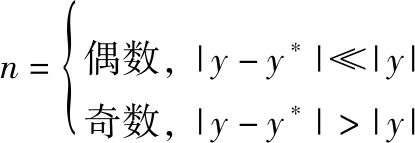
(18)

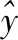
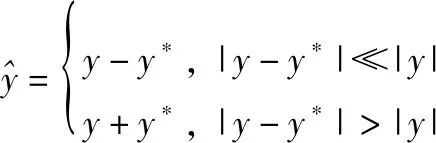
(19)

最后,对回波矩阵逐点进行DFC处理后,使用全息成像算法获得成像结果,对于结果中由估计误差引起的残留杂波,可结合文献[30]中提出的成像增强算法处理,可在增强目标的同时进一步抑制图像中残留的杂波。

2 实验与分析

这里通过仿真和实测实验两种方式对所提方法进行验证,并定量和定性地分析了本文方法在抑制非平整表面杂波方面的有效性。

2.1 仿真实验设计

仿真实验数据通过CST电磁仿真软件录取,实验目标为一相对介电常数为2.8的塑料圆柱,其半径=25 mm,高=30 mm,埋藏于相对介电常数为2.44的干燥土壤中,埋藏深度=30 mm。天线距土壤表面40 mm沿水平面进行扫描,扫描面大小为200 mm×200 mm,步进间隔为10 mm,发射信号频率分别为5 GHz和10 GHz。仿真实验场景如图1所示。

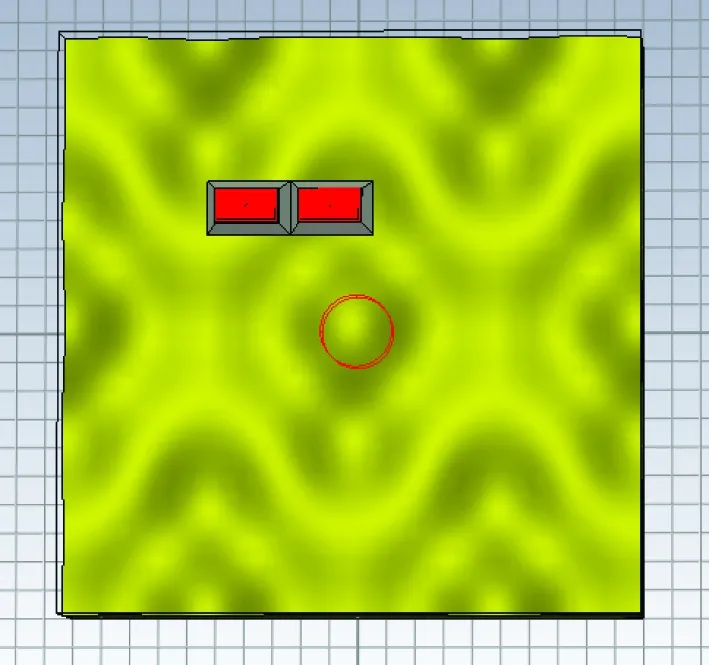
图1 仿真实验场景示意图Fig.1 Schematic diagram of simulation experiment scenario

2.2 实测实验设计

实测数据通过本课题组设计的穿透成像实验系统获取,该系统由矢量网络分析仪(安捷伦 N5230C)、精确定位二维移动扫描平台、接收天线、发射天线及上位机组成。其中,发射与接收天线安装在移动扫描平台上,通过上位机控制平台的移动与矢量网络分析仪数据的接收和处理,实验场景如图2所示。

图2 实测实验场景图Fig.2 Schematic diagram of real experiment

实验采用的介质为一块厚度为35 mm的非平整丙烯腈/J二烯/苯乙烯共聚物(Acrylonitrile Butadiene Styrene, ABS)塑料板,其表面最大高程差为15 mm,如图3所示。在其背面分别布设有一枚一元硬币与一金属圆环作为目标,圆环内外半径分别为20 mm与40 mm,图4展示了两目标的外观与详细位置关系。实验系统采用的扫描频率范围为10～20 GHz,频段内共计1 001个频点,在频率范围内均匀分布。天线距离介质表面最高点约10 mm,扫描区域范围为300 mm×300 mm,采样间隔为5 mm。实验中使用的低频为10 GHz,高频为20 GHz。

图3 实验介质Fig.3 Experimental medium

图4 实验目标Fig.4 Experimental targets

分别通过仿真与实测实验系统获取回波数据,对上述数据分别通过SDF、SDMC及DFC等处理,仿真实验结果与实测结果分别如图5和图6所示。

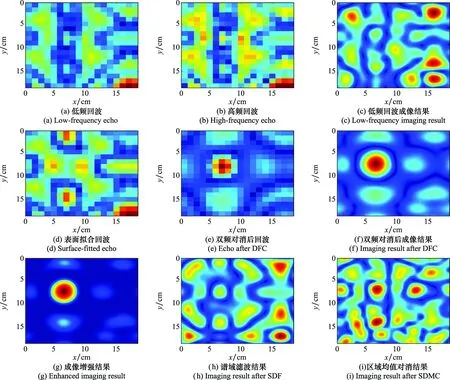
图5 仿真实验结果图Fig.5 Simulation imaging results

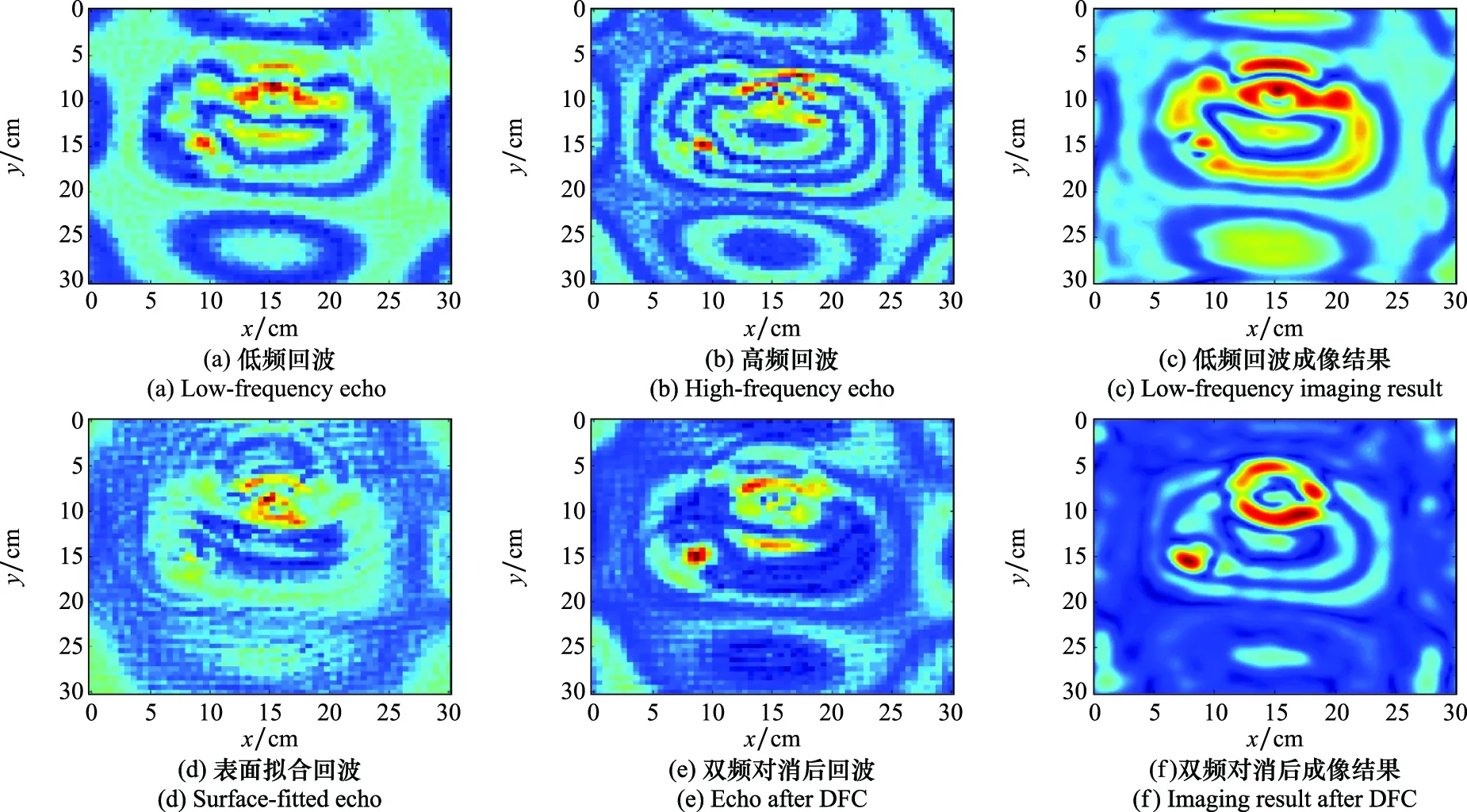
图6 实测实验结果图Fig.6 Real experiment imaging results

2.3 实验结果与分析

图5列出了仿真实验数据经各类处理前后的结果图。通过仿真获取的原始低频、高频回波分别如图5(a)和图5(b)所示,对低频回波直接进行成像处理,得到成像结果图5(c),从上述结果图中均无法辨识目标,可以看出土壤非平整表面回波完全将目标回波掩盖;图5(d)为通过本文方法拟合出的表面回波,图5(e)为将拟合回波与原始低频回波对消后的结果,从对消后回波中已经可以分辨出目标轮廓,处理后回波成像结果如图5(f)所示,图中可以清晰观察出目标的形状与尺寸,且与实际目标参数相符,证明了所提方法抑制杂波的有效性。在此基础上利用成像增强算法进行处理,可在增强目标的同时进一步抑制图像中的残留杂波,如图5(g)所示。SDF和SDMC处理后成像结果分别如图5(h)和图5(i)所示,两幅图像中均难以分辨出目标图像,表明两种方法在处理起伏剧烈的非平整表面时效果欠佳。

图6为对实测数据进行上述处理前后的结果,其中图6(a)和图6(b)分别为通过系统获取的低频和高频回波,从图中可以看到明显的非平整表面回波轮廓;低频成像结果如图6(c)所示,尽管成像结果中能看到部分目标,但由于强表面杂波干扰,已无法辨识出目标具体形状;图6(d)～图6(g)为DFC处理各阶段的结果,尽管DFC后回波与成像结果仍残留部分杂波,但成像结果中已经可以分辨出目标为一环形与一圆形,结合增强成像处理后可进一步抑制残留杂波得到更清晰的目标图像;图6(h)为SDF后的成像结果,与处理前对比改善有限,这是由于SDF方法主要应用于锥面、柱面等旋转对称曲面杂波抑制,对非对称表面适应性较差;SDMC处理后成像结果如图6(i)所示,可以看出该方法对目标区域外的杂波抑制效果较好,但目标区域并未改善,这是由于均值对消过程中部分目标回波信息也被对消,从而导致成像结果中目标信息丢失。

为了进一步量化评估各方法的抑制杂波性能,表1记录了仿真与实测数据经各种方法处理前后成像结果的目标信杂比(signal-to-clutter ratio,SCR),即图像目标区域平均功率与杂波区域平均功率的比值,其定义为

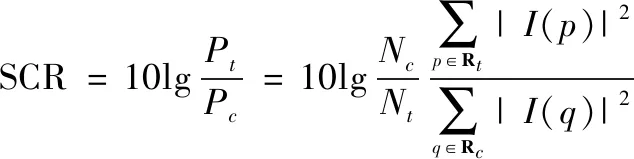
(20)

式中:表示目标区域平均功率;表示杂波区域平均功率;和分别表示目标和杂波区域;和分别表示目标和杂波区域内像素点个数;()和()分别表示目标和杂波区域各点的像素值大小。

表1 不同方法处理后成像结果SCR参数Table 1 SCR of imaging results processed by different methods dB

从表1中的SCR评价指标来看,无论是应用于仿真还是实测数据,采用DFC方法都能够较好地抑制成像结果中的杂波成分,在此基础上结合成像增强方法后能够更显著提升成像结果中的SCR,达20 dB以上。SDMC对SCR提升程度相对较小,约3～4 dB。SDF应用于该类复杂非平整表面时几近失效,甚至在处理仿真数据后SCR有所降低,表明DFC方法更适用于实际非平整介质内无损探测。

3 结 论

本文提出了一种基于DFC的非平整表面杂波抑制方法,通过获取高低两种频率下的雷达回波数据,利用不同频率雷达回波中目标信号与非平整表面特性差异来拟合表面回波实现对消,并结合仿真与实测数据验证了该方法抑制非平整表面杂波的有效性。值得注意的是,实验系统高频、低频回波均采用同一天线通过矢量网络分析仪获取,而在实际应用中需尽量保持高频与低频天线辐射区、波束宽度与辐射角一致以减小系统误差。