基于AHP-模糊综合评价法的地质实习成绩评定方法构建

姜春露，张文媛，郑刘根，赵 田

(1.安徽大学资源与环境工程学院，安徽 合肥 230601；2.生态与环境国家级实验教学示范中心，安徽 合肥 230601)

引言

地质学是一门实践性很强的学科，对于地质类专业的学生来说，地质野外实习是其将所学课堂知识与现场地质现象相结合，开阔地质眼界、增强动手能力、提高野外工作技能的必修课。同时，对学生的爱国主义教育及专业道德品质的提高也起着重要作用。地质学专业实习主要有地质认识实习、区域地质填图实习和生产实习等，这些实习是由野外的地质实习与室内报告的整理撰写结合完成，学生的实习成绩是以实习报告的成绩为主，一定程度上反映学生的野外实践能力。然而，近年来的教学实践发现，目前的学生实习成绩评定方法存在一些不足，主要表现在：一是野外实习期间一些学生不认真观察和记录，回到室内后抄袭实习指导书或他人记录本内容，无法真实反映学生野外实习期间的真实情况；二是实习报告中引用过多的教科书、前人实习报告、他人报告上内容，实习报告的编排几乎千篇一律，对实习总结报告评判标准过于单一；三是对学生野外实习环节的表现重视不够，最终成绩评定存在较大的主观随意性等。这些问题使学生实习成绩评定的合理性受到一定影响，同时也使指导教师无法准确掌握实习效果。因此，有必要探索一种客观合理的地质认识实习成绩评价方法。

为解决地质野外实习考核中存在的上述问题，本文着眼系统思维，利用层次分析法(AHP)及模糊综合评价方法，构建科学合理的实习成绩评定体系，再通过模糊运算得出学生的最终实习成绩，这样可对学生的实习进行科学合理的量化评定，并对教师教学效果的检验及教学水平的提高提供有力保障，最终达成“教”与“学”，“学”与“习”互促互进。

一、基于AHP方法构建地质实习成绩评价体系

(一)评价指标体系层次结构模型

根据地质实习的形式及学生获取知识的方式，参考相关研究成果结合专业教师访谈方式，建立了学生地质实习成绩评定的指标体系。本文建立的实习成绩评价体系由4个一级指标和15个二级指标组成，具体指标及其权重如图1、表1所示。

表1 评价体系指标及其权重表

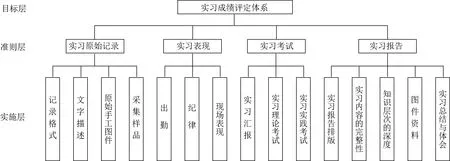
图1 评价体系

(二) 指标权重的确定

根据比较判断矩阵的构造方法，通过对实习成绩评定指标体系中的各具体指标的重要性进行两两比较，采用判断矩阵量表的“1-9”标度法。通过问卷调查的方式邀请有关专家、教师、学生等对各个指标进行评价，进一步采取德尔菲法(专家调查法)确定参评因素和各项指标在地质实习成绩评定中的权重，进而得到各层次的判断矩阵。具体步骤为：选择专家以八至二十人为宜，向专家提供资料，专家组根据自己的知识和经验对各指标作出评价。充分考虑专家意见后说明预测值的评判依据和理由反馈给专家，请专家检验并提出适当修改意见，进行第二次预测，如此反复。将收集到的数据进行整理、归纳，最终经过调整得到判断矩阵。

利用Python软件求解判断矩阵，得到最大特征值λmax及其对应的特征向量Ai，为了评价特征向量的合理性，需要检验判断矩阵的一致性。经一致性检验后，得到下一层次因素对应于上一层次各因素相对重要性的排序权重，即为层次单排序。将对应的特征向量Ai归一化之后即可得到对应指标的权重。

检验步骤如下：

1)计算一致性指标 CI=(λmax- n)/(n-1)；2) 查找平均随机一致性指标RI[11-12]；3) 计算一致性比例 CR=CI/RI。

当CR< 0.1，通过一致性检验，CR 接近于0，有满意的一致性，否则需对权重A进行修正。实习成绩评价指体系中各指标的计算结果如表2至表6。利用AHP法构建的地质实习

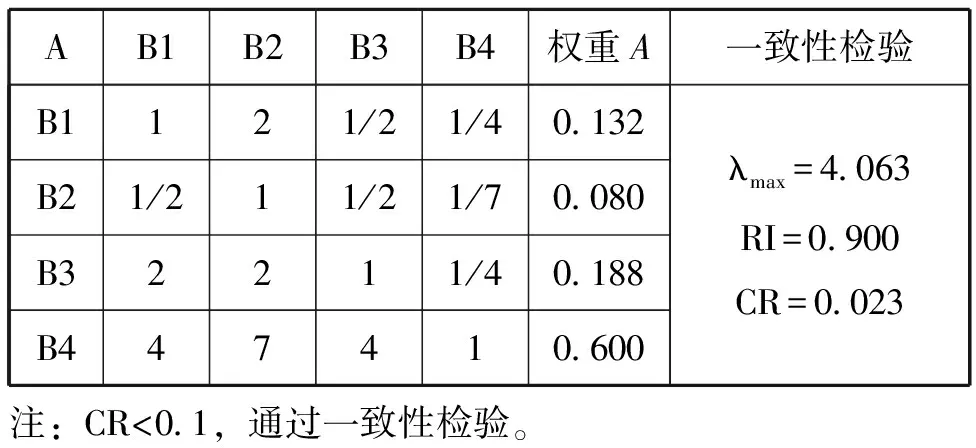
表2 实习成绩评定判断矩阵及一致性检验评价体系中各个指标的权重均通过一致性检验，其权重信息具可信性，为模糊综合评价提供了依据。

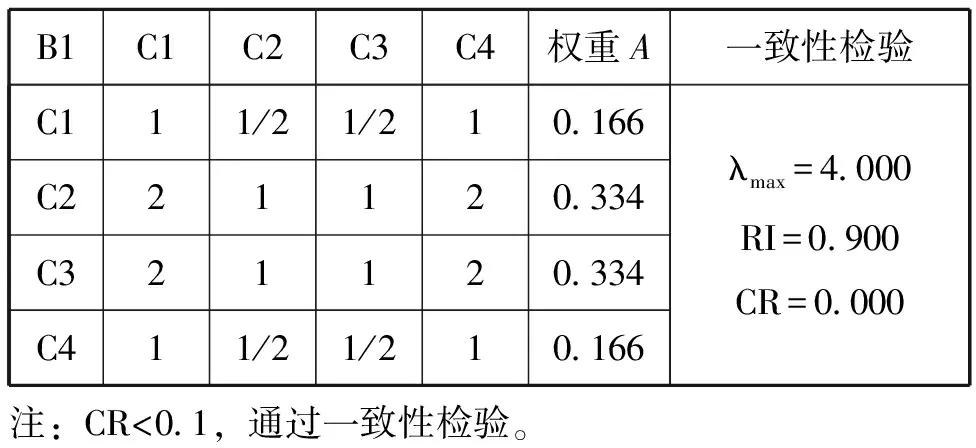
表3 实习原始记录判断矩阵及一致性检验

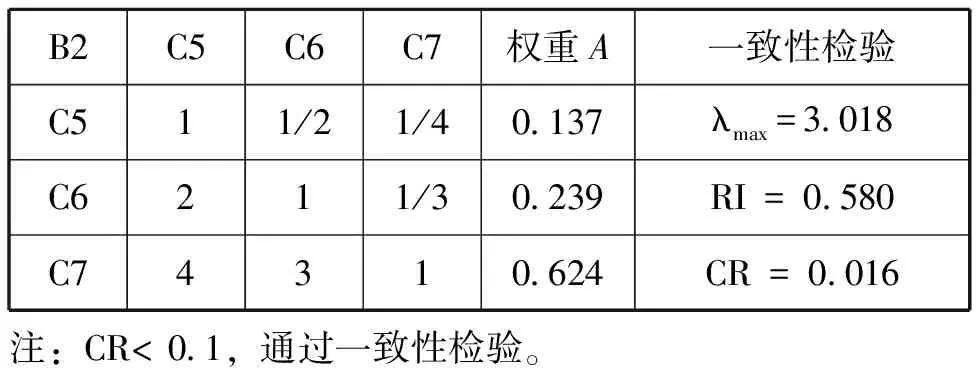
表4 实习表现判断矩阵及一致性检验

表5 实习考试判断矩阵及一致性检验

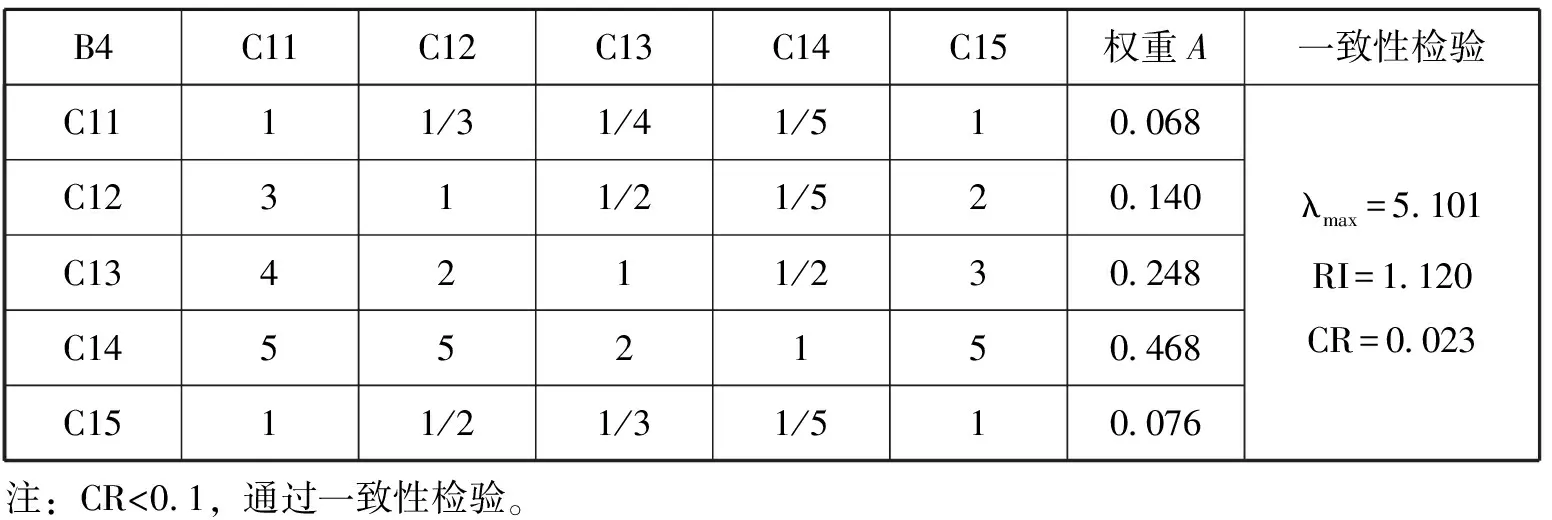
表6 实习报告判断矩阵及一致性检验

二、模糊综合评价模型

模糊综合评价法是根据多因素综合对事物做出合理评价，即利用模糊数学方法建模，进而解决复杂评价问题的一种方法。它可以通过赋值进行定量化，从而将一些定性指标进行量化处理，根据得到的隶属度进行综合分析和比较。主要涉及三个要素：因素集U、评语集V和单因素评价。具体步骤如图2所示，在采用层次分析方法构建实习评价体系并确定各指标权重基础上，采用模糊综合评价方法建立二级指标评价集、权重集、评语集及数值集，构建各级指标模糊矩阵及隶属向量，建立模糊综合评价向量，再输入不同主体对各级指标的评价等级，最后即可得出学生最终实习成绩。所有上述步骤采用JAVA软件编程语言编写代码，在计算机上可自动输出结果。

随后，我又点了上课经常开小差的万超。他说：“通过这幅图片，我发现我的生命是有限的，不能因为年轻就浪费时间、虚度光阴，等到老了追悔莫及。”

图2 基于AHP-模糊综合评价法的地质实习成绩评定流程

(一)建立二级评价指标集、权重集、评语集及数值集

1.根据表1建立评价指标集

U={U1, U2, U3, U4}；U1= {U11, U12, U13, U14}；U2= {U21, U22, U13}；U3= {U31, U32, U33}；U4= {U41, U42, U43, U44, U45}。

2. 根据表2-表6建立权重集

A= {0.132, 0.080, 0.188, 0.600}；A1= {0.166, 0.334, 0.334, 0.166}；

A2= {0.137, 0.239, 0.624}；A3= {0.297, 0.164, 0.539}；

A4= {0.068, 0.140, 0.248, 0.468, 0.076}。

3.建立评语集

本文选取的评语集为优秀、良好、一般、及格、不及格。为验证以学生为本的地质实习成绩评定指标体系评价模型的科学性、合理性和真实性，使其具有适用性和可比性，在此引入三个评价主体，即指导教师、实习学生、实习小组，其权重Wi= (W1, W2, W3) = (0.4, 0.3, 0.3)。

4. 建立数值集

为了给出学生最终的实习成绩，对评语集赋予能反映该评语集重要程度的值，本文选取X= (95, 85, 75, 65, 55)。

(二)建立各级指标模糊矩阵R及隶属向量B

采用逐级上升的递推式模糊评价方法，先对低一级的每个子集中的元素进行单因素评价，得出各个单因素对评语集V的模糊子集，进而模糊关系矩阵R，由模糊运算B= A·R，得到各个模糊子集的隶属度模糊向量，以此类推，得到最终评价结果。

例如，对某个实习生的单因素U11进行评价，实习指导老师、实习生、实习小组的评价分别为优秀(U111)、良好(U112)、一般(U113)，由此可得U11包含的各个单因素的模糊集为：R111= (1,0,0,0,0)；R112= (0,1,0,0,0)；R113= (0,0,1,0,0)；联合以上模糊评价及评价权重，可得U11对评语集V的模糊子集R11= Wi· (R111,R112, R113)T= (0.4, 0.3,0.3,0, 0) ；同理可得U12，U13，U14对评语集V的模糊子集R12；R13；R14，即得U1对评语集V的模糊矩阵R1= (R11, R12, R13, R14)T；又U1对评语集V的隶属向量为B1= A1· R1；同理可求得U2，U3，U4对评语集V的隶属向量B2；B3；B4；可得一级指标U的模糊综合评价矩阵R = (B1, B2, B3, B4)T。

(三)一级指标模糊综合评价向量Bu及最终实习成绩S

已知一级指标权重及其模糊综合评价矩阵，可得其模糊综合评价向量：

Bu=A·R=(b1,b2,b3,b4,b5)

若∑bi≠ 1，则对Bu进行归一化处理可得Bu＇，则根据本文所赋予的数值集X，可得该生最终的实习成绩S=Bu＇·XT。利用JAVA软件，按照模糊评价原理编写计算机代码，只需输入不同主体对各个评价指标评价等级，即可得出学生的最终实习成绩。

结语

本研究基于层次分析法(AHP)综合确定地质实习的成绩评价指标体系，确定各指标的权重并且通过一致性检验，确保各个指标重要程度占比合理科学。运用模糊评定方法，将实习成绩划分为优秀、良好、一般、及格、不及格五个等级，从实习自评，小组评定及指导老师评定三方面综合评价，克服了评价主体的单一性和主观性，很大程度上保证了评定的客观性。

不同实习课程的实习评价体系的构建以及各个指标的重要程度占比可能存在差异，采用AHP-模糊综合评价法的客观性在于各个评价指标程度所占权重均通过一致性检验，这对不同的实习科目以及在其他实践教学课程综合评价具有一定的推广意义。