大连老虎滩海域潮汐调和分析
许秀娥,张容榕,韦冬妮
(1.国家海洋局东港海洋环境监测站,辽宁 丹东 118000;2.国家海洋局大连海洋环境监测中心站,辽宁 大连 116015)
1 引言
潮汐现象是指海水在天体(主要是月球和太阳)引潮力作用下产生的周期性运动,习惯上把海水垂直方向的涨落称为潮汐,水平方向的流动称为潮流。在人类活动比较频繁的近海,海水养殖、海洋运输和海洋工程等涉海产业均与潮汐息息相关,因此开展潮汐运动规律的研究对物理海洋学的发展和国民生产有重要意义。此外,潮汐能也是一种可持续利用的清洁再生能源,潮汐能的开发利用有助于实现碳中和目标。中国近海的潮汐能开发利用潜力以东海最佳,黄海次之。在第四次中国近海可再生能源调查与研究中,辽宁省近海有24个站址入选装机能量达500 kW 以上的潮汐能站址备选资源,仅次于福建、浙江及上海[1]。
大连湾位于黄海北部辽东半岛南端,是我国北方重要的港口。老虎滩验潮站位于大连湾湾口西南,针对渤海开展的潮汐潮流数值模拟大部分以大连外海为开边界,或者利用该站的数据进行验证[2-4]。因此,通过老虎滩验潮站的实测数据分析掌握潮汐运动规律,提高潮汐预报的精度,对于近海海洋活动的安全保障和防灾减灾等具有重要意义。
2 数据及方法
2.1 观测数据
研究数据来源于国家海洋局大连海洋环境监测站老虎滩验潮站的逐时观测潮位。潮位观测资料的时间长短对于其调和分析的结果影响较大,通常只有当观测时段的长度不短于任意两个分潮的会合周期时,这些分潮才能彼此分离。由于不同亚群分潮之间的会合周期最长为一个回归年,所以当观测时段的长度显著短于1 a 时,我们就认为记录是不完整的,因此,潮汐分析时通常选用的时间长度大于1 a[5]。
为此,选取时间长度大于1 a的潮位观测数据开展潮汐调和分析,时间范围为2017 年1 月1 日—2018 年1 月4 日共369 d,时间序列中共包含8 857个逐时潮高[6]。同时,为了对比短期(3 M)潮位资料与长期(1 a)潮位资料调和分析结果的差异,又选用了2017 年3 月1 日—5 月31 日3 M 的潮位观测资料进行分析。对潮位观测数据进行质量控制,异常值或缺测值进行线性插值,进而获取逐时无缺测的完整数据样本,并将时间序列调整为世界时。
本研究采用Foreman程序的自动选取分潮功能进行分潮选取,对于不足1 a 的资料,采用差比法推算随从分潮,将信噪比大于1的分潮作为显著分潮。在获得两个不同时间长度资料的调和常数后,分别对2019 年的天文潮进行预报,并与2019 年的潮位观测资料和国家海洋信息中心发布的潮汐表数据进行对比分析和残差检验。
2.2 分析方法
最初的潮汐分析方法是将潮汐涨落与天体运动直接建立相关关系,这类方法称为非调和法[7]。Newton[8]应用万有引力定律也对地球的潮汐现象进行了解释。根据物理学有关原理可知,任何一种周期性的运动都可以由许多简谐振动组成。潮汐变化是一种非常近似的周期性运动,因而也可以分解为许多固定频率的分潮波,进而求得分潮的调和常数(振幅和迟角),这种分析潮汐的方法称为潮汐调和分析。Darwin 等.[9]此后发展了调和方法,通过对引潮力进行调和展开,得到了主要的潮汐分潮频率。Doodson[10]将引潮势进一步展开为纯调和分潮,引用了月球运动的Brown 系数和Newcomb 表,使引潮势的展开结果更为精准[7]。近年来,随着计算机运算性能的迅速提高,潮汐调和分析的能力和预报的速度得到大幅提升,调和分析法成为潮汐分析和预报的主要方法,非调和法退居次要地位。此后,从计算量中解放出来的科学家更加致力于提升分析和预报的准确度。Amin[11]放弃了传统的交点因子的假设,对19 a 的观测资料进行了分析。方国洪等[12]采用准调和浅水分潮来表示潮汐的高频部分。王晓东等[13]对厦门和东山的潮位资料进行谱分析,求出调和常数,利用分析结果回报两港的潮位,验证了潮汐谱分析对潮汐预报具有一定的应用价值。
Foreman[14]在1977 年开发了一套潮汐分析与预报的Fortran 程序,2002 年Pawlowicz 等[15]将该程序改写成Matlab 程序,命名为T_TIDE 工具箱(以下简称T_TIDE)。T_TIDE 用复数算式代替了传统的实数算式,并增加了随从分潮的推算和非线性误差分析等一些用户自定义界面。2013 年,Matte等[16]在研究潮汐受河流入流影响产生河潮(river tides)而出现的非平稳信号时,在T_TIDE 基础上改进程序从而诞生了NS_TIDE。2018 年,Pan 等[17]利用潮汐调和分析的新方法EHA,开发了工具包S_TIDE。该工具包既可以分析平稳潮,还能分析非平稳潮,进一步完善了潮汐调和分析方法。
老虎滩验潮站位于辽宁省大连市老虎滩渔人码头海港内,北纬38°52′,东经121°41′,四周没有河流汇入,以规则半日潮平稳信号为主,因此用T_TIDE来分析该验潮站数据。
T_TIDE 基于调和分析法可以解析分离一组潮位观测数据中的潮汐和非潮汐信号,最多能分离出45 个天文分潮和101 个浅水分潮,保留了Foreman程序中的自动筛选分潮的方法,用户可根据需要自行添加浅水分潮。T_TIDE 主要针对1 a 及少于1 a的观测资料进行分析,对于少于1 a 的观测资料,用户还可以根据同一群分潮中主分潮与随从分潮之间的振幅比和迟角差,选择利用主分潮来推算随从分潮,例如利用K1推算P1,S2推算K2。对于1 a 以上的时间序列,T_TIDE 进行的交点因子订正计算会不够准确。
T_TIDE 在潮位观测资料分析[18]和模式结果潮汐调和分析[19-20]等方面有着较为广泛的应用。本文利用T_TIDE 对大连老虎滩验潮站一年期和一个季度期两种时间长度的潮位观测数据进行了调和分析,并利用得出的调和常数进行天文潮预报,最后将天文潮预报结果与潮位资料及潮汐表数据进行对比。
3 结果与讨论
3.1 水位功率谱分析结果
谱分析是时间序列在频域上进行分析的方法,亦称频谱分析或波谱分析。考虑到海洋运动无论是时间上还是空间上均存在各种尺度的波动现象,所以频谱分析是分析海洋各种波动现象的常用方法,被广泛应用在海浪谱分析、潮汐和潮流统计预报、海平面长期变化和气候变化研究等各个方面。
利用Matlab 提供的pwelch 程序对老虎滩站2017 年的水位做功率谱分析。pwelch 为常用的功率谱分析函数,相关的参数设置如下:窗函数类型选择hanning 窗,傅里叶变化点数为256 个,窗口重叠数为傅里叶变化点数的一般为128 个,采样频率为60 min,功率谱分析结果如图1所示。

图1 2017年观测数据谱分析结果Fig.1 Spectral analysis result of 2017 observation data
功率谱表现出几个特征:周期介于2 ~48 h 内出现了几个明显的谱峰,其中周期在24 h 或12 h 左右的谱密度较高,12 h 左右的谱密度最高,略高于24 h 的谱密度,这说明该海域半日潮占优。周期在8 h、6 h 和4 h 左右也出现了谱峰,但峰值明显低于12 h和24 h。
3.2 1 a潮位资料分析主要分潮振幅
本文首先对老虎滩验潮站369 d 的逐时潮位进行调和分析,筛选分析出67 个分潮,其中包含42 个天文分潮和25个浅水分潮。
图2 为调和分析得到的各分潮的频谱图,振幅大于95%显著线的为主要分潮,振幅小于显著线的则为次要分潮。结果表明,67个分潮中有52个分潮为主要分潮(蓝色),其中包括31 个天文分潮和21个浅水分潮,其他15 个则为不显著的次要分潮(红色)。
图2 中频率大于0.1 cph(cycle per hour)的高频分潮多为浅水分潮,多数低频分潮集中在0.08 cph(半日潮)和0.04 cph(日潮),这与水位功率谱分析的结果基本一致。1 a 周期分潮SA 和0.5 a 周期分潮SSA也是显著分潮,但周期为1 M和0.5 M的低频分潮并不显著。老虎滩潮汐振幅最大的前6个主要分潮(按振幅大小)分别为M2、S2、K1、SA、N2和O1。
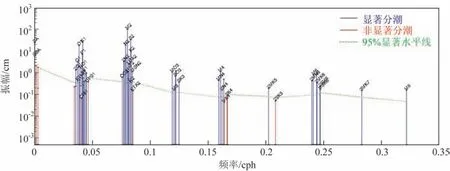
图2 老虎滩1 a潮位资料潮汐频谱图Fig.2 Frequency spectrum of one-year tidal level data in Laohutan station
潮汐类型以全日分潮和半日分潮的振幅比为量化指标,我国采用以下公式计算[7]:
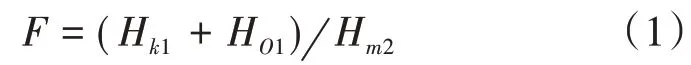
式中,H表示分潮的振幅。我国判断潮汐类型的标准为:当0 <F≤0.5时,为规则半日潮;当0.5 <F≤2.0时,为不规则半日潮;当2.0 <F≤4.0 时,为不规则全日潮;当F>4时,为规则全日潮。经计算,老虎滩潮汐类型值为0.429 1,为规则半日潮海区。
3.3 3 M潮位资料分析主要分潮振幅
对于3 M的短期潮位资料,由于时间长度较短,部分分潮无法分辩,调和分析得出的分潮数会有很大不同。图3是对老虎滩验潮站短期观测潮位数据的频谱图,未引入差比关系计算随从分潮,也未添加任何浅水分潮。对于短期观测资料,共分析出35个分潮,其中包括19 个天文分潮和16 个浅水分潮,比1 a期潮位资料获得的67个分潮数少32个。
由图3 可以看出,短期潮位资料调和分析出的频谱图与长期潮位资料的频谱图分布较类似,半日潮和全日潮振幅较大,M2、S2、O1和K14 个分潮最大,振幅基本一致,这也说明利用长期或短期资料均能调和出其主要分潮;主要的差异在于分离出的分潮数,短期资料分离出的高于绿色显著线的分潮有24 个,包括11 个天文分潮和13 个浅水分潮。长周期分潮(比如1 a周期的SA和0.5 a周期的SSA)均未见,得出的周期为1 M和0.5 M的低频分潮不显著。
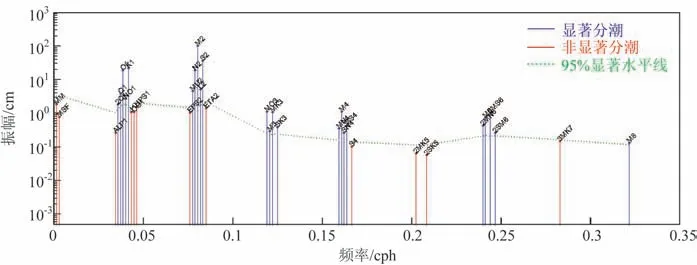
图3 老虎滩3 M潮位资料潮汐频谱图(未引入差比关系和浅水分潮)Fig.3 Frequency spectrum of three-months tidal level data in Laohutan station(difference ratio and shallow-water tidal component are not introduced)
对小于1 a的潮位资料进行分析时,需要通过引入差比关系分析随从分潮,还可根据需要添加浅水分潮。这里根据给出的主分潮和随从分潮的差比关系推算出3 M 分潮中所缺的半日和全日随从分潮,如随从分潮σ1、P1、π1、K2、2N2和λ2可分别由主分潮O1、K1、K1、S2、N2和M2推出,添加的浅水分潮有SO3、MK4、SK4、2MK6、MSK6和MSN2等。
图4 是引入差比关系和浅水分潮的分析结果。与未引入差比关系的结果相比,引入差比关系后分析出的分潮增加了14 个天文分潮和8 个浅水分潮,其中信噪比大于1的显著分潮有9个(见图4标注的分潮),其它的13 个都是非显著的次要分潮。在9个新增的显著分潮中有3个浅水分潮,其中MSN2分潮的频率是0.085 cph,是半日潮性质,SO3和2MK6是高频浅水分潮。9 个分潮中,振幅最大最显著的分潮是半日潮K2,其次为全日潮P1,浅水分潮SO3的振幅虽然不是很大,但是其信噪比仅次于K2和P1。

图4 老虎滩3 M潮位资料潮汐频谱图(引入差比关系和浅水分潮)Fig.4 Frequency spectrum of three-months tidal level data in Laohutan station(difference ratio and shallow-water tidal component are introduced)
综上所述,1 a和3 M 潮位观测资料的调和分析结果有较大区别,3 M 潮位资料得出的分潮数显然比1 a资料得出的分潮数要少很多,虽然可以通过差比关系推算出其他随从分潮的调和常数,但是尚有部分主分潮无法从3 M 潮位数据中分析出来。因此,为了保证预报的准确性,本文利用1 a 潮位数据分析出的调和常数进行2019年的天文潮预报,并与老虎滩验潮站的实测潮位数据和天文潮数据(潮汐表数据)进行对比分析。
3.4 基于T_TIDE 调和分析的潮汐预报结果验证评估
图5a 是T_TIDE 得出的2019 年老虎滩天文潮预报值与验潮站实测值的对比。图5b 是2019 年国家海洋信息中心发布的老虎滩潮汐预报值与验潮站实测值的对比图。图5c 是潮汐表预报值与T_TIDE 预报值的对比。为了更清晰地进行对比,我们选取了800 h的结果对比绘图,并统一其起算面。
从对比结果来看,观测潮位(实测值)中除了含有天文潮外,还包括由温带气旋和热带气旋等引起的余水位。由图5a 可以看出,观测水位与T_TIDE预报的天文潮在某些时间差异较大,在第700 h 左右能明显看出较大的余水位。同样的现象也出现在潮汐结果上(见图5b)。利用T_TIDE 预报的天文潮与潮汐表的预测结果接近,差异较小,最大差值仅17.6 cm(见图5c)。
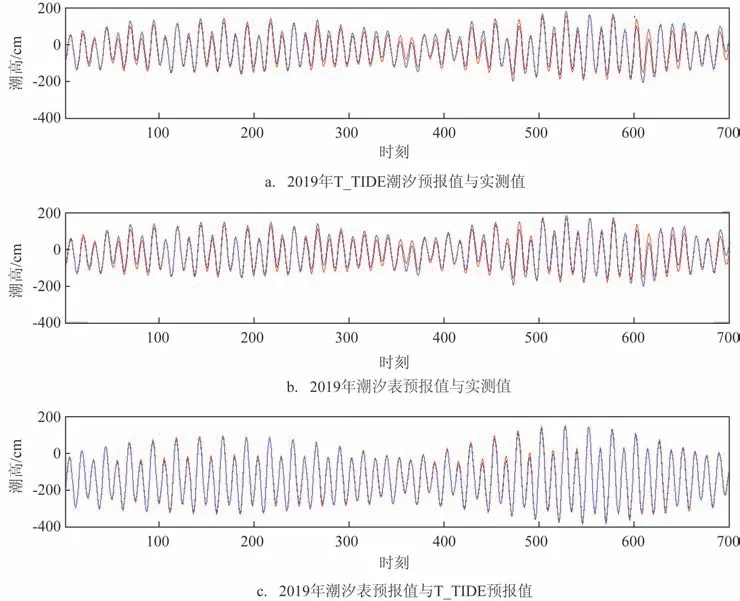
图5 T_TIDE预报值、实测值及潮汐表预报值两两对比图Fig.5 Comparison diagrams of T_TIDE predicted value,measured value and predicted value by tidal table
为了更清晰地看出本文的分析结果与实际水位的差异,我们选取了2019 年全年的数据进行对比。图6 是2019 年老虎滩T_TIDE 预报潮高与实测潮高的散点图,其中横轴为验潮站的实测值,纵轴是T_TIDE 的预报结果,红线代表预报值与实测值相等。图7 是预报值与实测值的分位数图,横轴为实测分位数,纵轴为预报分位数,图中的红线是两者完全重合的理论线。由两图可见,在整个潮高变动区间内,尤其是潮高在100~400 cm 以内时,两者总体符合良好,而在实测值小于100 cm 和大于400 cm时,T_TIDE的预报结果偏高。
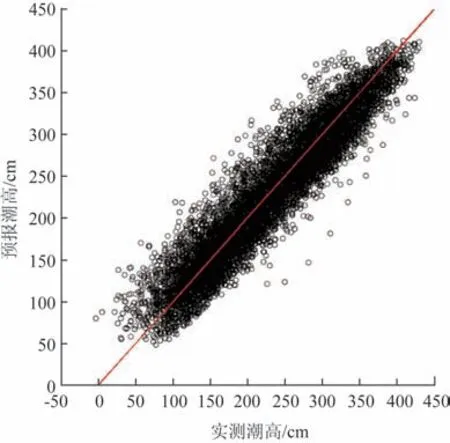
图6 老虎滩2019年T_TIDE预报潮高与实测潮高散点图Fig.6 Scatter diagram of T_TIDE prediction and observation of year 2019 in Laohutan station
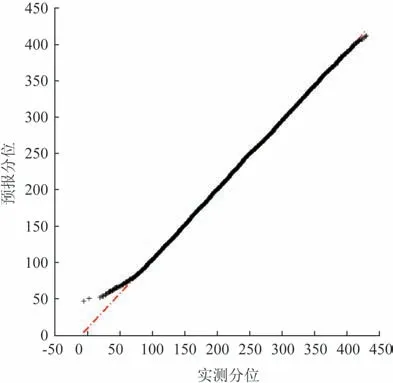
图7 老虎滩2019年T_TIDE预报潮高与实测潮高分位Fig.7 Quantile of T_TIDE prediction and observation of year 2019 in Laohutan station
平均绝对误差(Mean Absolute Error,MAE)和均方根误差(Root Mean Squared Error,RMSE)是衡量变量精度的两个常用指标,可以用来衡量预报值与观测值之间的偏差。两者定义分别如下:

式中,H表示实测值,h表示预报值,这两个值均会随着样本个数n的增大而增大。当预报值和实测值偏离不大时,这两个值的比值接近于1。如果预报值中有偏离实测值很大的值存在,那么RMSE 会将偏离的误差二次平方放大,最终导致RMSE 的值比MAE偏大。
表1是根据式(2)和(3)分别计算的潮汐表预报值及T_TIDE预报值的MAE和RMSE。从表中能看出MAE和RMSE相差不大,两者的MAE∶RMSE都接近于1,说明潮汐表和T_TIDE 预报值中没有异常值。T_TIDE 的MAE 和RMSE 比潮汐表的偏小,表明T_TIDE 预报值对实测值的累计误差少,T_TIDE 的预报结果略优于潮汐表的预报结果。
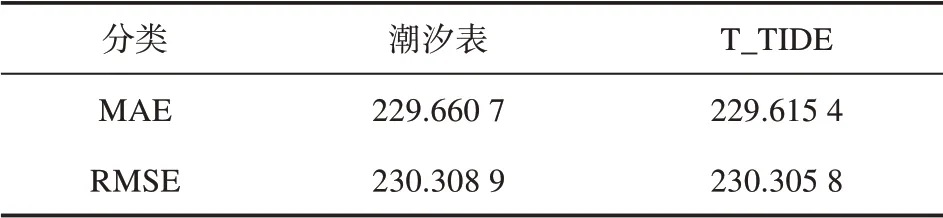
表1 潮汐表与T_TIDE对实测值的精度指标Tab.1 Precision indexes of Tide Table and T_TIDE predictions to observation
为了进一步对比T_TIDE 和潮汐表的预报效果,将两者预报的潮差最大值、最小值和实测值进行对比(见表2)。从潮差结果也可以发现T_TIDE的预报效果略好。

表2 潮汐表、T_TIDE及实测值潮差对比(单位:cm)Tab.2 Tidal range comparison between tide table,T_TIDE and observation(unit:cm)
3.5 T_TIDE预报余水位检验
实际观测到的潮位可写为:

式中,H为实测潮位;为多个调和分潮潮位叠加值;r为余水位或噪声,它包括由气象等因素引起的不规则扰动、观测中存在的误差、数据处理中的误差、截断误差和被忽略的分潮等,有时也简单地称为观测误差。如果余水位r的概率呈现正态分布,则表明所得的结果更为可靠[6]。
图8是T_TIDE预报的余水位的频率分布,横轴代表余水位(实测-预报)的预测残差,纵轴表示各组余水位数据发生的频率。由图8 可以看出,T_TIDE 潮高预报的余水位服从正态分布,即高斯分布,这与Powlowicz等[15]的结论一致。
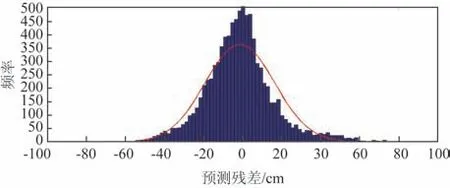
图8 老虎滩余水位(实测-预报)频率分布Fig.8 Frequency distribution of residual water level(measured-forecast)in Laohutan station
表3 给出了余水位的均值、方差和95%的置信区间。余水位均值近似为0,可以认为是服从均值为0 的正态分布,方差和区间长度小说明预报的准确度高。
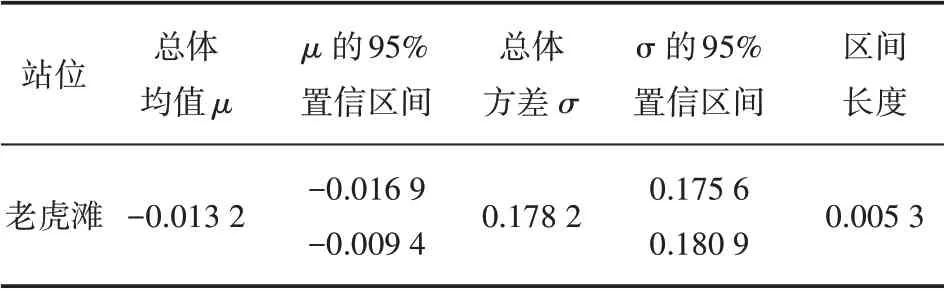
表3 老虎滩余水位统计值Tab.3 Statistical values of residual water level in Laohutan station
4 结论
本文利用T_TIDE 工具箱对老虎滩验潮站1 a潮位资料和3 M 潮位资料进行调和分析。结论如下:
(1)相比3 M 潮位资料分析结果,1 a 潮位资料能分析出较多的天文分潮和浅水分潮。老虎滩潮汐振幅最大的前6 个主要分潮分别为M2、S2、K1、SA、N2和O1,潮汐类型属于规则半日潮。
(2)对3 M的潮位资料进行调和分析的结果与利用1 a资料调和分析得出的结果有很大不同,少于1 a 的潮汐资料不能分析出长周期的分潮以及一些主分潮,需要添加差比关系来计算随从分潮,并且添加必要的浅水分潮。
(3)进一步利用T_TIDE 将1 a 潮位资料计算出的调和分潮常数进行老虎滩2019年天文潮预报,预报残差符合正态分布,残差均值小于10-2m,置信区间长度小于10-2,且该预报结果与潮汐表潮汐预报值相差不大。
以上结论表明,调和分析工具箱T_TIDE 对资料长度大于1 a的潮汐资料有较好的分析结果,并能较好地进行潮汐预报。对于资料长度太短的潮汐资料,其不能分析出长周期分潮,以致影响后续潮汐预报。

