基于深度学习的智能驾驶车辆路径仿真研究

何倩，仝武宁

（陕西中医药大学 计算机实验中心，咸阳712000）

信息融合模型在智能驾驶领域有重要意义，可基于这种技术融合环境信息并作出判断，为路径规划提供支持，做出相应的车辆路径规划，进而控制车辆的自动驾驶［1-2］.在智能驾驶领域需要重点解决的问题之一就是路径规划问题，路径规划可基于范围的不同进行划分，而分为全局和局部路径规划［3］.前者含义为在一定地图支持下，确定出起点到终点间的最适宜路线，后者则是融合传感器采集的环境信息同时根据全局规划信息，确定出满足要求的局部路径.无论是车辆到达预定目的地，还是车辆应对紧急情况必须具备的应急决策能力，都需要一种具有较强学习能力的人工智能方法来达到相应的目的，强化学习（Reinforcement Learning，RL）就是这样一种方法［4-5］.然而，传统的强化学习在复杂多样的环境中存在着Q 值估计过高、无法解决连续动作任务、收敛速度慢甚至难以收敛等问题［6］.深度学习（Deep Learning，DL）的研究可以有效地弥补强化学习的不足.Google 公司在研究过程中提出深度强化学习（Deep Reinforcement Learning，DRL）方法.与深度学习的结合不仅可以将强化学习应用到高维空间，而且还带来端到端的优化，使得强化学习的应用范围得到延伸［7］.其中，深度强化学习中的DDPG 算法，将Actor-Critic 框架和DQN 算法进行融合.DDPG 不仅吸收Actor-Critic 中战略梯度单步更新的特点，而且吸收了DQN 算法中Q 值估计技巧.DDPG 最大的优势在于可以更有效地学习连续动作.在交通领域中，截止到目前为止DDPG 算法的应用还较少.

1 相关工作

近年来，随着深度强化学习的兴起，越来越多的国内外学者开始研究它在解决组合优化问题中的应用，其中路径规划问题是典型的组合优化问题.王万良等［8］为解决多配送中心车辆路径规划问题，以最小化总车辆路径距离为目标，提出了一种基于多智能体深度强化学习的求解模型.上述方法均采用编码器-解码器结构，一些学者采用图神经网络模型进行求解.例如，LI等［9］使用图卷积网络来估计图中每个顶点属于最优解的概率，并通过树搜索解决多个组合优化问题；NOWAK 等［10］使用图卷积网络生成选择图形每条边的概率，并使用波次搜索获得TSP的最优解.WU 等［11］结合深度强化学习和启发式两种方法，采用DRL 学习车辆路径问题的主动规则，该方法的实验结果优于端对端的DRL 求解出的最优解.余伶俐等［12］针对智能车路径规划领域环境感知相关的缺陷进行分析，引入基于蒙特卡罗深度策略梯度学习（Monte Carlo Prediction Deep Deterministic Policy Gradient，MCPDDPG）的路径规划技术，建立起融合环境感知和行为决策智能规划模型，实现实时决策和规划，并输出连续的车辆控制序列.

2016年，DeepMind团队首次建立起深度确定性策略梯度（DDPG）算法，且对其性能做了仿真分析，结果发现明显高于传统DPG 模型.DDPG 算法结合了DQN 算法的优势，且进行适当的改进而提高了其学习效率，所得的路径规划结果更优.PHANITEJA等［13］在对机器人轨迹训练时应用了DDPG 算法，且对其性能做了仿真分析；DO 等［14］在研究过程中基于DDPG 算法建立起机器人自动化浇注系统，在运行过程中可实现避障和防洒落功能，在此基础上将液体倒入指定高度.黄志清等［15］通过TROCS 平台的不同自动驾驶汽车赛道对DDPG 算法进行训练，并将训练结果与DQN 算法进行对比，结果表明DDPG算法在控制精度以及泛化性方面具有更好的效果.DDPG 算法的特征表现为对连续控制问题可高效的处理，而弊端则表现为训练难度大，需要大量的训练样本，同时初期输出结果的可靠性差.

2 ERDDPG算法的设计

2.1 Q-learning和DQN

Q-learning 是传统的强化学习方法，DQN 是Qlearning和神经网络融合形成的，两者在处理过程中都基于环境信息，利用值函数进行分析确定出最佳战略.在数学量化分析时可基于如下表达式描述出Q-learning的动作值函数：

其中，s"表示在状态s时选择动作a后跳转到的下一个状态，α是学习率，λ是未来状态的奖励值换算到当前时刻状态的衰减，即表示未来Q 值对当前状态的带有衰减的影响，表示下一时刻状态s"当中最大的Q值，其具体流程如图1所示：

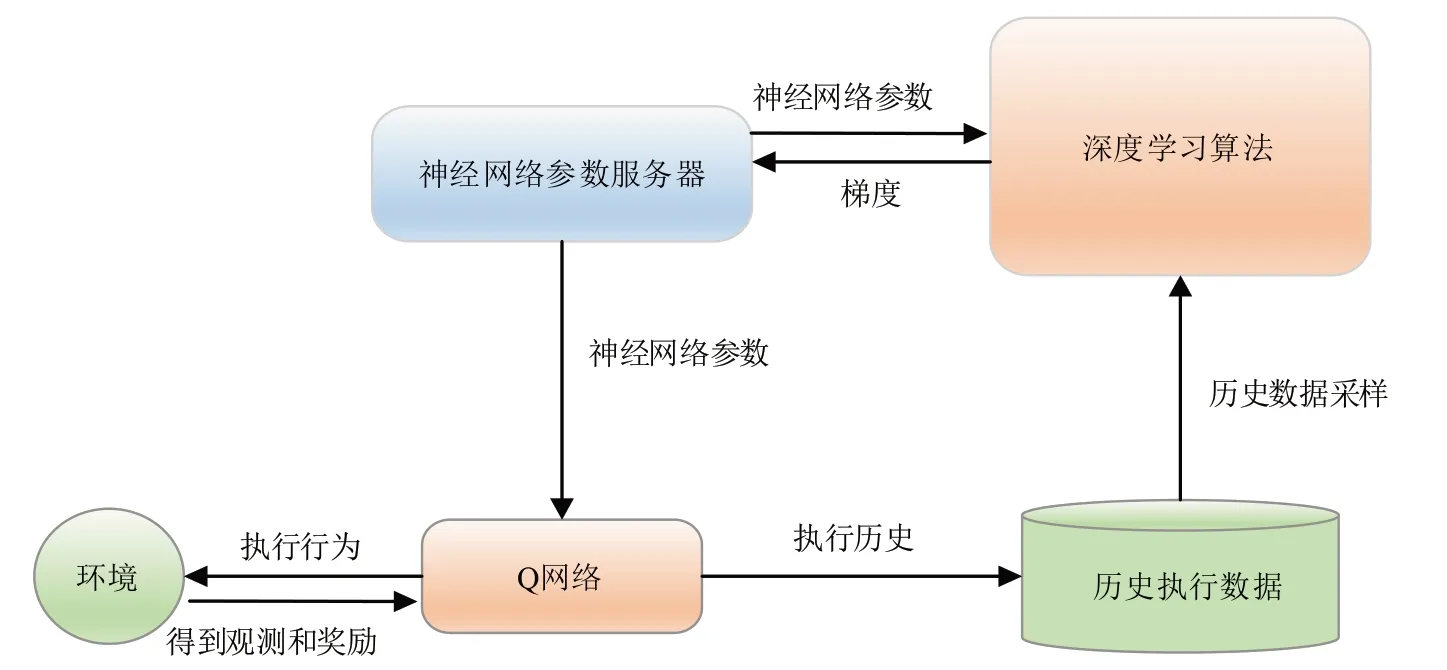
图1 Q-learning算法流程图Fig.1 Q-learning algorithm flow chart

DQN在Q-learming基础上主要做了以下修改：

（1） 通过DCNN网络逼近值函数.

对比分析可知其中的值函数和每层网络的权重保持对应，记作θ，值函数描述为Q(s，a；θ).这种条件下对DQN 中的值函数进行更新过程中，主要是对参数θ进行更新，在网络确定条件下，设置的函数就是θ.

（2） 在强化学习时应用经验回放训练方法.

采用经验回放的主要目的：一方面，深度神经网络在处理过程中需要输入独立同分布的数据，而基于强化学习方法搜集的数据间存在一定关联性，这样直接通过这些数据来训练网络，则不满足应用要求，容易导致不稳定的问题，为此引入了经验回放方法来进行数据的独立化处理.

（3） 设置了目标网络处理TD偏差.

神经网络在逼近值函数过程中主要是对其中的参数θ进行更新，对应的更新策略表示如下：

DQN的工作流程如图2所示.

图2 DQN算法工作流程图Fig.2 DQN algorithm workflow

2.2 Actor-Critic框架

Policy Gradient 模型在处理过程中，为实现最大化目标，调节参数θ沿目标函数梯度方向不断变化，设置的目标函数也即奖励的期望值，可通过如下表达式描述：

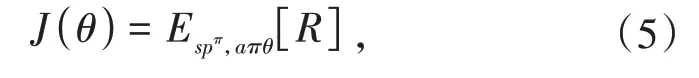
在参数更新过程中，应用了梯度下降法，对应的表达式如下：

其中，πθ(a|s)为在状态s下采取动作a的发生概率；pμ为状态分布；Qπ(s，a)为策略π下状态s采取动作a一直到回合结束的总回报，Qπ(s，a)越大，梯度下降的越快，选择该动作的机率就越大.简单来说，当策略πθ(a|s)沿梯度方向更新参数时，Q 函数会作为一个“监督者”来把控更新的幅度.

基于策略的算法由于是沿梯度方向更新，往往会偏离预期奖励，产生很高的方差，可以通过加入基线的方法缓解，即：

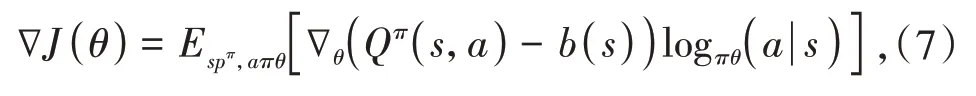
其中，b（s）为基线函数，当b(s)=Ea(Qπ(s，a))=V(s)（状态值函数）时，方差最小.

在参数更新过程中，如果融合了这种算法和基于值的算法，通过TD模式进行更新，这种条件下更新模式也出现明显的变化，从回合更新变成了单步更新，对应的算法也就是“Critic”，总体上分析可知Actor-Critic算法在处理过程中对应的流程如图3所示.

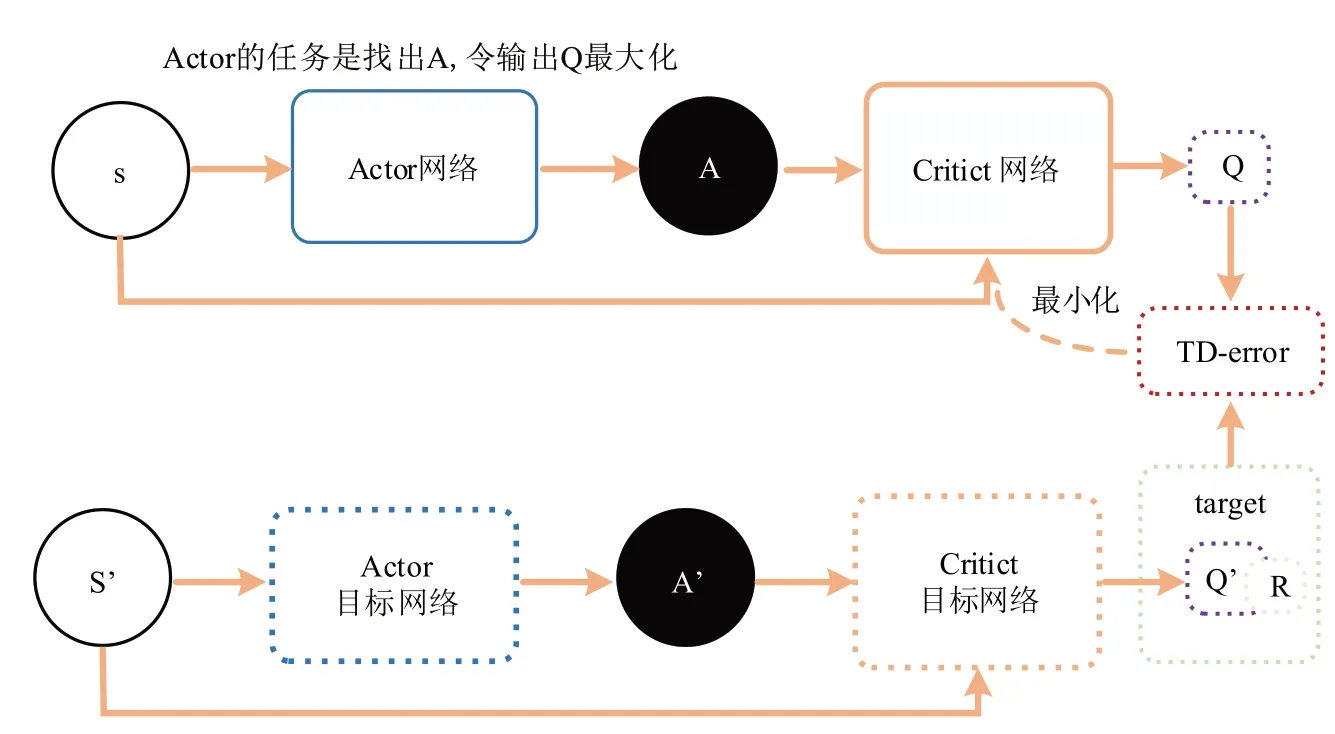
图3 Actor-Critic框架算法的基本流程图Fig.3 Basic flow chart of Actor-Critic framework algorithm

2.3 ERDDPG算法流程

ERDDPG 算法是Actor-Critic 框架与DQN 算法的融合.ERDDPG 在处理过程中为提高学习效率而引入了经验回放方法和双网络结构.Actor 网络可给出具体的动作，在网络学习过程中主要是在连续的动作空间下实施，因而对应的效率更高.这两个框架下都设置了目标网络和估计网络，对网络进行训练过程中，单纯的更新估计网络的参数，前一种网络中的参数定期直接复制，这种模式下简化了网络训练的难度.Critic 学习过程中应用了损失函数方法，对应的表达式如下：

其中，Q*(s，a|θ)基于估计网络确定出，a是传过来的动作学习，y是Q 值，这种策略下计算机目标Q 值过程中，应用了Actor 传输的a".在对估计网络进行训练过程中应用了目标Q 值和估计Q 值的平方损失，这两个值的获取方法不一致，前者主要是通过奖励γ，下一刻的动作a"，输入网络中确定出Q 值进行折扣后加和得到；后者则基于当前状态s和动作a输入Critic 中进行估计确定出.Actor 网络在进行参数更新过程中应用到策略μθ：S →A，且结合如下的表达式：

由于这个定理依赖于∇aQμ(s，a)，因而需要满足一定的条件约束，也就是动作空间A连续.在处理过程中对同一个状态，输出与此相关的动作a1和a2，接着进行估计分析确定出反馈的Q1和Q2值，判断如发现Q1＞Q2，这种条件下执行动作a1对应的获益更大.策略梯度方法处理时的思路为：提高a1的概率，而下调a2的概率，这样使得Q值更大.ERDDPG 算法流程如图4 所示，输入状态为(d1，…d9，v，δm)，输出动作为δ.此算法的优点是需采样的数据少，算法效率高.

图4 ERDDPG算法流程图Fig.4 ERDDPG algorithm flow chart

3 仿真实验与分析

本文的ERDDPG 模型中的超参数如下：Actor与Critic的学习率均为10－4，通过Adam 进行优化.更新率为0.001，经验回放池为104，初始最大方差varmax=2，最小方差varmax= 0.01，衰减率为10－4.分别进行0o、30o、-30o航向角的车道保持实验.图5显示的是0o航向角的车道保持实验结果.图6 显示的是30o航向角的车道保持实验结果.图7 显示的是-30o航向角的车道保持实验结果.

图5 0o航向角的车道保持实验结果Fig.5 Experimental results of lane keeping at 0°heading angle

图6 30o航向角的车道保持实验结果Fig.6 Experimental results of lane keeping at 30°heading angle

图7 -30o航向角的车道保持实验结果Fig.7 Experimental results of lane keeping at-30°heading angle

在轨迹跟随过程中，车辆的运动状态良好，各特征量平稳，车辆在运行过程中各方向的加速度、航向角和转角参数都保持平稳变化，各量值和动力参数也满足相关约束要求.智能驾驶车辆车速为12 m/s，从中间车道近中心位置分别以0°航向角、30°航向角和-30°航向角出发，适当的调节方向盘控制序列而实现车道保持控制目标.车辆在初始位置有一定偏差，通过算法适当的微调后保持车道平稳，方向盘转角趋近于0°，进行仿真分析发现稳定后对应的车辆横向偏差均值为0.05 cm.ERDDPG 模型在处理过程中对应的流程为，先将环境信息和agent 交互，将所得数据保存后形成经验池，通过这些经验信息不断的学习，并更新参数，采用优先经验回放机制，针对不同的经验数据进行分析设置不同的优先级，在此基础上更优化的选择样本.之后，本文对Dijkstra 算法、人工势场法以及ERDDPG 算法进行对比实验.其中智能驾驶车辆在场景中根据规划结果仿真行驶，对比规划效果.Dijkstra 算法在确定转角控制序列时应用了预瞄窗方法，而人工势场法在处理时直接输出这种序列.车辆行驶过程中，120 ms 内保持同一偏转角，此后则重新规划.Z形换道场景的横向误差对比实验如图8所示.

根据图8 所示，对比Z 形换道场景，智能驾驶车辆从上车道换人中间车道.实验结果验证ERDDPG算法在弧形直道行驶时具有良好性能且在控制动作的连续性上更优，这3 种规划方法均能顺利完成换道动作，但Dijkstra算法完成换道所需时间较长且完成时与中间车道的横向误差为35 cm，人工势场法的横向偏差为22 cm，需经过短时间调整进入低误差的车道保持状态，ERDDPG 方法换道动作干脆，横向偏差不超过12 cm.总体上分析可知强化学习的主要目的在于最大化累计奖励值，从而确定出符合要求的最优策略，根据相关奖励值设定经验数据的权重，奖励值大条件下被采样的可能性更高.在参数更新过程中立即奖励值不会改变，因而可以确保这种回放模式的稳定性高，对应的样本更可靠.

图8 Z形换道场景横向误差的对比Fig.8 Comparison of horizontal error of Z-shaped lane changing scene

4 结语

本文对智能驾驶领域深度强化学习相关的原理和应用问题进行研究，在面对高维状态空间以及动作空间的问题时，对DDPG 算法进行分析，所得结果表明DDPG 算法训练过程中，容易出现无效训练和高质量经验样本没有被充分利用的问题.因此，本文采用一种改进的经验回放机制ERDDPG 算法应用于智能驾驶路径规划.仿真实验证明了本文算法在运行过程中可输出确定性的动作策略，连续控制模式下算法的性能良好，可满足此领域的智能路径规划性能要求.在深度强化学习中策略函数和值函数都是由深度神经网络表示的，这种模式下出错后难以确定原因，所以模型的可解释性是未来需要改进的重要研究方向.