基于GEO-RVM模型的枯水期月径流预报研究

张亚杰，崔东文

(1.云南省玉溪市易门县水利局，云南 玉溪 651100；2.云南省文山州水务局，云南 文山 663000)

枯水期江河流量小，水资源供需矛盾突出。提高枯水期月径流预报精度对于缓解生产生活用水供需矛盾具有重要意义。目前用于月径流预报的方法有传统人工神经网络法[1-2]、支持向量机法[3-5]、长短时记忆神经网络法[6]、组合预测法等[7]。在国内月径流相关预报研究中，由于支持向量机(support vector machines，SVM)具有结构简单、全局理论最优、克服维数灾等优点，无疑在枯水期月径流预报研究中应用最为广泛。相关向量机(relevance vector machine，RVM)是Micnacl E Tipping[8]于2000年提出的一种与SVM(Support Vector Machine)类似的稀疏概率模型，已在径流预报相关研究中得到应用。与SVM相比，RVM具有以下优势：①同SVM相比，RVM极大地减少核函数的计算量，克服了所选核函数必须满足Mercer条件的缺点；②RVM基于贝叶斯框架构建学习机，相关向量数目远少于 SVM中的支持向量数目，模型相对简洁；③RVM自动赋值惩罚因子，不存在因惩罚因子设置不当带来的过学习等问题；④与SVM相比，RVM更稀疏，预报时更短，泛化能力更优。在径流预报中，虽然RVM具有较好预报性能，但RVM“超参数α”和“核函数宽度因子d” 2个关键参数的科学选取对提高RVM预报精度十分关键。目前除传统优化方法，如粒子群优化算法(PSO)[9-10]、蝙蝠算法(BA)等[11]用于RVM关键参数优化外，一些新型群体智能仿生算法(SIBA)，如鲸鱼优化算法(WOA)[12]、鸡群优化(CSO)算法[13]、海鸥优化算法(SOA)[14]、蝗虫优化算法(GOA)等[8]已偿试用于RVM关键参数优化，并取得较好的优化应用效果。

为提高枯水期月径流预报精度，拓展群体智能仿生算法优化RVM关键参数的应用范畴，研究提出一种基于金雕优化(Golden Eagle Optimization，GEO)算法与RVM相融合的径流预测方法。基于云南省某水文站67 a的径流资料，以枯水期11月、12月和次年1—4月月径流预报为例，选取预报月之前具有较好相关性的月径流作为预报影响因子，通过主成分分析(PCA)对影响因子进行降维处理，利用GEO算法优化RVM核宽度因子和超参数，建立GEO-RVM月径流预报模型，并构建GEO-SVM模型作对比，通过实例验证GEO-RVM模型用于枯水期月径流预报的可行性。

1 GEO-RVM预测模型

1.1 金雕优化(GEO)算法

GEO算法是Abdolkarim Mohammadi-Balani等于2020年基于金雕狩猎行为而出的一种新颖群智能元启发式算法。该算法通过模拟金雕在狩猎过程中智能调整搜索策略和攻击策略来捕食猎物，并达到求解待优化问题的目的。GEO算法基于以下假设：①金雕沿着螺旋轨迹进行搜索猎物，并沿着直线路径进行攻击；②金雕在狩猎初期表现出更大的搜索倾向，在狩猎后期表现出更大攻击倾向；③金雕在飞行的每个时刻都保持搜索和攻击倾向；④金雕同时搜索其他金雕锁定的猎物信息[15]。

与其他启发式算法相比，GEO算法原理简洁、实现简单、设置参数少，而且具有较好的寻优精度和全局搜索能力。GEO算法数学描述简述如下[15]。

a)猎物锁定。GEO算法中，每只金雕都记住它迄今为止所探测过的最佳猎物位置，且同时具有攻击猎物和巡航搜索猎物的倾向。每次迭代中，金雕i随机选择另一只金雕f的猎物，并绕着金雕f迄今为止所获得的最佳位置进行盘旋，金雕i也可以选择盘旋自己的目标猎物。

b)记忆更新。在GEO中，猎物被模拟为金雕群迄今为止发现的最佳解决方案(待优化问题最佳解)，每只金雕都能记住迄今为止找到的最佳解决方案。在迭代过程中，每只金雕从金雕群体的记忆中选择一个目标猎物，然后计算每只金鹰的攻击向量和巡航向量，如果新位置优于记忆中的先前位置，则将更新记忆。

c)攻击策略(开发阶段)。攻击策略可以通过一个向量来模拟，该向量从金雕当前位置开始，到金雕记忆中猎物位置结束。由于攻击向量将金雕种群引向最佳猎物位置，因此突出了GEO的开发阶段。金雕i的攻击向量可以通过式(1)计算。

(1)

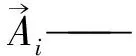
d)巡航策略(勘探阶段)。GEO基于攻击向量计算巡航向量，巡航向量是圆的切线向量，垂直于攻击向量。巡航被认为是金雕相对于猎物的线性速度。GEO算法利用式(2)表示n维空间中超平面方程的标量形式。

(2)

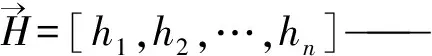
(3)

e)位置更新。GEO算法中将金雕i第t次迭代步长向量Δxi定义为：

(4)

则第t+1次迭代金雕位置更新如下：

(5)

式中xt+1——第t+1次迭代金雕位置；xt——第t次迭代金雕位置；Δxi——步长向量。

f)勘探到开发过渡。GEO使用pa和pc从勘探转向开采。该算法从低pa和高pc开始，随着迭代的进行，pa逐渐增加而pc逐渐减小。pa、pc数学描述如下：

(6)

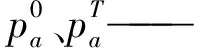
1.2 相关向量机(RVM)

(7)

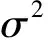
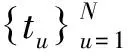
(8)

式中t=(t1，t2，…，tN)T；Φ——N×(N+1)的核函数矩阵。

(9)

式中α——N+1超参数向量。

基于贝叶斯公式，后验分布的权重描述为：

p(ω|t,α,σ2)=(2π)-(N+1)/2

(10)

式中μ=σ-2∑ΦTt；∑=(σ-2ΦTΦ+A)-1；A=diag(α0,α1,…,αN)。

为建立统一的超参数，p(t|α,σ2)定义如下：

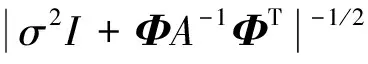
(11)

本文利用高斯径向基核函数(RBF)作为核函数，即：

(12)

式中d——核函数宽度因子。

1.3 预测模型的建立及实现步骤

步骤一基于实例实测径流资料，选取与预报月11、12月和次年1—4月具有较好相关性的月径流作为预报影响因子。参考文献[16]，采用PCA对预报影响因子进行降维处理，并合理划分训练及预报样本，利用GEO算法优化RVM超参数α和核函数宽度因子d，建立GEO-RVM径流预测模型，利用训练样本数据对GEO-RVM模型进行训练。

步骤二选用训练样本均方误差作为优化目标函数：

(13)

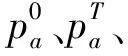
步骤四评估目标函数适应度值，选取并保存具有最佳适应度值的金雕位置x*。令当前迭代次数t=1。

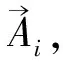
步骤六评估金雕新位置的适应度函数，如果当前金雕位置的适应度优于前代金雕位置的适应度，则保留当前金雕位置为最佳位置；否则保留前代金雕位置为最佳位置。

步骤七令t=t+1。判断t是否等于T，若是，输出最佳金雕位置x*，算法结束；否则重复步骤五至步骤七。

步骤八输出最佳金雕位置x*，x*即为RVM超参数α和核函数宽度因子d向量。

图1 GEO优化流程

2 实例分析

a)数据来源及相关性分析。该实例水文站系红河流域泸江水系盘龙河干流控制站，控制径流面积3 128 km2，为国家重要水文站和中央报汛站。本文以该水文站1952—2018年实测水文资料为研究对象，通过计算预报月11、12月，次年1—4月月径流与之前月月径流相关系数。经计算，11月月径流与同年8—10月月径流的相关系数分别为0.541、0.444、0.627；12月月径流与同年4—5、7—11月月径流的相关系数在0.330～0.764；次年1月月径流与上年1—4、7—12月月径流的相关系数在0.333～0.914；次年2月月径流与上年2—5、7—12月和次年1月月径流的相关系数在0.321～0.945；次年3月月径流与上年1—2、4、8—12月和次年1—2月月径流的相关系数在0.328～0.871；次年4月月径流与上年4、8—12和次年1—3月月径流的相关系数在0.408～0.772。可见，各预报月与各相关影响因子之间均具有一定的相关性。

b)数据降维处理。由前分析可知，对于11月，预报影响因子3个，即3维，维度较低，无需进行降维处理；对于12月、次年1—4月，预报影响因子分别为7个(7维)、10个(10维)、11个(11维)、10个(10维)、9个(9维)，可采用PCA进行数据降维，以使数据样本简洁且更具代表性。本文参考文献[15]，利用SPSS软件对实例数据进行PCA降维处理，经处理，12月、次年1月前4个特征值累计贡献率分别为85.34%、87.49%，次年2月前5个特征值累计贡献率为89.20%，次年3月、次年4月前3个特征值累计贡献率分别为85.43%、85.38%。根据累计贡献率大于85%的原则，分别选取前4个(4维)、4个(4维)、5个(5维)、3个(3维)、3个(3维)变量代替原7个(7维)、10个(10维)、11个(11维)、10个(10维)、9个(9维)变量，并选取前60组数据作为训练样本，后6组数据作为预报样本。主成分分析结果见表1，降维数据及原始数据限于篇幅从略。

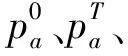
d)预测及对比分析。利用所构建的GEO-RVM、GEO-SVM模型对实例预报月11、12月，次年1—4月月径流进行训练及预报，并利用绝对平均相对误差MRE、平均绝对误差MAE、决定系数R2对2种模型性能进行评价。训练-预报相对误差见图2—7，预测结果见表2。

表1 枯水期预报月主成分分析结果

图2 11月月径流拟合-预报相对误差

图3 12月月径流拟合-预报相对误差

图4 次年1月月径流拟合-预报相对误差

图5 次年2月月径流拟合-预报相对误差

图6 次年3月月径流拟合-预报相对误差

图7 次年4月月径流拟合-预报相对误差

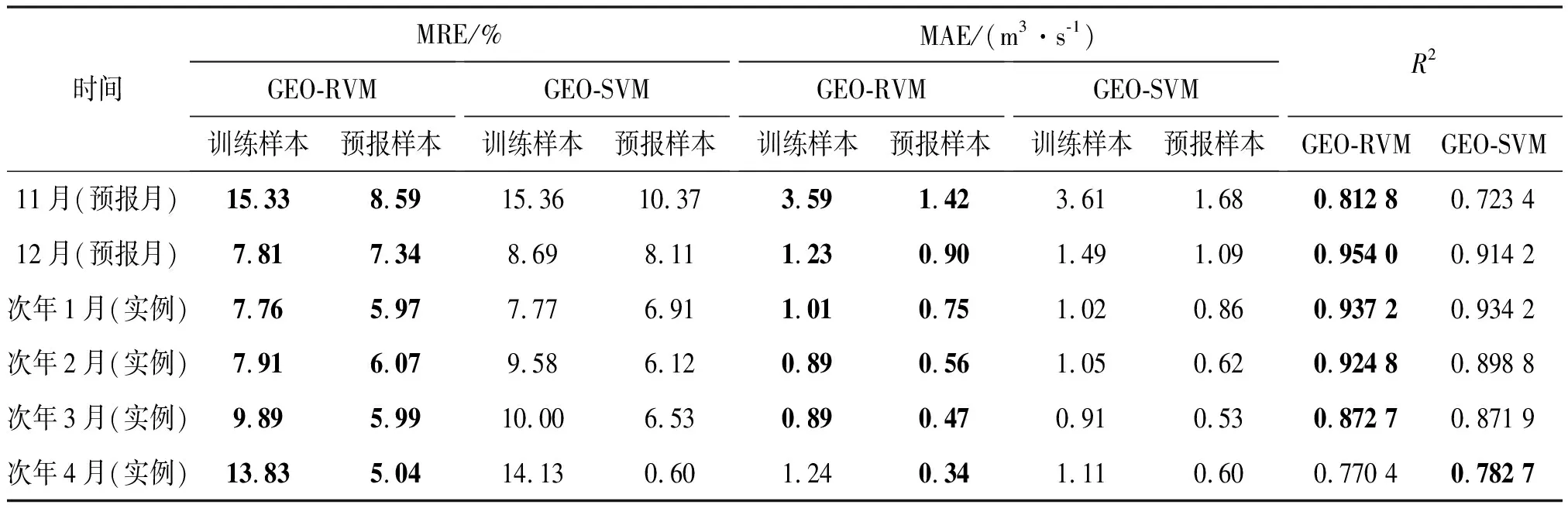
表2 枯水期月径流预报结果及其对比

依据表2及图2—7可以得出以下结论。

a)GEO-RVM模型对实例预报月11、12月，次年1—4月月径流预报的绝对平均相对误差MRE分别为8.59%、7.34%、5.97%、6.07%、5.99%、5.04%，平均绝对误差MAE分别为1.42、0.90、0.75、0.56、0.47、0.34 m3/s，预报精度均优于GEO-SVM模型，表明GEO-RVM模型具有较好的预报精度和泛化能力；同时也表明GEO算法能有效优化RVM超参数和核函数宽度因子，GEO-RVM模型用于枯水期月径流预报是可行的。

b)从决定系数R2来看，除次年4月外，GEO-RVM模型对枯水期预报月11、12月，次年1—3月拟合-预报的决定系数R2均大于GEO-SVM模型，表明GEO-RVM模型拟合-预报的整体效果要优于GEO-SVM模型。其中，枯水期12月、次年1年、次年2月拟合-预报的决定系数R2均大于0.92，拟合-预报效果优于其他月份。从图1—6也可以看出，GEO-RVM模型对枯水期12月、次年1年、次年2月拟合-预报效果更优，更接近实测值。

c)GEO-RVM模型对实例预报月11、12月，次年1—4月月径流预报的相对误差分别在-12.64%～14.66%、-9.58%～14.01%、-0.69%～13.94%、-8.43%～11.62%、-11.99%～7.66%、-13.40%～5.32%，相对误差均小于实测值的20%，达到水文预报甲等精度等级。

3 结论

介绍一种新型群体智能仿生算法——金雕优化(GEO)算法，利用GEO算法优化相关向量机(RVM)核宽度因子和超参数，建立GEO-RVM模型，并构建GEO-SVM模型作对比。通过云南省某水文站枯水期11、12月和次年1—4月月径流预报为例对GEO-RVM模型进行验证。结论如下。

a)GEO-RVM模型对实例枯水期月径流预报精度优于GEO-SVM模型，具有较好的预报精度和泛化能力。GEO算法能有效优化RVM超参数和核函数宽度因子，将GEO-SVM模型用于枯水期月径流预报是可行的。

b)GEO-RVM模型对实例枯水期12月、次年1年、次年2月的拟合-预报效果更优，更接近实测值。

c)本文介绍的GEO算法及提出的GEO-RVM模型可为径流预报及其他相关研究提供借鉴。