相关性分析-神经网络模型在宁夏用水量预测中的应用

窦 淼,李金燕,崔岚博，魏怡敏，苏荟琰，李超超

(宁夏大学土木与水利工程学院，宁夏 银川 750021)

水资源是社会发展中不可代替的自然资源也是不可或缺的经济资源。随着中国的现代化进程加快，对水资源的需求量越来越大，水资源供需矛盾日益突出[1]。尤其在中国干旱地区，水利设施落后，用水效率低下，这一系列问题严重制约了地方的发展。其中地处西北内陆的宁夏回族自治区是干旱区域的典型代表，也是中国最缺水的省份之一。该地区水资源人均占有量不足全国人均占有量平均值的1/2，水资源的严重匮乏已经成为制约该地区经济发展的主要因素。因此做好水资源规划工作对宁夏的社会经济发展有着举足轻重的意义，而用水量预测是水资源规划工作能顺利进行的前提和保障。由于在预测过程中存在影响因素考虑不全以及资料缺失等问题，用水量预测工作往往面临较大的困难。为了克服这些弊端，近些年国内学者在常规的系统分析法前均会对影响因子进行数学预处理，如桑慧茹等[2]在神经网络模型之前运用主成分分析法筛选影响因子；单义明等[3]在支持向量回归机模型之前加入灰色关联度筛选影响因子；李晓英等[4]采用主成分分析、遗传算法和神经网络三者结合的预测模型； Mahmut Fira等[5]将神经网络与模糊数学相结合预测区域耗水量；杨利纳等[6]在小区域内运用灰色关联、遗传算法和神经网络预测用水量，并引入预测区间覆盖率、预测区间平均宽带指标和综合评价指标检验预测结果。上述方法通过对用水量影响因子的筛选，一定程度上提高了模型的预测精度，但在处理影响因子时都忽略了影响因子和行业用水量的相关程度，直接分析总用水量和影响因子之间的关联性会打破各行业的影响因子数量的平衡性，且目前没有将相关性分析和MLP神经网络耦合的预测模型。故本文提出了将相关性分析法和MLP神经网络耦合的用水预测模型，分别提取对行业用水量影响较大的因子，与传统利用MLP神经网络直接预测总用水量的方法相比，该方法可以进一步提高预测的精确度，且可以掌握未来的各行业用水量的比例。

1 相关性分析和多层感知器神经网络耦合模型

1.1 相关性分析法

相关性分析法是统计学中的方法，它是对总体中具有联系的2个因素进行分析，描述客观事物相互间的密切程度并用相关的统计指标表示出来的一种数学方法[7-8]。相关性的表达通常有2种方法：皮尔逊相关性系数和斯皮尔曼相关性系数。在用水量预测中该方法可以用在建立神经网络模型之前，用来筛选对用水量影响较大的因子[9]。由于皮尔逊相关性系数是用来检验来自正态分布的总体，且要求试验数据之间的差值不能过大，对数据的要求较高。而用水量影响因子数据波动性较强，通常是随机分布，故选择斯皮尔曼相关性系数进行相关性计算。斯皮尔曼相关性系数又称斯皮尔曼秩相关系数，其具体计算步骤如下。

步骤一对2个变量x、y的数据分别进行排序，记录每个数据的秩次xi、yi。

步骤二计算每两个数据秩次的差值di(xi-yi)，再统计数据的个数n，将2个数值代入式(1)进行计算相关系数ρs。

(1)

步骤三对斯皮尔曼系数进行相关系数的显著性检验。对于小样本模型，可以直接通过查临界表，通过对比斯皮尔曼相关性系数和表中数值确定显著性。

判断两组数据是否具有相关性主要从相关性系数(ρs值)和显著性(P值)2个方面考虑，其中ρs的绝对值越接近1，表示相关性越强；P<0.01为相关性极显著，0.01≤P<0.05为相关性显著，P≥0.05为相关性不显著。在判断行业用水量影响因子和行业用水量之间的相关程度需根据具体情况采取不同标准。

1.2 MLP模型

MLP神经网络又称多层前馈神经网络[10]，是一种基于误差反向传播算法 (BP算法)训练的神经网络。误差反向传播算法是一种在用水预测中常见的训练神经网络的方法[11-12]，可以有效降低模型的计算误差。MLP神经网络模型在建立的过程中只需录入大量的数据行为无需用变量描述映射关系，故此模型具有很好的拟合能力[13]和抗外界干扰能力[14]。区域用水量存在很多不确定因素，但在用水量预测中利用MLP神经网络建模一定程度上可以克服这些不确定因素。MLP神经网络一般由输入层、输出层和若干隐藏层组成，典型的结构见图1。

图1 MLP结构示意

其中隐含层常用的激活函数是Sigmoid函数(S型函数)，假设输入值为x，函数的具体计算公式为：

(2)

式中α>0是常数，函数的取值范围是(0，1)，x为输入值。

另一种隐含层常用的激活函数是Tanh函数，具体计算公式为：

(3)

式中α、β>0是常数，函数取值范围(-1，1)。

以上2种函数都是建立MLP神经网络最常用的2种激活函数，Sigmoid函数优势在于求导容易且优化的数据比较稳定，而Tanh函数的优势是收敛速度更快。区域用水量预测的模型结构较为简单，相比较收敛速度更注重预测模型的稳定性和适用性，故本次建模的激活函数选择Sigmoid函数，在满足预测精度的前提下，为了简化模型结构在后续构建一个隐藏层的预测模型[15]。

在用水量预测模型中，为了提高输出值的稳定性，输出层的激活函数通常选择简单的恒等式函数，该函数是将隐藏层节点的数据按照训练出的权重比例进行加和，其表达式为：

(4)

式中Ri——隐含层第i个节点的数据；m——隐藏层节点个数；λ——权值；y——输出值。

1.3 耦合模型原理

借助相关性分析法对各个行业的用水量和其影响因子进行两两分析，计算相关性系数并依据相关标准提取和用水量相关性较强的因子，将提取出来的因子作为MLP神经网络的输入层，每个数据作为一个神经元节点。利用训练数集训练MLP模型，通过多次的训练，得出隐藏层的最优节点数，从而确定最佳的用水预测模型。

2 用水预测

2.1 研究区域概况

宁夏回族自治区处于中国西北内陆地区，常年干旱少雨，是中国水资源严重匮乏的地区之一。2020年全区用水量为66.54亿m3，水资源总量12.58亿m3，用水主要源自黄河水。在三大产业中，农业用水为58.64亿m3，占全区总用水量85%以上，工业用水和生活用水仅为4.19亿、3.71亿m3，但农业生产总值仅占全区生产总值的7.9%，工业生产总值占全区生产总值的33.9%。长期以来宁夏面临着农业用水效率低下的问题，常年采取大水漫灌的灌溉方法，加上种植结构不够合理，农业布局不够优化等因素，使单位农业产值用水量过大，远远高于全国平均水平。因此在宁夏用水预测的工作中，准确地预测农业用水量对整个自治区合理地用水规划将起到至关重要的作用。

2.2 研究区用水量预测

2.2.1因子选取

影响用水量的因子较多，本文根据2002—2020年《宁夏统计年鉴》和《宁夏水资源公报》中的数据，参考已有文献[16-18]，并结合宁夏当地各产业结构，从经济、产品耗水量以及行业相关元素等不同方面选取18个具有代表性的用水量影响因子。其中工业用水选用工业总产值、工业固定资产投资、工业废水排放量、发电量、原煤产值和水泥产量6个因子；农业用水选用农业增加值、农业固定资产投资、万元GDP增加值用水量、单位灌溉面积用水量、粮食产量、全区平均降水、农作播种面积和7个影响因素；生活用水选用人均GDP、平均每人购买水量、城市化率、人口自然增长率、每户居住面积5个影响因子。由于缺乏相关历史数据，本文不计算生态用水。

借助SPSS软件对影响因子和行业用水量进行斯皮尔曼系数相关性分析，利用式(1)得出的计算结果见表1。依据1.1节中对ρs值和P值的相关性划分标准以及参考相关文献[19]，并结合各行业具体计算结果，每个行业分别从经济、产品耗水量、以及行业相关元素3个方面各选取ρs>0.7，P<0.005的一个强相关影响因子，则工业选取的影响因子有工业固定资产投资x1和原煤产量x2；农业选取的影响因子有农业固定资产投资x3、万元GDP增加值用水量x4以及全区平均降水量x5；生活选取的影响因子有人均GDPx6、城市化率x7。

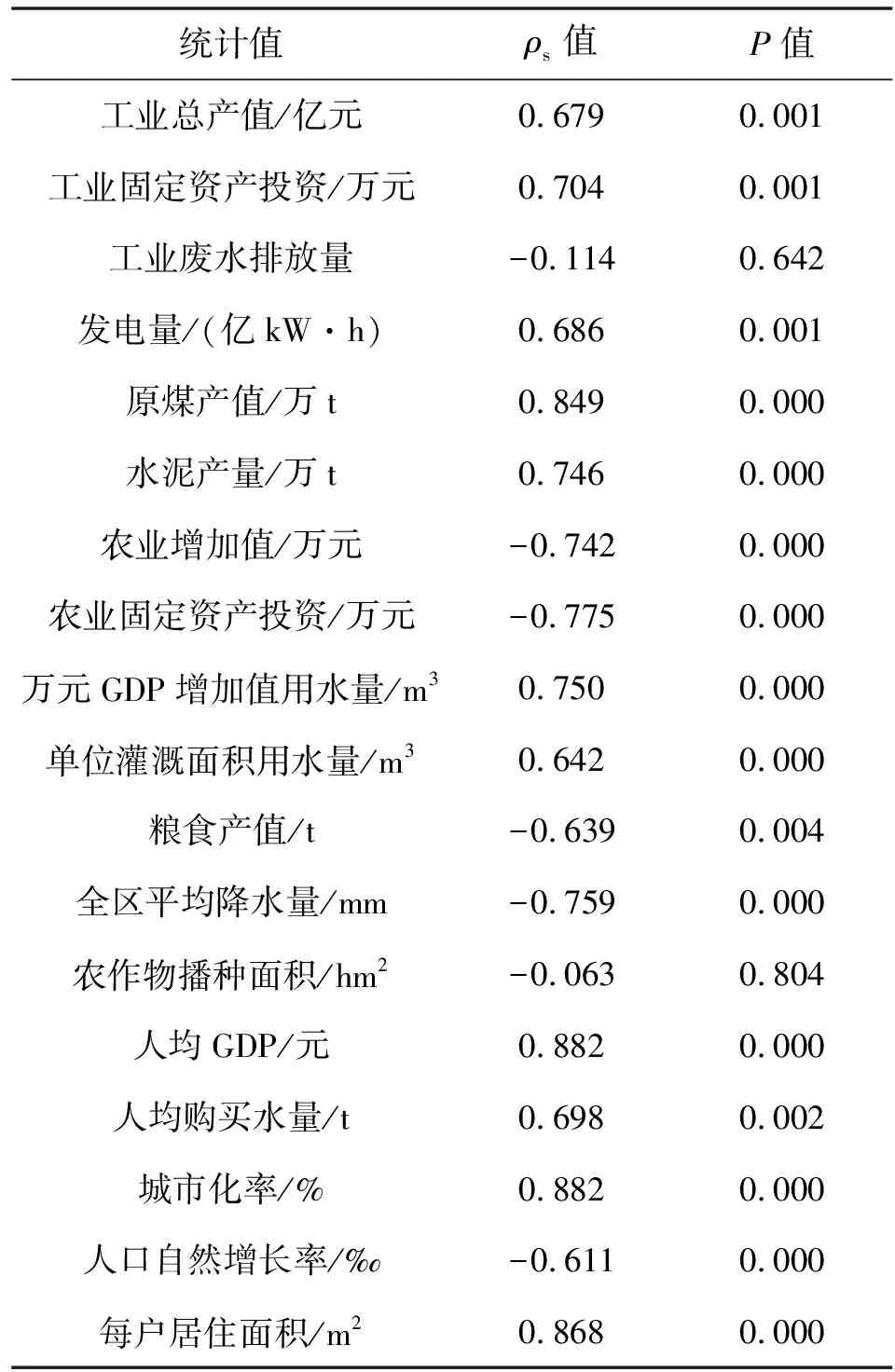
表1 影响因子斯皮尔曼相关系数

2.2.2模型建立

根据3个用水行业各自的不同的特点建立MLP神经网络用水预测模型，根据相关性分析选取工业固定资产投资和原煤产量作为工业用水预测模型的输入节点；选取农业固定资产投资、万元GDP增加值用水量以及全区平均降水量作为农业用水预测模型的输入节点；选取人均GDP、城市化率作为生活用水预测模型的输入节点，各行业的用水量作为模型的输出层节点。通过1.2节的分析，各行业建立用水模型时隐藏层激活函数选择式(2)S型函数，输出层激活函数选择式(4)恒等式函数。为了确定隐含层的节点数，建立了2～10个隐藏层节点个数的MLP神经网络模型结构，均以2002—2016年的各行业用水量和影响因子的数据作为训练样本进行预测。通过比较计算结果，选出最佳隐藏层节点个数，工业、农业和生活用水模型的最优隐藏层节点个数分别为5、6、6个，故得出各行业合适的模型结构，即工业用水模型结构为2-5-1，农业用水模型结构为3-6-1，生活用水模型结构为2-6-1。

2.2.3预测结果及分析

将2017—2020年的数据作为检验样本，用来检测模型的精确程度。各个行业的用水预测结果见表2。

由表2可知，2017—2020年的各行业用水量和总用水量的预测值与实际值相对误差都控制在2%以内。各个行业用水量和总用水量各年的误差均在较小的误差范围内，且总用水量预测值与实际值变化趋势保持一致，说明模型拟合度较高，预测趋势可靠。其中农业用水量预测精度最高，表明农业影响因子选取较为合理。

此外为了检验相关性分析-多层感知器神经网络模型的精度，利用不经筛选的多层感知器神经网络模型训练历年数据，并用此模型预测检测年总用水量，将两者的总用水预测结果进行对比。结果见表3。

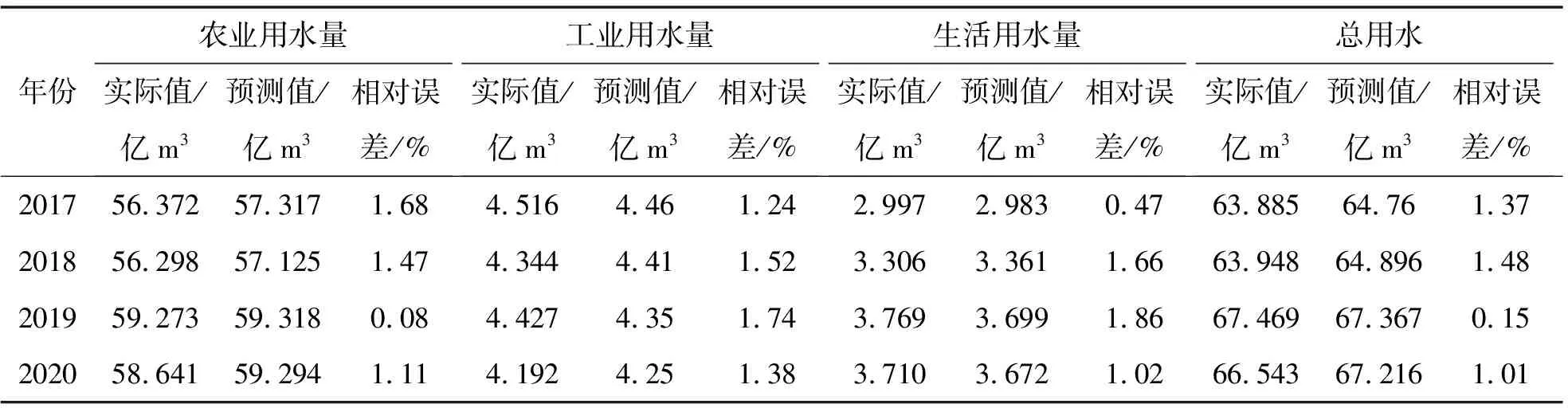
表2 各行业用水预测结果

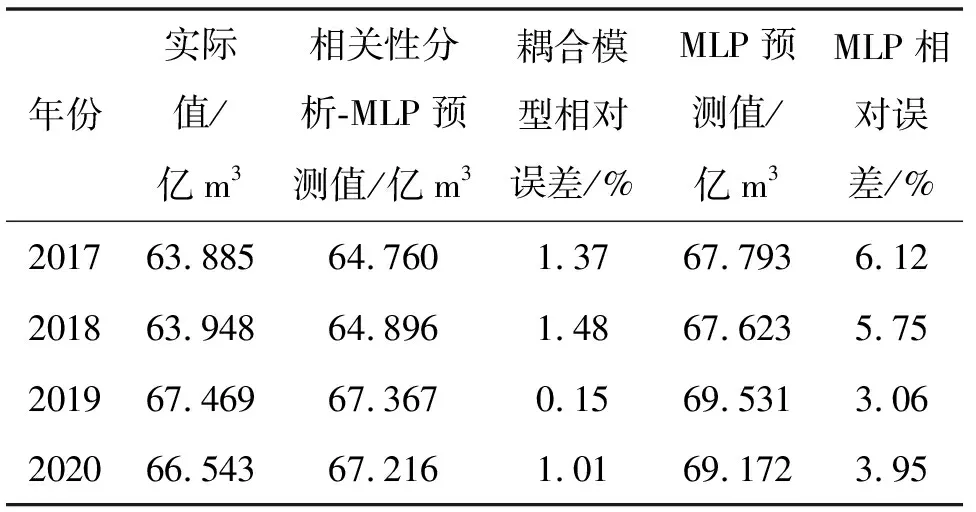
表3 用水预测校验结果

由表3可知，相关性分析和MLP神经网络耦合模型的相对误差均值为1.00%，MLP神经网络模型相对误差均值为4.72%。由此可知，基于相关性分析的MLP神经网络模型预测各行业用水量精度高于直接用MLP神经网络模型预测总用水量的精度。前者在提高了预测精度的同时还减少了模型输入的数据，预测宁夏规划年用水量的时候，前者只需要从不同方面各选取一个相关系数最大的影响因子即可，而后者则需要将所有影响因子都输入模型中；且影响因子经过相关性分析后，能清晰看出各影响因素对各行业用水量的影响程度的大小，采用影响程度更高的因子预测规划年用水量也更为可靠。

2.2.4规划年用水量预测分析

将此耦合模型应用到宁夏回族自治区2025年用水量预测中，根据宁夏回族自治区各行业的“十四五”规划(2020—2025)中的要求，确定相关指标的值，其中全区平均降水量属于随机数据，按照近五年的平均值确定。综上，2025年的各影响因子的预测值见表4。

将以上数据输入训练好的神经网络模型中，预测出2025年宁夏的各行业用水量以及总用水量，具体数值见表5；另外用插值法大致确定2021—2014年的各行业用水量数值，进行加和绘制现阶段到规划年的用水量趋势，见图2，并计算出各年份不同行业的用水占比，见图3。

表4 规划年各影响因子预测值

表5 规划年用水量预测 单位：亿m3

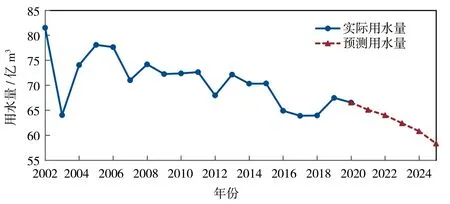
图2 宁夏回族自治区2002—2025年用水量趋势

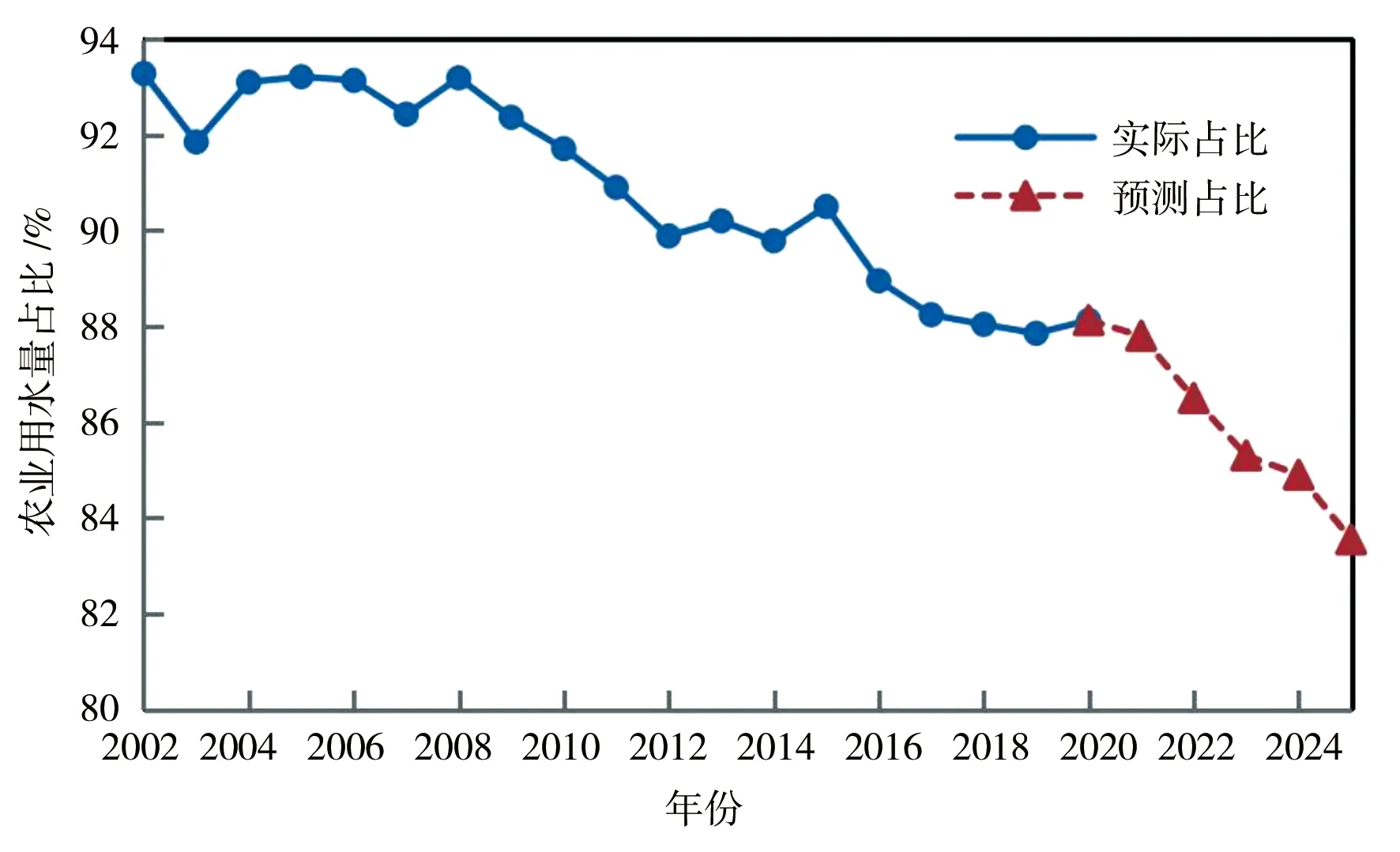
a)农业用水

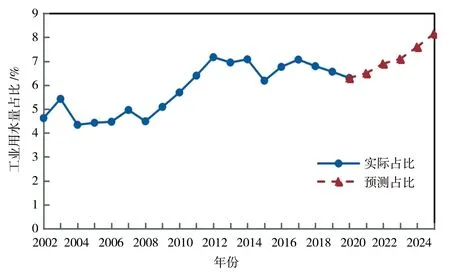
b)工业用水

c)生活用水

由表5、图2的结果可知，2021—2025年宁夏总用水量总体呈较快下降趋势。根据《宁夏回族自治区国民政府和社会发展第十四个五年规划》文件中关于水资源管理三条红线用水总量控制指标要求，到2025年全区取水总量除生态外，大约控制在63.34亿m3以内，预测值达到当地政府的用水量要求。另由图3可知，农业用水占比有一定程度的下降，占比由现状年的88%降到规划年的85%；工业用水占比保持平稳上升，生活用水占比大幅提升，这反映出在2025年全区的用水结构得到进一步优化，具体表现为生活用水量持续得到保障，生产用水量控制在一定的范围内，农业用水量受到严格约束。

3 结论

a)在利用MLP神经网络模型做用水预测之前引入相关性分析，从众多影响因子中筛选出相关性强的影响因子作为神经网络模型的输入值，分别对不同行业进行用水量预测。并与不经过相关性分析处理的MLP神经网络直接预测的结果进行对比，可知这种耦合模型减少了输入节点的数量，明显简化了模型的结构，明确了各个因子对用水量影响程度的大小，且进一步提升了预测精度。

b)利用训练好的相关性分析和MLP神经网络耦合模型预测了规划年2025年的行业用水量以及总用水量，通过预测结果可以看出2025年宁夏总用水量有一定幅度的下降，农业在所有行业用水中的占比依然最高，但和现状年相比农业用水占比有明显下降；工业和生活用水占比均在规划年的基础上有较大幅度的提升。自治区人民政府办公厅印发的宁夏“十四五”用水权管控指标通知中指出，要坚持以水定人、以水定产和以水定地。部分政策如下，到2025年全区灌溉水利用系数提升至0.6以上，全区万元GDP用水量较2020年下降15%，节水器具普及率达到95%等。而此次预测结果充分考虑到这一系列的节水政策，将各个行业的部分约束条件作为模型的输入值，这使得此预测结果具有一定的可靠性，可为自治区水资源规划工作提供相应的参考。