基于改进的TOPSIS算法的企业信贷风险评价
——以中小微企业为例
朱强军
(安徽师范大学皖江学院 电子工程系,安徽 芜湖 241000)
随着我国国有银行商业改革的推进和新型商业银行的诞生,银行的信贷风险管理成为银行生存与发展的关键,加强信贷风险管理逐渐成为我国银行业的共识。我国中小微企业发展迅速,第四次全国经济普查显示,我国共有中小微企业法人单位1807万家,占全部规模企业法人单位的99.8%[1]。党中央、国务院高度重视中小微企业的发展,但中小微企业具有规模相对较小、盈利较低、提供抵押能力有限、金融服务覆盖率低且渠道单一等特点,资金短缺是制约其发展的最主要原因之一。银行信贷风险大,信贷风险管理是银行的当务之急。因此,结合我国中小微企业的实际情况,构建中小微企业信贷风险评估模型尤为重要。对中小微企业的信用风险的评估可以为防范信贷风险提供依据,进而及时控制银行信贷风险的规模,调整银行信贷策略。
国内外学者对中小微企业融资难问题及信贷风险影响因素进行了大量的研究。王权认为,我国商业银行在信贷风险管理方面尚缺乏全面、完整的风险管理建设,风险定量分析不足,信贷风险的研究缺少对信贷内控评价机制的思考[2]。郭小波等在我国中小企业信贷风险识别因子的有效性分析研究中引入财务指标和与企业及企业主特征有关的定性指标作为研究变量,利用二项逻辑回归分析比较了定量数据与定性数据在我国中小企业信用风险识别中的重要性[3]。Vassiliou对印度小微企业信贷案例进行分析,认为信贷风险影响因素主要有贷款人经营理念、经营水平、有无违法记录、贷款利率等[4]。Daisuke Tsuruta对日本部分中小微企业的融资数据进行分析,发现中小微企业的信用低、财务数据缺失、失真等因素是融资难问题的主要原因[5]。葛腾飞等运用KMV模型进行计量分析,将违约概率作为评价指标评判上市公司信用风险状况[6],但该方法评价指标单一,对中小微企业有一定局限性。钱龙在信息不对称条件下分析了银企关系、银行竞争对中小企业信贷风险的影响[7]。迟国泰等认为,信贷风险评价是银行的重要管理活动,评价指标的权重评估又是决定评价结果是否科学的关键环节[8]。赖轩诚应用杠杆效应和Z-score模型分析乐视网所面临的财务风险的严重程度[9],但缺乏对违约评价指标的信贷风险分析。高盼建立了基于财务类评价的指标体系,采用DEA-TOPSIS综合模型对小微企业进行信用评价[10],但缺乏定性评价指标对企业信用的评价。孟好斯运用AHP法对指标赋权,采用统计学比较方法、专家评价法对定量和定性指标赋予评判系数,构建小微企业信用评价模型[11],但该模型依赖评价主体,主观性强,很难客观地为银行等金融机构提供决策。因此,选择中小微企业内定量数据、定性数据以及企业外部信息作为信贷评价指标,构建科学合理的中小微企业信贷评价模型具有重要意义。
一、模型的建立
(一)评价指标的选取与评价模型的构建
风险指标的选取以及风险定性、定量指标的分析在信贷风险控制中尤为重要。根据科学性原则、全面性原则、可行性原则、可比性原则以及定量与定性结合原则[12-14],选取了4个财务指标(营业利润、营业收益率、销售增长率、营业利润增长率)和4个非财务指标(信誉评级、是否违约、进项发票信息的发票状态、销项发票信息的发票状态)进行分析。营业利润为负的企业以及信誉评级较低的企业不予放贷,θi=0表示银行对企业i不予放贷,θi=1表示银行对企业i给予放贷。企业i销项发票信息的价税总计为mi,进项发票信息的价税总计为mi;销项发票中的有效票数为ci,销项发票中的总票数为ti,进项发票的有效票数为di,进项发票中的总票数为ri,将进项发票与销项发票两个指标赋予相同的权重。供求关系稳定系数为ηi,ηj越接近1,表示企业i供求关系越稳定。
根据企业的营业利润和营业收益率,运用TOPSIS(technique for order preference by similarity to ideal solution)算法计算出企业盈利能力系数ξ1,将企业的盈利能力分为强(ξ1>0.3)、较强(0.3≥ξ1>0.2)、一般(0.2≥ξ1>0.08)、较弱(0.08≥ξ1>0.03)、弱(ξ1≤0.03)5个类别,并将分类结果量化得到盈利能力等级χ(见表1)。

表1 盈利能力等级
根据企业的销售增长率和营业利润增长率,运用TOPSIS算法计算出企业状况系数ξ2,将企业状况分为较好(ξ2>0.53)、一般(0.53≥ξ2>0.5)、较差(ξ2≤0.5)3个类别,并将企业状况分类结果量化得到企业状况等级M(见表2)。

表2 企业状况等级
根据信誉评级和是否违约,将信誉评级(A、B、C、D 4个等级,其中信誉等级为D的企业将不予放贷)和是否违约(0表示违约,1表示未违约)分为A0、B1、B0、C1、C0 5个类别,企业分类结果量化得到信誉等级β(见表3)。

表3 信誉等级
(二)决策模型的建立
对中小企业信贷策略的研究,主要从盈利能力、企业状况、信誉等级、供求关系这4个主要指标进行分析,向实力强、供求关系稳定的企业提供贷款,并可以对信誉高、信贷风险小的企业给予利率优惠,构建企业基本状况的1个一级决策指标、4个二级决策指标、8个三级决策指标。详情见表4。

表4 企业借贷决策指标
反映企业盈利能力的财务指标很多,选取营业利润和营业收益率两项指标评价企业的盈利能力;企业状况是评价企业的成长状况和发展状况的,选取评价成长状况的销售增长率指标和评价发展状况的营业利润增长率指标;信誉为银行对企业的信任程度,企业的信誉越高,银行对企业的风险评估越小,贷款的成功率增大;供求关系是评价企业的供求稳定状态的,有效发票占总票数比例大,代表供求关系稳定,反之则供求关系不稳定。信贷风险平稳系数由盈利能力、企业状况、信誉等级、供求关系4个二级决策指标共同影响。4个二级决策指标分别由8个三级决策指标决定,每2个三级决策指标决定1个二级决策指标。
企业i第j年销项发票信息的价税总计为mij,进项发票信息的价税总计为nij,该企业的营业利润为:
Mi=mi-ni
(式1)

该企业营业收益率为:
(式2)
根据式1、式2的计算结果,运用TOPSIS算法计算出企业盈利能力系数ξ1。
该企业销售增长率为:
(式3)
该企业营业利润增长率为:
(式4)
根据式3、式4的计算结果,运用TOPSIS算法计算出企业状况系数ξ2。
销项发票中的有效票数为ci,销项发票中的总票数为ti,销项发票的有效系数为:
xi=ci/ti
(式5)
进项发票中的有效票数为di,进项发票中的总票数为ri,进项发票有效系数为:
yi=di/ri
(式6)
销项发票的有效系数和进项发票有效系数被赋予相同的权重,供求关系稳定系数为销项发票的有效系数和进项发票有效系数的均值,供求关系稳定系数为:
ηi=(xi+yi)/2 (0≤ηi≤1)
(式7)
供求关系稳定系数越大,企业的供求关系越稳定。运用熵权-TOPSIS算法综合盈利能力、企业状况、信誉等级以及供求关系4个二级决策指标获得信贷风险平稳系数。
二、熵权-TOPSIS算法的中小微企业信贷风险评价
TOPSIS算法由Hwang和Yoon[15]于1981年提出,是为了解决系统工程中有限方案的多目标决策问题的,是距离综合评价法。近年来,该算法被用于风险决策分析、土地整理实施效益评价以及绩效评价等多个方面[16-19],取得了成功,但该算法将不同影响因素的重要程度默认为相同,即指标的权重相同,这与实际情况不符。熵权法[20]是一种客观赋权方法。1948年,Shannon将物理中的熵引入到信息论中度量数据携带的有效信息量,所以熵可以用来确定权重值[21]。本文采用熵权法与TOPSIS算法相结合即熵权-TOPSIS算法评价企业信贷风险。
根据企业的盈利能力、企业状况、信誉等级以及供求关系稳定系数4个评价指标构成原始矩阵A:
供求关系稳定系数为极大型指标,盈利能力等级、企业状况等级、信誉等级为极小型指标。正向化处理时,极小型指标转化为极大型指标为:
μ′=max-μ
(式8)
对矩阵A正向化,得到矩阵X:
通过正向化矩阵X计算概率矩阵为:
(式9)
计算每个指标的信息熵,设第j个指标的信息熵ej为:
(式10)
求信息效应值dj:
dj=1-ej
(式11)
对dj归一化得到熵权:
(式12)

(式13)

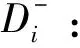
(式14)
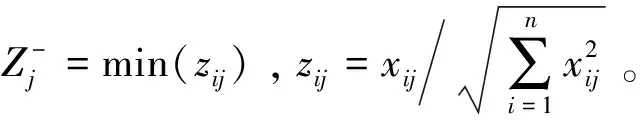
计算评价对象i的得分Si,计算公式为:
(式15)
通过熵权-TOPSIS算法对各个指标客观赋权,得到信贷风险平稳系数Γ。Γ值越大,企业信贷风险越小;Γ值越小,企业信贷风险越大。熵权-TOPSIS算法流程如图1所示。

图1 熵权-TOPSIS算法流程
三、实证分析
构建的信贷风险决策模型由多种定性和定量指标组成。为了保证数据的真实性、准确性和有效性,文中所涉及的企业信息以及定性、定量指标数据皆来源于2020年全国大学生数学建模竞赛的123家有信贷记录的中小微企业的相关信息。
根据企业的进项发票和销项发票的合计税额得到123家企业的进项价税总计和销项价税总计,从而获得三级决策指标企业的营业利润,将营业利润为负或信誉评级为D的企业不予放贷,共计30家。不予放贷的30家企业的情况见表5。
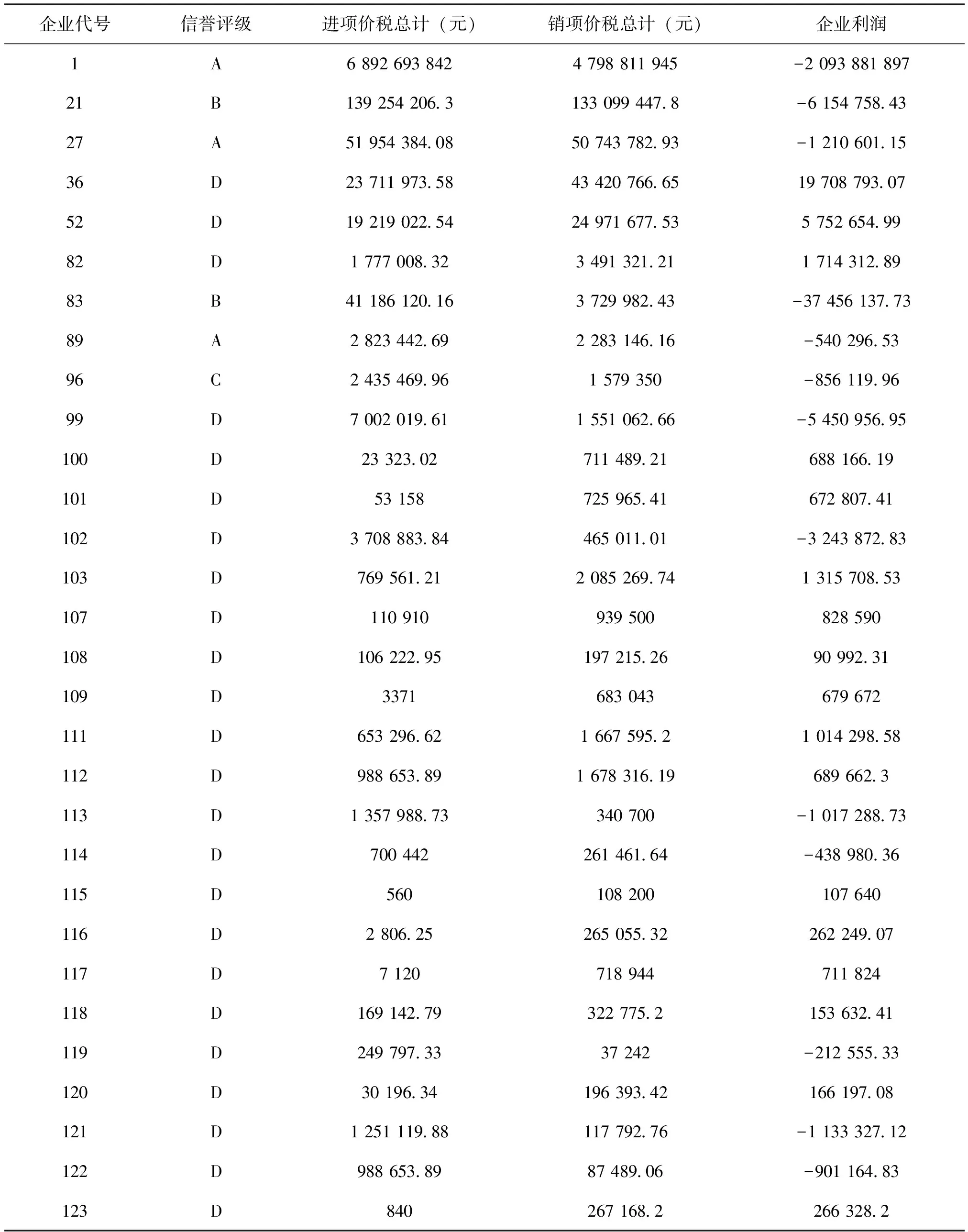
表5 不予放贷的30家企业的情况
对于营业利润非负且信誉评级高于D的93家企业,利用TOPSIS算法计算出企业盈利能力系数和企业状况系数。具体如图2所示。

图2 盈利能力系数和企业状况系数
根据系数将企业盈利能力和企业状况量化成企业的盈利能力等级和企业状况等级。盈利能力等级如图3所示,企业状况等级如图4所示。
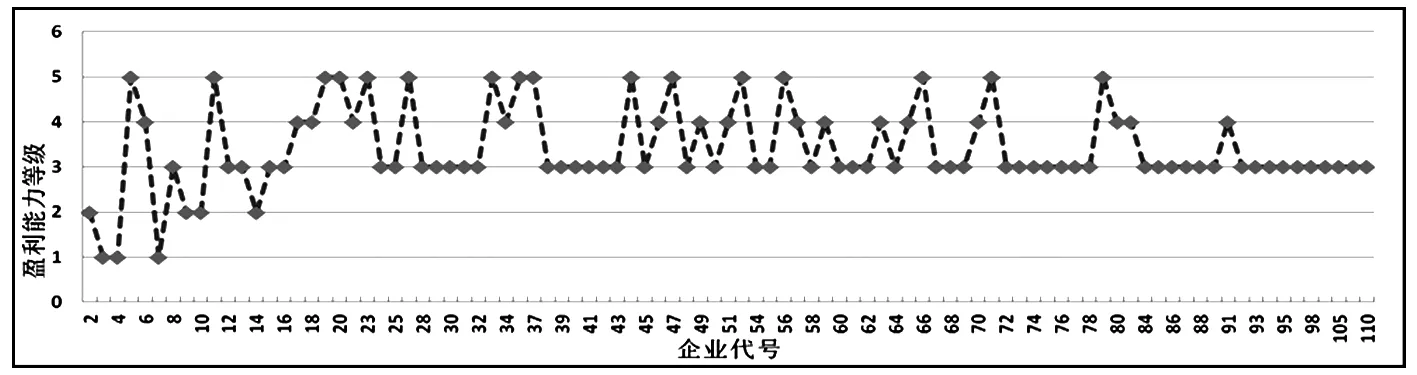
图3 盈利能力等级
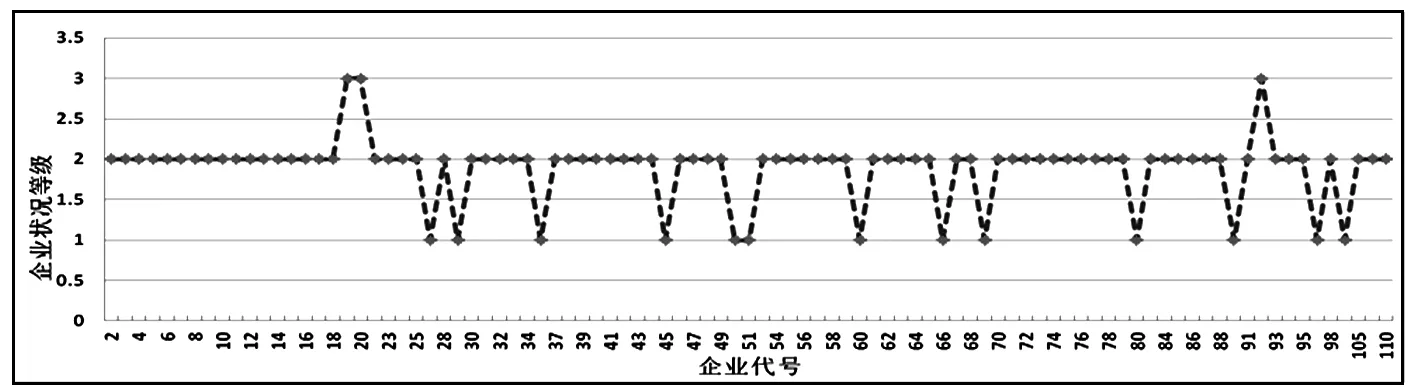
图4 企业状况等级
根据信誉评级和是否违约得到的信誉等级如图5所示;根据进项发票和销项发票的有效状态得到进项发票和销项发票的稳定系数,进而得到的供求关系稳定系数如图6所示。
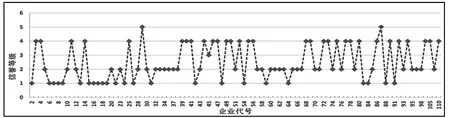
图5 信誉等级

图6 供求关系稳定系数
根据盈利能力等级、企业状况等级、信誉等级、供求关系稳定系数获得信贷风险平稳系数Γ。
首先,通过熵权-TOPSIS算法对原始数据标准化处理,得到4个指标的标准化矩阵Z,将标准化后矩阵每列的最大值和最小值分别合并得到最大值向量Z+和最小值向量Z-。最大值向量与最小值向量见表6。

表6 最大值向量与最小值向量
其次,将企业的4个指标量化构成正向化矩阵X,用正向化矩阵各列归一化得到概率矩阵P,由概率矩阵计算出各个指标的信息熵e,利用信息熵定义信息效应值并将其归一化得到熵权值W。盈利能力等级、企业状况等级、信誉等级、供求关系稳定系数熵权值见表7。

表7 指标熵权重
最后,通过最大值向量、最小值向量计算各个评价指标到正、负理想解之间的欧氏距离D+、D-,综合各个指标与正、负理想解之间的欧氏距离计算出得分S,将得分S定义为信贷风险平稳系数Γ。93家企业信贷风险平稳系数如图7所示。

图7 信贷风险平稳系数
从图7可知,企业代号为2、3、4、7、9、10的6家企业的信贷风险平稳系数明显高于其他企业,银行放贷风险低,可以为这类企业提供较大的信贷额度以及制定较优的信贷策略;企业代号为11、44、47、53、56的5家企业的信贷风险平稳系数明显低于其他企业,银行放贷风险高,不宜给予放贷。
四、结论和建议
(一)结论
我国中小微企业数量巨大,融资缺口大,银行每年都能接到大量的中小微企业的贷款申请,但中小微企业规模小、能抵押的资产少、信誉风险高、信息不透明,而银行需要稳健经营,所以建立科学合理的中小微企业信贷风险评价模型尤其重要。本文根据国家信贷政策、基于企业交易票据等信息,建立了一个中小微企业信贷风险评价模型。该模型综合考虑中小微企业的盈利能力、状况、供求关系等因素,从多角度挖掘出8个三级决策指标,通过三级决策指标中的营业利润、信誉评级剔除不符合要求的中小微企业,对符合要求的中小微企业利用三级决策指标并使用TOPSIS算法得到各企业的相关系数,再量化成等级,构成二级决策指标。采用熵权法对二级决策指标客观赋权,利用TOPSIS算法得到信贷风险平稳系数。根据中小微企业的信贷风险平稳系数,银行等金融机构为中小微企业提供贷款策略。在123家有信贷记录的中小微企业中进行验证,得出如下结论:
第一,该模型选取影响信贷风险的指标较全面。选取影响信贷风险的4个财务指标和4个非财务指标共8个三级决策指标,较为全面地覆盖了影响中小微企业信贷风险的因素,减少了信贷风险评价的主观性影响,增强了客观性。
第二,该模型构建了3个等级的决策指标,最终获得评价中小微企业信贷风险大小的一级决策指标信贷风险平稳系数。利用8个三级决策指标确定盈利能力等级、企业状况等级、信誉等级、供求关系稳定系数4个二级决策指标,采用熵权法对这4个二级决策指标客观赋予权重,利用TOPSIS算法对所采集的定性、定量数据进行预处理以及量化转换,消除各个二级决策指标之间的量纲及相关影响,得到归一化的一级决策指标信贷风险平稳系数。根据中小微企业的信贷风险平稳系数差异,银行等金融机构为中小微企业提供不同贷款决策。
第三,该模型在123家有信贷记录的中小微企业中得到验证。该模型有效可行,可以为银行等金融机构对中小微企业信贷风险评价提供理论支撑和参考依据。
(二)建议
为了更好地解决中小微企业融资难以及银行信贷风险大等问题,中小微企业信贷风险评价模型可以进一步深入研究的方向如下:
第一,信贷风险评价模型与大数据技术相结合。基于大数据技术能解决中小微企业的数据失真、信息不透明等问题,同时,利用大数据挖掘和分析技术可以实时处理数据,动态调整中小微企业的信贷风险平稳系数。
第二,引入中小微企业行业结构和供应链情况的决策指标。根据中小微企业主要经济活动性质进行行业分类,结合中小微企业所在的行业、行业中所处供应链的上下游情况以及供应链中地位的重要性,建立不同行业的中小微企业信贷风险评价模型。

