一类有限链环上的厄米特自正交码

钟家伟

(安徽信息工程学院 通识教育与外国语学院，安徽 芜湖 241000)

量子纠错码(QECCS)理论被广泛应用于量子通信中，解决因消相干对抗噪声引起的误差问题。对于由维数q≥2的n个子位组成的量子位，即所谓的量子比特，量子码C=((N,K))q是Hilbert空间(Cq)⊗n的k维子空间。若码C的维数qk,则记C=[n,k,d]q，其中，d是码C极小距离。最小距离d的码能够纠正不超过1+d/2的子位的错误。量子纠错码的Singleton界满足：n-k≥2(d-1)，若等号成立，则称此量子码为量子MDS码。

文献[1]提出了将量子码的研究转化为对厄密特自正交码的构造问题，自此，对厄密特自正交码的研究逐渐成为编码爱好者研究的重点。文献[2]研究了有限链环Fq+uFq上的循环码为自正交码的等价条件；文献[3]研究了剩余类环Z2m上循环自正交码的结构方法。文献[4]研究了q元域上的上最大极小距离大于1+d/2循环自正交MDS码的结构方法。同时，利用有限环上的自正交码构造了许多具有良好参数的量子最优码或渐进优码[5-8]。文献[9]根据有限域上线性码是厄米特LCD码和厄米特自正交码的判定条件，构造出了4类四元厄米特LCD码和厄米特自正交码。文献[10]构造了q元域上的广义厄米特自正交MDS码存在的充要条件，并构造几类具有极小距离的量子码。

1 基础知识

令R=Fpm，Rn为R上为长为n的线性码，Rn[x]=R[x]/(xn-1)，给定任意λ∈R*,定义R上的λ常循环移位为σλ(x0,x1,…,xn-1)=(λxn-1,x0,…,xn-2)。若令C是R上长为n的码字，对于任意码字c∈C都有σλ(C)∈C成立，则称C为λ常循环码,特别地,当λ=1时,有σ(C)=C成立，则称C为R上的循环码。

假设x=(x0,x1,…,xn)和y=(y0,y1,…,yn)是R上任意的两个长为n的码字，定义x,y的欧几里得内积为：

x·y=x0y0+x1y1+…+xn-1yn-1。

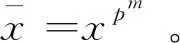
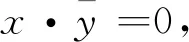
设C是为[n,k]线性码，定义码C的对偶码为：

定义码C的厄米特对偶码C⊥H为：

若C⊆C⊥，则称C为自正交码；若C=C⊥，则称C为自对偶码；若C∩C⊥={0},则称C为LCD码。若C⊆C⊥H，则称C为厄米特自正交码；若C=C⊥H，则称C为厄米特自对偶码；若C∩C⊥H={0}，则称C为厄米特LCD码。

令α=(α0,α1,…,αn-1)∈Rn，其中，αi∈R，i=1,2,…,n-1，R*表示R的非零子集，v=(v0,v1,…,vn-1)∈(R*)n，定义广义R-S码[9]为：

GRSk(α,v)={(v0f(α0),v1f(α1),…,vk-1f(αk-1))|f(x)∈Rn[x],deg(f(1))≤k-1}。

易得，GRSk(α,v)的生成矩阵为：

则GRSk(α,v)为R上的参数为[n,k,n-k-1]的MDS线性码，易知其对偶码也是MDS线性码。

令R=Fq+uFq={a+ub|a,b∈Fq}，其中，u2=0。环R是一个局部有限链环，环R上长为n的线性码是Rn的R-子模。

2 环R上的厄米特自正交码

假设C是环R上长为n的线性码，则定义C的剩余码C1以及挠码C2分别为：

根据中国剩余定理可知C=(1+u)C1⊕uC2。

定义2.1R到R的广义Gray映射:

θ(a+bu)=(b,a+b)，

Rn到R2n的保距映射:

φ(c)=(b,a+b)，

其中，c=(a0+ub0,a1+ub1,…,an-1+ubn-1)，a=(a0,a1,…,an-1)，b=(b0,b1,…,bn-1)。

定义2.2[11]对任意的a∈R，定义R到N的齐次重量函数wt(a)：

a

设C为R上的线性码，则定义C上任意码字c=(c0,c1,…,cn-1)∈C的齐次重量wt(c)定义如下：

齐次距离d(C)定义为：

d(C)=min{wt(c)|c≠0,c∈C}。

取R中的向量：v=(1,1,1,…1)，w=(0,1,2,…pm-1)，

令：c0=w⊗v;c1=v⊗w，

其中，⊗表示R上的张量积运算。

定义2.3对于R中任意元素x都可唯一表示为：

x=a+bu，

其中a,b∈R。若存在映射φ使得：

φ(x)=ac0+bc1，

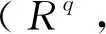
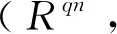
引理2.5设C为R上长为n的线性码，φ(C)是的广义Gray映射，则：

d(C)=dh(φ(C))。

引理2.6[9]令1≤t≤q，则：

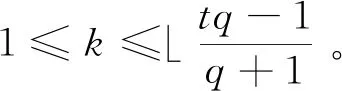
(2)当n=t(q+1)时,R上参数为[t(q+1),k,t(q+1)-k+1]厄密特自正交MDS码存在的充要条件为1≤k≤t-1。

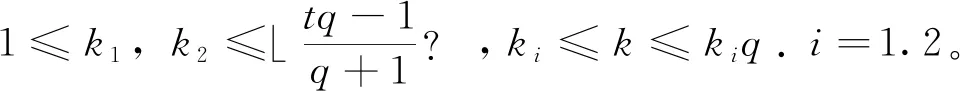
证明：由C1,C2为长为t(q-1)的自正交码,由引理2.5知φ为R到R的保距映射故R上厄密特自正交码的极小距离等于R上线性码φ(C)的极小距离且也为MDS码。由于C=(1+u)C1⊕uC2,根据所定义的齐次距离，C的信息位k满足ki≤k≤kiq，i=1.2。综合引理2.6中C1、C2所给参数，可证得C的参数为[t(q-1),k,d(φ(C))]。

同理可得，当n=t(q+1)时的情形。

定理2.8 设C=(1+u)C1⊕uC2为R上参数为[t(q+1),k,d(φ(C))]的厄密特自正交MDS码的充要条件为C1为参数[t(q+1),k1,t(q+1)-k1+1]的厄密特自正交MDS码，C2为参数[t(q+1),k2,t(q+1)-k2+1]的厄密特自正交MDS码，其中1≤k1,k2≤t-1，ki≤k≤kiq.i=1.2。

推论2.9设C为R上长为n的厄密特自正交MDS码，则φ(C)为R上长为nq的厄密特自正交MDS码。

推论2.10设C为R上长为n的厄密特自正交MDS码，则设C⊥也是R上长为nq的厄密特自正交MDS码。

3 应用举例

例3.1当q=4,t=2时，根据引理3.6(1),则存在四元[6,3,4]厄米特自正交MDS码和四元[6,4,3]厄米特自正交MDS码，根据定理3.7，则存在F4+uF4上参数为[6,4,3]的自正交MDS码。

例3.2当q=9,t=5，根据引理3.6(2)，则存在四元[50,42,9]厄米特自正交MDS码和四元[50,45,6]厄米特自正交MDS码，根据定理3.8则存在F4+uF4上参数为[50,42,9]的自正交MDS码。

4 结语

有限域上量子码的研究已逐渐成熟并已运用于量子通信领域中，但对于有限环上量子码的研究尚处于初级阶段，有限环的上的自正交码研究为构造MDS量子码奠定了理论基础。通过所定义有限环上的齐次重量到有限域上的汉明距离的保距广义Gray映射，构造了域上厄密特自正交MDS码的方法。后续可对其他有限环上自正交码和量子码、有限非链环上的自正交码和量子码以及重量分布、周期分布、覆盖半径等相关性质开展研究。