单模块装药点火燃烧过程中端盖破裂形态对药粒散布的影响

杨旭光，余永刚，陈 安

(南京理工大学 能源与动力工程学院，江苏 南京 210094)

引 言

现代战争极具作战突然性，兼有武器破坏性强，精准度高，战场空间愈加立体化、多维化，物资消耗大，后勤保障难等特点。对于大口径野战炮而言，如何在保证其毁伤性和精准度的同时，提高其战场生存能力和快速反应能力已成为重中之重。因此，一种满足火炮各装药号自动装填、减轻后勤供应压力、提高火炮快速反应能力的模块装药技术应运而生。然而，在小号装药点火燃烧过程中，此时药室内模块装填数(1至2个)较少，一旦药盒破裂，药粒必然边飞散边燃烧，在弹丸启动前药粒群会先形成一定的堆积形态，随着膛内燃烧压力升高，弹丸启动，从而形成复杂的气固两相反应流。同时，药粒初始堆积的越不均匀，膛内初始燃烧压力波必然越大，这会导致武器系统的弹道性能变差，严重时会发生安全事故。

模块药盒在火炮膛内点火燃烧，将产生复杂的气固两相反应流。陆中兵、周彦煌[1]为了精确模拟模块装药火炮膛内的压力波动，基于二步差分法，建立了准二维两相流内弹道模型。其计算结果与测试结果吻合较好，对该类问题的研究具有重要参考价值；王育维[2]针对小号装药的实验结果进行数值仿真，分析得出影响药室内压力波的主要因素为：药床长度、单一模块药盒装药量；该研究对确保小号装药发射系统的安全性和稳定性具有重要意义；赵毅[3]建立了一维两相流模型,采用Runge-Kutta法模拟组合装药的点火过程,将多种点传火方案的计算结果和测试结果进行了对比分析；周瑶[4]通过改变传火通道直径和传火药的种类及质量，针对模块装药全装药方式开展了6种点传火结构方案的实验研究，获得传火时间及传火速度等参数，优选出了一种最佳的全装药点传火方案。之后，有关模块装药的研究主要集中在烤燃特性[5-7]、装药结构[8]、燃烧残渣[9-10]以及弹道性能[11-14]等方面。以上研究对于模块药盒燃烧破裂后，药粒的飞散分布模型均按照均匀分布或按某一固定形状分布假设处理。然而实际情况下，药粒的最终堆积分布并不均匀，这对炮膛内起始压力波有着重要影响。

为了研究小号装药模块破裂后，药粒的散布形态，采用颗粒燃烧“冻结”方法，即在模块中装填不燃烧的模拟药粒和部分真药粒。在点火射流作用下，真药粒燃烧导致药盒破裂，模拟药粒飞散，形成一定的堆积形态。通过这种模拟实验方法，可近似获得模块药盒破裂后火药颗粒的初始散布形态。陈安率先对单模块[15]、双模块装药[16]点传火过程中药盒破裂后，药粒散布特性进行了模拟实验与仿真，得到了模拟药粒的终态堆积分布特性及初始装填位置对药粒散布形态的影响。上述结果对认识模块装药点传火过程中颗粒的堆积分布有重要参考价值。但以上数值研究均为假设点传火中模块药盒端盖整体打开，这与模拟实验观测到的端盖破裂形态不完全相符。

药盒端盖先破口区域分为中心局部破口、边沿破口、中间破开等方式，随后由于燃烧压力升高，整个端盖飞离药盒，这是由于药盒材料、燃烧不均匀等原因，导致药盒端盖破裂形态有一定的随机性。为此，本研究基于流固耦合方法，建立三维非稳态气固两相流模型，对模块药盒端盖不同破孔方式下的药粒堆积形态进行数值模拟，研究结果对深入分析膛内起始压力波动有一定参考价值。

1 理论模型

基于流固耦合方法，建立单模块装药药盒破裂后药粒散布的三维非稳态气固两相流模型，并做出如下假设：

(1)模块药盒在点火燃烧破裂时，端盖以某种形态先行破开。

(2)将药粒做拟球体处理，并忽略颗粒相与气相的传热作用。

(3)由于药室内仅有一个模块，属于稀疏相，因此不考虑固相对气相的影响。

(4)采用Hertz-Mindlin无滑动接触模型来处理颗粒与颗粒、颗粒与药室壁面间的碰撞。

(5)药室内气相的湍流运动运用Realizablek-ε模型进行处理。

(6)忽略点火时模块盒在燃气冲击下的运动。

1.1 气相控制方程

气相质量守恒方程：

(1)

气相动量守恒方程:

(2)

气相能量守恒方程:

(3)

式中：ρg为药室内气体密度，kg/m2；vg为气体的运动速度，m/s；P为药室内气体压强，N/m2；e为单位气体所具有的能量，J/kg。

1.2 药粒运动方程

药粒在点传火燃气流作用下的运动方程如下：

(1)平动方程：

(4)

Fd=βgs(vg-vs)

(5)

(6)

(7)

Rep=ρgεg|vg-vs|Ds/μg

(8)

Fg=msg

(9)

式中：ms为模拟发射药粒的质量，kg；vs和vg分别为点传火过程中固相和气相的速度，m/s；Fd为药粒所受曳力，N；Fg为药粒自身的重力，N；Fc为颗粒与颗粒、颗粒与药室壁面间的碰撞力，N；βgs为曳力系数，N·s·m-1；ρg为气相密度，kg/m3；εg和εs分别为气相和固相在网格内的体积分数；Rep为药粒雷诺系数；Ds为药粒直径，m；μg为气相黏性系数，Pa·s。

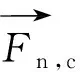
(10)

(11)

(12)

(2)转动方程：

(13)

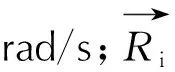
2 计算模型及验证

2.1 计算模型

应用EDEM和FLUENT两种仿真软件，对单模块装药点火燃烧过程中的药粒散布进行耦合运算。对此三维非稳态气固两相流问题，采用如图1所示的计算模型。其中，模块药盒距药室左端40mm，药室内颗粒相和气相的初始状态均为静止状态，初始气压为标准大气压(101325Pa)，药盒端盖初始破口压力P1(6MPa),药盒端盖整体打开压力P2(10MPa),初始温度为300K。求解时选择基于压力求解，压力-速度耦合采用SIMPLEC模式，密度、压力、动量、能量方程均使用二阶迎风格式，计算步长取1×10-6s。

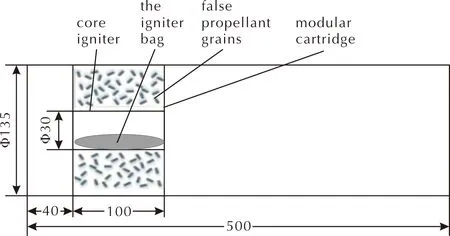
图1 计算模型Fig.1 Computational model

2.2 网格无关性验证

对图1所示的模型采用结构化网格进行划分，已知药粒拟球体直径为10.76mm，根据网格尺寸需大于颗粒直径的计算限定条件，依次选取网格尺寸为11、12和18mm的3种网格划分类型进行模拟计算，在药室药粒堆积区域内，沿轴向位置取与实验位置相同的6个特征点，测得各点的药粒模拟堆积厚度,仿真结果如图2所示。

图2 不同网格划分计算结果比较Fig.2 Comparison of calculation results with different meshing

以11mm网格划分类型的模拟值为基准，分别计算12mm和18mm的两种网格划分类型下6个位置药粒模拟堆积厚度与这一基准的平均误差，计算可得：误差依次为1.12%和9.76%。考虑到网格尺寸为18mm时，模拟值间的平均误差较大，因此不使用这一种网格划分；而网格尺寸为11mm和12mm的两种类型，模拟值间的平均误差较小，为了兼顾计算效率和计算精度，本研究选择12mm的网格进行后续计算。

2.3 模型的实验验证

为了验证计算模型，采用文献[15]所得到的单模块装药实验结果，模拟药粒的最终堆积形态如图3所示。在药粒的陡坡状堆积区域选取6个特征点，分别测量其距底火侧的水平距离(X)及各处药室内壁面最低点和药粒堆积最高点的高度差(h),结果见表1。

图3 点传火平台中药粒最终堆积形态Fig.3 Final stacking morphology of propellant grains on ignition-transfer platform

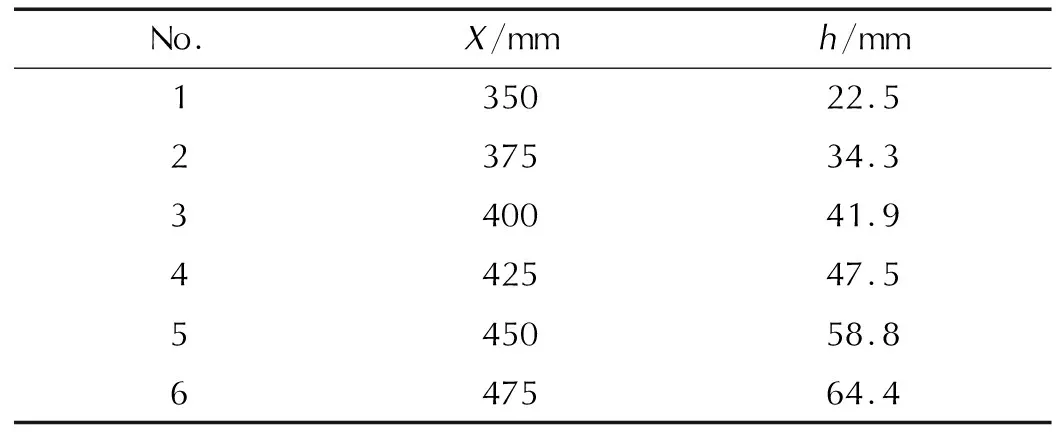
表1 药粒堆积高度的实验测量值Table 1 Experimental measured values of grain stacking height

将各点测得的药粒堆积厚度与数值模拟结果进行比较，如图4所示，两者的平均误差为4.7%，计算与测量结果基本吻合，验证了模型的合理性。

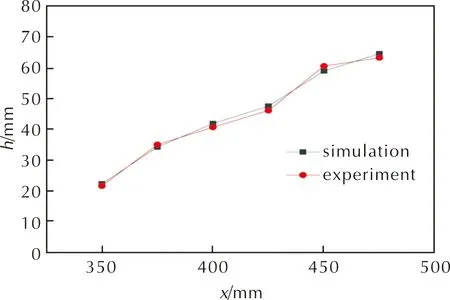
图4 h的模拟值与实验值的对比Fig.4 Comparison of simulated and experimental h value

3 药粒散布的数值预测

实验时发现药盒端盖在压力较低时会先破裂一部分，分析原因认为是药盒材料、燃烧不均匀等导致。在药室内压力达到端盖整体破开压力时，端盖整体打开。这种药盒端盖打开方式，会对药室内药粒的最终堆积形态产生一定影响。针对这一问题，分别对端盖不同破孔方式下的药粒散布特性进行数值模拟，探究模块药盒破孔方式对药粒散布特性的影响。

3.1 端盖初始破孔大小对药粒散布特性的影响

为了探究药盒端盖先破开部分的大小对药粒散布特性的影响，如图5所示，假设阴影区域为端盖先行破孔的区域，其对应的扇形夹角为θ，分别对θ取值30°、60°、90°和120°的4种工况进行数值模拟。模拟中假设药盒端盖初始破口压力均一致。4种不同工况下药室内药粒的最终堆积形态如图6所示。

图5 端盖先破口部分示意图Fig.5 Schematic diagram of the priority broken sector in the end cap

图6 端盖不同大小破孔下药粒的最终堆积形态 Fig.6 Final packing morphology of propellant grains under different broken sector sizes of the end cap

由图6可以观察到，药室的药粒堆积均从左至右呈3种堆积状态，依次为缓坡堆积、水平堆积和陡坡堆积，但各形态的形状特征参数不同。随着θ逐渐增大(即先破开部分面积的增大)，其中水平堆积的轴向终止点向右移动，水平堆积部分的平均药粒厚度逐渐增高，陡坡堆积部分药粒在总药粒数的占比逐渐减少。为了更好地表示药粒堆积特性，引入3个特征参数，分别为缓坡和水平堆积的总轴向长度l, 水平堆积部分的平均药粒厚度d和陡坡部分药粒堆积占比α。分别对4种工况的堆积结果进行测量，数据整理如表2所示。

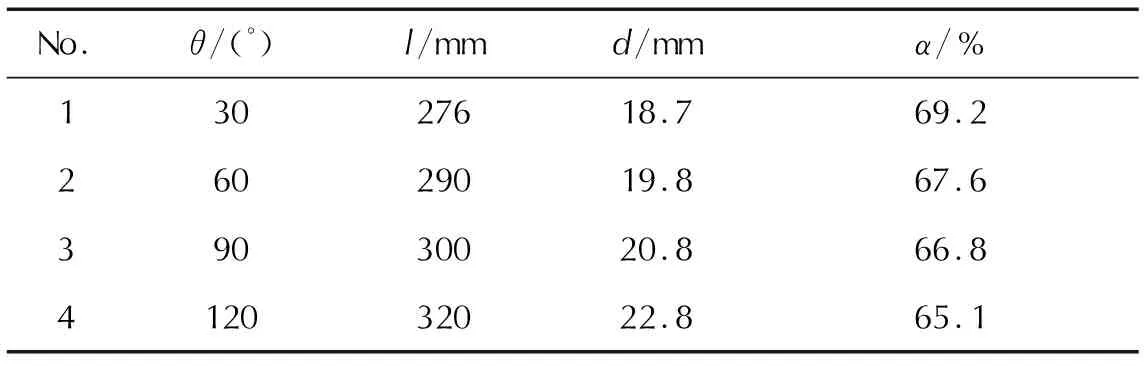
表2 不同破孔大小下药粒堆积测量结果Table 2 Measured results of accumulation of grains under different broken sector sizes

由表2可知，随着θ由30°增至120°，缓坡和水平堆积的轴向长度由276mm增至320mm，水平堆积部分的平均药粒厚度由18.7mm增加至22.8mm，陡坡状药粒堆积占比由69.2%减少至65.1%。这是由于模块药盒端盖某部位先破孔时，药盒内压力相对较低，先打开的破口越大，尽管药粒的初始流量较大，但药粒获得的加速度较小，药粒彼此间相互碰撞，减速、停止的就会较多，运动到药室右侧的药粒数会相对较少。因此，药盒端盖先破开部分越大，缓坡和水平堆积长度越长且药粒的平均堆积厚度越厚，同时导致陡坡状药粒堆积占比越少。

如药盒没有先行破孔，一直到药盒内压力较高，出现端盖整体打开，即相当于初始破孔扇形夹角θ为0这一特殊情况，测得初始工况缓坡和水平堆积的轴向长度为269mm，水平堆积部分的平均药粒厚度为18.1mm，陡坡状药粒堆积占比为70.3%，通过与表2几种工况对比，发现与上述规律一致。

3.2 端盖初始破孔位置对药粒散布特性的影响

实验时发现药盒端盖先破孔部分位置的不同也会对药室内药粒的最终堆积分布产生影响，同时这一破孔位置上下、左右方位的差异对药粒分布特性的影响也各不相同。因此，分别就初始破孔位置，端盖的上、下部位和左、右部位两类情况进行数值模拟。

3.2.1 药盒端盖上下部位先破开工况

为了探究药盒端盖先破开部位对药粒散布特性的影响，如图7所示，分别选取端盖先行破孔的区域对应的扇形夹角θ同为30°、120°，但位置分别处于端盖的上半部区域和下半部区域4种工况进行数值模拟。 4种不同工况下药室内药粒的最终堆积形态如图8所示。

图7 端盖上下初始破孔部位示意图Fig.7 Schematic diagram of priority broken sector in the top/bottom of the end cap

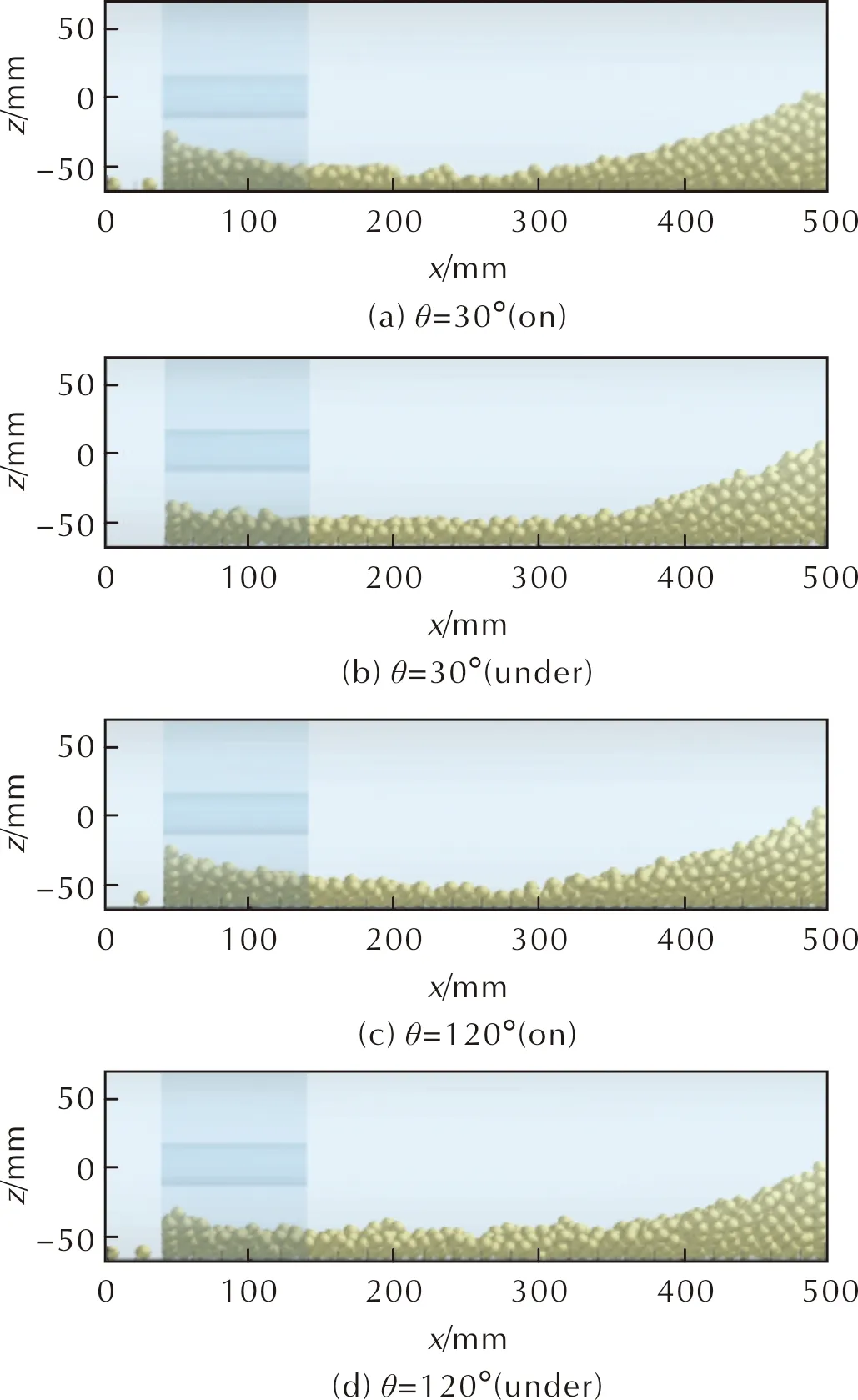
图8 端盖先破孔部分上下不同分布所对应的药粒堆积终态 Fig.8 Final state of grain accumulation corresponding to the different priority broken sectors in the top/bottom of the end cap

由图8可以观察到，4种不同工况下药室内药粒均从左至右依次为缓坡堆积、水平堆积和陡坡堆积的最终堆积状态，但各形态的形状特征参数不同。为了更好地分析药粒分布特性，仍采用3个特征量l、d、α分别对4种工况的堆积结果进行测量，数据整理如表3所示。药粒碰壁后药室内流场速度矢量分布如图9所示。分别将工况1与工况2、工况3与工况4的数据进行对比可知，模块药盒端盖下半部分较上半部分先破孔，药粒缓坡和水平堆积长度更长，且平均药粒堆积厚度更厚，陡坡状药粒堆积占比更少。主要原因为：端盖上半部分先破孔的工况中，当药室内上半部分的药粒先行抵达药室右端面后，从图9(a)的速度矢量分布可看出，药室右侧会有顺时针涡流形成，在涡流的作用下，运动到药室右侧的药粒与壁面碰撞后向斜下方运动，导致药室右侧药粒堆积数增多；端盖下半部分先破孔的工况中，当药室内下半部分的药粒先行抵达药室右端面后，从图9(b)所示的速度矢量分布可看出，药室右侧会有逆时针涡流形成。在涡流的作用下，药室右侧的药粒与壁面碰撞后向斜上方运动，这部分药粒的反向运动行程变大，导致水平堆积部分的平均药粒厚度变厚，陡坡状药粒堆积占比变少。

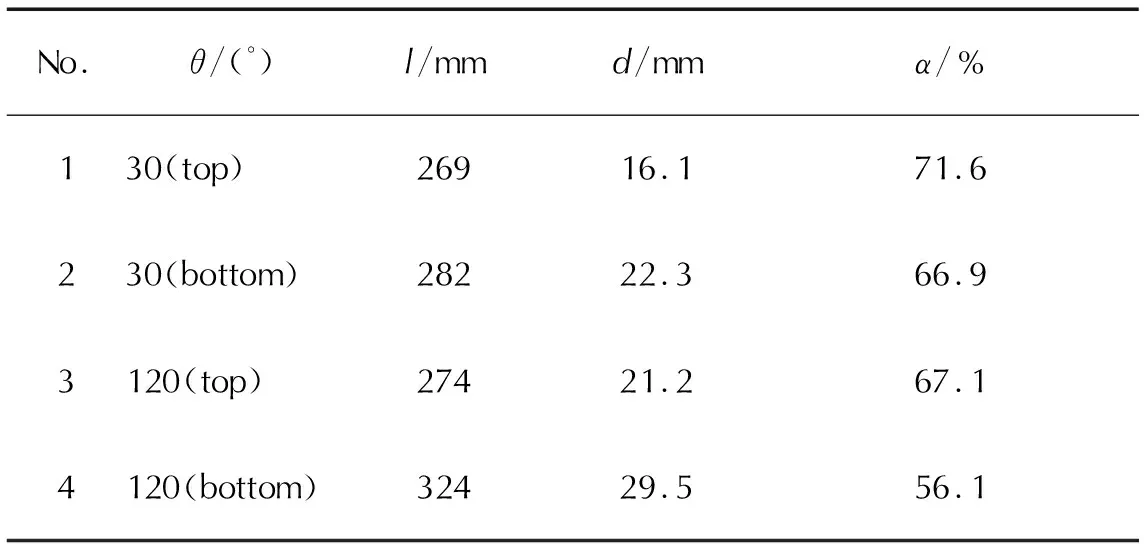
表3 药盒端盖上下破孔位置对药粒堆积形态的影响Table 3 Influence of the priority broken sector in the top/bottom of the end cap on the stacking of grains

图9 药粒碰壁后药室内流场速度矢量分布图 Fig.9 Velocity vector distribution of flow field in chamber after grain colliding with wall

3.2.2 药盒端盖左右部位先破开工况

为了探究药盒端盖先破开部分的左右分布对药粒分布特性的影响,如图10所示，分别选取端盖先行破孔的区域对应的扇形夹角θ同为60°、90°，其位置分别处于端盖的左半部区域和右半部区域4种工况进行数值模拟。 4种不同工况下药室内药粒的最终堆积状态如图11所示。

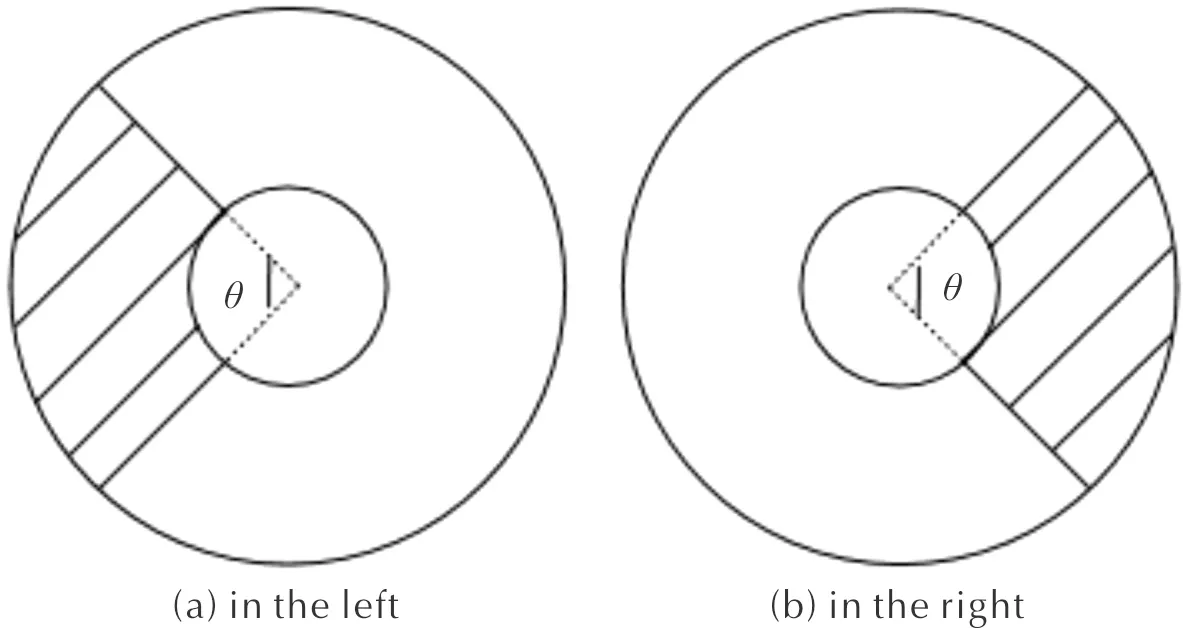
图10 端盖左右初始破孔部位示意图Fig. 10 Schematic diagram of the priority broken sector in the left and right side of the end cap

图11 端盖先破孔部分左右不同分布所对应的药粒堆积终态Fig.11 Final state of grain accumulation corresponding to different priority broken sectors in the left and right side of the end cap

为了更好地探究药盒端盖先破开部分的左右分布对药粒分布特性的影响，在引入缓坡和水平堆积的总轴向长度l、水平堆积部分的平均药粒厚度d和陡坡部分药粒堆积占比α3个特征量的同时，再引入两个特征量：陡坡堆积部分药室左右两侧的药粒数占比αc、αr，如图12所示。分别对4种工况的堆积结果进行测量，数据整理如表4所示。

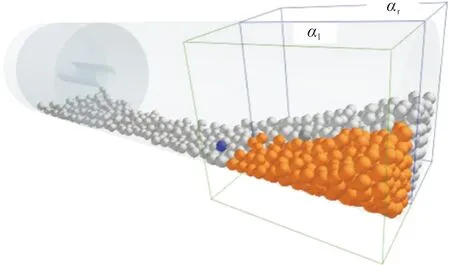
图12 陡坡堆积部分药室左右两侧划分示意图Fig.12 Schematic diagram of the division of left and right side of the steep slope accumulation section in the chamber

由表4可知，在模块药盒端盖先破开部分的大小和相对于药室高度分布相同的情况下，端盖左侧先破孔与右侧先破孔相比，缓坡和水平堆积的轴向长度、水平堆积部分的平均药粒厚度、陡坡状药粒堆积占比均基本相同，但先破孔的一侧陡坡堆积部分药粒数占比会略低于后整体打开的一侧。这是因为先破孔的一侧药粒的初始流量就更大，端盖全部打开后因流速差异，药粒彼此间相互作用，减速、停止的就会更多，运动到药室右侧陡坡部分区域的药粒数就会相对变少。但由于药室为圆柱形分布，药粒在重力作用的影响下，数量多的一侧会向数量少的一侧流动。因此，当药粒运动停止后，两侧虽仍有数量差异，但已大幅降低，先破孔的一侧陡坡堆积部分药粒数占比会略低于后整体打开的一侧。

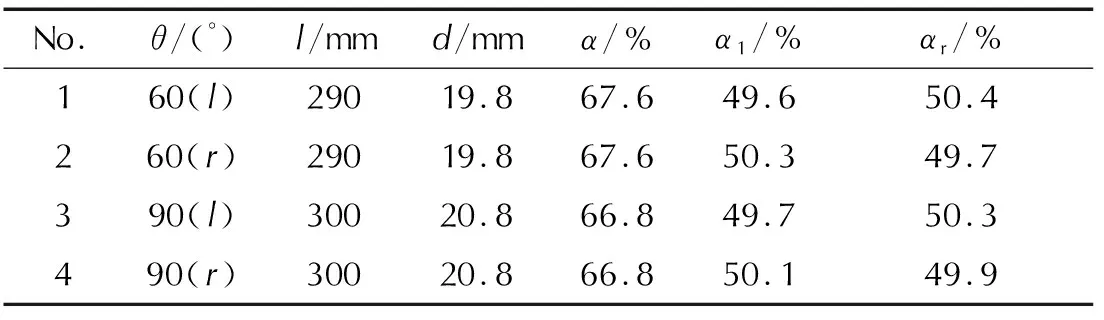
表4 药盒端盖左右破孔位置对药粒堆积形态的影响Table 4 Influence of the broken sector in the left/right of the end cap on the accumulation of grains

综上表2～表4的计算结果可知，模块盒不同的破孔方式，其药粒最终堆积形态基本一致，主要是陡坡状堆积的药粒占比数不同。从药粒的燃烧角度来看，药粒在药室内堆积分布越均匀，产生的起始压力波就越小。

4 结 论

(1)基于流固耦合方法，建立了单模块药盒点火燃烧破裂后，药盒内药粒飞散过程的三维非稳态气固两相流模型，获得了模拟发射药粒在药室内的最终堆积形态，即：依次呈缓坡堆积、水平堆积及陡坡堆积的组合分布形态。模拟结果与实验测点数据相比，平均误差为4.7%，验证了药粒散布计算模型的合理性。

(2)药盒端盖初始破孔大小会对药室内药粒的散布特性产生影响，当初始破裂区域所对应的扇形圆心角从0°增为120°时，缓坡和水平堆积的轴向长度由269mm增至320mm，水平堆积部分的平均药粒厚度由18.1mm增至22.8mm，陡坡状药粒堆积占比由70.3%减少为65.1%。

(3)药盒端盖初始破开位置也会对药室内药粒的散布特性产生影响。端盖下半部分区域较上半部分区域先破孔，缓坡和水平堆积长度更长，且平均药粒堆积厚度更厚，陡坡状药粒堆积占比更少；对比端盖左右两侧先破孔，缓坡和水平堆积的轴向长度、水平堆积部分的平均药粒厚度、陡坡状药粒堆积占比均基本相同，先破孔的一侧陡坡堆积部分药粒数占比会略低。