永磁同步电机转子偏心电磁力和挠度的分析与计算

赖文海, 黄开胜, 周 游

(1.广东省东莞电机有限公司,广东 东莞 523130；2.广东工业大学 自动化学院,广东 广州 510006；3.湖南科技大学 机电工程学院,湖南 湘潭 411100)

0 引 言

随着居民生活用电和工业用电的不断攀升，部分地区倡导工业生产错峰用电和采取拉闸限电来调整国内日益上涨的电力负荷。能源急缺的问题日益严重，合理用电和提升电器设备能效是当务之急。国家在“十三五”节能减排综合工作方案中重点强调了电机系统能效提升的节能减排工作。2020年5月，国家标准化管理委员会发布标准GB 18613—2020《电动机能效限定值及能效等级》，此标准于2021年6月强制实施。淘汰了YE2(旧三级能效)电机，YE3和YE4分别降为新三级和二级能效电机，电机产品开始进入高效节能的时代。

永磁同步电机(PMSM)具有功率密度大、高效节能、控制精准、稳定性强等优点。采用标准三相异步电机铸铁外壳的PMSM，更具有安装方便、通用性强的优点，铸铁机壳PMSM在现代工业制造中得到了广泛应用。我国大部分国企转制民营的工业异步电机生产企业具有较深厚的技术沉淀，在铸铁机壳PMSM产品上可以实现快速延伸和转型。使用铸铁机壳的PMSM产品可以实现与标准三相异步电机相同的安装尺寸，根据不同使用工况，还可以降低1～3机座号，但是在相同的机座号下提高电机的功率，转子上产生的不平衡磁拉力将会变大，并且随着PMSM产品竞争的加剧，电机定转子之间的气隙通常做得较小，相同刚度的转子在较小气隙和较大不平衡磁拉力的情况下，转子挠曲程度会变大，造成不平衡磁拉力和挠度再次变大，进而导致电机振动噪音的加大、主轴和轴承寿命降低，严重时有可能造成电机托底等问题，对电机的机械结构造成了新的考验。

文献[1]通过理论推导了分数槽集中绕组电机不平衡磁拉力的解析表达式。文献[2]通过区域法和摄动法研究计算了两极平行充磁实心圆柱式PMSM转子偏心磁场和不平衡磁拉力。文献[3-8]对转子偏心不平衡磁拉力进行理论推导和有限元法计算。文献[9]详细介绍了转子动力学的理论基础和相关计算方法。文献[10-13]通过解析计算和有限元法计算了转子挠度。但缺少对转子偏心电磁力和转子挠度有限元法计算的综合介绍与研究。

本文以目前新型节能的大功率PMSM产品为研究对象，重点研究转子偏心电磁力和挠度的准确计算方法。详细阐述转子偏心电磁力和转子挠度的理论解析和有限元计算过程，并将两种方法的计算结果进行对比，验证了所提方法的可行性和可靠性。

1 不平衡磁拉力产生的原因

造成PMSM不平衡磁拉力的主要因素可以分为电磁和机械两大类：

(1) 电磁因素。电磁设计造成的磁路不对称，如分数槽极配合、不均匀气隙、磁极偏移等。生产制造中造成的磁场不对称，比如装错磁钢、磁钢性能一致性差、绕错线圈、定子落线错误等。使用过程中造成的磁场不对称，比如供电电源不对称、高温过载造成部分磁钢退磁。

(2) 机械因素。结构设计造成的转子偏心，如没有充分考虑轴承游隙、轴承刚性变形、主轴挠度、电机气隙太小等。机械加工造成的转子偏心，这个因素主要取决于电机定子、转子、端盖和轴承的机械加工和配合的精度。装配和拆卸不当，各个零部件受力不均匀变形造成的转子偏心。轴承保养或者选用不当，轴承磨损造成的转子偏心。各个零部件质量不均匀，动平衡精度不达标等。

本文主要研究转子偏心造成的不平衡磁拉力，转子偏心结构示意图如图1所示，转子圆心和定子圆心偏心距为px，α为机械角位置，δ0为均匀气隙的长度，γ为偏心气隙角位置。

图1 转子偏心结构示意图

任意t时刻，α位置的气隙大小可以表示为

δ(α,t)=δ0+px(α-γ)

(1)

任意t时刻，α位置的气隙磁密可以表示为

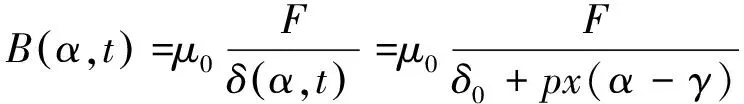
(2)

根据麦克斯韦张量法，任意t时刻，α位置的径向力密度和切向力密度可以表示为

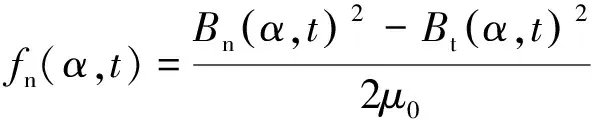
(3)

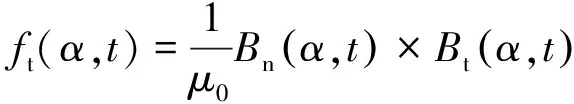
(4)

式中:μ0为真空磁导率;Bn(α,t)为径向磁密分量；Bt(α,t)为切向磁密分量。

由式(2)～式(4)可以看出，偏心转子的气隙不均匀，气隙小则磁阻小磁密大，气隙大则磁阻大磁密小，导致沿气隙圆周分布的磁密和电磁力密度发生改变以致不对称，最终将会在转子表面合成指向气隙较小一侧的不平衡电磁力。

2 不平衡磁拉力和挠度的解析计算

2.1 不平衡磁拉力的解析计算

PMSM常采用转子外圆偏心技术，使定转子间的气隙不均匀，进而可以改善转子磁场[14]，图2为不均匀气隙的内置式永磁电机(IPM)单元电机结构示意图。

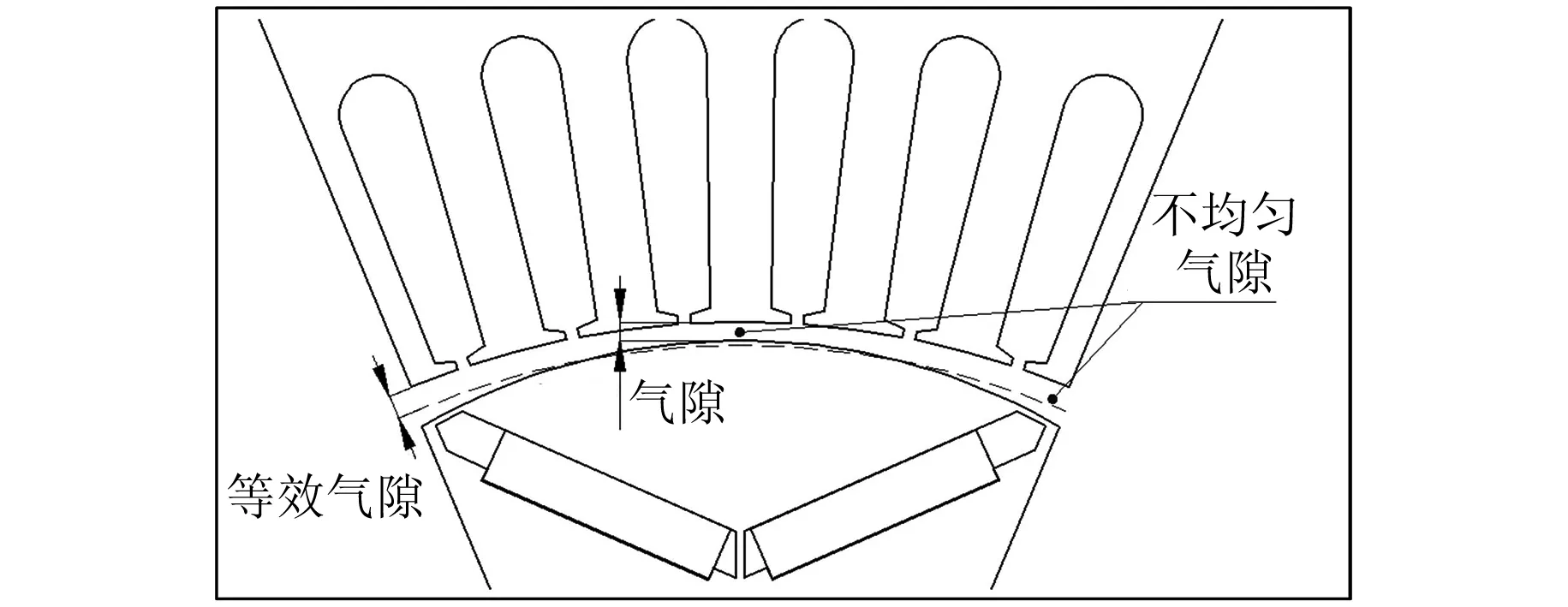
图2 不均匀气隙IPM结构示意图

本文以355 kW 1 500 r/min IPM结构的铸铁机壳PMSM为例，计算转子偏心的不平衡磁拉力和转子挠度，电机的电磁和尺寸参数如表1所示。

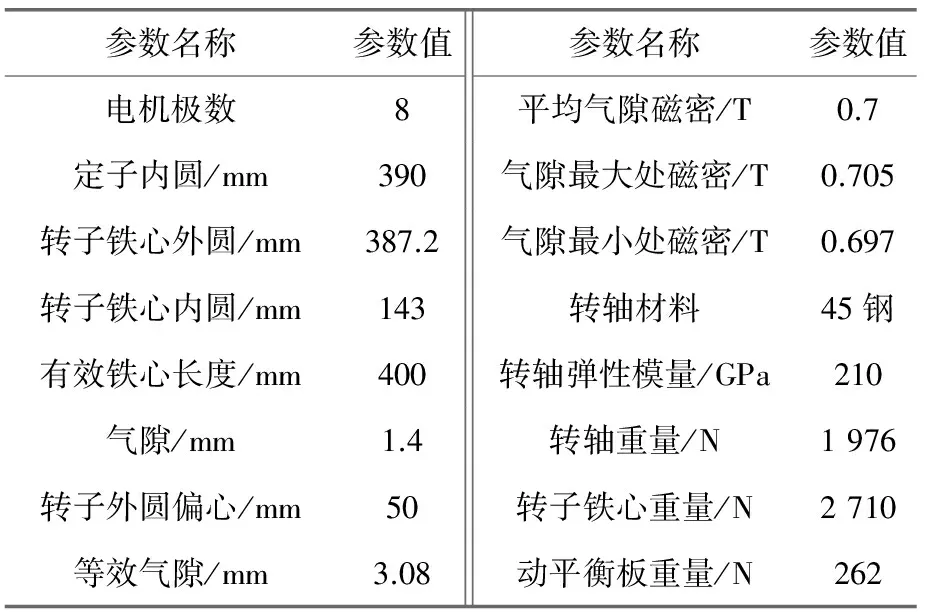
表1 电磁和尺寸参数

假设转子在垂直方向上发生偏心，考虑不同电机类型、磁场分布、磁路饱和、开槽等结构影响，可以推导出初始单边磁拉力的解析表达式[15]：

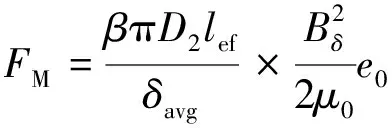
(5)

式中:β为经验系数，感应电机β=0.3，凸极同步电机、直流电机β=0.5，汽轮发电机β=0.2，此处PMSM取β=0.3；D2为转子外圆直径；lef为有效铁心长度；Bδ为平均气隙磁密；δavg为等效气隙长度；e0为初始偏心，此处取0.1δ。

文中所有公式的单位标准参考标准GB 3101—1993，根据表1参数计算得到不平衡磁拉力为1 293.6 N。

由于目前PMSM不断优化出现新的转子结构，例如转子外圆偏心、转子外圆开辅助槽、增大交直轴磁阻比设计等结构，使得式(5)中的经验系数β取值无法具有普适性。文献[10]忽略大中型高压高速电机端部效应的影响，推导了单边磁拉力的解析表达式：

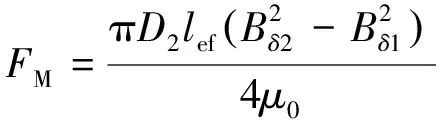
(6)

式中：Bδ2为气隙最小处磁极平均磁密；Bδ1为气隙最大处磁极平均磁密。

根据式(6)计算得到不平衡磁拉力为1 085.7 N。这种方法需要获得较为精确的最大和最小处气隙磁密来保证计算结果的准确性。针对目前PMSM转子设计越来越精细和缩短开发周期的要求，可以依靠有限元软件来计算。

2.2 转子挠度的解析计算

本文采用能量法[15]和当量直径法[16]来计算转子挠度，不平衡磁拉力采用式(5)的计算结果。将转子前后轴承简化为铰支约束，不平衡磁拉力和轴上零部件的重力简化为集中力作用，转子的简化模型如图3所示，ai、bi表示距A、B铰支的距离，i=1,2,3；G为转轴、转子铁心重力和两侧平板的重力之和；FM为不平衡磁拉力。

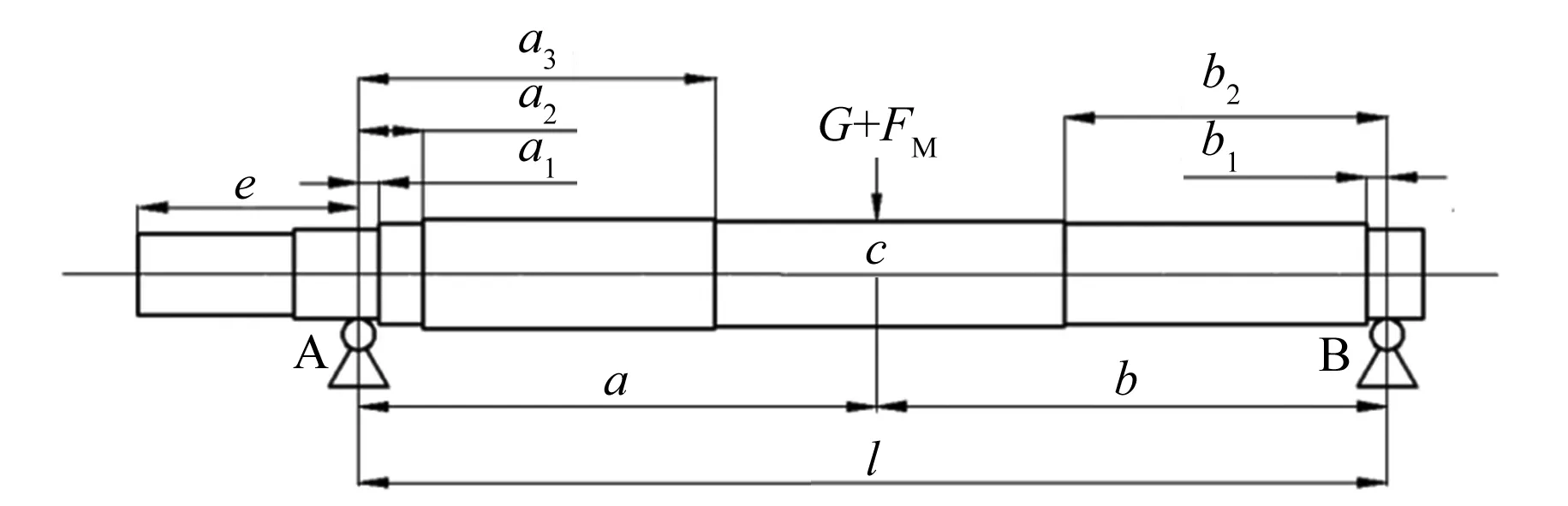
图3 转子的简化模型

2.2.1 基于能量法的挠度计算

根据材料力学，弯矩M作用在一端固定长度为l的等截面梁上,所储存的变形能为[17]

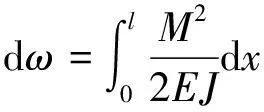
(7)

对图3变截面梁采取分段计算，a段轴内所储存的变形能为

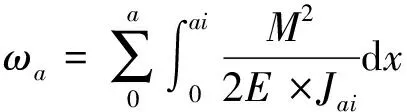
(8)

式中：E为转轴的弹性模量；Jai为铰支A侧第i段轴最大轴径的截面惯性矩。根据卡斯奇诺定理得到a段轴的假想挠度：

(9)

同理可以得到b段轴的假想挠度fb。根据几何关系可知重力G引起的挠度为

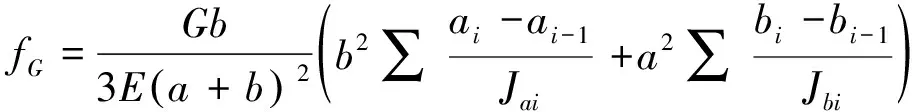
(10)

考虑不平衡磁拉力的挠度为

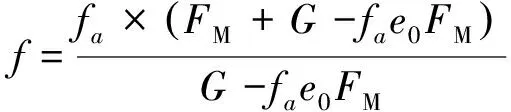
(11)

根据式(9)～式(11)以及表1和表2中的参数，可以计算得到本文案例转子的挠度。

表2 基于能量法的转子挠度计算

2.2.2 基于当量直径法的挠度计算

当量直径法是将不等截面梁等效为等截面梁的一种简化计算方法，等截面的当量直径为

(12)

将图3转轴不同直径的轴端分别分段，li表示为不同轴段的长度；di表示为各轴段直径。本案例基于当量直径法的转轴最大挠度为

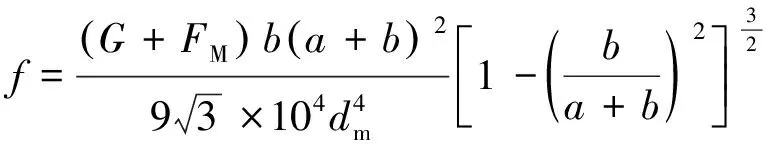
(13)

最大挠度计算结果为0.090 6 mm。

3 偏心电磁力的有限元分析与计算

目前已有较多电机振动噪声的相关研究，并且提到了采用Maxwell软件，该软件可以准确分析计算各种复杂结构电机的电磁场，特别是转子偏心的电磁力计算方面，但却缺乏相关内容的详细介绍，下面将对此进行详细阐述。

3.1 转子偏心电磁力理论

通过几何关系，可以将式(3)和式(4)转化成任意t时刻x和y方向电磁力密度：

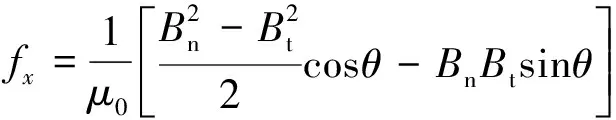
(14)

(15)

沿转子表面积分再乘以铁心长度，即可得到x和y方向以及合成电磁力：

式中：r为转子外圆半径。

Maxwell软件可以方便得到模型上任意半径r，位置角为θ的点的磁场矢量B(θ,r)，再通过几何关系可以得到径向和切向磁场分量：

Bn(θ,r)=Bx(θ,r)cosθ+By(θ,r)sinθ

(19)

Bt(θ,r)=By(θ,r)cosθ-Bx(θ,r)sinθ

(20)

由于Maxwell软件输出的磁场曲线为求解路径上n个点数值的拟合曲线，故可以将式(16)和式(17)的曲线积分计算转化为n个点电磁力的算数平均计算：

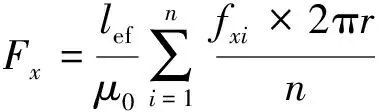
(21)

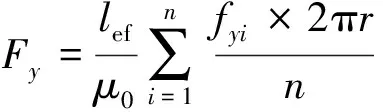
(22)

3.2 转子偏心电磁力有限元计算

方法1：根据式(18)～式(22)在Maxwell软件中创建电磁力输出项，在转子模型外圆表面绘制圆形求解路径[18]，可以通过软件求解偏心转子的电磁力。为了便于得到不同求解路径和铁心长度计算，本文讨论力密度的公式，电磁力仅需要再乘以圆形路径半径和铁心长度即可得到。电机负载时，沿转子圆周表面的fx和fy分布如图4和图5所示。

图4 x方向力密度分布

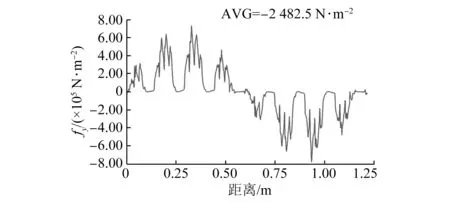
图5 y方向力密度分布

方法2：通过前面的数据可以计算得到Fx=14.1 N，Fy=1 208 N，F=1 208.1 N。此外，通过软件可以在转子模型上设置Force parameter直接计算得到Fx和Fy,根据式(18)关系，进而可以计算得到电机负载时随时间变化的不平衡磁拉力曲线如图6所示，其平均值为1 256.4 N。

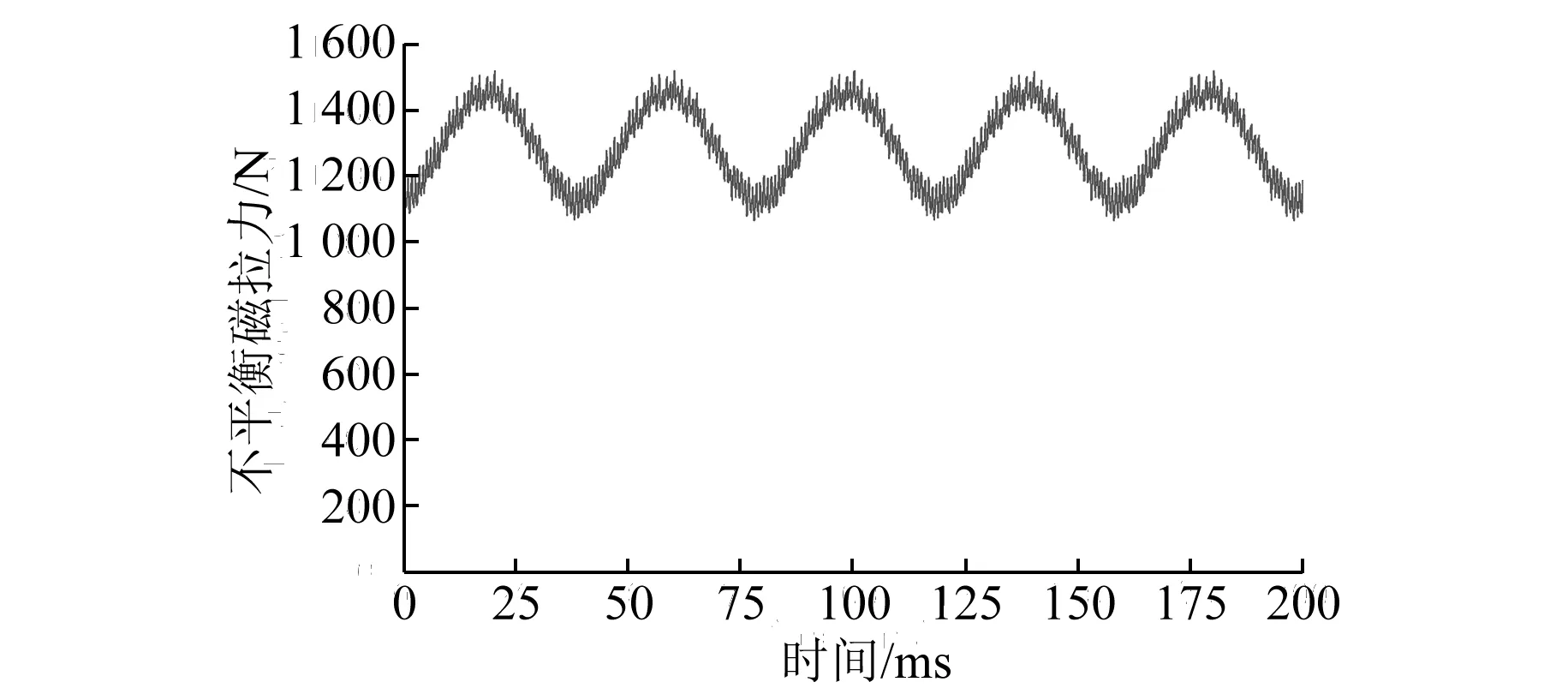
图6 不平衡磁拉力的时间变化曲线

解析法和有限元法电磁力计算结果接近，结果如表3所示。有限元方法可以充分考虑转子的复杂模型、齿槽效应、磁饱和等影响，不需要设置经验系数，计算结果更可靠。

表3 不平衡磁拉力结果对比

4 转子挠度的有限元分析与计算

下文主要介绍转子挠度有限元计算过程中转子模型的简化，负载及约束的施加。

4.1 转子模型简化

转子挠度静力学分析常采用三维有限元计算。转子铁心由一定数量的矽钢片叠压而成，PMSM的转子铁心常采用铆钉、自扣槽、螺杆、螺母等方式紧固，转子模型如图7所示。

图7 转子模型

在转子受力挠曲时，矽钢片之间的挤压摩擦，以及磁钢、铆钉、螺杆的嵌套会减小主轴的挠曲，但影响有限。另外，因为实际转子铁心的三维模型很复杂，有限元的计算量过于庞大，计算机容易出现内存溢出，所以转子铁心、磁钢简化为对主轴的重力作用。

动平衡板与主轴过盈配合可以增大所在轴段的截面惯性矩，提高抗弯能力，但两端的动平衡板轴向尺寸较小，因此本文忽略动平衡板模型，将其简化成动平衡板对主轴的重力作用。

轴承可以简化成等效的铰支约束，最终可以将图7模型简化为只有转轴与载荷和约束的模型。

4.2 载荷和约束的施加

为了便于施加载荷和约束，需要将转轴分割出轴承和铁心轴段位，如图8所示，并且在软件中把分段模型合成一个整体。

图8 转子分段示意图

在图8铁心段y负方向上施加不平衡磁拉力1 208.1 N，再叠加上转子铁心、动平衡板和磁钢的重力2 972 N，最后对转轴模型y负方向上赋予重力加速度完成载荷施加。

施加约束时需要分析实际模型的空间自由度。本文所述转子采用深沟球轴承，在后轴承外圈采用波形弹簧对转子轴向方向进行预紧，故可以将前、后轴承作用分别近似等效为固定铰支(自由度为3个正交轴向转动)和可动铰支约束(自由度为3个正交轴向转动和1个轴向平动)。

4.3 挠度计算结果

计算结果如图9和图10所示，图9中转轴的y方向的变形量用灰度图体现，变形量越大颜色越深。图10为沿轴中心线，转子在y方向的挠度分布，转轴挠度最大发生在距离轴伸前端面1 000 mm处，最大挠度为0.092 6 mm。

图9 转子挠度灰度图

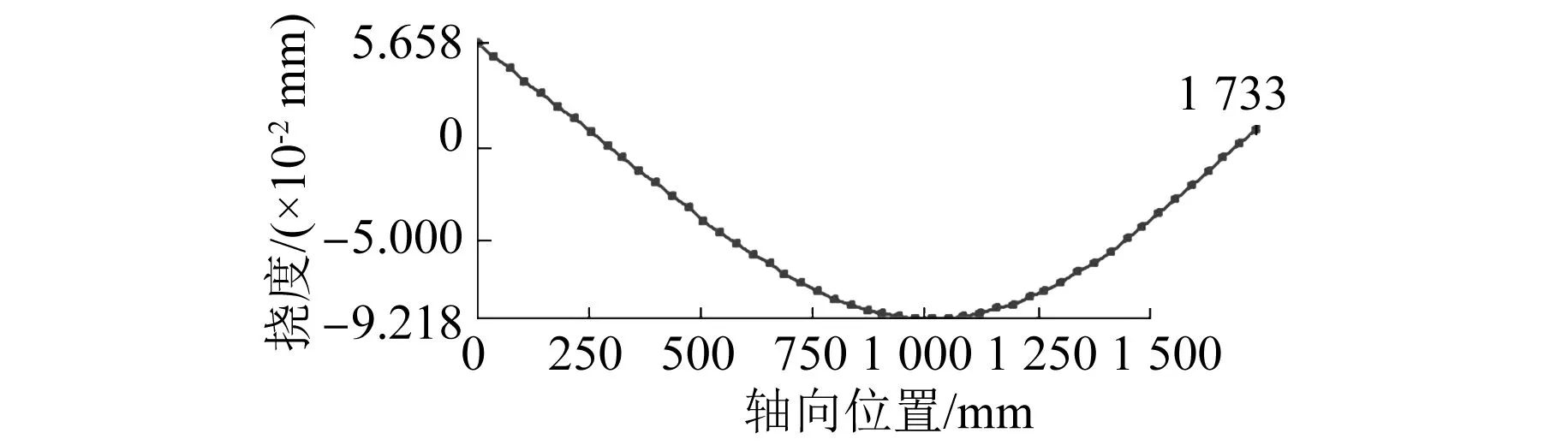
图10 转子挠度分布图

5 计算结果对比

有限元挠度计算值0.092 6 mm是使用不平衡磁拉力有限元计算值1 208.1 N代入计算的结果，将该不平衡磁拉力有限元计算结果代入能量法以后的挠度值为0.099 4 mm，代入当量直径法以后的挠度值为0.089 4 mm，三种方法的计算结果接近，验证了转子挠度有限元计算方法的可靠性。

有限元计算的转子挠度占电机气隙的6.6%，根据经验，PMSM转子挠度不超过电机气隙的8%可以保证安全可靠运行。测试的电机振动值符合国家标准GB/T 10068—2020中机械振动限值要求。

6 结 语

本文以新型节能产品355 kW 1 500 r/min铸铁机壳PMSM为例，推导得到PMSM不平衡磁拉力的解析表达式，解析表达式适当转化以后，便于将不平衡磁拉力公式输入到Maxwell软件并求解。本文详细介绍了转子不平衡磁拉力和挠度的有限元分析计算方法，通过对比解析计算方法和结果，验证了所提方法的可行性和可靠性，有限元方法可以考虑各种复杂模型、磁场饱和影响，不需要设置经验系数，尤其是对转子结构较为复杂的PMSM，所提出的有限元方法计算结果更可靠。