分数槽集中绕组定子磁动势的分解

陈会崇, 宋承林

(青岛中加特电气股份有限公司，山东 青岛 266400)

0 引 言

一般交流电机定子绕组的每极每相槽数q为大于1的整数，节距y略小于每极槽数，称之为分布短距绕组。而分数槽集中绕组的每极每相槽数是分数且q<1，线圈的两条边放置在相邻的槽内即y=1。由此可知分数槽集中绕组的特点有：极对数p一定时，定子槽数Q成倍减少，结构简单，铁心模具容易加工；线圈数量少，且相互没有交叉重叠，端部长度较短，用铜量及铜耗少，方便采用自动嵌线工艺[1-2]。

近10年来，分数槽集中绕组在永磁同步电动机、永磁无刷电动机、同步磁阻电机[3]和直线电机[4]中得到了越来越广泛的应用。如小型的外转子通风机电机和机器人用伺服电机[5]因定子空间小，槽数不宜过多；低速大转矩直驱电机的额定转速小于100 r/min，需采用较多的极对数,采用分数槽集中绕组已成这类电机的主流方案。与分布短距绕组的极对数较直观不同，分数槽集中绕组的极对数与转子有关。而作为交流电机电磁转矩不等于零的一个准则，定、转子极对数必须相等[6]。本文意从不同的角度解释这一现象，并为研究新的分数槽集中绕组提供一种思路。本文分解磁动势的方法分为两种:交流电的绕组理论和函数的傅里叶级数展开。

1 单元电机简介

当定子槽数Q与极对数p的最大公约数t不为1时，可以把整个绕组分成t个完全相同的单元，每一单元有p/t对极和Q/t个槽。由于各个单元的相应槽号在磁场中所处的位置完全相同，所以只需研究一个单元内的定子磁动势即可。如研究27槽24极的电机，可简化为研究9槽8极。而在低速大转矩场合广泛应用的48槽40极、72槽60极、96槽80极等电机，定、转子的磁场分布与12槽10极的电机等效，可一并研究。

现以12槽双层集中绕组为例说明。双层绕组的线圈数等于槽数，每相有12/3=4个线圈。为充分利用集中绕组的特点获得较高的电动势，需要2个线圈作为一组相邻，且电流方向相反；为使每相绕组的磁动势在空间均匀分布，需要2组线圈空间相差180°；因2组线圈对应的转子极性不同，故电流方向应相反。综上所述，12槽双层集中绕组接成一路串联时一相的接线方式如图1所示。

图1 12槽双层集中绕组一相展开图

为简化分析，这里假设：

(1) 忽略定、转子铁心的的磁压降，不考虑饱和，磁动势全部作用在气隙上，且交链定、转子，没有漏磁；

(2) 气隙均匀，不考虑永磁体的作用，d轴和q轴的磁导相等。

2 交流电机的绕组理论

2.1 单个线圈的磁动势

N匝整距线圈通入交流电流，有效值为I，根据《电机学》绕组理论可知，ν次空间谐波磁动势幅值

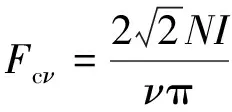
(1)

因为单元电机的定子槽数与转子极对数的最大公约数为1，故可忽略转子极对数，从结构上认为定子绕组为“2极”，整距线圈的“节距”，即“极距”τ=Q/2=6。

集中绕组的节距y=1，单个线圈的基波节距因数:

(2)

单个线圈ν次谐波的节距因数

(3)

2.2 一组线圈的磁动势

一组线圈有两个线圈，等效后的每极每相槽数q=2。图1中两线圈距离为1个槽，等效后的“机械角度”为π/6，但因电流方向相反，故“电角度”α=5π/6。

线圈组的基波分布因数：

(4)

线圈组ν次谐波的分布因数：

(5)

于是，线圈组的磁动势：

(6)

式中:Nt为线圈组的串联总匝数，Nt=2N；kwν为线圈组ν次谐波的绕组因数，等于该次谐波节距因数与分布因数之积，即：

kwv=kpvkdv

(7)

可以根据式(3)、式(5)和式(7)计算绕圈组的绕组因数。基波到20次谐波的绕组因数如表1所示。

表1中出现的负号是指该因数引起的某次谐波的磁动势与基波磁动势方向相反。

通过表1可以得到以下结论：

表1 12槽集中绕组一组线圈的绕组因数

(1) 次数相差12的谐波，绕组因数相等，即kν=kν+12。绕组因数以12为周期出现，这是因为定子槽数是12。

(2) 一个周期内，半周期处和全周期处的绕组因数为零，即若m为任意自然数，k12m-6=k12m=0。另外，其他关于6对称次谐波的绕组因数相等，即若n为小于6的自然数，k6m-n=k6m+n。

(3) 一个周期内，半周期处两侧的绕组因数最大，达0.933，说明该次谐波的利用率较高；其他次数谐波的绕组因数最高为0.5，几乎没有利用价值。

2.3 一相绕组的磁动势

12槽集中绕组中的一相绕组包含4个线圈，即2个线圈组。这样一相绕组产生的磁动势是一个线圈组的2倍。但需注意，因为2个绕圈组在空间相差电角度为π，故相磁动势不包括偶次谐波。

根据交流电机的绕组理论，线圈组产生的磁动势只与槽内电流方向有关，而与其接法无关。所以一相的8个线圈边可以看作4个整距线圈，如图2所示。而整距线圈所生的为一系列奇次谐波磁动势。

图2 一相集中绕组线圈等效成整距线圈

这样，一相绕组所生的ν次谐波磁动势幅值

(8)

式中:Nw为线圈组的串联总匝数，此处Nw=4N。

2.4 三相绕组的合成磁动势

通入正弦交流电流时一相绕组产生的是一系列奇数次波的脉振磁动势。三相绕组轴线空间上均匀分布，互差2π/3电角度；三相电流频率相同，时间上亦互差2π/3电角度。定义A相绕组的轴线为空间原点，A相电流由负变正时为时间原点，那么时间t处距离A相绕组轴线为α角度处A、B、C三相产生的ν次谐波磁动势：

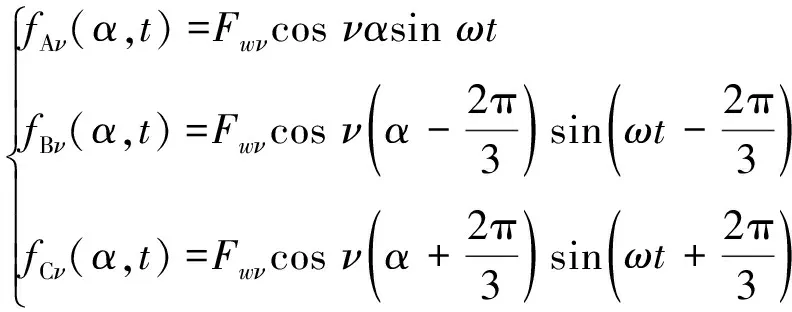
(9)

式中:ω为电流变化的角速度。

此时此处的三相合成磁动势为

fν(α,t)=fAν(α,t)+fBν(α,t)+fCν(α,t)

(10)

将式(9)进行三角函数的积化和差，代入式(10)，并经处理后可得到以下结论：

(1) 3以及3的倍数次谐波磁动势为0，即单元电机中不存在3及3的倍数次谐波；

(2) 当ν=6i+1(i=0，1，2，…)时，fν为

fν=1.5Fwvcos(ωt-να)

(11)

基波及谐波合成磁动势为正向旋转,转速为120πω/ν,幅值为1.5Fwν；

(3) 当ν=6i-1(i=1，2，3，…)时，fν为

fν=1.5Fwvcos(ωt+να)

(12)

谐波合成磁动势为反向旋转，转速为120πω/ν，幅值为1.5Fwν。

考虑到基波和各次谐波的绕组因数，经计算可知5次谐波的磁动势幅值最大。50次以内基波和各次谐波磁动势幅值与5次谐波磁动势幅值之比如图3所示。

图3 12槽集中绕组各次谐波相对值

3 函数的傅里叶级数展开

3.1 单个线圈通电产生的磁动势

N匝线圈通入电流i，当电流方向为下进上出时，线圈内的磁力线从左向右穿过气隙，如图4所示。

图4 单个线圈产生磁通的磁力线

线圈内气隙面积与线圈外气隙面积之比为1…11，根据磁路的磁阻R=L/(μ0S)，线圈内气隙的磁阻与线圈外气隙的磁阻之比为11…1。由于流入线圈内气隙的磁通等于流出线圈外气隙的磁通，根据磁路的欧姆定律F=RΦ，线圈内气隙的磁压降是线圈外气隙的11倍。以线圈轴线为原点，沿气隙方向展开，得到线圈产生磁动势的分布图，如图5所示。

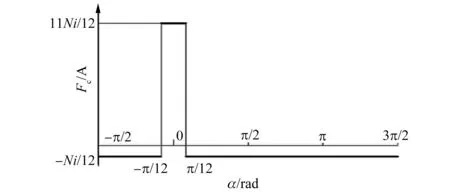
图5 单个线圈的磁动势

3.2 用傅里叶级数分解整距线圈磁动势

若周期函数f(x)满足一定的条件[7]，且周期是2π，在[-π,π]内，函数用傅里叶级数可表示为

(13)

当函数f(x)已知时，可以求出：

(14)

(15)

(16)

式中:n=1,2,3，…。

把求得的a0，an，bn代入式(13)即可得到f(x)的傅里叶级数表达式。

傅里叶级数在电工学中有较广泛的应用。把线圈或绕组的磁动势按傅里叶级数的形式写出的物理意义是：空间上的矩形波可以分解为幅值不等、周期从一到无穷大的一系列正弦(或余弦)波。

整距线圈在两侧气隙生成的磁动势数值相等，为总磁动势的1/2；以线圈轴线为坐标原点，沿转子外径展开，得到圆周上不同位置磁动势的相对值:

(17)

计算a0，an，bn:

(18)

解得,当n=0时，a0=0；当n=1,2,3,…时,an为

(19)

bn=0。

实际上，函数中的n就是磁动势分析中的谐波次数ν。以上结果表明：

(1) 磁动势在横坐标轴上方和下方的面积相等，所以级数的常数项a0/2=0；

(2) 因为把线圈轴线当作了纵轴，原函数是偶函数，故级数没有正弦分量，bn=0。后续将尽可能把函数设为偶函数，不再计算bn。

(3) 关注an。当n为偶数时，an=0，这就是绕组理论中强调的整距线圈没有偶数次谐波；当n=4i+1(i=0,1,2,…)时，an>0，说明x=0时(线圈轴线位置)n次谐波的波峰与函数值同向；当n=4i-1(i=1,2,3,…)时，an<0，说明x=0时n次谐波的波峰与函数值同反向。

综上，整距线圈磁动势(与总磁动势的相对值)的傅里叶级数表达式为

-π≤x<π

(20)

绘制原波形和分解后的前4项谐波图像如图6所示。

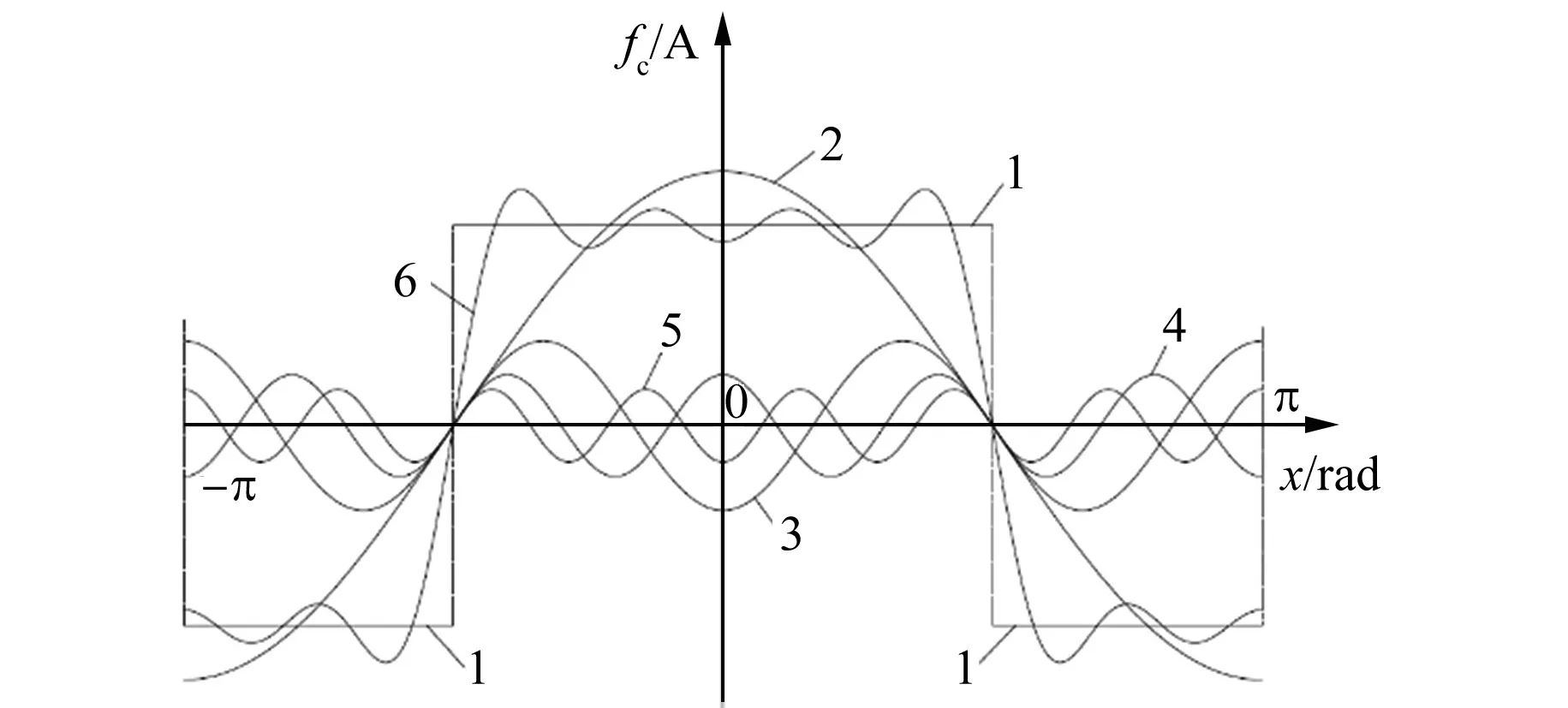
图6 整距线圈的磁动势分解

图6中，曲线1为分解前矩形波磁动势；曲线2、3、4、5分别为基波、3次、5次、7次谐波磁动势；曲线6为曲线2～曲线5的叠加。可以看出，曲线6和曲线1接近。

3.3 分解集中绕组线圈磁动势

按3.1节所述，写出图4表示的磁动势相对值的表达式：

(21)

根据上文分析，只计算an即可。解得：

(22)

磁动势相对值的傅里叶级数表达式：

-π≤x<π

(23)

式(23)表明：

(1) 集中绕组磁动势既包含奇数次谐波，也包含偶数次谐波；

(2) 奇数次谐波的幅值与整距线圈比较，多出一个系数sin(nπ/12)，这就是线圈的节距因数kpν(习惯上用ν代替n)。

实际上，本节的分析适用于所有的短距线圈。绘制原波形和分解后的前4项谐波图像如图7所示。

图7 集中绕组线圈的磁动势分解

图7中，曲线1为分解前矩形波磁动势；曲线2、3、4、5分别为基波、2次、3次、4次谐波磁动势；曲线6为曲线2～曲线5的叠加。

3.4 一相集中绕组线圈的磁动势

限于篇幅，这里不再推导一个线圈组的磁动势。总之与单个线圈比较，前面的系数是绕组因数，是线圈短距和线圈组分布的综合影响。现直接写出一相绕组一个周期内的磁动势相对值表达式:

(24)

按傅里叶级数形式写出:

-π≤x<π

(25)

可以看出:

(1) 当n为奇数时，sin(nπ/3)和sin(2nπ/3)数值相等。一相绕组的绕组因数为[sin(nπ/2)- sin(nπ/3)]/2；

(2) 当n为偶数时，sin(nπ/3)和sin(2nπ/3)数值相反，an=0，即磁动势为0。

矩形波和分解后的前4项谐波图像如图8所示，各曲线的说明同图6。

图8 一相集中绕组的磁动势分解

三相合成的磁动势见2.4节，不再赘述。

4 分数槽集中绕组的一般规律

如前所述，采用12槽集中绕组的电机，5次和7次谐波的磁动势幅值最大，所以12槽的电机通常是5对极或7对极的。可以利用5次谐波选用5对极的转子，也可以利用7次谐波选用7对极的转子，注意电源相序相同时两种电机的转向相反。如选用5次谐波，那么7次谐波就是幅值最大、扰动最强的谐波，反之亦然。所以为使电机的性能最优，极对数通常要接近但不等于定子槽数的一半。进一步总结，分数槽集中绕组的特点与槽数有密切的关系。

4.1 定子槽数和绕组因数

为使三相电机每相产生的磁动势均布，定子槽数Q必须是3的整数倍。

分数槽集中绕组中一个线圈的节矩因数为

(26)

由于电角度α=(1-2/Q)/π，代入分布因数的计算公式可知其与q和Q有关(与整数槽绕组不同)，其分布因数为

(27)

实际上，式(26)、式(27)是式(3)、式(5)的推广。绕组因数的计算见式(7)。

4.2 定子槽数是偶数

为使用幅值最大、绕组因数最高的谐波，电机的极对数p与定子槽数的关系为

p=Q/2±1

(28)

定子可以使用单层绕组，但受限较多，如采用双层绕组，每相可有空间上对称、电流方向相反的两组线圈，前面已经分析了产生的磁动势不含偶数次谐波。又因为两组线圈的相位重合，所以它们之间既可以串联，也可以并联，即并联路数可选1和2。但因为单元电机内绕组只能等效成2极，所以最多只能有两组线圈，并联路数不会大于2。

4.3 定子槽数是奇数

为使用幅值最大、绕组因数最高的谐波，电机的极对数p与定子槽数的关系为

p=(Q±1)/2

(29)

但是因为槽数是奇数，只能采用双层绕组，且线圈数等于槽数，也是奇数。这样在常用的三相电机中，每相线圈数也是奇数。所以此时一相绕组的并联路数只能为1路。每相线圈无法等效为整距线圈，故其磁动势分解后既有奇数次谐波，也有偶数次谐波。

5 结 语

虽然分数槽集中绕组的单元电机中定子槽数和转子极对数可以有若干种组合[8]，当选用的极对数接近但不等于定子槽数的一半，且槽数不太少时(如大于9)，极对数与槽数的最小公倍数足够大，这样定子齿谐波较小，改善了气隙磁场波形，所以大大降低了电机的转矩波动。这也是分数槽集中绕组的优点之一。

与以基波作用的磁场作为电枢磁场参与能量转换不同，分数槽集中绕组产生的磁场较为复杂。所以如果抛开转子，在不知电机极数的情况下，称该定子为“分数槽”，是有歧义的。因为定子转子的极对数必须相等，所以原则上可以说，只要磁动势分解后包含与转子极对数对应的谐波，电机就可以运行，即参与工作的磁动势谐波次数就是定子的极对数。为了最大程度地利用定子磁动势，需要选择合适的转子极对数与定子槽数匹配。