异步电机低速电制动控制

刘梦琪, 曲诗健, 李鹤群

(1.中车大连机车车辆有限公司，辽宁 大连 116000；2.中车大连电力牵引研发中心有限公司，辽宁 大连 116000)

0 引 言

随着信号ATO控车、无人驾驶技术的普及，地铁列车车辆控制性能要求日益增高，尤其在列车到站停车过程中，需要与屏蔽门对齐方便乘客上下车，通常要求误差不超过±50 mm。地铁列车停车制动主要采用电制动和空气制动混合控制，制动过程中当车辆速度低于设定速度点后，电制动开始退出，空气制动逐渐施加，最终由空气制动满足整车制动力需求。空气制动过程中，由于空气制动无法对制动力进行精确控制，响应时间无法保证，同时闸瓦与制动盘摩擦会产生粉尘及噪声，而由牵引逆变器控制的电制动，可以根据车辆给定直接进行准确控制，整个制动过程中，不存在电、空转换，车辆冲击小，制动能量可以回馈电网，同时没有闸瓦的损耗，不会产生粉尘和噪声[1-4]。综上，全电制动控制在制动力精确性、响应速度、材料损耗等方面存在优势，在地铁列车上应用具有重要意义和发展前景。

但是，在大功率异步电机实际应用过程中，尤其在低速时，受逆变器非线性、数字离散控制延时以及电机参数变化等因素影响，异步电机控制性能会出现明显下降，电流产生畸变，转矩发生振荡乃至控制发散。针对此问题，国内外文献主要从电机定转子参数辨识[5-7]、逆变器非线性[8-9]、电机控制策略[10-12]等方面进行改进优化。以上解决方案，在不同程度上使控制算法更加复杂且不稳定。因此，在实际工程应用中，需要一种简单、可靠的算法来提高低速下电制动性能，本文采用基于无功功率模型的转子时间常数自适应控制的方法可以有效解决低速区电制动转矩不稳定、控制精度低等问题。

1 异步电机电制动控制策略

全电制动基于异步电机矢量控制实现。异步电机矢量控制通过模型解耦，分别控制定子电流转矩分量和励磁分量，以达到类直流电机的控制效果。采用同步旋转坐标系，令d轴与转子磁链方向重合，可得电机电压方程为[13]

通过电压前馈补偿消除电压方程中由电机反电动势引起的交叉耦合项，把耦合系统改造成单变量线性系统，进而转子磁通可以通过d轴电压控制，电磁转矩可以通过q轴电压控制。在电制动过程中，车速从高速到零的过程中，在高速区电机工作在再生制动或电阻制动状态，接近零速时电机会处于反接制动状态。在再生制动或电阻制动状态，牵引逆变器始终保持输出负转差率，定子频率随转子频率降低，产生制动转矩；随着转速进一步降低，定子频率接近零，牵引逆变器定子频率过零，定子电流换向，电机处于反接制动状态，直至车辆停车。理论情况下，假设电机参数准确，逆变器采用转子磁场定向矢量控制，转子磁场位置可以准确定向，电机定子的励磁分量和转矩分量可以完全解耦，转矩可以准确控制保持稳定。

2 实际应用中低速电制动转矩偏差分析

实际应用中，异步电机参数易受温度、运行频率、磁场饱和程度、运行工况、涡流效应等外界因素影响而变化[14]。

同时，在PWM调制过程中为避免逆变器上下桥臂发生直通，通常插入死区时间。该时间与逆变器的开断延迟、开关管和导通二极管的压降是构成死区效应的三个因素。虽然插入的死区时间是由微处理器可控的，可以精确获取，并与误差电压呈线性关系，但逆变器的开通关断延迟和导通压降随着工作环境(例如,母线电压、相电流、工作频率和电机运转速度等)改变而改变，是非线性的。由于死区效应，每一个调制周期内引起的微小畸变经积累后，必然会使逆变器的输出电压非线性误差加大[8]。

在以上因素的综合作用下，转子磁场定向出现偏差，进而影响定子电流励磁分量和转矩分量解耦，使电机处于过励磁或欠励磁状态，引起电机发热，导致稳态输出性能恶化，实际表现为电机输出转矩不准、转矩产生脉动，严重会导致电机控制不稳定，车辆无法正常运行。

转子磁场定向和转子磁场存在角度偏差，如图1所示。当转子磁场定向超前滞后于实际转子磁场时，在电流控制器的调节下，可以使定子电流励磁、转矩分量按照指令值分配，电机定子电流幅值保持不变，由于定向角度的偏差，使得作用在真实d、q坐标系的定子电流励磁、转矩分量与给定值出现误差。在再生制动状态下，观测转子磁场超前于真实转子磁场，真实电流励磁电流大于指令值，真实转矩电流小于指令值；观测转子磁场滞后于真实转子磁场，真实励磁电流小于指令值，真实转矩电流大于指令值。在反接制动状态下，影响规律与再生制动相反。

图1 转子磁链定向误差示意图

取电流矢量在第四象限内，考虑电流矢量与转子磁链角度为[-60°,-70°]，根据实际数据分析，定向误差通常在[-10°,10°]，电机电磁转矩为[13]

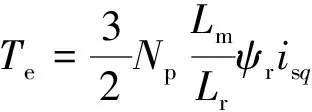
(5)

通过MATLAB可以绘制出三维空间下，给定转矩与实际转矩的比例关系，如图2所示，在再生制动状态下，观测转子磁场超前于真实转子磁场时，转矩偏小；反之偏大。在反接制动状态下，规律相反。

图2 转子磁链误差与转矩关系

3 低速下转子磁链定向校正算法

因此，在逆变器非线性因素和实际电机定转子参数不准的影响下，磁链观测器在低速下很难准确观测，此时使用基于转子磁链q轴分量的传统方法进行校正将进一步恶化磁链定向准确性。

异步电机的无功功率主要表现为储藏在电机磁场中的能量，通过无功功率的不同数学模型，可以分别作为自适应控制的参考模型和可调模型[15]。异步电机转子磁场定向dq轴系下的稳态等效电路如图3所示。

图3 异步电机转子磁场定向稳态等效电路图

定义无功功率为Q=is⊗Er，由等效电路图，参考无功功率可以表示为

(6)

同时，实际无功功率为

Q=is⊗Er=is⊗(us-σLsJωeis)=

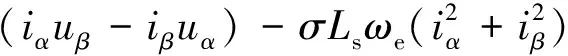
(7)

图4为基于无功功率模型的转子时间常数自适应控制，将参考无功功率和实际无功功率做比较，两者差值通过PI调整作用于参考转子时间常数，从而影响转差角频率。转差角频率的变化带来电机内部电流工作点的变化，从而影响两个无功功率的计算值，当两者达到平衡时，两个坐标轴系重合，参考转子时间常数等于实际值。

图4 基于无功功率模型的转子时间常数自适应控制

由图5和图6可以看出，参考坐标系滞后于实际坐标系，实际转子磁链幅值大于给定值，从而实际反电动势Er也偏大，参考无功功率小于实际无功功率，则PI的输入为负，使参考转子时间常数减小。参考坐标系超前于实际坐标系，实际转子磁链幅值小于给定值，从而实际反电动势Er偏小，参考无功功率大于实际无功功率，则PI的输入为正，使参考转子时间常数增大。

图5 基于无功功率模型的矢量定向示意图(参考坐标系滞后于实际坐标系)

图6 基于无功功率模型的矢量定向示意图(参考坐标系超前于实际坐标系)

此种基于无功功率模型的转子时间常数自适应控制不需要转子磁链信息，所以该方法对电机参数具有较好的鲁棒性，相对于基于q轴磁链定向的自适应控制具有一定优势。

4 试验验证

为了进一步验证低速下转子磁链定向校正算法的有效性，搭建低速制动试验台，如图7所示。试验台主要由被试电机、陪试电机、减速机、牵引逆变器、陪试变频器、制动电阻构成，被试电机采用地铁车辆中使用电机，具体参数如表1所示。

图7 低速电制动大功率试验台

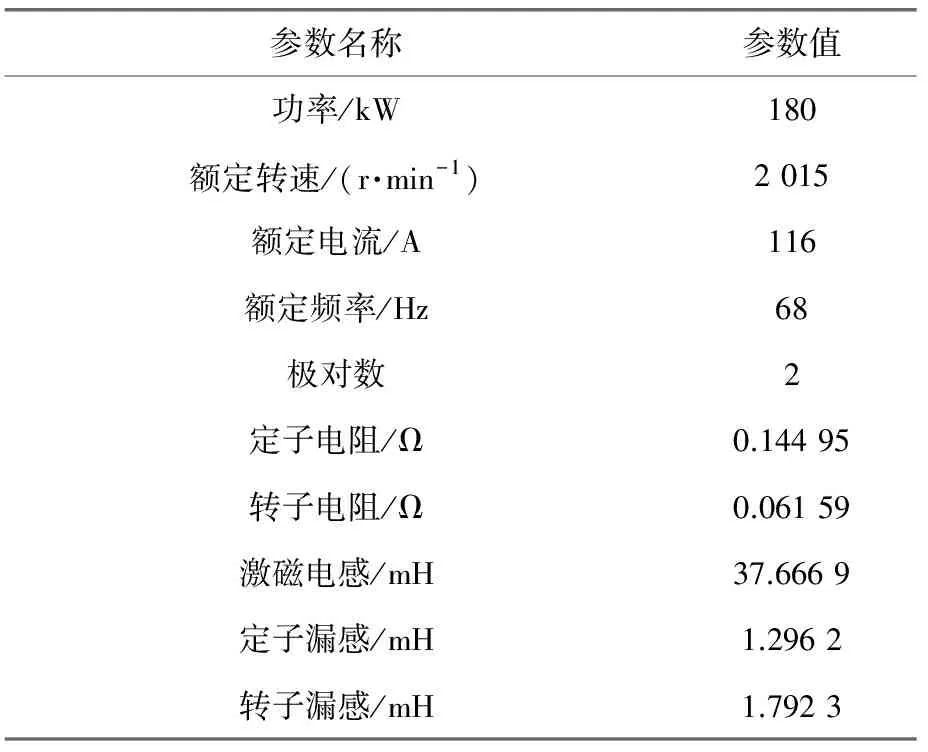
表1 被试电机参数

试验中，分别在低速12 r/min进行100%转矩试验和在低速100～12 r/min区间进行100%转矩扫频试验，波形如图8和图9所示，电机转差频率随制动转矩增大往负向增加，电机电频率穿越过零点下降变为负，整个过程中电机控制id、iq跟随给定值，制动转矩与给定转矩误差在5%内。

图8 低速制动12 r/min 100%转矩波形

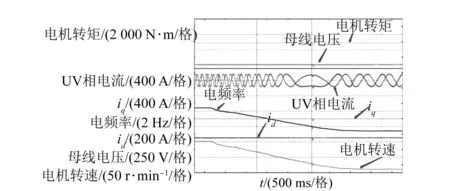
图9 低速制动100～12 r/min 100%转矩扫频波形

最后，在同样试验条件下，分别对采用基于无功功率模型的转子时间常数自适应控制算法、无转子磁链定向校正控制算法、传统转子q轴磁链定向校正控制算法进行低速制动负载扫频对比试验，具体转矩记录见图10。在整个动态过程中，采用基于无功功率模型的转子时间常数自适应控制算法在转矩的稳定性和精度上均更为优秀，电机转矩波动在±5%以内；无转子磁链定向校正控制算法由于无法对转子磁链角度进行修正，在低速制动过程中电机转矩始终存在-10%左右的误差，在20 r/min处误差达到-24%；传统转子q轴磁链定向校正控制算法受低速时磁链观测性能下降的影响，随着转速降低，电机转矩出现巨大波动，最大达-63%。经过对比试验，进一步证明在大功率异步电机低速制动过程中，本文采用的控制算法具有更好的转矩控制性能。

图10 各控制算法电机转矩

5 结 语

本文对异步电机全电制动控制原理进行说明，分析了中低速电制动转矩偏差的产生原因，提出了低速下利用无功功率模型进行磁场定向角度校正的算法。通过地面大功率试验台，验证了该算法在稳态和动态过程中可以完全实现转矩给定，误差在5%范围内。全电制动异步电机控制策略算法理论具有可行性和可靠性，在地铁列车上应用具有良好的前景。