基于PCA和改进SVDD的异常检测算法

赖思银

(广东石油化工学院，广东，茂名 525000)

0 引言

异常检测(anomaly detection, AD)是数据挖掘领域中的一个重要研究方向，其目的是从模式类或数据集中自动识别出与预期不符的异常模式或有别于大部分数据的异常数据。在工业入侵检测、银行欺诈、故障缺陷检测、医疗系统健康监测等领域中得到了广泛应用[1]。

目前，常用的异常检测方法可以分为基于统计的方法、基于邻近度的方法和基于分类的方法3大类。其中，基于统计的方法认为数据集服从某种确定的分布(如高斯分布、均匀分布等)或者概率模型，通过判断特定数据点是否符合该分布或概率模型从而实现异常数据的检测。文献[2]利用直方图的方式对数据集进行统计分析，根据未知数据是否分布在直方图中实现异常检测判断。基于邻近度的方法根据度量指标的差异又可以分为基于距离的异常检测方法[3]和基于密度的异常检测方法[4]。其中，基于距离的方法以K-最近邻(K-nearest neighbor, KNN)为代表[5]，作为一种无监督方法，该类方法无需考虑数据的分布特性，适用于高维数据的异常检测，但是由于需要计算任意2个数据点之间的距离，该类方法普遍存在计算复杂度高的问题。基于密度的异常检测方法以局部离群因子(local outlier factor, LOF)算法为代表[6]，通过计算每个数据点的邻域LOF值判断其是否为异常点，LOF值越大，说明其邻域数据密度越低，越可能是异常数据点。基于聚类的方法以DBSCAN、k-means为代表，其基本思想是将数据集根据相关程度划分为不同的簇，距离簇中心较远的数据点即为异常点，该类方法具有原理简单、容易实现的优点，但是该类方法在使用过程中需要预先设置聚类个数，在先验信息缺乏的条件下难以获得较好的检测效果[7]。基于分类的方法以支撑向量数据描述(support vector data description, SVDD)为代表，只需要带标签的正常样本作为训练集即可构建闭合曲面实现异常检测，但是检测结果依赖于模型参数的选择。目前常用的经验试错法存在主观性强、运算量大的问题。此外，由于数据集中通常会存在冗余特征，这些特征的存在不仅需要消耗大量的运算资源，同时还会降低检测性能[8]。

在上述研究的基础上，针对SVDD异常检测方法的特征提取和参数设置问题，本文将主分量分析(principal component analysis, PCA)与SVDD相结合，利用PCA对数据进行分析，自动提取对检测性能影响较大的主分量构成特征向量，然后利用SVDD构建一类分类器进行分类判决，同时针对SVDD核参数和惩罚因子的设置问题，利用粒子群算法(particle swarm optimization, PSO)进行全局寻优，以提升算法性能。

1 PSO优化SVDD分类算法

1.1 SVDD一类分类器

实际工程实践中，导致数据出现异常的原因复杂多样，异常数据表现形式千变万化，出现时机随机变化，通常无法获取足够多的异常数据样本用于模型训练。而SVDD作为一种经典的一类分类器，在构造最优分类面时只需要正常类数据样本，大大降低了数据获取难度。

(1)

其中，c和r分别为超球体的球心和半径，ξi为每个训练样本对应的松弛变量，用于降低异常值对最优分类面的影响，C为惩罚因子，影响着训练样本集对应的决策边界。

为了解决真实数据不符合球状分布的问题，SVDD通常采用高斯核函数将数据映射至高维空间中进行分析，高斯核函数的具体形式为

(2)

式中，σ为高斯核参数。为了对式(1)进行求解，可以将式(1)转化为如下的对偶形式：

(3)

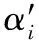
(4)

对于任意未知测试样本x*，SVDD利用最优超球体对其进行判决的决策方程为

(5)

若计算得到f(x*)≤0，表明x*处于超球体内部为正常数据，否则x*为异常数据。

1.2 PSO算法

从上述分析可知，SVDD最优超球体的形状由核参数σ和惩罚因子C共同决定，要想得到最优分类性能，需要对σ和C联合优化。粒子群(particle swarm optimization, PSO)算法由于具备算法简单，需要调整的参数较少，全局搜索和局部搜索能力均衡等优点被广泛应用于数学优化领域[9]。因此，本文将PSO引入SVDD模型，将SVDD的核参数和惩罚因子作为PSO的粒子进行优化，以提升SVDD算法性能。

(6)

(7)

其中，t为当前迭代次数，T为总迭代次数，wmax和wmin为w取值的最大和最小值。

2 基于PCA的特征提取

主分量分析(principal component analysis, PCA)是当前数据处理领域最具代表性的一种数据降维方法。其基本思想是将数据中具备相关性的指标重新进行线性组合得到数量较少且互不相关的综合性指标，这些综合性指标被称为主分量，主分量能够最大限度地反应原始数据中的有用信息。

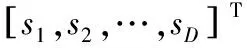
步骤1 计算观测数据的协方差矩阵R：

(8)

其中，E(·)表示求括号内变量的期望运算，U为S的均值。

步骤2 对步骤1得到的协方差矩阵进行特征值分解，得到特征向量：

(9)

其中，λ和u分别为协方差矩阵的特征值和特征向量，且λ1≥λ2≥…≥σ2=…=σ2，σ2为噪声方差。

从式(9)可以看出，对协方差矩阵进行特征值分解可以得到两部分：前K个特征值较大，对应特征向量为主分量，包含了原始数据中的绝大部分有用信息；后D-K个特征值较小，对应的特征向量为次分量，主要包含数据中的随机噪声。

步骤3 将占特征值谱总能量90%的大特征值个数作为主分量个数K，即：

(10)

步骤4 将原始数据投影到K个主分量张成的空间中实现数据降维，即：

(11)

3 算法总结

图1给出了本文所提基于PCA联合PSO-SVDD的异常检测算法流程图，可以看出算法包含训练和测试2个阶段。

图1 PCA联合PSO-SVDD的异常检测算法流程图

在训练阶段，首先利用PCA对正常数据构成的训练集进行分析，提取前K个主分量作为特征从而实现数据降维；然后利用特征向量对第1章节所提PSO-SVDD算法进行训练，并最终获得最优分类面。

在测试阶段，对于输入的测试数据，首先同样采用PCA进行分析，提取前K个主分量作为特征向量；然后利用训练阶段获得的最优分类面进行分类判决，并输出最终的判决结果。

4 试验及分析

本文通过2部分试验对所提PCA联合PSO-SVDD的异常数据检测性能进行验证。

4.1节采用4个UCI标准数据集，即Iris、Wisconsin、Biomed和Wine。其中，只有Biomed的类别数为2类，其他3个数据集的类别数都多于2类，因此将其人为的划分为2个类别。对于Iris数据集，规定类别标号为Iris-setosa的数据为正常样本，其余为异常数据；对于Wisconsin数据集，规定类别标号为malignant的数据为正常样本，其余为异常数据；对于Wine数据集，规定类别标号为1的数据为正常样本，其余为异常数据。试验中，分别采用本文所提方法、PCA联合SVDD方法和PSO-SVDD方法(不进行特征提取)3种方法开展试验，在相同条件下对试验结果进行对比。

4.2节采用某市电网用户连续用电负荷数据集，采样频率为1次/H，数据集中包含93个电力用户，其中30户为正常用户，3户为异常用户，异常用户比例为3.2%。试验中，采用所提方法对该实测数据集进行异常检测，验证所提方法在实际场景下的性能。

4.1 UCI标准数据集实验结果

试验中，首先从每类数据集中随机选取80%的正常数据作为训练样本集。根据图1所示流程，利用PCA对其进行特征提取和降维，每类数据集得到的主分量个数K如表1所示。其中，#POS和#NEG分别为每类数据集中的正常数据个数以及异常数据个数。

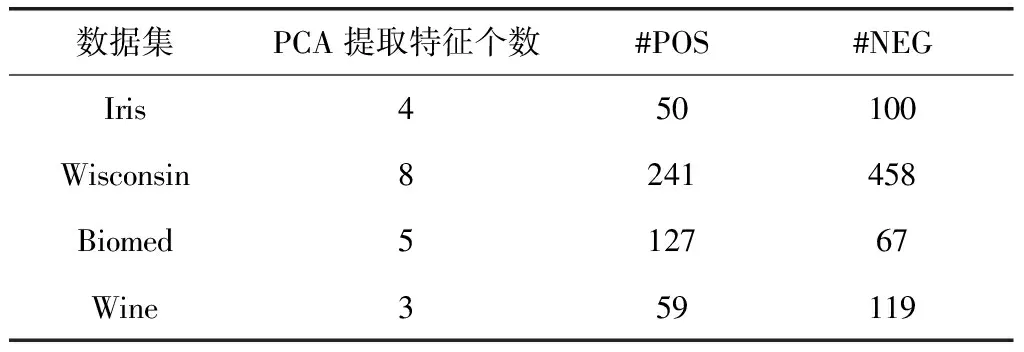
表1 UCI试验数据集

初始化PSO算法时，设置初始种群数量为10，算法最大迭代次数为100次，粒子位置信息设置为2，初始的粒子速度设置为0.1。利用所提方法(PCA+PSO-SVDD)，与PCA-SVDD方法和PSO-SVDD方法(不进行特征提取)对表1中的数据进行试验得到的异常检测准确率结果如表2所示。

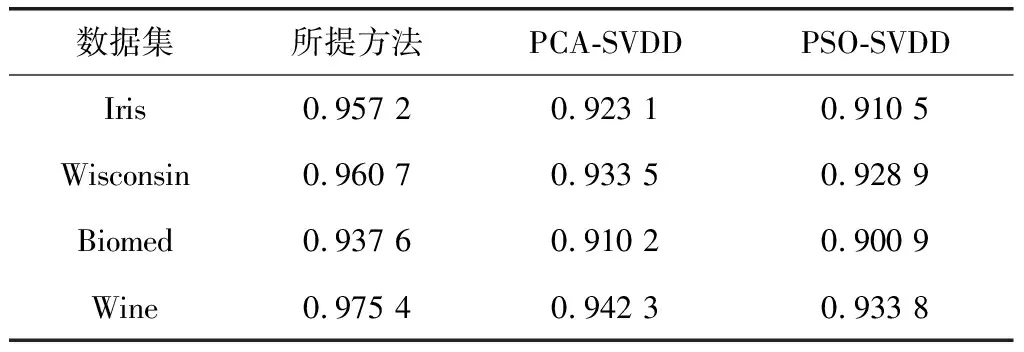
表2 三种方法的异常检测结果

从表2可以看出，所提方法在4种UCI数据集上得到的异常检测性能均优于另外2种对比方法。其中，所提方法相对于PCA-SVDD的异常检测准确率更高，说明经PSO优化后，SVDD的性能出现了明显提升；而所提方法相对于PSO-SVDD的异常检测正确率更高，说明了特征提取的必要性。上述结论有力地支撑了本文所述内容。

4.2 所提方法在电力用户异常数据检测中的应用

试验中，随机从90个正常用户中选取80个用户数据作为训练样本集，利用PCA算法对其进行特征提取和降维，最终得到的主分量个数K=2，将其构建特征向量并对PSO-SVDD分类器进行训练得到最优分类面，然后根据图1所示流程算法进入测试阶段。首先对10个正常用户和3个异常用户组成的测试样本集进行PCA分解；然后利用训练阶段获得的SVDD最优分类面对其进行分类判决，从而实现异常检测。从图2给出的最终判决结果可以看出，测试数据中的3组异常样本全部落在最优分类面之外，测试样本中的15组正常样本全部落在最优分类面以内，表明测试数据集中的所有样本均被正确判决，验证了所提方法的有效性。

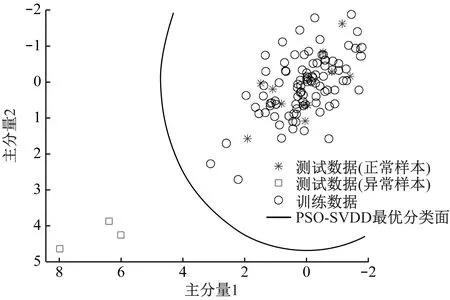
图2 异常检测结果

5 总结

作为一种经典的异常检测算法，SVDD的性能受核参数和惩罚因子影响较大，并且在面对高维复杂数据时存在运算量大、实时性差的问题。本文将PCA与SVDD相结合，提出一种改进的异常数据检测方法。首先利用PCA对高维数据进行特征提取和降维，从而提升SVDD的运算效率；然后针对SVDD模型参数选择问题，将PSO算法引入对其优化，自动确定最优模型参数，基于UCI公共数据集和实际电力用户异常数据检测问题开展试验，结果表明所提方法能够有效实现异常数据检测，并且相对于对比方法具有更高的异常检测性能，具有较好的应用前景。