基于SVC的考试时间安排的实现

殷玉霞， 张彬， 帅小应

(泰州学院，1.图书馆，2.信息工程学院，江苏，泰州 225300)

0 引言

考试安排是学校考试均要面对的问题，随着高校在校生人数以及专业数量的增加，尤其是选修课程的增多，这些都带给考试安排工作不小的压力。同一学生选修的多门课程不能安排在同一时间段参加考试。考试安排工作是一种典型的调度问题，在有限的时间区域约束条件下寻找最优解使得考试安排的周期最短。

针对考试安排问题，张磊等[1]建立学生选课关系图，运用关系着色图对时间表问题进行了研究，开发了业余大学的考试安排系统。针对学校希望缩短考试周期而学生渴望增大考试间隔的矛盾，运用分组遗传算法优化大学考试时间表[2]。针对课程排考问题，李睿等[3]改进了FFD算法并将其应用在解决此类问题中。学生选修课程间的关系可用无向图来表示，课程当作图中的顶点，用边连接有学生同时选修的两门课程，相连接的课程不能安排在同一时考试。利用序列点着色(SVC，sequential vertex coloring)能很好解决考试安排问题。序列点着色是按照节点的度对节点进行降序排列，依次对节点进行着色，第1个节点着上颜色1；然后向后顺序查找没有着色的结点，用最小可用的颜色着色，直到所有节点均着上色[4]。马国强等[5]利用微信小程序设计与开发了能发考试信息、安排考试时间的考试安排系统。针对高校考试安排中的资源、任务与时间分配合理要求，张培培等[6]利用贪心法设计了考试安排系统。本文利用贪心法与序列点着色方法选择节点度最大的课程优先安排考试，直到所有的课程均安排为止，算法在确定考试安排周期最短的情况下提高了安排的灵活性。

1 问题建模

考试安排实际是时间表问题，其与教师、教室、时间、课程等诸多因素有关，是一个多约束条件的目标优化问题。同一个学生选修的若干门课程不能安排在同一场次考试。课程间的关系可用无向图来表示，顶点表示课程，若两门课被同一个学生选修则这门课程间用边连接。

表1为某班部分学生的选课表，则此部同学的选课关系可用图1来表示。张山选修了“算法设计”与“神经网络”，这两门课程分别用点A与点B表示并用边(A，B)连接。

表1 学生选课表

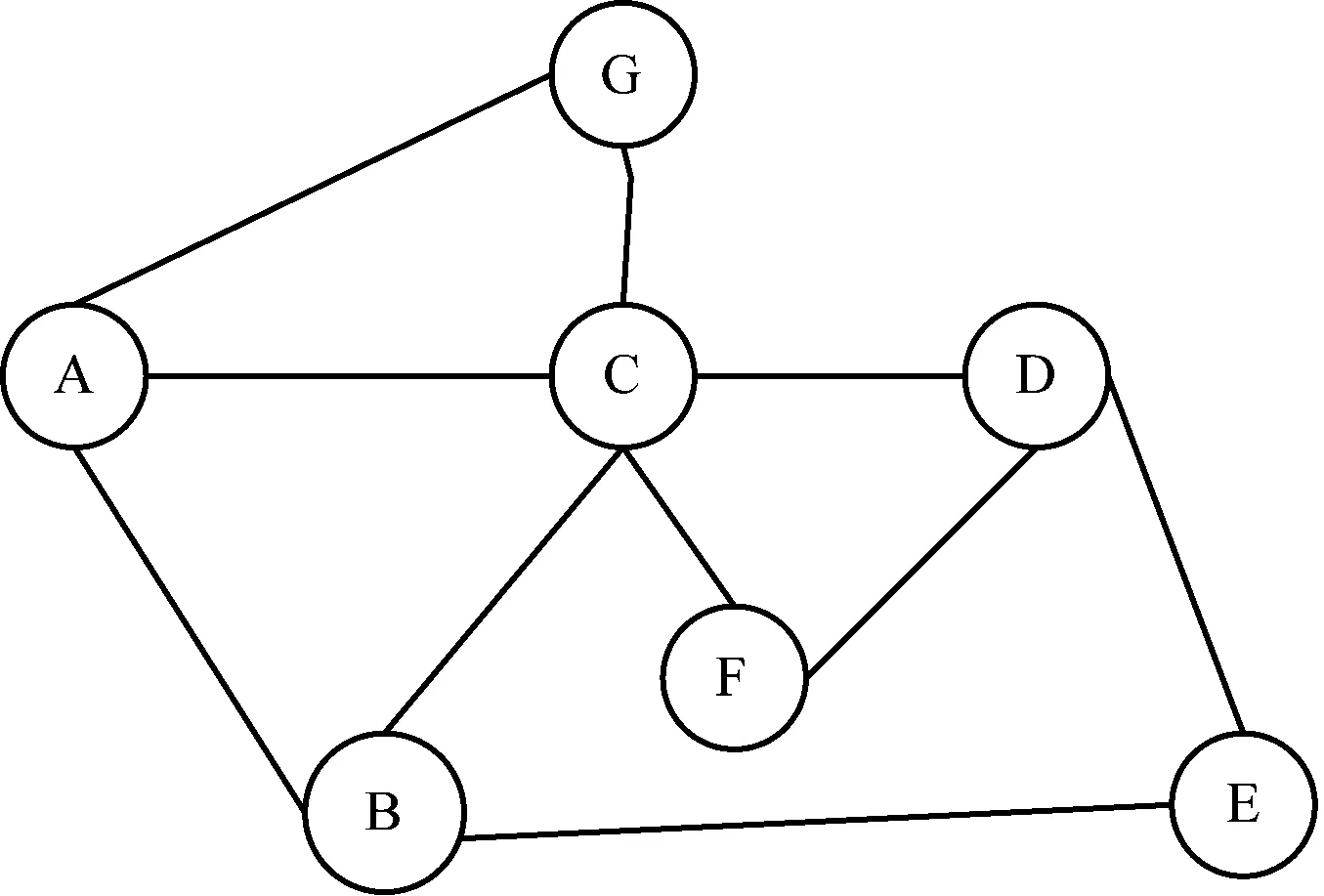
图1 课程关系图

若两个顶点间有边则表示不能安排在同一场次考试，考试安排问题能够用图的着色方法解决。如图1，顶点A与B间有边(A，B)，则分别上不同的两种颜色，A与B不能安排在同场考试。用最少色数使得所有的顶点着上色。用dij表示课程i与课程j冲突，如式(1)，全部选修课程的冲突矩阵如图2。没有冲突的课程可以安排在同一场次考试。

图2 冲突矩阵

(1)

课程i安排在第j场考试则Sij设置为1，如式(2)。

(2)

考试安排解决在一定约束条件下周期最短的优化问题；设K为考试场数，同一时间段内的考试为1场；N为课程总数，考试安排目标如下：

(3)

约束条件：

(4)

(5)

约束条件(4)表示每门课程均要安排考试，约束条件(5)表示冲突的任意两门课程不能安排在同一场次考试。

2 算法

2.1 SVC算法

SVC算法对节点进行排列，然后依次对节点进行着色，第1个节点着颜色1；向后顺序查找没有着色的结点，用最小可用的颜色着色，直到所有节点均着上色。算法如下：

算法1

输入：顶点数N

输出：颜色数c

Order nodes by specified criterion as 1,2,…,N

Colorc=1;

i=1;

While(i<=N)

Forj=1 tocdo

If vertex can color withjthen color; break;

EndFor

If(j>c)then colorc++;

i++;

EndWhile

2.2 最小化考试周期

安排考试时优先安排与其他课程冲突大的课程即图中顶点度数大的课程，再安排冲突小的课程。首先按照节点的度对课程进行降序排列；然后依次对课程进行考试时间安排，第1门课程安排第1场次；再向后顺序查找没有安排的课程，用最小可用的场次安排考试，直到所有课程都安排了为止，具体如算法2。

算法2

输入：课程数N

输出：考试安排

按度对课程进行降序排列

初始化，场次k=1;课程i=1

While(i<=N)

j=1;Sij=0;

While 课程i不能安排在j场考试

j++;

EndWhile

Ifj>kthenk=j;

Sij=1;

i++;

EndWhile

2.3 场次调整

经过算法2每门课程均会合理分配考试的时间，但考试受到多种因素的影响，某门课程的安排可能会发生变动。为了在不增加考试周期的情况下灵活利用场次的安排，可人工指定若干门考试课程的考试场次，也可以利用算法3在算法2结果的基础上为一门课程提供若干个可能的考试时间选择。

算法3

输入：考试安排表

输出：新考试安排表

对课程进行排序

Fori=1 toN

Forj=1 tok

如果课程i也可以安排在j场次进行考试，则Sij=1

EndFor

EndFor

3 仿真实验

运用C语言在Win 10系统中设计仿真程序，分别对图1与图3的课程进行考试安排。首先运行算法2，安排结果如表2；再运行算法3，安排结果如表3。

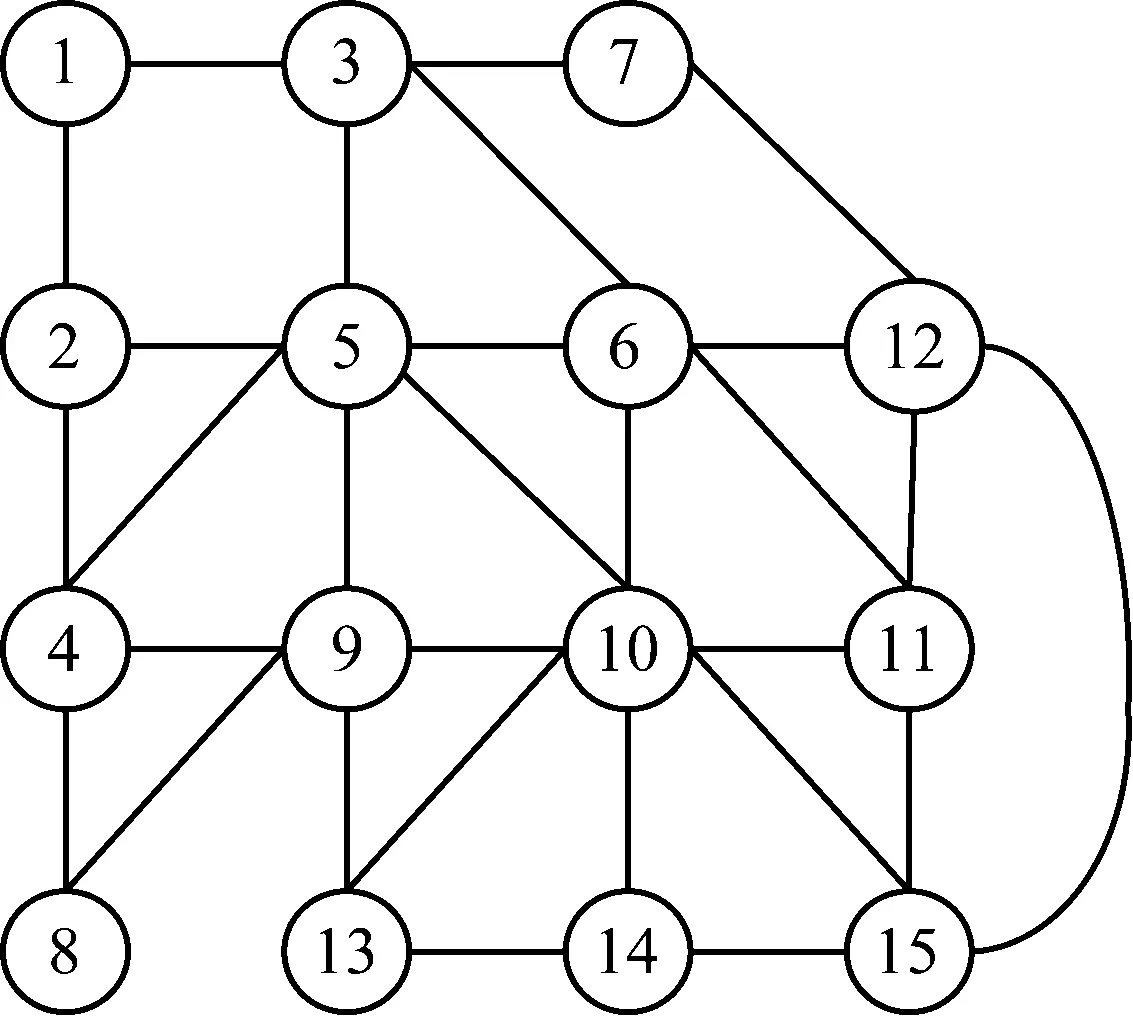
图3 15门课程的选课关系图

表2 安排结果

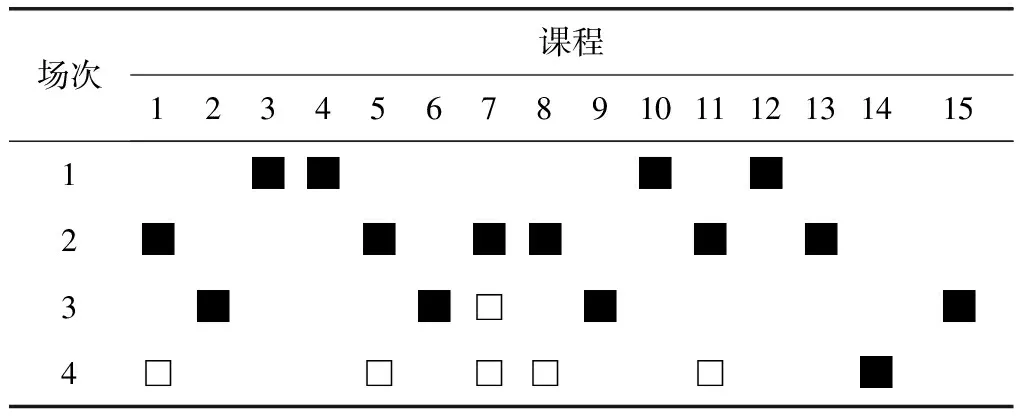
表3 安排结果

4 总结

考试时间安排问题是高校教务期末工作的重点与难点问题，随着学生人数与选修课程数的增多，考试安排问题也越来越复杂。把考试课程间的关系用图结构来表示，利用序列点着色算法与贪心法对考试时间进行安排，得到周期最短的无冲突的考试安排。仿真结果表明本算法能有效地解决考试时间安排问题。考试安排受到多种条件的约束，本算法没有考虑到同一个学生考试间隔安排问题。今后将进一步探讨实际运用中各种约束条件下的安排优化问题，如考试周期最短的前提下同一个学生选修课程考试间隔问题等。