基于SPC的卷烟车间产品质量全周期监控方法研究

周江建， 袁媛， 王季强

(1.江苏中烟工业有限责任公司，江苏，南京 210009；2.上海威士顿信息技术股份有限公司，上海 200052)

0 引言

近年来，人们对于卷烟的需求越来越大，卷烟市场逐渐形成了一个庞大的发展体系。为满足市场需求，传统方法根据数据挖掘算法、神经网络算法以及自动化智能技术实现了卷烟车间产品质量的监控，但在传统方法应用实际调查中发现这三种传统方法存在不同程度的不足。

因此，本文研究基于SPC的卷烟车间产品质量全周期监控方法。

1 基于SPC的卷烟车间产品质量全周期监控方法

1.1 设置全周期监控SPC模式

SPC为产品质量统计过程控制概念，在产品的整个生产周期中，通过对各个阶段的样本数据进行分析，得到产品在不同生产环节中的质量波动情况[1]。由于产品质量存在波动特征，因此可借助SPC分析产品的生产过程，选择质量分布图、过程能力指数以及过程控制图作为设置全周期监控SPC模式的基本工具，利用质量分布图监控产品质量状况，并找出其中存在质量波动的环节[2]。该图像根据收集到的产品质量特征值分组，组距值可通过下式获得：

(1)

式中，di表示第i组的组距，qmax、qmin分别表示质量的最大值和最小值，n表示分组数量。根据上述计算结果，以组号和频数为横纵坐标，按照从小到大的顺序绘制质量分布图，实现对某一生产环节的质量监控。工序能力指数是稳定状态下生产产品时的实际产能，当该指数越大时，越能说明产品质量特征值越集中，生产的卷烟产品更加满足生产质量要求。假设工序能力指数为Cp，则量化该指数的计算步骤为

(2)

式中，ΔC1、ΔC2分别表示上公差限和下公差限，σ表示质量特征值的标准差。当产品特征值公差中心与分布中心重叠时，则通过上述计算过程获得工序能力指数的量化值[3-4]，但公式中的标准差σ并不是已知的，因此根据式(3)得到不同生产环节中工序能力指数的整体标准差：

(3)

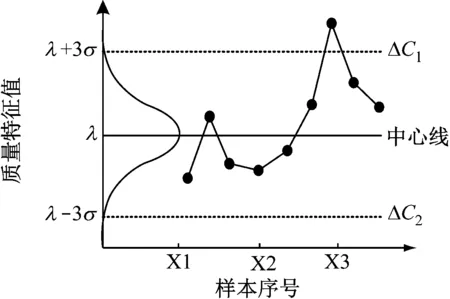
图1 控制图简图

综合上述三组工具，设置全周期监控SPC模式，获得更加详细的卷烟车间产品质量特征。

1.2 基于k-means算法的SPC控制图特征提取

k-means算法基于样本间相似性度量同属性的特征值，因此利用k-means算法提取SPC控制图特征。假设一共存在n个数据，利用该算法从中选择s个数据作为初始聚类中心，其他数据则根据设置的初始聚类中心距离被分配到不同的类别中；然后计算新聚类的聚类中心，得到所有数据的平均结果；不断重复上述计算过程，直至标准测度函数收敛[6]。设按照上述步骤得到的初始聚类中心为Xj(I)，每个数据样本到每一个聚类中心的距离可通过D(bi,Xj(I))表示。设置允许条件为D(bi,Xj(I))=min{D(bi,Xj(I))}，其中bi∈Xj，表示其中的第j个类别[7-8]。根据新的类别划分结果，计算s个新的聚类中心：

(4)

式中,nj表示类别Xj中的数据数量,b表示被划分到Xj中的数据样本。Xj(I+1)≠Xj时，此时存在I+1=I，说明误差平方和计算结果无效，则重新计算每个数据样本到每一个聚类中心的距离；当Xj(I+1)=Xj时，则算法完成对数据特征值的聚类。根据质量分布图、过程能力指数以及过程控制图设置的全周期监控SPC模式由两个模块组成，可以对各个环节中的生产过程进行监控。而应用k-means算法可以减少SPC模式的维度，然后各个模块用训练好的多分类，识别SPC模式的类型[9],该过程中需要利用k-means算法从SPC模式中提取距离特征，将其作为全周期监控的分类模块输入参数[10]。因此,利用该算法将控制图模式的数据集聚为k类，然后计算每个SPC模式到各个聚类中心的欧氏距离，得到不同的距离特征结果,最后将该结果以集合的形式进行整理，作为分类器的输入来源。欧式距离的计算公式为

(5)

式中,D(A,B)表示随机两个点A和B之间的欧式距离,g表示迭代次数,ai、bi表示其中第i组节点之间的差异量[11]。通过上述计算过程，应用k-means算法提取SPC控制图特征。

1.3 质量监控算法全周期监控产品质量

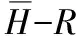
(6)

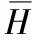
f(6)-(1-f(6))=2G(6)-1

(7)

式中,h表示各个特征值,t表示监控周期[14]。根据上述计算结果，将λ-6σ和λ+6σ分别设定为监控下限和上限，计算样本平均值：

(8)

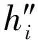
(9)

式中,L1、L2分别表示经过SPC模型的混合处理后，得到的最新的上公差界限和下公差界限。根据式(5)设定监控组别，得到每一生产环节中的工序能力指数，至此通过质量监控算法，实现基于SPC的卷烟车间产品质量全周期监控[15]。

2 仿真实验

2.1 实验准备

选择4个工作任务相同的卷烟车间作为实验测试环境，测量不同监控方法应用下，产品质量的全周期监控效果，同时比较4组车间的生产成本。实验开始前要保证所有生产机床工作稳定、材料充足。影响卷烟产品生产质量的主要因素包括材料的进给量和切割速度，因此将该条件作为实验测试变量，通过调整材料的进给量和切割速度设定监测环境。表1数据为进给量参数和切割速度参数对应的卷烟产品粗糙度。

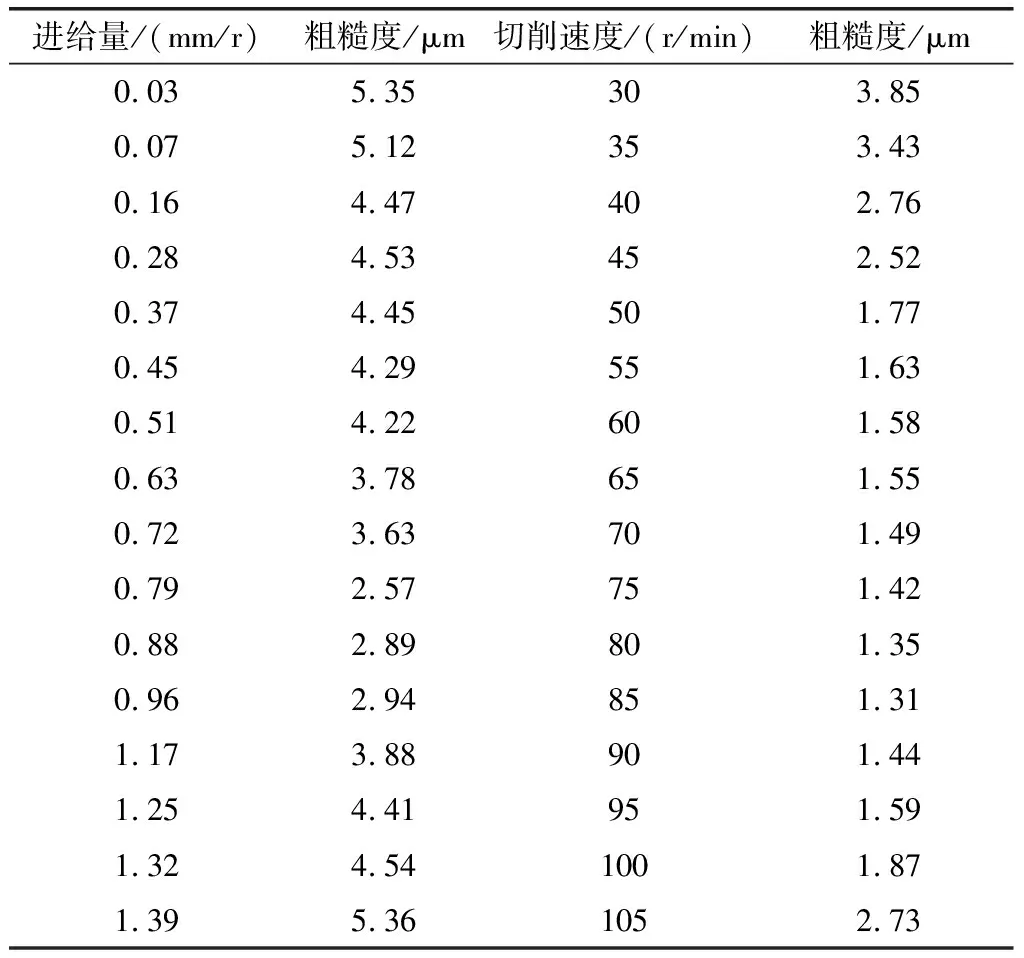
表1 材料进给量和切割速度与对应的产品粗糙度

根据表1中的数据可知，并不是进给量越大、切削速度越大，产品粗糙度就会随之升高或降低的,因此制作进给量与粗糙度、切削速度与粗糙度的散点图，如图2所示。

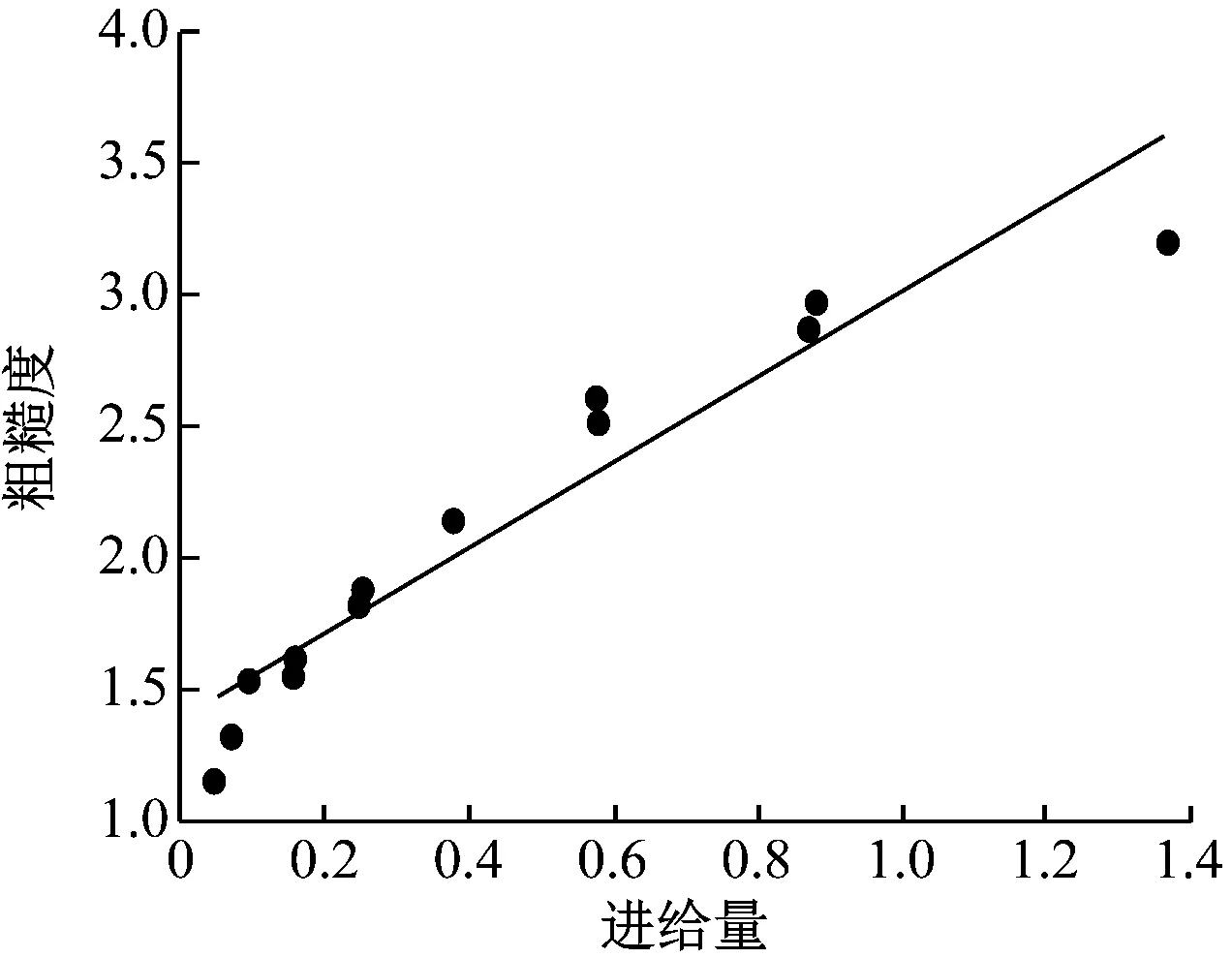
(a)进给量与粗糙度

根据图2的散点图可知，当进给量和切削速度偏小或偏大时，产品粗糙度都会处于不同的数值，只有两个参数都适中，才能将产品粗糙度控制在最小。因此根据上述准备，建立存在操作问题的生成程序，满足实验测试环境要求，开始实验。

2.2 全周期监控效果分析

将此次研究的方法作为实验组，将3种传统监控方法分别作为对照A组、对照B组和对照C组，在上述建立的测试环境下，对卷烟车间产品质量进行全周期监控，得到的结果如图3所示。

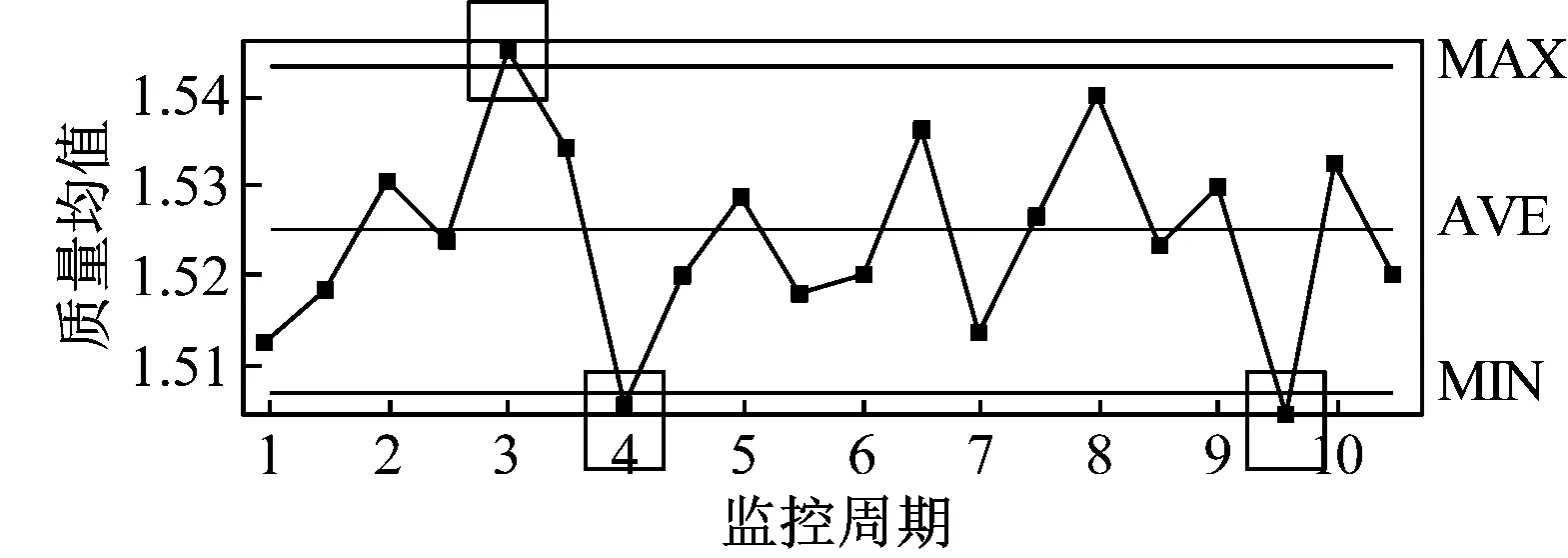
(a)实验组

根据图3中的测试结果可知，实验组不仅计算了每一周期内的质量均值，还明确了超出允许极限的监控数据，同时根据监控结果给出了极差值，可以通过该值快速找到问题所在，解决存在问题的生成环节和程序;对照A组给出了每一周期、每一特殊环节的质量监控结果；对照B组仅在每一周期结束时给出质量监控结果，2种方法无法确定质量参数是否低于质量限值，同时针对存在问题的环节，也无法确定极差;对照C组只能在完成所有生产环节后，才能给出产品质量监控结果，无法在任意一个子周期内发现产品质量问题。可见此次提出的监控方法，在质量问题初期就能确定存在问题的环节，同时给出详细的极差数据。

2.3 车间生产成本分析

根据4个不同的监控方法，对卷烟车间产品质量进行全周期监控，设置一个生产总量和产品质量等级，利用4个车间分别生产一定目标数量的卷烟产品，利用下列方程组计算生产过程中涉及到的各项费用，以此求得总生产成本。该计算过程如下。

已知生产成本由直接费用和制造费用构成，其中直接费用包括直接材料费、直接工资和福利费用以及其他直接支出。因此根据上述费用明细科目，计算直接费用值：

K1=Q1+Q2+Q3

(10)

式中，K1表示直接费用，Q1、Q2以及Q3分别对应各自的费用二级科目。假定制造费用为K2，则车间生产成本的计算公式为

C=K1+K2

(11)

根据上述计算公式，计算同样的生产质量要求下4组监控方法应用下的车间生产成本，结果如表2所示。

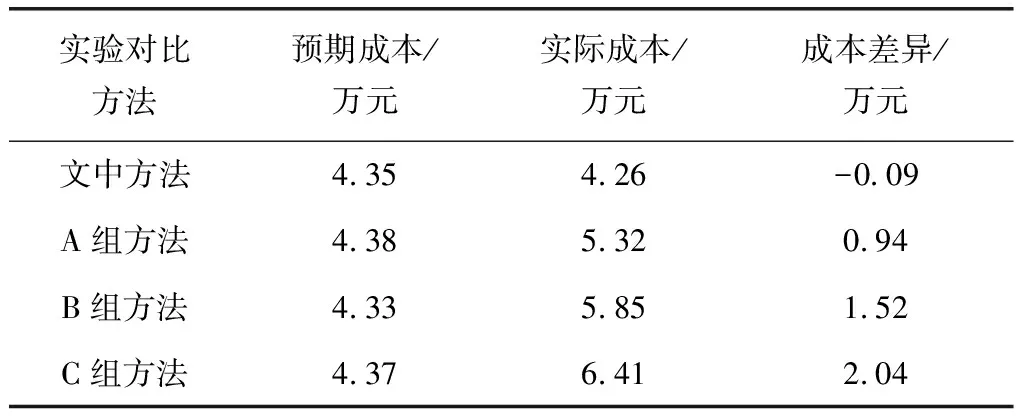
表2 车间生产成本统计

根据表2中的计算结果可知，4种方法的实际生产成本统计结果中，只有文中方法的成本低于预期，而其他3组在传统监控方法应用下，其实际成本均超出预期成本0.94万元、1.52万元以及2.04万元。由于设置的生产项目一致，因此忽略预期成本之间的微弱差异，纵向对比4种监控方法应用下车间产品的生产成本，文中方法应用下的车间生产成本，比3组传统方法应用下的车间生产成本，分别低了1.06万元、1.59万元以及2.15万元。

3 总结

此次研究在传统监控方法的基础上，利用SPC控制图加强了产品质量的监控效果。但此次研究过程中涉及大量的数据计算，增加了方法的实现难度，因此在今后的研究中，需要设计一套检测算法，对各项计算公式进行实时验证，保证整个监控过程的流畅性和数据的准确性，为卷烟制造提供更加可靠的技术支持。