基于接触式轮廓仪的工件参数校正模型建立与应用

王阿利

(咸阳职业技术学院, 基础教学部，陕西，咸阳 712000)

0 引言

随着测量技术的飞速发展，轮廓仪成为检测工件表面粗糙程度的重要工具[1-2]，但由于工程工件使用频次增多，工件的表面受到了一定程度的磨损，这些磨损很大程度上影响着工件的工作性能。为保证工程工件的工作精度，需要通过技术手段对工件的表面轮廓进行测量、修正。目前，根据测量方式，轮廓仪可分为接触式测量和非接触式测量两类[3]。由于非接触式轮廓仪对工件轮廓表面测量要采用光学系统进行扫描和图像图形处理等技术，测量误差受工件表面粗糙度影响较大，因此在实际工程中很少采用。接触式测量通常采用接触式轮廓仪进行，接触式轮廓仪利用半径为微米量级的探针从被测物体表面垂直划过，再通过传感器接收被测物体表面的轮廓信息采样数据，并将其转化为电信号[4-5]。被测对象表面粗糙不平，或者轮廓仪中探针缺失、扫描不准确等现象的存在，会给工件轮廓参数的准确标注带来一定影响。因此，对于工件轮廓参数的校正研究也显得尤为重要，在现代的研究理论中，对于利用接触式轮廓仪进行工件轮廓曲线拟合也出现了许多研究方法。朱洪涛等[6]基于工件轮廓数据点，并对其进行平滑处理后，利用最小二乘拟合方法对工件轮廓曲线进行拟合，取得了满足精度要求的轮廓曲线。由于最小二乘拟合是线性估计，对于工件表面轮廓不规则曲线的使用有一定局限性，并且在工件轮廓曲线拟合过程中，每个回归数据点不可能都进行回归计算。因此，本文以此为研究背景，以两种工件轮廓测量数据为基础进行工件轮廓线参数校正、工件轮廓倾斜角度计算、模型校正等研究。

1 工件轮廓模型概述

在使用轮廓仪进行工件表面轮廓测量时，理想状态下的测量曲线应该是准确的光滑曲线，由于测量过程中自然因素和人为因素的影响，检测到的轮廓曲线可能呈现出粗糙不平的情况，给工件形状的准确标注带来影响。为进一步减弱上述问题对轮廓仪带来的影响，提高工件形状标注的准确性，本文通过对两种工件轮廓的测量数据进行分析处理，建立工件轮廓曲线参数校正模型，实现对具有倾斜角度测量值的修正。

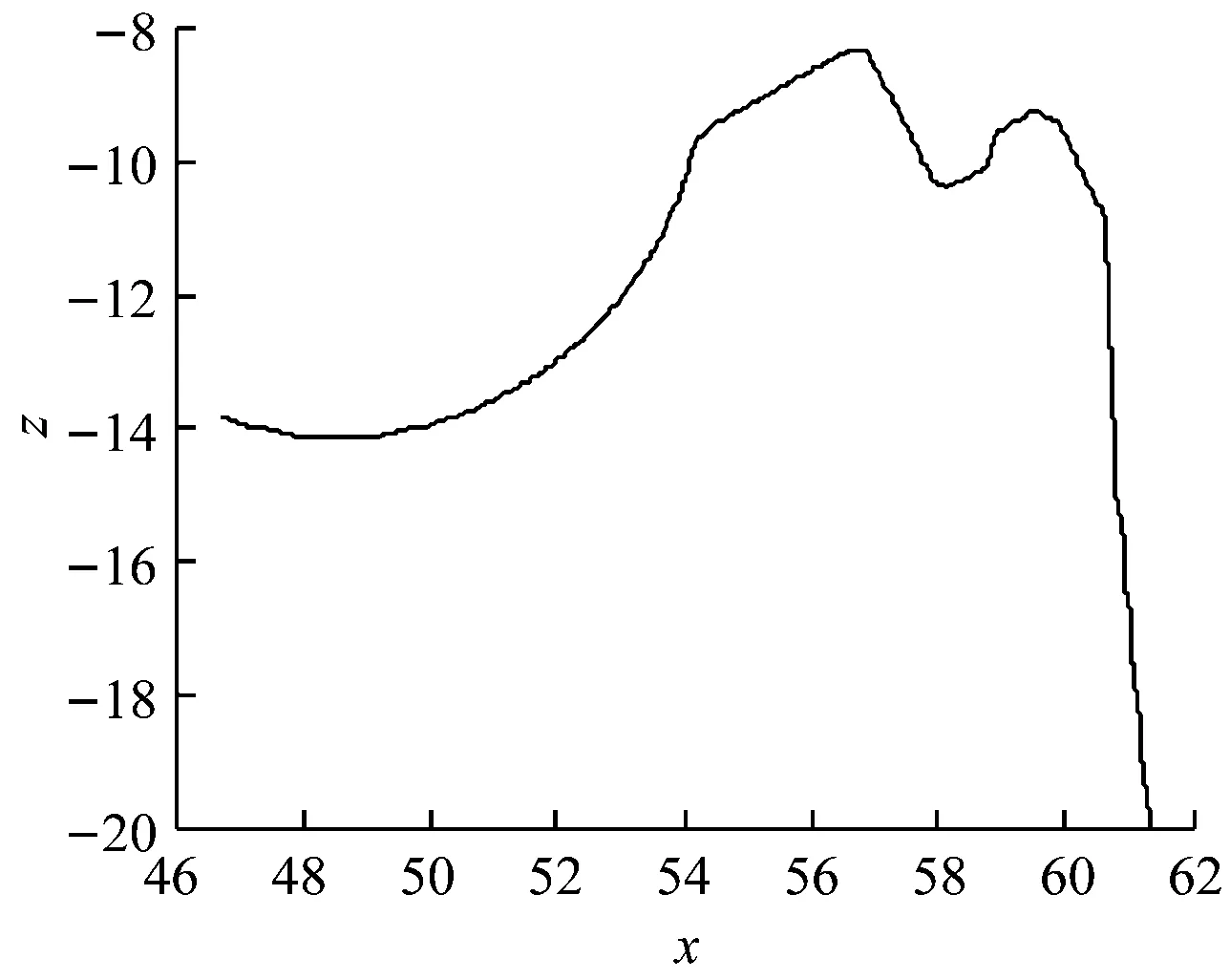
图1为某工件轮廓图，由于该工件表面轮廓较为复杂，是一个典型的复合图形，采用一条曲线对所有的轮廓点进行拟合是很难完成的，不易于求出其轮廓线的各项参数值。因此，考虑按照其实际模型特点，将工件实际拆分为8个区段进行数学拟合求解，在每个区段采用图形拐点作为其分段点，运用拟合的方程计算出圆心及半径，进而求出工件1 的各个参数值。

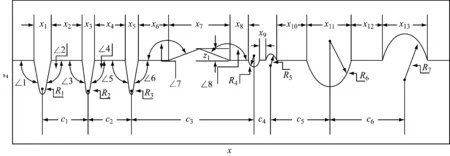
图1 工件1在水平状态下的测量轮廓线

2 工件轮廓参数修正模型的建立

2.1 工件轮廓函数拟合与参数求解

对工件1中的模型数据进行分析，利用MATLAB对每一区段的数据进行分析整合。为了更精确地拟合出圆弧的近似模型，在第一区段凹型曲线的基础上进行二次截取，得到如图2所示的凹形曲线圆弧(x轴为直线运动方向，z轴为位移测量)，使截取到的部分更接近圆的14/45弧形，其中弧长公式为d=θ*r(θ为弧长夹角)。再利用分段拟合方程进行拟合，可以得到如图3所示的拟合图形。其次，在图形曲线上取任意两点，用两点式算出其斜率k1和圆弧半径R1。第一区段的拟合方程如式(1)～式(4)所示。

图2 第一段凹型曲线圆弧

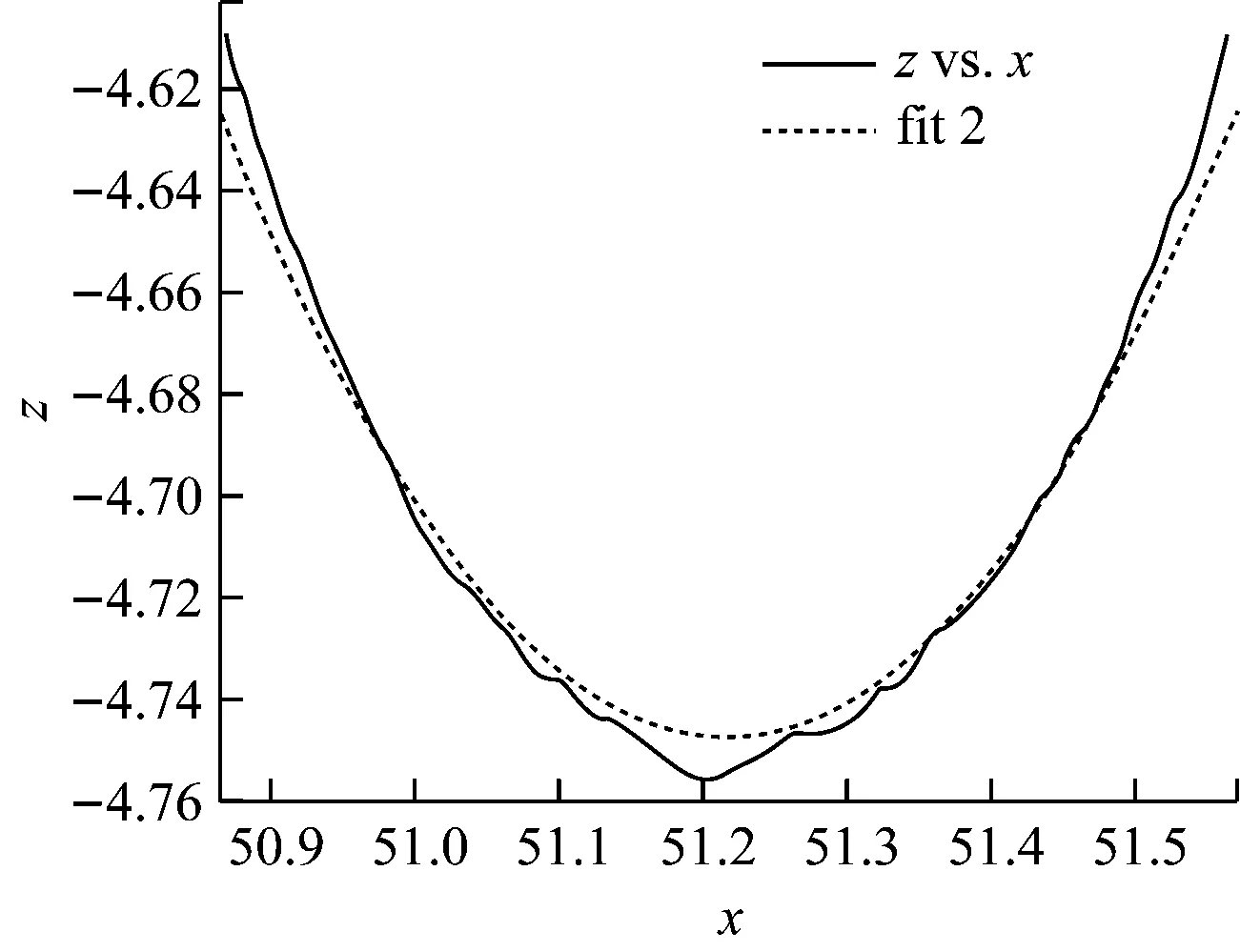
图3 第一段拟合后曲线

拟合方程：

x2+z2-102.4x+15.57z+36.51=0

(1)

斜率公式：

(2)

半径公式：

(3)

弧长公式：

d1=arctanθ1×R1

(4)

根据上式则可以计算出图1中工件参数∠1和∠2夹角的参数值为

tanθ=-2.4

(5)

∠1=112°，∠2=112°

同理可得，第二区段及第三区段的拟合图形与参数如图4～图7所示。

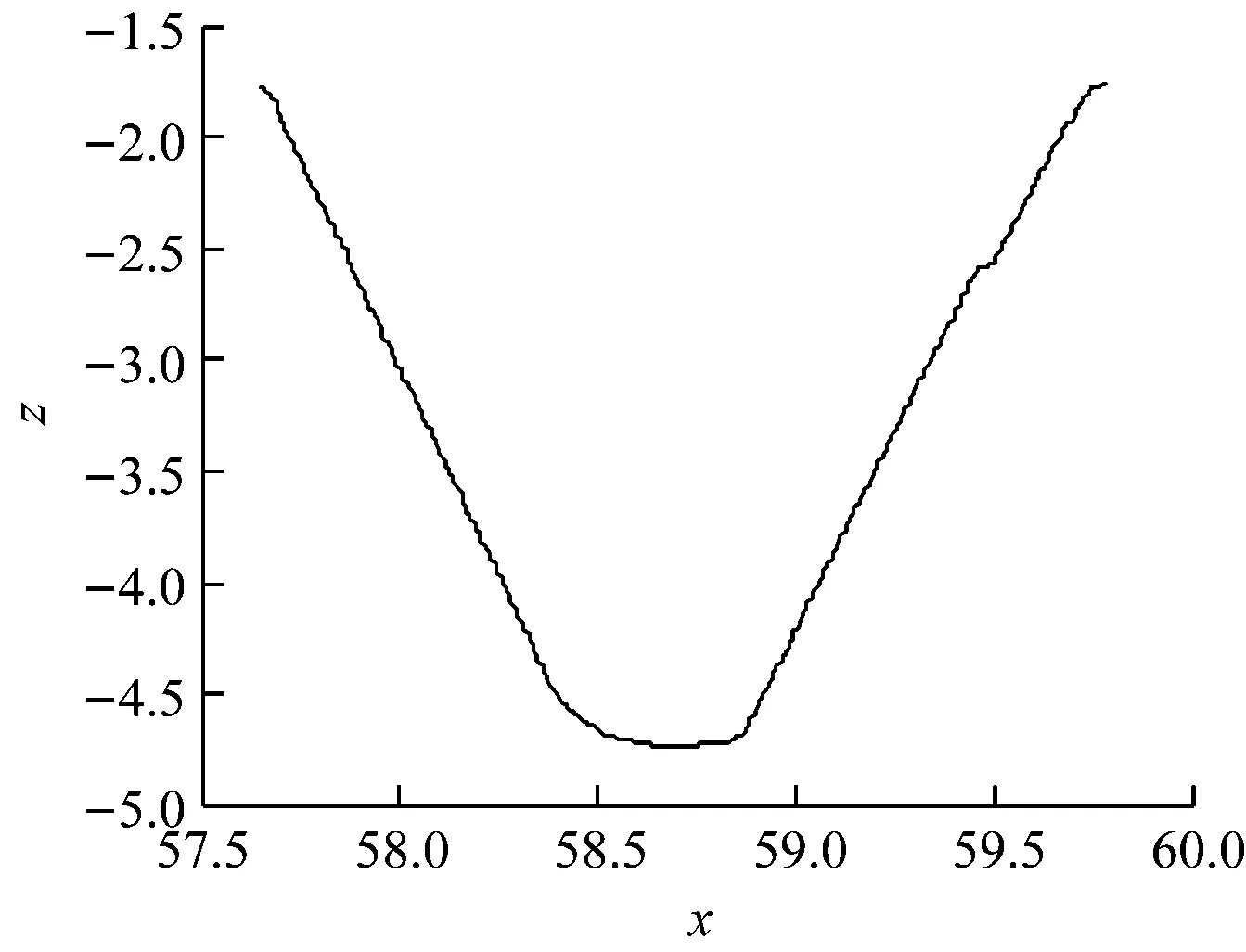
图4 第二段凹型曲线

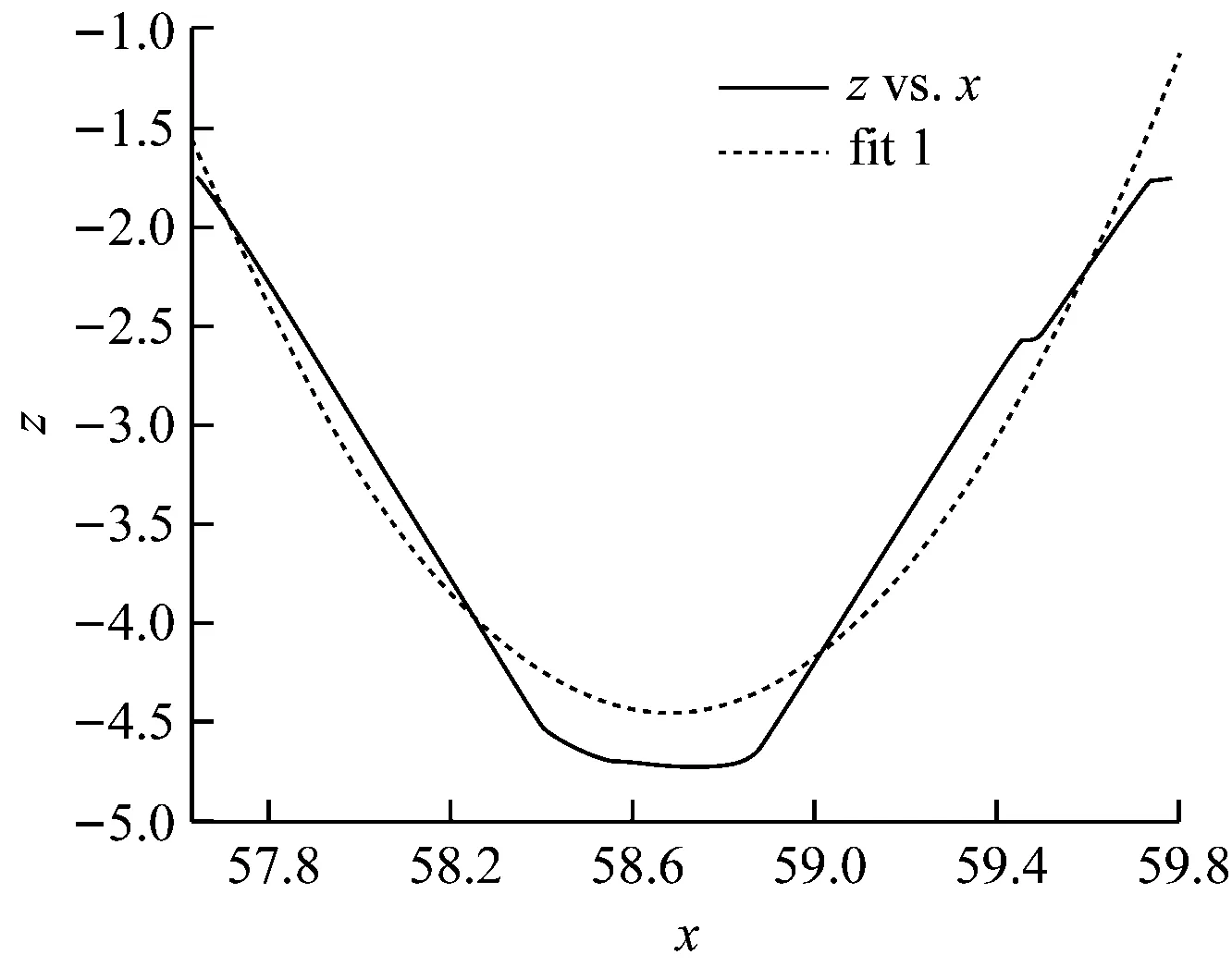
图5 第二段拟合后曲线

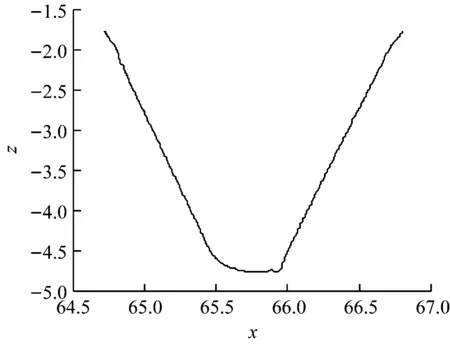
图6 第三段凹形曲线

图7 第三段拟合后曲线

第二区段的拟合方程如式(6)～式(8)所示。

拟合方程：

x2+z2-117.2x+20.81z+71.52=0

(6)

半径公式：

(7)

弧长公式：

d2=arctanθ2×R2

(8)

根据上式则可以计算出图1中工件参数∠3和∠4夹角的参数值为

tanθ=-3.48

(9)

∠3=106°，∠4=-107°

拟合方程：

x2+z2+0.116 4x-0.472 5z-4.458=0

(10)

半径公式：

(11)

弧长公式：

d3=arctanθ3×R3

(12)

根据式(10)～式(12)则可以计算出图1中的∠5和∠6夹角的参数值为

tanθ=-5.14

(13)

∠5=101°，∠6=102°

由于第四区段为规则图形(如图8)，因此根据工件轮廓数据找到第四区段对应的极值点，利用极值点可以进一步得到该区段曲线的垂直高度z值。其次，利用特殊点坐标，根据直线点线原理可以求出左、右边线段的方程如式(14)、式(15)：

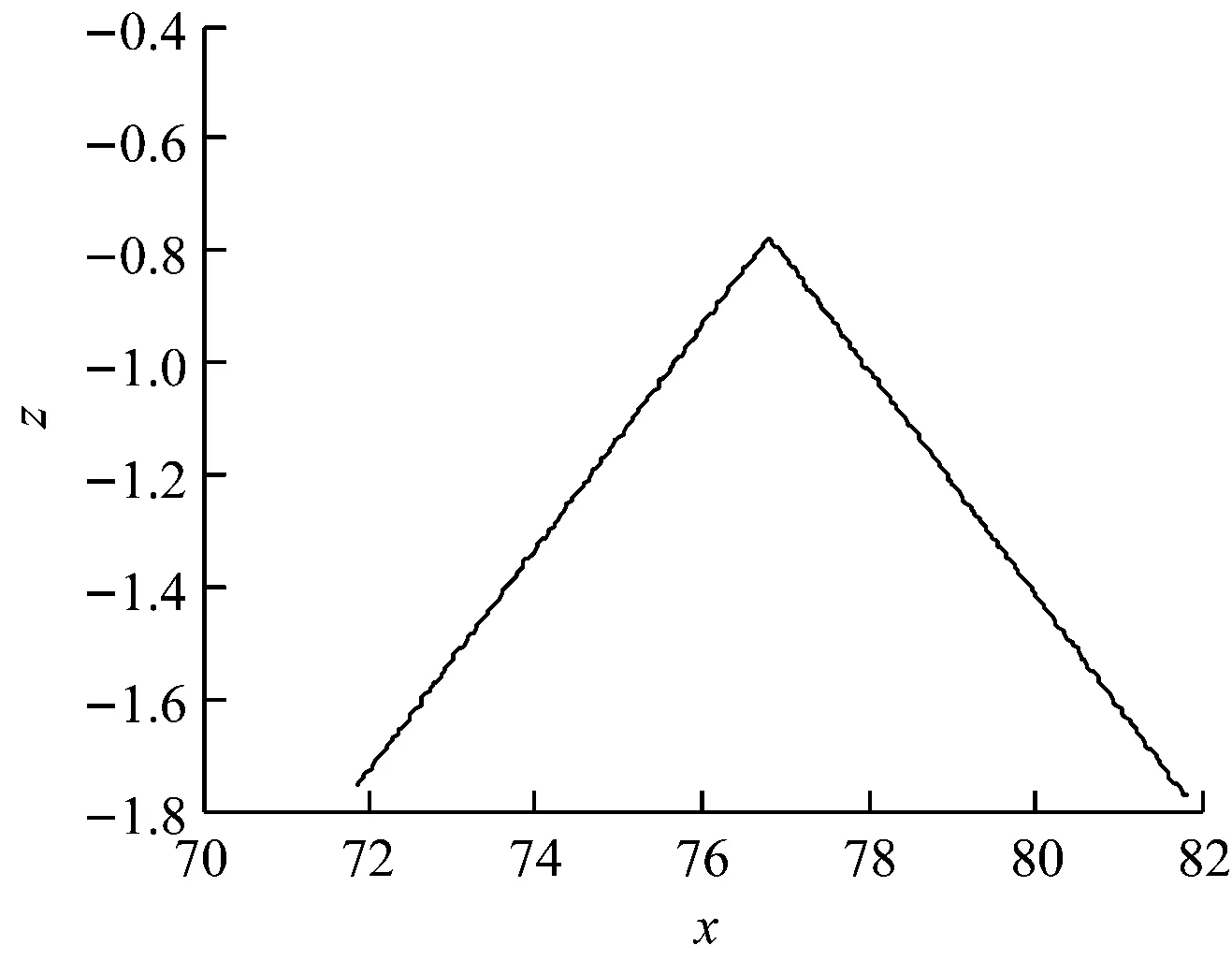
图8 第四段凹形曲线

z1=0.19x+15.39

(14)

zr=-0.2x+14.59

(15)

根据上式，则可以得到图8中曲线顶点的垂直距离为

z=0.979 368

由于第五区段近似拟合程度不高，因此将第五区段近似看成半圆图形(如图9)，应用工程设计软件截取出第五区段所在的数据区间，以数据区间上的纵坐标作为圆弧上最低点的纵坐标，再根据区间的端点值求出该段圆弧的近似拟合方程，进而可以求得该段的各个参数。

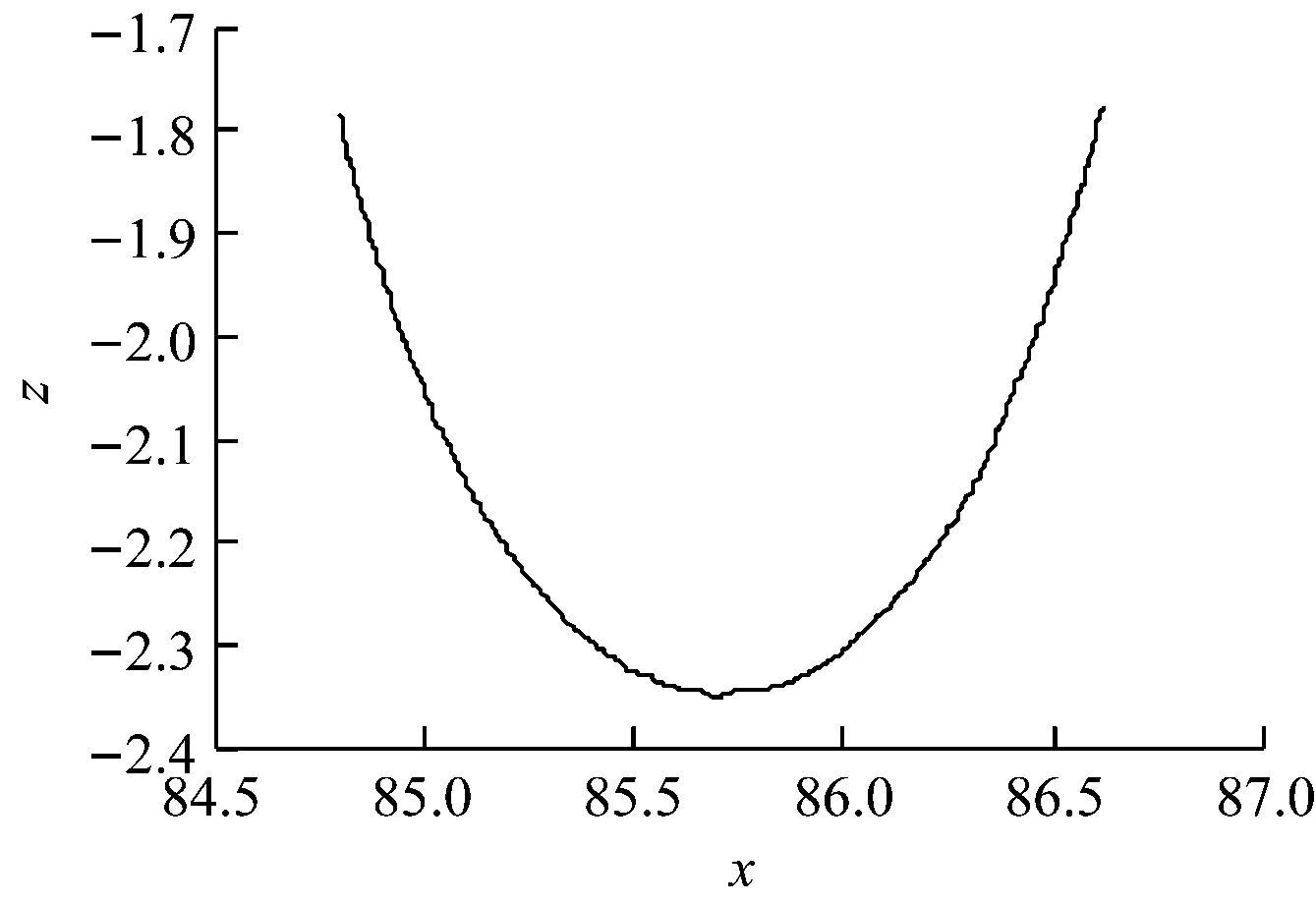
图9 第五段凹形曲线

由圆心方程得：

x2+z2-171.382 16x-3.262 06z+7 344.822 04=0

(16)

半径公式：

(17)

弧长公式：

d5=arctanθ5×R5

(18)

由于第六区段工件轮廓区间的圆弧接近于拟合圆，因此对于该段并不需要求确定的角度，只需要对其进行圆拟合处理，从而可以得出该段区间的拟合圆心与直径。第六区段工件轮廓的圆弧图形及拟合图形如图10、图11所示，拟合方程如式(19)～式(21)。

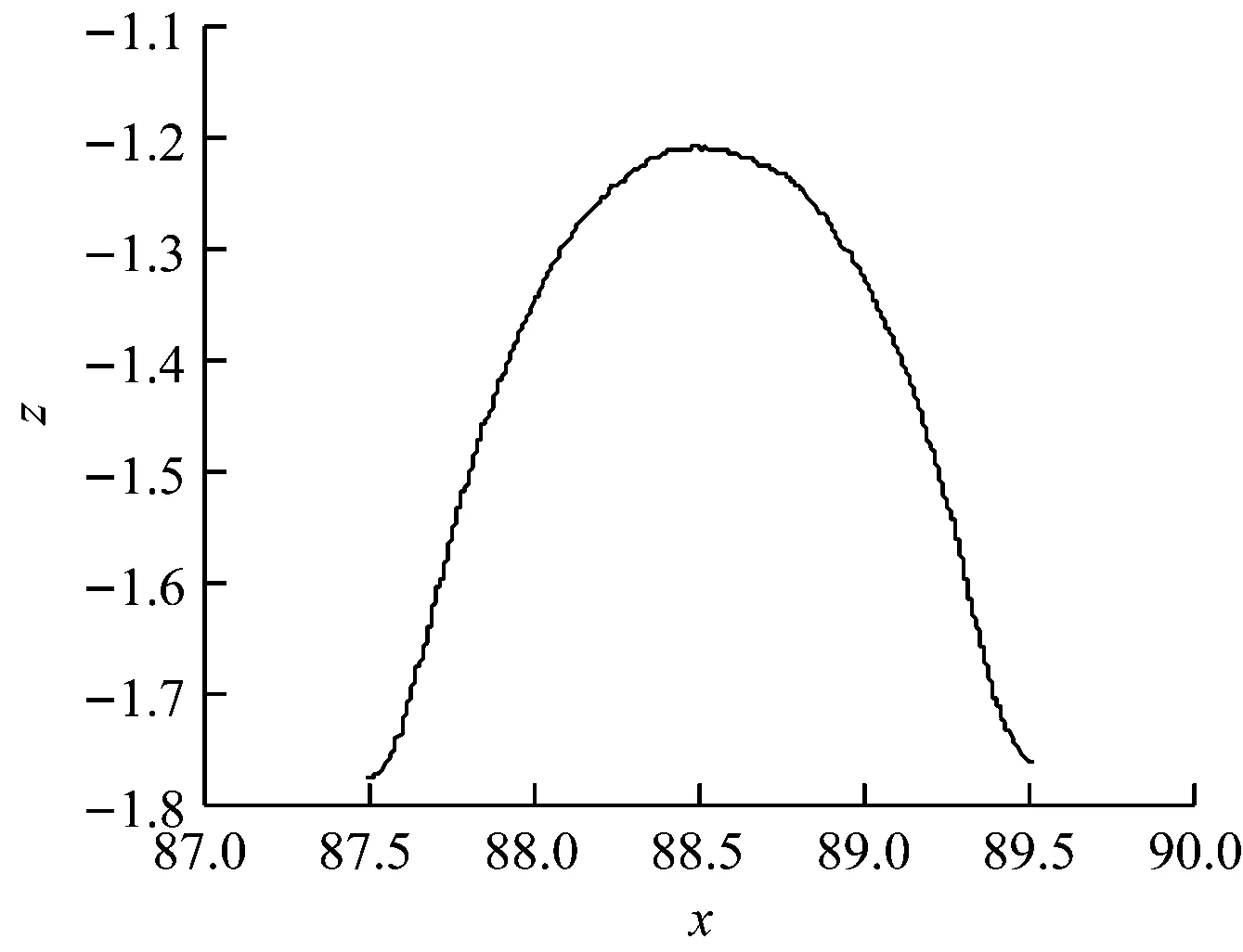
图10 第六段凹形曲线

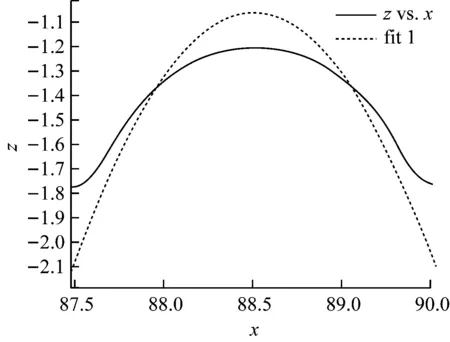
图11 第六段拟合后曲线

拟合方程：

x2+z2-117x-39.69z-75.58=0

(19)

半径公式：

(20)

弧长公式：

d6=arctanθ6×R6

(21)

同理可得，工件轮廓第七区段区间与第八区段区间上的圆弧图形及其拟合曲线图，如图12～图15所示。进而可以求得槽口宽度x11和圆心，连接圆心与弧长的两个端点，由圆的性质得该连接线为圆的半径R，进而可以根据式(22)进一步得到弧长夹角θ。第七区间拟合曲线方程如式(23)～式(25)。

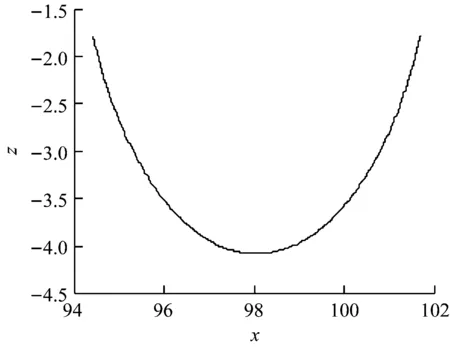
图12 第七段凹形曲线

图13 第七段拟合后曲线

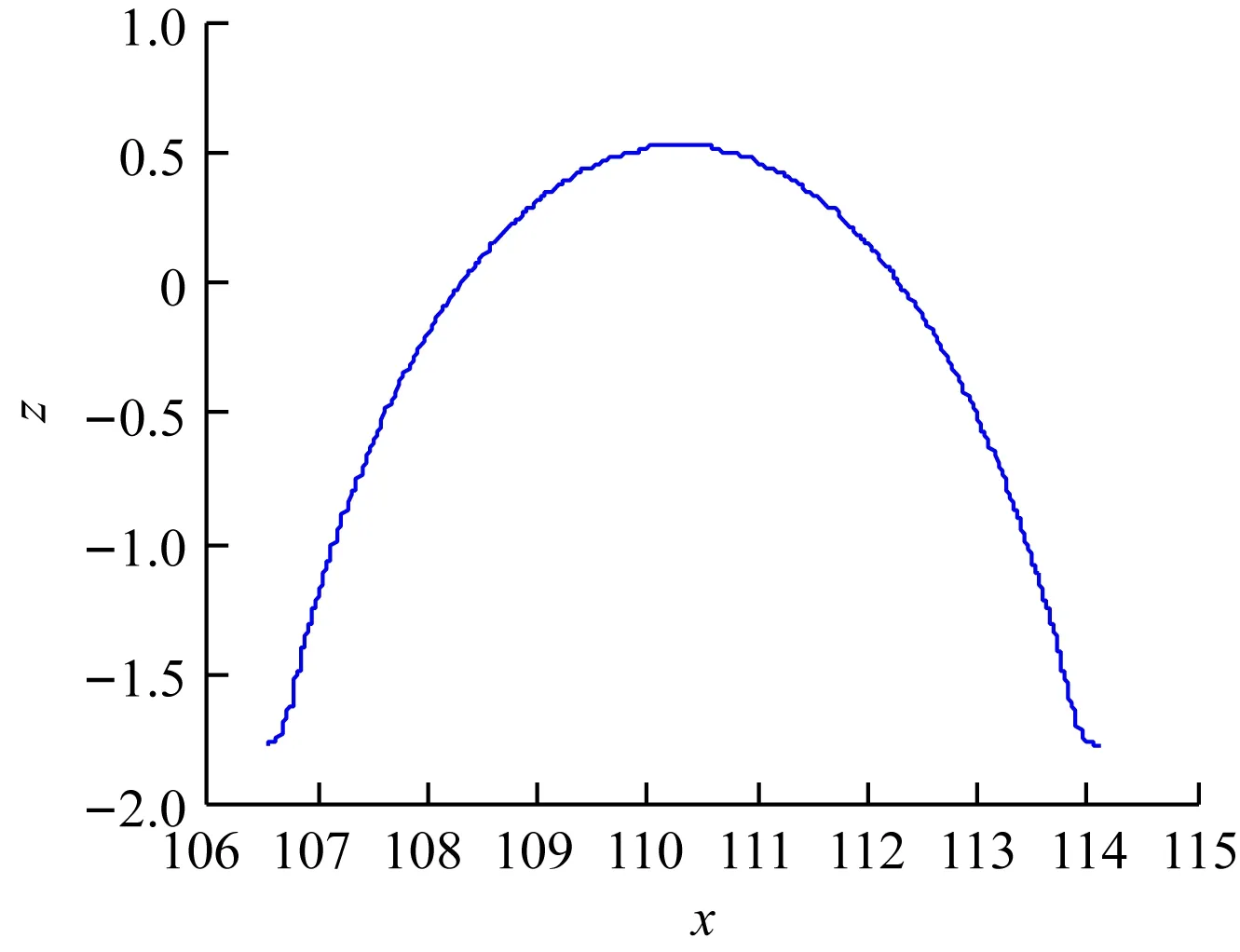
图14 第八段凹形曲线

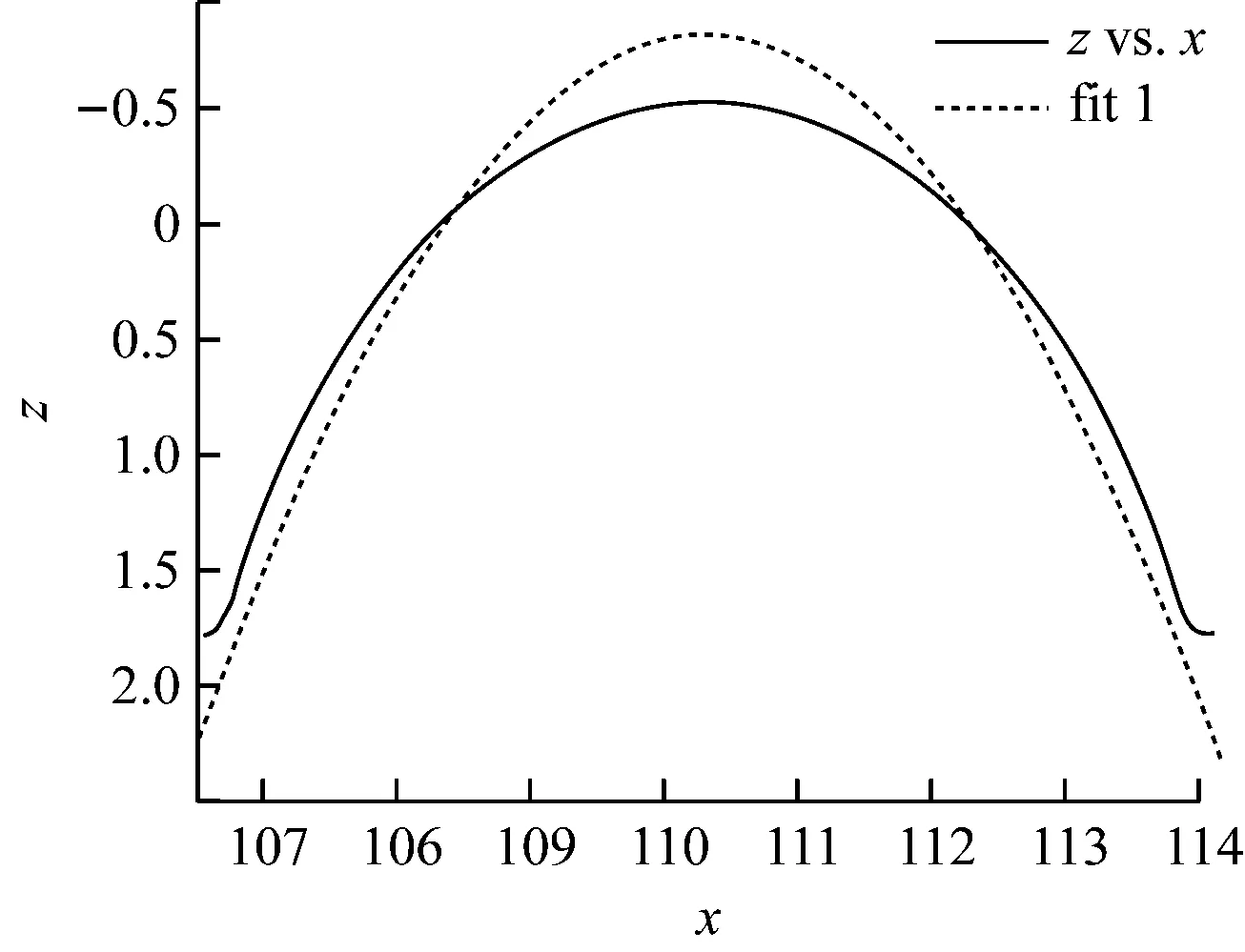
图15 第八段拟合后曲线

(22)

拟合方程：

x2+z2+0.022 38x-9.803z-0.701=0

(23)

半径公式：

(24)

弧长公式：

d7=arctanθ7×R7

(25)

工件轮廓曲线第八区段拟合曲线方程如式(26)～式(28)。

拟合方程：

x2+z2+0.014 8x+1.774z-1.407=0

(26)

半径公式：

(27)

弧长公式：

d8=arctanθ8×R8

(28)

根据式(1)～式(28)可以得到工件轮廓曲线各参数取值，如表1所示。将表1中的参数在图1中进行标注，可以得到含有参数的工件轮廓，如图16所示。

表1 工件轮廓各参数取值

图16 水平状态下工件轮廓曲线图

通过对工件1在水平状态下的轮廓数据分析可知，该工件轮廓模型由圆弧与直线构成，结构复杂，属于典型的非线性系统，很难直接利用分析工具获得其准确的数学模型。因此，本文利用分段模型拟合思想对其模型数据进行分析，进而建立了工件1的轮廓曲线参数修正模型如式(29)：

x2+z2+ax+bz-c=0

(29)

di=arctanθi×Ri

其中，a、b、c为工件轮廓曲线圆弧所在圆方程参数，i为圆弧的标号，Ri为拟合圆的半径，θi为圆弧对应的圆周角，di为弧长。

2.2 工件轮廓倾斜角度的水平校正

在实际工程应用中，由于测试位置的倾斜，可能使得测试数据存在一定的误差。为了消除由于位置倾斜引起的误差，本文根据工件1的倾斜角和水平状态的测试数据，运用数学建模方法，建立轮廓仪测试工件水平校正数学模型：

x=(x-x0)×cosθ-(z-z0)×sinθ+x0

y=(x-x0)×sinθ+(z-z0)×cosθ+z0

(30)

式中，θ为工件模型修正角度。

图17为轮廓仪测试工件1的倾斜曲线图。根据上述校正数学模型，可以得到如图18所示的工件1轮廓线的水平校正曲线图。

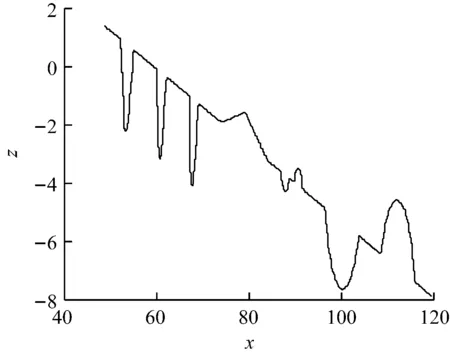
图17 斜率校正前工件轮廓曲线图

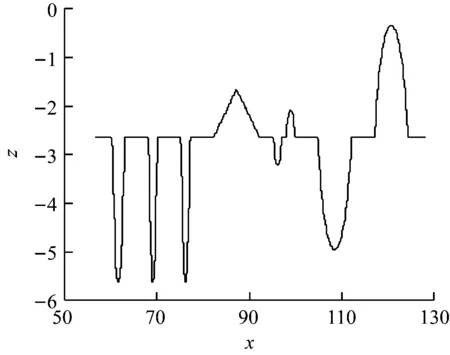
图18 斜率校正后校正斜率图

3 工件轮廓参数修正模型的验证

为验证第二部分中所建立的工件轮廓参数修正数学模型，先通过在不同倾斜角度情况下对工件2的轮廓进行位置和参数的修正，进一步讨论改轮廓修正模型的实用性。

图19～图23的(a)为工件2在不同角度、测量起点和终点等不同位置的多次检测数据。首先利用式(29)中的水平修正模型对其进行水平位置修正，修正结果如图19～图23的(b)所示。

(a)校正前

(a)校正前

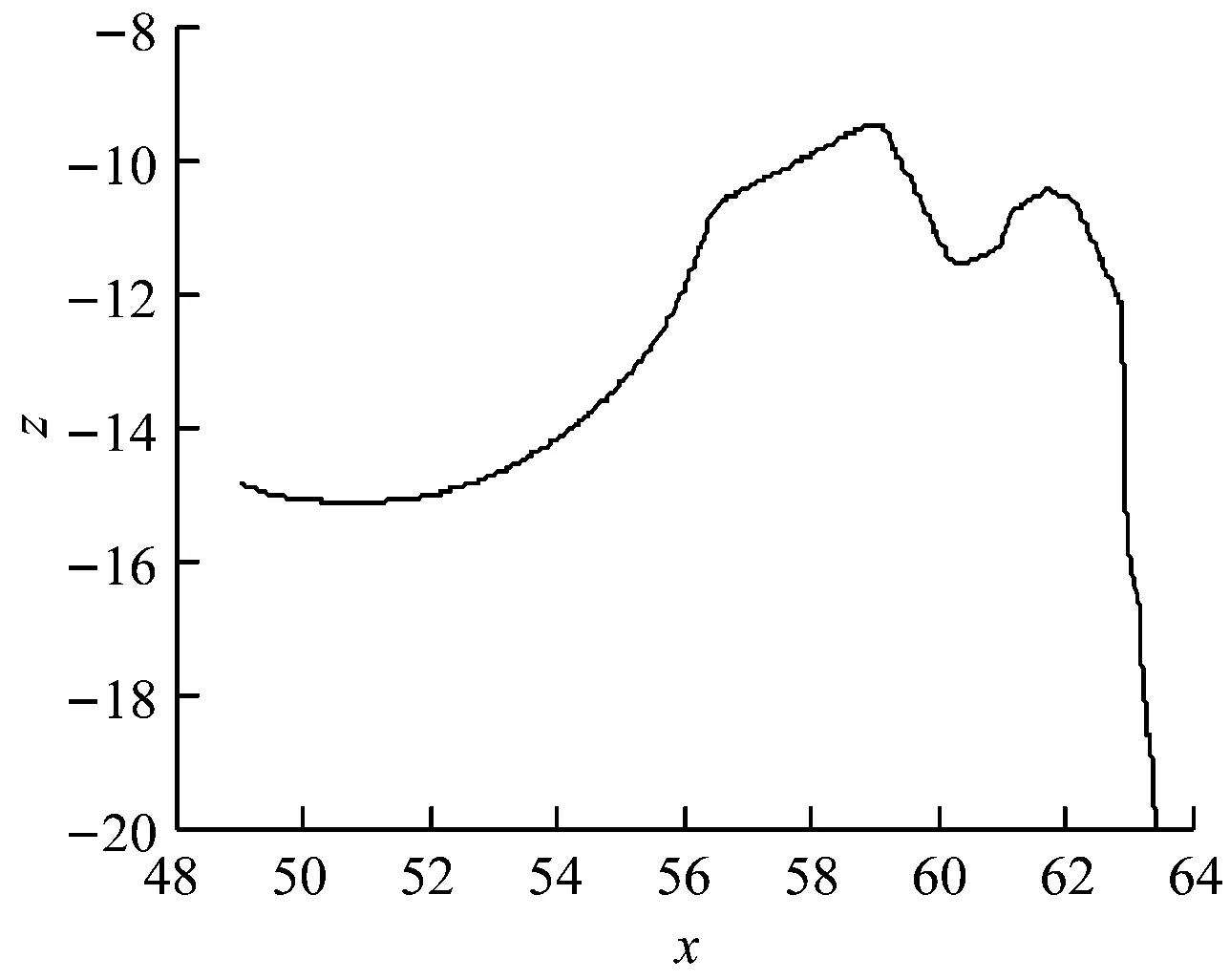
(a)校正前

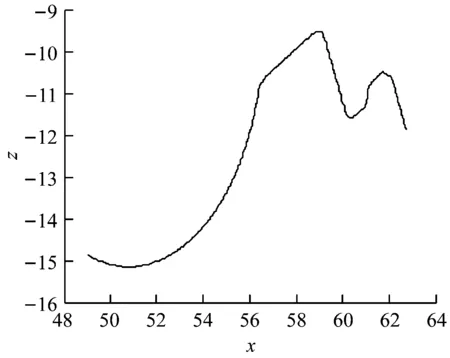
(a)校正前

(a)校正前

对比图19～图23的(b)中工件2在不同测量条件下的测量曲线图，工件2轮廓在不同的测量工况下存在着一定的误差。因此，为进一步获得工件2精确的轮廓曲线，根据数学模型可以对工件2轮廓线中的各参数进行修正，进一步得到工件2的参数如图24所示。

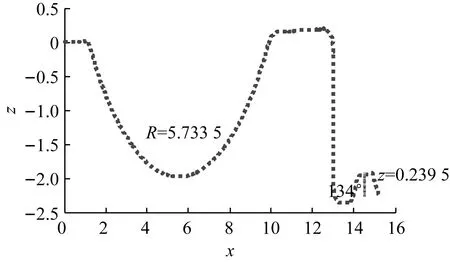
图24 工件2完整轮廓线

在参数条件过程中，主要程序代码如下：

X=A;

n=length(X(:,1));

y=ones(n,1);

b=[rand(1)*1000 rand(1)rand(1)];

fun=inline(’X(:,1).^2+X(:,2).^2+a(1)*X(:,1)+a(2)*X(:,2)+a(3)’,’a’,’X’);

[a,r,J]=nlinfit(X,y,fun,b);

vpa(a,10);

X1=-a(1)/2；

Y1=-a(2)/2；

R=sqrt(a(1)^2+a(2)^2-4*a(3))/2；

4 总结

接触式轮廓仪在机械行业和轴承行业运用十分广泛，轮廓仪的主要优点是可以直接测量一些比较难以测得的零件的表面粗糙程度，而且可以快速测量整个剖面。本文根据工件1的轮廓曲线数据，以数据为先导建立数学模型，利用建立的数学模型对工件2在不同工况下与倾斜角度下的测量数据进行参数修正与水平位置调节，得到了工件2的精确轮廓模型，进一步验证了该模型简单易懂，处理数据能力强，精确度较高。但由于该数学模型在进行数据参数分析时测试数据众多，在原始数据量特别密集的时候，该取点方法还需再做进一步精细化操作。