瞬变电磁长短时记忆网络深度学习实时反演方法

范涛，薛国强，李萍，燕斌，鲍亮，宋金秋，任笑，李泽林

1 中煤科工西安研究院(集团)有限公司，西安 710077 2 中国科学院地质与地球物理研究所 中国科学院矿产资源研究重点实验室，北京 100029 3 西安电子科技大学计算机科学与技术学院，西安 710071

0 引言

瞬变电磁法作为一种低成本的地球物理勘探方法，多年以来一直被用于资源与环境领域(Guo et al., 2020；Fan et al., 2020；Di et al., 2020a).瞬变电磁实测数据一维反演方法，如共轭梯度法、高斯-牛顿法和最小二乘法等线性化反演(孙怀凤等，2019；Maurya et al., 2019；陈卫营等,2017；Li，2016)，也取得了一定的应用效果.实际上，反演问题是非线性、多极值、多参数的，线性化近似在一定程度上会丢失细节信息，尤其是进行较为精细的地质结构探查时，如果初始模型选择不当，极易陷入局部最优解，而非全局最优解，导致线性化反演的结果往往与实际情况相差甚远.

由于地下介质的复杂性，高维反演问题尚未妥善解决(Xue et al., 2020；Luan et al., 2020；Yin et al., 2015)，三维反演方法受限于复杂的三维正演算法，数据量巨大，占用资源过多，反演运算速度缓慢，很难真正投入实际应用(Cox et al., 2012；Oldenburg et al., 2013).因此，粒子群优化算法、差分蚁群算法、模拟退火算法、人工鱼群优化方法、遗传算法和贝叶斯方法等优化方法得到研究和应用(Di et al., 2020b；Li et al., 2021, 2019a；程久龙等，2014)，这些方法对初始模型依赖较小，且不需要计算雅克比矩阵，但仍需要大量正演计算，收敛速度较慢，算法参数的要求比较严格，参数选择不当甚至会使反演出现早熟或是不收敛的情况，反演结果随机性也较大.

神经网络技术也被应用于瞬变电磁反演问题，出现了监督下降法(SDM)、反向传播(BP)算法、深度置信网络算法和剪枝贝叶斯神经网络(PBNN)等(秦善强，2019；Jiang et al., 2016；王秀臣，2006；李创社等，2001)，无需经典反演中的正演计算过程，也无需求解雅克比矩阵，可大大提高反演速度和效率.随着技术的发展，深度神经网络被广泛应用于各个领域，相比于浅层神经网络，其具有更强的表达能力.目前，在电磁反演领域内，全连接网络、卷积神经网络与遗传神经网络是常用的方法(Wu et al., 2021；程久龙等，2020；Li et al., 2019b；王鹤等，2018).然而，目前该研究领域内还存在着数据集构造较为简单，地层情况丰富度较低，模型设计简单对数据时序性利用不足等问题.同时，深度神经网络更容易出现过拟合、收敛速度慢、陷入局部最优等情况.针对上述难点，需要对深度神经网络进行更好的设计，如使用各种基于动量的优化器、加入dropout、使用Layer Normalization机制(Ba et al., 2016)等.

由瞬变电磁数据可以得出其反演问题属于时间序列问题，可使用深度学习中专门解决时序问题的循环神经网络进行处理.长短时记忆网络(Long Short-Term Memory Network，LSTM)是循环神经网络(Recurrent Neural Network，RNN)中的一种特殊模型，它具备RNN的递归属性(Visin et al., 2015)，同时也是RNN的一种改进模型.它具有独特的记忆、遗忘模式，可以灵活地适应网络学习任务的时序特征(Hochreiter and Schmidhuber, 1997).LSTM解决了RNN在长序列训练过程中的梯度消失和梯度爆炸问题，能够充分利用历史信息，建模信号的时间依赖关系(Chung et al., 2014).至今，LSTM已经在各种序列任务取得了巨大成功，例如，机器翻译、语音识别、文本分类等(Ma et al., 2020；Merity et al., 2017；Zhang et al., 2016；Cho et al., 2014).

本文开展基于LSTM的瞬变电磁反演算法研究，在提高反演精度的前提下进一步实现实时成像.首先介绍本文采用的LSTM方法理论和在此基础上实现的瞬变电磁反演算法，然后将本文算法应用于一维和三维数值模拟数据的反演中以检验本文算法的有效性，并对比本文方法与传统反演方法的计算耗时.

1 长短时记忆网络(LSTM)

LSTM网络由输入层、输出层和隐藏层构成，单元内部结构如图1所示.

图1 LSTM单元内部结构Fig.1 Internal structure of the LSTM unit

LSTM单元的工作流程如下：每一个时刻，LSTM单元通过3个门接受当前状态xt和上一时刻LSTM的隐藏状态ht-1这两类外部信息的输入.此外，每一个门还接收一个内部信息输入，即记忆单元的状态Ct-1.接收输入信息后，每一个门将对不同来源的输入进行运算，并且由其逻辑单元决定其是否激活.输入门的输入经过非线性函数的变换后与遗忘门处理过的记忆单元状态进行叠加，形成新的记忆单元Ct.最终，记忆单元状态Ct通过非线性函数的运算和输出门的工台控制形成LSTM单元的输出ht.

各变量之间的计算公式见(1)—(5)式：

it=σ(Wxfxt+Whfht-1+bf),

(1)

ft=σ(Wxfxt+Whfht-1+bf),

(2)

Ct=ftCt-1+ittanh(Wxcxc+Whfht-1+bc),(3)

ot=σ(Wxoxt+Whoht-1+bo),

(4)

ht=ottanh(Ct),

(5)

式中：Wxc、Wxi、Wxf、Wxo为连接输入信号xt的权重矩阵；Whc、Whi、Whf、Who为连接隐含输出信号ht的权重矩阵；Wci、Wcf、Wco为连接神经元激活函数输出矢量Ct和门函数的对角矩阵；bi、bc、bf、bo为偏置向量；σ为激活函数，通常为tanh或sigmoid函数.

算法的基本思路为：先将LSTM网络按照时间顺序展开为一个深层的网络，然后使用经典的误差反向传播(back propagation，BP)算法对展开后的网络进行训练，其示意图如图2所示.

图2 LSTM网络重复模式Fig.2 LSTM network duplication mode

2 序列到序列(Seq2seq)模型

2.1 Seq2seq模型简述

序列到序列(Seq2seq)模型为自然语言处理(natural language processing，NLP)领域的经典模型，其中最常用的Encoder-Decoder模型如图3所示.encoder接收每个时间步的输入信息(X1,X2,X3,X4)，通过encoder将其编码为一个表示向量，称为context vector(图中用C表示)，然后交给decoder来进行解码.decoder根据context vector与上个时间步的输出信息产生每个时间步的输出(Y1,Y2,〈EOS〉)，其中，〈g〉代表输入序列的结束与输出序列的开始，〈EOS〉代表输出序列的结束，是一个事先定义在输出字典里的标志，循环网络在产生此标志后，不再进行下一时间步的操作.

图3 Encoder-Decoder结构(a)Encoder结构(b) Decoder结构Fig.3 Encoder-Decoder structure (a) Encoder structure (b) Decoder structure

2.2 free running与teacher forcing

在NLP领域的机器翻译问题中，decoder部分每一时间步的输出代表着词袋中每一个词的预测出现概率，通常会将概率最大的词作为翻译的结果，并将相应的词嵌入向量作为下一时间步的输入之一，这种结构通常被称为free running，此时Seq2seq内部结构如图4所示.

图4 Free running机制图Fig.4 The free running mechanism diagram

为了提升训练速度，常常使用teacher forcing(Williams and Zipser, 1989)机制，在decoder端，使用真实的目标文本作为每一时间步的输入.每一步根据当前正确的输出词和上一步的隐状态，来预测下一步的输出词，Seq2seq的内部结构如图5所示.

图5 Teacher forcing机制图Fig.5 The teacher forcing mechanism diagram

2.3 Attention机制

随着输入序列的不断增长，使用上述方法的序列到序列模型的表现会越来越差，于是人们提出了注意力(attention)机制，此方法使decoder的每个时间步的输出可以根据不同的context vector生成，在decoder的不同时间步，产生对输入序列的不同关注重点.

假设共有n个时间步的输入，encoder第i个时间步的输出为ei，decoder第j-1个时间步的输出为qj-1，则decoder第j个时间步的context vectorCj的计算公式如式(6)到式(8)所示.

(6)

(7)

(8)

Attention机制模型如图6所示.decoder每个时间步使用不同的Cj.

图6 Attention机制图Fig.6 The attention mechanism diagram

3 基于LSTM的瞬变电磁反演

在模型训练环节，将正演得到视电阻率数据输入模型进行训练，并通过超参数优化提升模型性能，之后运用评估指标进行模型评估.最终，得到训练、优化完成的模型用于预测未知的地层结构，即使用模型完成瞬变电磁实时反演成像.

3.1 模拟数据准备与评价指标

模拟数据主要用来在理论层面上展示算法的可用性.而由于实际地层构成情况十分复杂，则需要根据实际面临的反演问题对模拟生成的训练数据进行调整，并随后在实测数据上进行反演测试.

本文使用基于汉克尔变换和余弦变换的瞬变电磁一维正演程序生成样本集.在模拟数据实验中，将正演模拟数据分为train(训练集)、eval(验证集)、test(测试集)三部分.在检测数据实验中，使用人工指定参数、通过三维数值模拟生成的模型数据作为额外的测试数据.检测数据主要用来验证反演算法对复杂模型的适用性.

通过三个指标评价算法的效果，分别是正演曲线点相对误差(FPRE)、反演折线面积相对误差(BARE)和反演折线点相对误差(BPRE).

FPRE是通过在目标地层结构与预测地层结构分别正演出的曲线上相应取出N个点，计算它们的平均相对误差得出的，它衡量了两个正演曲线的拟合程度.具体计算公式如式(9)，其中pi为预测地层结构的正演曲线上的第i个点，ti为目标地层结构的正演曲线上的第i个点：

(9)

BARE是通过计算代表目标地层结构与预测地层结构的折线间的相对面积误差得出的，它通过面积的差值比衡量了两个地层结构折线的相似程度.具体计算公式如式(10)，其中Stp指的是两个折线之间围城的面积，St指的是目标地层结构折线与x轴(x轴为深度，y轴为电阻率)围成的面积：

(10)

BPRE是通过在代表目标地层结构与预测地层结构的折线上相应取出N个点，计算它们的平均相对误差得出的，它通过点之间的差值比衡量了两个地层结构折线的相似程度.具体计算公式如式(11)，其中pi为预测地层结构折线上的第i个点，ti为目标地层结构折线上的第i个点：

(11)

3.2 Seq2seq网络设计

反演算法整体框架使用Seq2seq模型，包含encoder，decoder，attention三部分，整体结构如图7所示.

Encoder部分的主要目的是将input的信息用一个向量表示出来，本文所使用的encoder为双向LSTM网络.在进行地层预测时，需要综合各个地层的信息，最终的地层预测结果由前面若干输入和后面若干输入共同决定，因此使用双向LSTM网络以使得预测结果更加准确.

Encoder的详细结构如图8所示.

图7 反演算法整体框架Fig.7 Overall framework of the inversion algorithm

图8 Encoder架构图Fig.8 Encoder Architecture diagram

早期的Seq2seq模型没有使用attention机制，在输入序列input较长或者包含信息较多时，会丢失很多信息，attention机制可使decoder在翻译时能够依靠包含不同input信息侧重点的context vector.本文使用Bahdanau Attention(Bahdanau et al.，2016)，主要计算过程如下：

(1)第i个target上下文向量ci会根据input的隐藏状态加权求和得到：

(12)

(2)其中，对于每个hj的系数αij根据下式得到：

(13)

其中eij=a(si-1,hj)，si-1为输出序列的上一个隐状态，a将decoder的上一个隐状态si-1和encoder的隐状态hj作为输入，计算出一个xi,yj对齐的值eij(此值可以衡量输出序列和输入序列的对应情况，越对应，权重越高，即注意力高)，再归一化得到权重.

Attention机制的架构如图9所示.

图9 Attention架构图Fig.9 The attention architecture diagram

Decoder部分每个时间步的输入中不包括上一时间步的输出，即本文的算法在free running结构的基础上进行了适应性修改.此做法是为了缓解过拟合，增强模型的泛化能力.在机器翻译问题中，decoder每一时间步的输出是词的选中概率，算法需要根据此概率选出每一时间步的真正输出词汇，然后将其相应的词嵌入向量作为下一时间步的输入，从而为模型补充被选词的信息.而针对瞬变电磁反演问题，decoder的每一个时间步的输出是实数，它们是LSTM的输出htot经过后续计算得到的，同时ht也作为隐藏状态传入到了下一时间步中，所以decoder的每一个时间步中不需要重复地输入信息.这样做一方面减少了网络的参数量，另一方面避免了从输入项中再次引入误差.

Decoder的架构如图10所示.

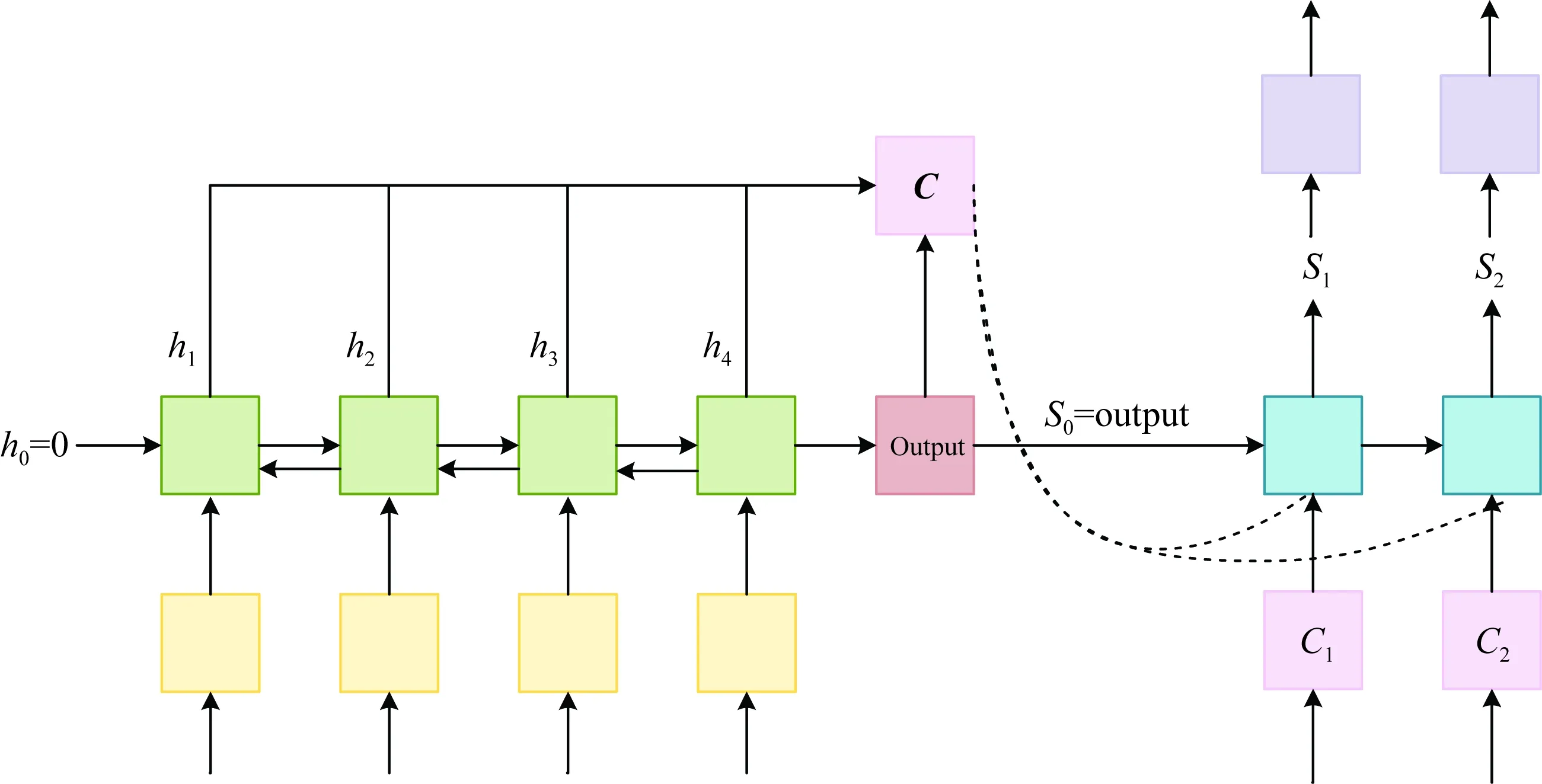
图10 Decoder架构图Fig.10 The decoder architecture diagram

3.3 损失函数设计

损失函数包含三部分，分别为：电阻率损失、厚度损失和深度损失，公式如式(14)所示.电阻率损失、厚度损失分别针对电阻率、地层厚度这两个预测目标进行拟合.同时，为了避免每个地层的厚度预测误差累积导致较深层地层的位置发生较大偏移，加入深度损失，对近地层的厚度预测进行校正：

loss=lossρ+losst+lossd.

(14)

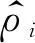
(15)

(16)

(17)

d1=t1,

(18)

di=ti+di-1,i=2,…,L,

(19)

(20)

(21)

3.4 超参数设置

本文所使用的Seq2seq模型的超参数以及训练过程的超参数如表1所示.

由于针对较复杂的地层，模型训练需要较多的数据，为了平衡正演样本生成时间成本和模型预测的准确性，设定训练、验证和测试样本的比例为 0.9∶0.05∶0.05.

表1 超参数设置表Table 1 Over the parameter setting table

4 随机模拟数据训练和测试

4.1 三层模型

本节通过使用表2所示的参数生成3个地层的正演模拟数据.

表2 三层模型参数设置表Table 2 The parameter setting table of the three-layer model

本节实验最终的loss函数下降趋势如图11所示.从图中可看出，loss不断下降至收敛，且无过拟合现象.这说明该模型对三层地层的数据具备较强的拟合能力.

图11 三层模型loss下降趋势曲线图Fig.11 The loss decay curve of the three-layer model

随机选取了9个测试数据，本模型对地层分布的反演结果及目标结果图12所示.由于学习率衰减方式为阶梯式衰减，如表1所示，所以loss下降趋势呈阶梯式下降，符合预期.从图中可看出，反演结果中绝大部分的曲线都完全吻合，少部分地层的厚度和电阻率大小有一些误差，但均处于可接受范围内.因此，基于时间序列的反演模型具有学习出三层地层形态的能力.

模型的三个衡量指标结果如表3所示.

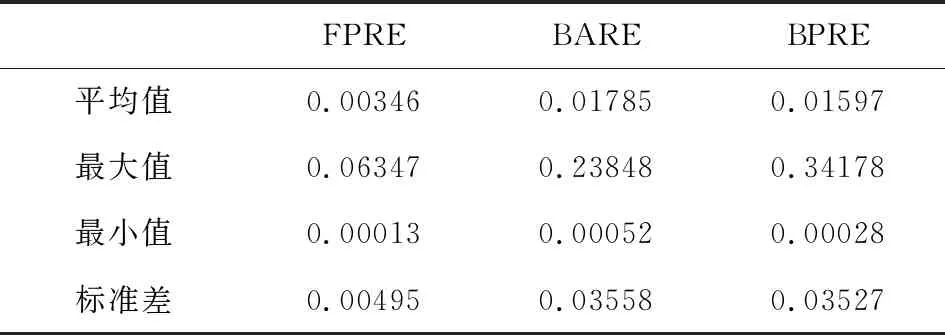
表3 三层模型衡量指标值表Table 3 Table of three-layer model measures

4.2 五层模型

本节通过使用表4所示的参数生成5个地层的正演模拟数据.

表4 五层模型参数设置Table 4 Five-layer model parameter settings

图12 三层模型部分反演结果与目标对比(a) 模型17; (b) 模型24; (c) 模型75; (d) 模型94; (e) 模型131; (f) 模型183; (g) 模型206; (h) 模型277; (i) 模型349.Fig.12 The partial inversion results of the three-layer model are compared with the target(a) Model 17; (b) Model 24; (c) Model 75; (d) Model 94; (e) Model 131; (f) Model 183; (g) Model 206; (h) Model 277; (i) Model 349.

本实验最终的loss函数下降趋势如图13所示.从图中可看出，loss不断下降至收敛，仅出现了轻微的过拟合现象.这说明该模型对五层地层的数据仍具备较强的拟合能力.

图13 五层模型loss下降趋势曲线图Fig.13 The loss downward trend curve of the five-layer model

同样随机选取了9个测试数据，本模型对地层分布的反演结果及目标结果图14所示.从图中可看出，随着地层数的增加，虽然五层的反演结果相较于三层的结果准确度有所下降，但是Seq2seq模型的反演结果依然能够较好地预测出地层厚度和电阻率的整体变化趋势，基本能够和目标地层情况吻合，说明该模型在五层地层数据上依然比较稳定.且从图14中可以看出，深度的反演误差相对于厚度和电阻率的反演误差较小，从而印证了loss函数中深度loss的设计使得模型在浅层地层厚度有预测偏差时，对后续深层地层的预测不会产生较大的影响.

模型的三个衡量指标结果如表5所示.从三个评价指标中可看出，与三层数据的训练结果相比较，五层数据的测试效果出现下降，这说明面对复杂的地层分布情况，模型需要扩充容量或进行针对性设计.

图14 五层模型部分反演结果与目标对比(a) 模型59; (b) 模型87; (c) 模型165; (d) 模型216; (e) 模型269; (f) 模型323; (g) 模型485; (h) 模型540; (i) 模型634.Fig.14 The partial inversion results of the five-layer model are compared with the target(a) Model 59; (b) Model 87; (c) Model 165; (d) Model 216; (e) Model 269; (f) Model 323; (g) Model 485; (h) Model 540; (i) Model 634.

表5 五层模型衡量指标值Table 5 Measurement values of the five-layer model

5 检测数据验证

5.1 均匀空间单一低阻异常模型

首先设置一个简单地电模型检验反演模型的准确性，模型设计如图15a所示，背景为均匀半空间，电阻率为500 Ωm，异常体在模型中心，电阻率为10 Ωm，异常体埋深为50 m，厚度为50 m，发射线框边长100 m，测点共布置3个，异常体上方1个，两侧各1个.

对图15a中的测点数据进行反演，可得如图15(b、c)所示的反演结果.对比(b)(c)两图可以看出，OCAMM反演结果尽管能够反演出测区中部有一低阻异常区，横向边界也很清晰，但深度方向的边界分辨率较低，上边界大约在30 m，下边界无法分辨，异常中心的电阻率值也要明显高于设置值，且异常体两侧的正常测点也表现出了轻微的高阻-低阻-高阻分层特征，与设置的均匀背景不符；而Seq2seq模型反演结果中，低阻异常体的边界非常清晰，与设置位置完全吻合，异常体的电阻率值与设置值相同，异常体两侧的正常测点的电阻率也与设置的均匀背景值一致，仅异常体下方的电阻率值比设置的背景值略低.

图15 均匀空间模型示意图和反演结果(a) 模型示意图; (b) OCAMM反演结果; (c) Seq2seq模型反演结果.Fig.15 Model schematic diagram and inversion results(a) Model schematic; (b) OCAMM inversion results; (c) Seq2seq model inversion results.

本次测试，OCAMM反演结果用时约16.34 min，Seq2seq模型反演用时小于1 s.

以该模型为基础，通过对正演数据加入不同比例的噪声，检测Seq2seq模型反演算法的适用性，结果如图16所示.图中可以看出，即使噪声增加到20%，对与背景值差异较大的异常体边界的反演结果依然较为准确，但噪声仅增加2%，均匀背景中就开始出现不均匀的现象，噪声增加至10%，均匀背景就表现出明显Q型地层特征，且异常体上部地层电阻率也与两侧背景值出现了肉眼可见的差异，在噪声进一步增加后，这种表现较为稳定.因此综合来看，当正演数据中噪声占比达10%以上时，反演成果中与背景值差异较大的显著异常仍有较大的可信度，但与背景值差异较小的异常的置信度需要调低.

图16 加噪声正演数据的反演结果对比(a) 无噪声; (b) 噪声占比2%; (c) 噪声占比5%; (d) 噪声占比10%; (e) 噪声占比15%; (f) 噪声占比20%.Fig.16 Comparison of inversion results for noisy forward modeling data(a) No noise; (b) Noise accounts for 2%; (c) Noise accounts for 5%; (d) Noise accounts for 10%; (e) Noise accounts for 15%; (f) Noise accounts for 20%.

5.2 复杂地层高低阻异常交错模型

为进一步验证Seq2seq模型反演算法对复杂地电模型的反演效果，设计了如图17a的模型.图中背景电阻率为300 Ωm，中间含断层的煤层层位电阻率为700 Ωm，厚度为200 m，左侧宽度为11个测点，右侧宽度为17个测点，左上角的低阻异常电阻率为10 Ωm，埋深50 m，厚度100 m，宽度为4个测点，左下角的高阻异常电阻率为1000 Ωm，埋深500 m，厚度200 m，宽度为2个测点，右上角的高阻异常电阻率为1000 Ωm，埋深50 m，厚度100 m，宽度为2个测点，右下角的低阻异常电阻率为10 Ωm，埋深400 m，厚度300 m，宽度为4个测点.发射线框边长400 m.

图17 复杂地层模型示意图和反演结果(a) 模型示意图; (b) OCAMM反演结果; (c) Seq2seq模型反演结果.Fig.17 Model schematic diagram and inversion results(a) Model schematic; (b) OCAMM inversion results; (c) Seq2seq model inversion results.

对图17a中的测点数据进行反演，可得如图17b、c所示的反演结果.对比(b)(c)两图可以看出，OCAMM反演结果对煤层、断层和4个异常体均有一定反映，但埋深、厚度和边界均不准确、不清晰，尤其是异常埋深和下边界，均与设置值不符，下部两个异常体的下边界甚至无法反映，各个部分的电阻率也与设置值差异较大；而Seq2seq模型反演结果中，煤层、断层和4个异常体的边界反映均较为清晰，尤其是埋深、厚度、上下界面都与设置值基本吻合，仅煤层厚度存在一定误差，而较宽的两个异常体，中间和两侧的厚度及上下边界也有一定误差，此外，除低阻异常体外的其他区域，电阻率值较设置值均偏低，但总体来看，反演精度显著高于OCAMM反演结果，与预设模型吻合度较高.

本次测试，OCAMM反演结果用时约30.58 min，Seq2seq模型反演用时小于1 s.

6 结论

本文基于长短时记忆网络(LSTM)结合瞬变电磁正演算法，成功实现了可实时成像的高精度瞬变电磁反演.数万组以上随机正演模型的反演结果表明，Seq2seq模型的反演算法计算精度较高，但随着地层层数的增加，会出现一定的过拟合现象，需要扩充样本库容量或进行针对性正演模型设计.三维数值模拟模型的反演结果表明，Seq2seq模型的反演算法精度和速度都显著优于传统的OCCAM反演方法，尤其是对于复杂模型，Seq2seq模型的反演结果能准确反映多个异常体和地层的边界位置、电阻率差异，反演速度更是达到实时化水平.本文的反演结果已经证实了基于LSTM网络的Seq2seq模型相较于传统反演方法的优越性，但是瞬变电磁三维反演仍是业界一个非常具有挑战性的问题，基于Seq2seq模型的三维三分量反演算法将是我们未来的重点研究方向.