基于反电动势谐波分析的FSCW-PMSM失磁故障诊断
徐蕴镠, 李天乐, 余军威, 黄旭聪
(1.国网宁波供电公司,浙江 宁波 315000;2.华中科技大学 电气与电子工程学院,湖北 武汉 430074)
0 引 言
随着永磁同步电机(PMSM)的广泛应用,电机失磁故障已成为业界重点关注的问题。当电机的永磁体遭受物理损伤、高温应力、反向磁场和老化时,都将导致永磁体材料强度降低,进而引发失磁故障。一旦失磁故障发生在运行的设备上,将带来巨大的经济损失和安全威胁[1]。例如,对于电动汽车的轮毂电机,失磁故障会导致汽车失控;对于大型发电机组的副励磁机,失磁故障会降低发电机组输出功率的质量,同时影响供电的可靠性。
针对永磁电机的失磁问题,目前最常采用的解决方法是从电机设计与磁路优化角度出发[2-4],降低失磁风险。但对于运行电机发生的失磁故障,则往往要等故障产生恶劣影响了才会停机检查。为尽快消除故障隐患,确保电机的安全运行,有必要开展永磁电机失磁故障在线监测与诊断研究[5]。
为实现失磁故障监测与诊断,国内外学者在电气特征分析、智能算法、磁链观测器等方面开展了大量研究。文献[6]通过零序电压分量监测失磁故障,但需额外引出中性点;文献[7]利用零序电流分量监测三角形连接的永磁同步电机,但其分析结论难以有效解释故障现象;文献[8]对电机注入额外信号以区分失磁故障和气隙偏心故障;文献[9]提出一种基于Vold-Kalman阶次追踪滤波器的转子故障监测方法,但只能监测整体失磁;文献[10-11]利用深度学习、神经网络等智能算法诊断电机失磁故障;文献[12-13]则提出通过搭建磁链观测器来监测永磁体状态。
近年来,分数槽集中绕组(FSCW)PMSM因其转矩密度高、弱磁性能好、齿槽转矩小和效率高等特点,在电动汽车、航空航天等工程领域受到了广泛关注[14-16]。为实现FSCW-PMSM局部失磁故障监测与诊断,需要准确获得其单槽反电动势和单相反电动势特征谐波的变化规律。本文首先建立了电机磁动势和单槽反电动势在失磁故障下的数学模型,接着结合单槽反电动势的谐波幅值特征和分数槽集中绕组的绕组系数,推导得到单相反电动势各谐波分量的幅值特征,验证了利用单相反电动势谐波变化特征诊断失磁故障的可行性。最后,基于一台20极24槽内置式永磁同步电机(IPMSM)的样机参数建立二维有限元模型开展电磁仿真分析,获得单相反电动势特征谐波的变化。
1 电机关键设计参数
本文分析使用的FSCW-PMSM参数如表1所示,其基本结构如图1所示。
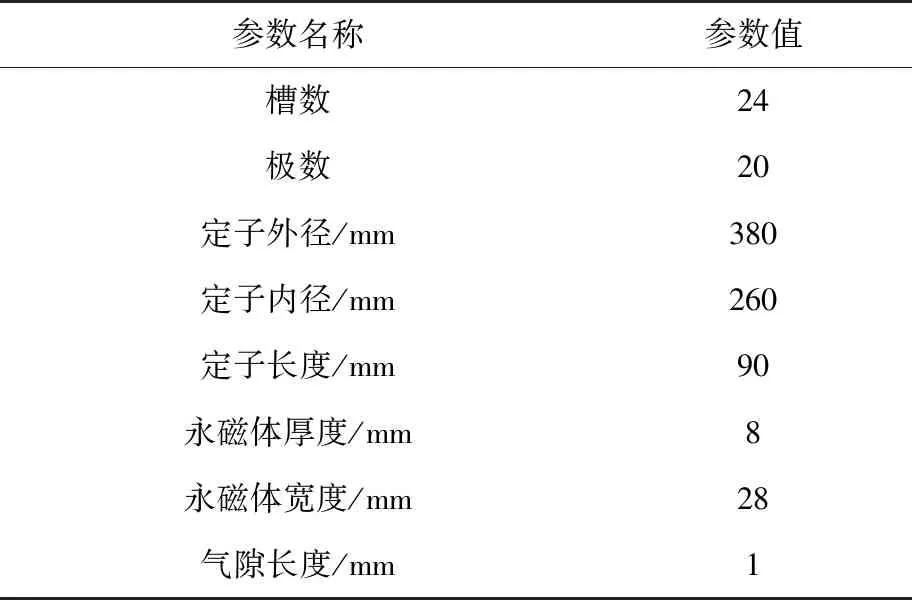
表1 FSCW-PMSM的关键设计参数

图1 电机基本结构
对于三相电机,通常定义其每极每相槽数q如下式所示:

(1)
式中:Zs为槽数;p为极对数;N和D互素。在本文中,q=2/5,N=2,D=5。
同时定义单元电机数量Nt如下:

(2)
2 数学模型
2.1 失磁模型
正常运行电机的理想磁动势可由下式表示:
Fr(θ,t)=Frm(2πfet-θ)
(3)
式中:Frm为磁动势基波幅值;fe为电机基频;θ为初始电角度。
假定其中一块永磁体发生失磁,磁动势波形可看作从正弦波中减去特定波形,如图2所示[17]。

图2 局部失磁故障下的磁动势波形
发生失磁故障后,磁动势变为
F′r(θ,t)=Fr(θ,t)-y(t)
(4)
式中:y(t)为永磁体失磁导致的磁动势削除部分。
y(t)又可看作一正弦波与脉冲波x(t)的乘积。对x(t)/Frm进行傅里叶展开得到:
n=1,2,3,…
(5)
因此,y(t)/Frm可展开为
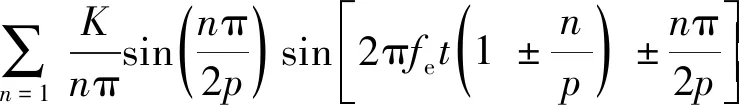
(6)
式中:K为剩余磁密与正常磁密之比。
根据式(6)可推导出发生局部失磁故障时的单槽反电动势如下:

(7)
式中:Eslot为正常情况下单槽反电动势的基波幅值。
根据式(7),可以得到新增单槽反电动势谐波频率如下[18]:

(8)
此外,当不止一块永磁体发生失磁故障时,新增单槽反电动势谐波频率仍满足式(8)。
2.2 绕组系数影响
相比单槽反电动势的变化结论,工程中人们更关心单相反电动势在故障下的变化规律。为获得单相反电动势谐波分量的特性,需要考虑包括绕组分布系数和绕组节距系数在内的绕组系数。
绕组分布系数和绕组节距系数通常分别由以下公式计算得到[19-20]:

(9)

(10)
式中:v为谐波极对数;θ0为相邻槽的电角度;τ为极距;y1为节距。
基于单槽反电动势的谐波幅值和分数槽集中绕组的特征绕组系数,即可计算得到单相反电动势谐波的具体数值:
Ephase,v=kyvkqvpqEslot,v
(11)
式中:Ephase,v和Eslot,v分别为单相反电动势和单槽反电动势谐波分量的幅值。
为获得分数槽集中绕组系数的确切表达式,图3给出单元电机中正槽的空间分布情况,图中1、J2、J3、…为正槽编号,X为一整数,Xθ0表示单元电机中相邻极下的槽间距。

图3 各槽号的空间分布情况
X可由下式描述[21]:

(12)
显然,D和X同为奇数。因此绕组分布系数可改写为如下形式:
kqv=sin{vDX·30°+[1+(-1)vD]·45°}·

(13)
式(13)中,v为
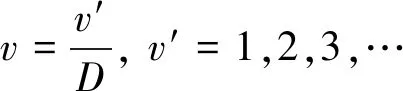
(14)
据式(13)可知,若vD为偶数,则kqv为0。因此,当局部失磁故障发生时,新增单相反电动势谐波频率仅为
fdemag=vfe
(15)

(16)
根据前述各计算参数的计算过程得到文中分析使用的20极24槽FSCW-PMSM的关键计算参数,见表2。

表2 FSCW-PMSM的关键计算参数
3 有限元分析
在有限元仿真软件中开展单个永磁体在不同失磁程度下的电机反电动势分析,运行工况假定为额定转速2 500 r/min的空载情况。
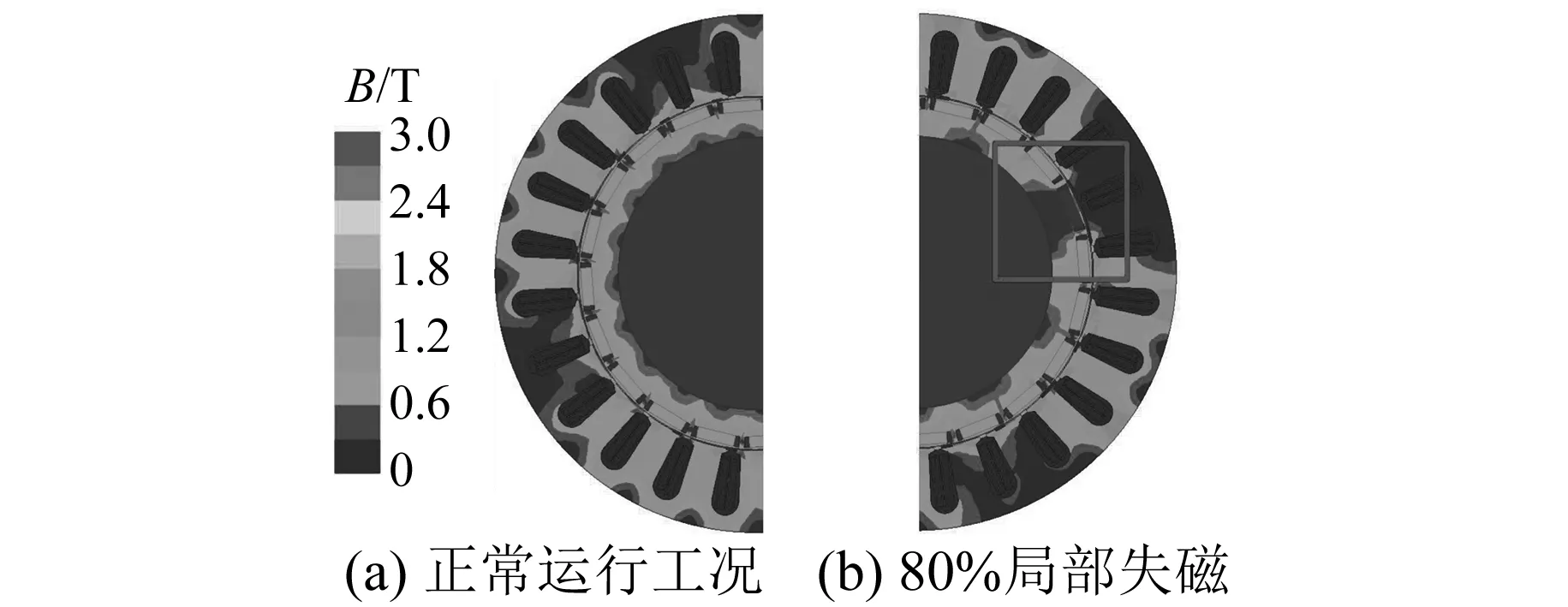
图4 磁密云图对比
图4为正常运行工况和单个永磁体80%局部失磁故障下的磁密云图对比。图4(b)所示方框内为失磁永磁体,可以明显看出气隙磁密低于圆周其他位置。图5分别为气隙磁密、单槽反电动势和单相反电动势在80%局部失磁下的谐波频谱情况,可以看出磁密谐波频率和单槽反电动势谐波频率为fe(1±n/p),与式(8)推导结论一致,而单相反电动势谐波频率为vfe,v=(1,3,5,…)/D,与式(15)、式(16)推导结果一致。
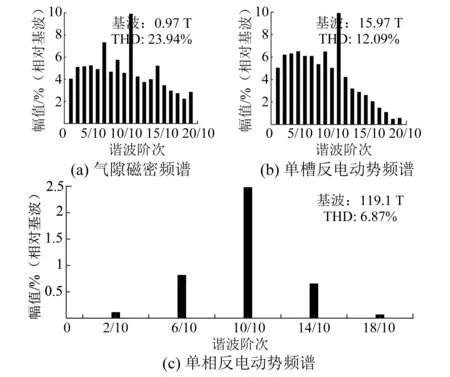
图5 局部失磁下的谐波频谱
通过有限元分析和理论推导分别得到单槽反电动势,其波形对比如图6所示,结果证明单槽反电动势公式推导的准确性。

图6 有限元分析和理论推导下的单槽反电动势对比
80%失磁故障和正常状态下的单相反电动势波形对比如图7所示。由图7可知难以凭幅值区分正常态和故障态,也说明了谐波分析的必要性。

图7 80%失磁故障和正常状态下的单相反电动势波形对比
结合单槽反电动势各分量幅值和绕组系数,可通过式(11)得出单相反电动势各分量。表3为单相反电动势各分量的计算结果和仿真结果,其对比结果证明了由式(11)计算得到的单相反电动势谐波与通过有限元仿真得到的结果一致,验证了式(9)~式(11)的正确性。

表3 单相反电动势各分量理论计算和仿真结果对比
为监测故障的严重程度,对不同故障程度下的单相反电动势谐波进行了分析。表4为不同失磁故障程度下单相反电动势的特征谐波大小。

表4 不同失磁程度下单相反电动势特征谐波幅值 V
随着故障的加剧,单相反电动势特征谐波显著增加,基波分量则线性减小。图8和图9为故障程度加深时各谐波分量和基波分量的拟合曲线。

图8 故障程度加深时各谐波分量的拟合曲线

图9 故障程度加深时基波分量的拟合曲线
此外,对不同数量永磁体失磁时的单相反电动势进行分析,假定失磁永磁体相邻。表5为不同数量永磁体发生失磁故障下的特征谐波幅值,图10为单相反电动势谐波分量随失磁永磁体数量增加的变化情况,图11为基波分量的变化情况。
单相反电动势的特征谐波的大小随故障数量增大呈周期性变化。当失磁永磁体的数量为5(即第2节中定义的D)的倍数时,各谐波幅值最低。同时,当失磁永磁体数量接近5的倍数间的中间数时,各谐波幅值最高。而基波幅值则随失磁永磁体数量的增大而几乎线性下降。

表5 不同数量永磁体失磁故障下的谐波幅值 V

图10 失磁永磁体数量增大时谐波拟合曲线

图11 失磁永磁体数量增大时基波拟合曲线
综上,单相反电动势谐波分析能被有效用于FSCW-PMSM的失磁故障诊断。
4 结 语
通过对局部失磁故障下等效气隙磁密开展傅里叶分析,从理论上得到单槽反电动势的特征谐波。结合单槽反电动势的特征谐波和绕组分布系数的推导结论,获得FSCW-PMSM局部失磁的单相反电动势的特征谐波理论求解方法。
在不同数量永磁体发生失磁故障时,对电机单相反电动势进行谐波分析,明确了单相反电动势各特征谐波的幅值随失磁永磁体数量增大呈周期性变化。

