电动汽车驱动用分数槽永磁同步电机电磁噪声优化
白学森
(厦门金龙联合汽车工业有限公司,福建 厦门 361023)
0 引 言
分数槽永磁同步电机因齿槽转矩低、转矩脉动小、恒功率运行区域的磁阻转矩占比高等优点被广泛用作新能源电动汽车的驱动电机[1-3]。但由于分数槽永磁同步电机中含有较低阶数的径向电磁力波,导致其电磁噪声水平高于一般的整数槽配合电机,因此研究阶次较低的径向电磁力波对抑制电机的电磁噪声至关重要[4-6]。
永磁同步电机的电磁噪声问题一直是电动汽车驱动电机技术领域的研究热点,其不仅关系到电机的性能,还会影响到整车的运行能力。电机的电磁噪声主要由定子齿部的径向电磁力引起,可通过优化定子齿槽结构来削弱定子齿部受到的径向电磁力,降低电磁噪声。文献[7]提出一种定子齿顶偏移的结构来削弱定子齿部受到的径向电磁力,并通过试验对比验证了该研究方法的正确性。文献[8]利用定子齿削角的方法对近极槽表贴式永磁同步电机的振动噪声进行了研究,有效降低了电磁噪声。文献[5]通过在定子齿上开辅助槽的方法改变电机的极槽配合来削弱对分数槽永磁同步电机空载电磁振动和噪声起主要作用的激振力波。文献[9]基于多目标遗传算法对电机的定转子冲片进行定向优化,分析了转矩脉动、输出转矩和齿槽转矩对电机振动噪声的影响。文献[10]通过多项式拟合的关键系数对结构参数进行敏感性分析、筛选和分级优化,以达到既抑制电机的振动噪声又不降低电机输出性能的目的。文献[11]利用粒子群多目标优化算法对经过向量拟合得到的永磁同步电机结构参数的回归方程进行寻优,实现电机效率和噪声的优化。
本文以一款电动汽车驱动用8极36槽内置式永磁同步电机为例,通过分析定子齿部受到的主要阶次径向电磁力波的特性,提出一种基于Pareto前沿对定子齿顶开辅助槽的齿槽参数多目标优化的方法。通过对定子齿顶辅助槽及齿槽参数的优化,找到所受径向电磁力最小的相对最优解,降低电机的电磁噪声。
1 电机有限元分析
1.1 电机二维有限元模型及主要性能参数
本文研究的电动汽车驱动用8极36槽内置式永磁同步电机的二维有限元模型如图1所示,电机的主要性能参数见表1。

图1 电机二维有限元模型

表1 电机主要性能参数
1.2 径向电磁力分析
电机的电磁噪声主要由作用于定子铁心内表面的径向电磁力使定子铁心振动变形引起的[12-13]。首先对电机定子齿部受到的径向电磁力进行分析,根据麦克斯韦张量法得到径向电磁力的解析表达式为

(1)
式中:pr为r阶径向电磁力波幅值;μ0为真空磁导率,μ0=4π×10-7H/m;Br为径向气隙磁密;Bt为切向气隙磁密,由于切向气隙磁密远小于径向气隙磁密,通常忽略不计。
电机的径向气隙磁密由气隙磁势和气隙磁导相乘得到,可由下式表示:
Br=fΛ=(fr+fs)Λ
(2)
式中:f为气隙磁势;fr为转子磁势;fs为定子磁势;Λ为气隙磁导。
电机在空载时,转子永磁体在气隙中产生的磁势为转子磁势;电机在负载时,转子磁势和三相绕组产生的定子磁势相加得到气隙磁势,可以表示为
fr=∑Fμcos(μωt-ωpθ)
(3)
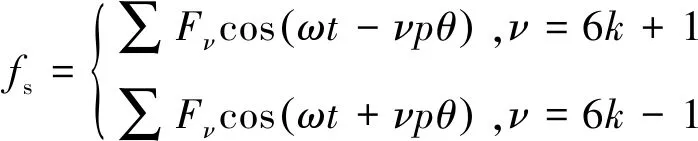
(4)
式中:Fμ为永磁体μ次谐波磁势的幅值,μ=1,3,5,…;ω为转子旋转的电角频率;p为永磁体的极对数;θ为圆周位置角;Fν为ν次谐波磁势的幅值;k为正整数。
不考虑转子偏心的影响,且假设转子表面光滑的情况下,气隙磁导由不变磁导和定子开槽引起的气隙磁导两部分组成,可表示为
Λ=Λ0+∑Λkcos(kZθ)
(5)
式中:Λ0为气隙的不变磁导;Λk为定子开槽引起的气隙磁导;Z为定子槽数。
电机的气隙磁导与定子槽数有关,通过增加定子槽数能够改善气隙磁导的分布。根据式(1)~式(6)得到径向电磁力的表达式为

(6)
式中:r为电磁力波阶数;ωr为r阶电磁力波的旋转角频率;pr为r阶径向电磁力波幅值;θ为圆周角位置;φr为相位角。
本文通过在定子齿顶开槽辅助槽的方法来改变电机的极槽配合,降低因定子开槽引起的齿谐波,并通过Optislang多目标优化平台对定子辅助槽和齿槽的结构参数进行多目标优化,找到对应电磁力波最小的一组相对最优解,以削弱较低阶次的电磁力波对电磁噪声的影响,从而达到降噪的目的。
对于8极36槽配合的永磁同步电机来说,电磁力波阶数与整数槽配合电机的基本相同,但由于分数槽配合,引入了阶次更低的4阶电磁力波,即电机的极对数p[12]。由于定子铁心动态形变的振幅近似与电磁力波阶次的4次方成反比,低阶次的电磁力波更容易引起较大的振动噪声,所以本文主要关注低阶次的电磁力波[5]。表2中列出了对电机优化前额定转速下空载和负载两种工况下的电磁力波时空分离得到的0阶和4阶主要的电磁力谐波分量,其中f1为电机额定转速时的机械转频。

表2 优化前8极36槽电机径向电磁力谐波分量 kN/m2
从表2可以看出,负载工况的电磁力密度幅值高于空载工况。对于空间阶次为0的电磁力波,72倍频时的电磁力密度幅值最大,其次是8倍频和24倍频;对于4阶次的电磁力波,32倍频时的电磁力密度幅值最大,且电机负载时的电磁力密度幅值为13.955 kN/m2,应该注意该谐波对电磁噪声带来的影响。
2 结构优化设计
2.1 定子辅助槽及齿槽参数
在满足电机主要性能参数的基础上,对定子齿上开辅助槽的齿槽参数进行优化,削弱径向电磁力的同时优化电机的输出转矩,以达到降低电磁噪声的目的,电机的定子辅助槽及齿槽的结构参数如图2所示。

图2 定子辅助槽及齿槽结构参数
在转子冲片结构确定的情况下,建立定子齿槽的参数化模型,并将不同运行工况下的有限元模型均设置成相同的优化参数,以实现定子冲片结构的完全统一,本文定子齿槽及齿顶的辅助槽的初始参数及其参数的范围如表3所示。

表3 电机定子齿槽初始值及优化参数范围 mm
本文的定子槽型选为平底槽,根据槽型结构合理选择优化参数的范围,以保证定子冲片的参数化模型不会出错。
2.2 Optislang多目标优化
将不同工况下的二维有限元模型设置好定子辅助槽、定子齿槽的优化参数和目标函数,然后通过确定性试验设计(DOE)的方法对优化参数进行敏感性分析,检测对径向电磁力影响较大的重要参数及目标函数间是否存在冲突,再进一步进行多目标优化;在满足优化参数范围、目标函数和约束条件的情况下获取相对最优解[14-15]。
大多数实际的优化问题包含多个设计变量和优化目标,将其转化为设计变量x=(x1,x2,…,xn)T与等式约束hk(x)和不等式约束gj(x)间的多目标优化问题。既满足变量范围又满足约束条件的可行解构成了n维设计空间,可以表示为
优化目标:
fm(x),m=1,2,…,M
(7)
约束及参数范围:

(8)

设计空间内的每个设计变量x,映射到M维目标空间均能得到一个点,该点对应一个解向量z=(z1,z2,…,zM)T。在目标准则互斥的情况下,并不存在唯一解,所以需要优化目标之间的妥协,以寻找最佳平衡解。如果一个解不被任何其他解所支配,则目标空间中的对应点为Pareto最优解,所有Pareto最优解构成Pareto前沿[10]。

图3 不同工况下优化目标的Pareto前沿
利用上述优化算法能够得到电机不同运行工况下的Pareto前沿,图3中的黑点为满足三个谐波含量约束的最优解,每个黑点对应一组设计变量值,通过权衡不同电机工况下的目标函数,电机定子齿槽及辅助槽优化后的参数见表4。

表4 电机定子齿槽优化后参数 mm
3 优化后性能分析
3.1 电磁力分析
电机优化前后4阶径向电磁力不同频率倍数下的电磁力密度对比,如图4所示。由图4可见,电机优化后的4阶径向电磁力波不同谐波频率下的径向电磁力密度均得到了削弱,尤其是32倍频的谐波幅值,从优化前的13.95 kN/m2降低到4.99 kN/m2,其次是40倍频,表明该方法能够有效削弱电磁力。

图4 4阶径向电磁力频谱分析
3.2 电机输出转矩分析

图5 优化前后电机转矩对比
电机优化前后,额定工况下的转矩输出对比如图5所示。由图5可见,优化后电机输出转矩的平均值为121.5 N·m,比优化前电机输出转矩的平均值小1.2 N·m,在满足电流限制内均满足电机的额定转矩要求。同时,电机的转矩脉动也得到了优化,降低了16.3%。
3.3 模态分析
利用有限元方法计算得到定子的低阶模态振型,如图6所示。电机在优化前后,二者定子各阶模态下的固有频率相差甚微,所以只列出了电机优化前的低阶模态振型及固有频率。当电磁力谐波的频率等于或者接近电机的固有频率时,电机将发生共振现象,使电机的振动噪声加剧,所以研究电机模态是为了考虑对应固有频率下电机是否会产生共振[16-18]。

图6 电机定子低阶模态振型
3.4 电磁噪声分析
本文8极36槽永磁同步电机采用转子V型分段斜极的方式来削弱齿谐波。将二维有限元模型计算得到的不同工况下的电磁力分别加载到对应的分段定子铁心上,如图7所示。利用模态叠加原理对谐响应进行分析,再将谐响应的计算结果导入到Harmonic Acoustics模块,对电磁噪声进行计算,得到电机优化前后的声场结果[19-20]。

图7 电机分析谐响应
图8为电机优化前后空载工况下的电磁噪声对比。其中,图8(a)为电机转速10 000 r/min时,不同谐波频率所对应电磁噪声的分布情况;图8(b)为电机不同转速下的32倍谐波频率所对应电磁噪声的分布情况。由图8可见,电机的声功率在极数的整数倍谐波频率附近出现波峰,且在转速10 000 r/min时,32倍频的声功率达到最大,优化前的最大声功率为102.7 dB,优化后的最大声功率为98.8 dB,减小了3.9 dB。在10 000 r/min转速下,32倍谐波频率为5 333.3 Hz,与电机4阶模态的固有频率相近,导致电机的振动噪声增大,所以在电机设计过程中要考虑共振对电磁振动噪声产生的影响,尽量避开共振频率点。

图8 电机优化前后电磁噪声对比
4 试验验证
为了验证仿真计算的准确性,对优化后的样机进行噪声试验,结果如图9所示。由图9可见,在整个电机的运行区间,32阶次电磁噪声最为明显,且随着转速的增加而变大,电机的转速范围在9 500~11 000 r/min时噪声问题最为突出,最大声功率为98.0 dB,与仿真结果相差较小。该结果与上述电磁力分析和模态分析相一致,电机转速在10 000 r/min附近时,32倍谐波频率与电机4阶模态的固有频率相接近,导致电磁噪声增大。

图9 样机试验测得的噪声瀑布图
5 结 语
本文以一台电动汽车驱动用8极36槽内置式永磁同步电机为例,提出一种基于Pareto前沿对定子齿顶辅助槽及齿槽参数的多目标优化方法,削弱定子齿部受到的径向电磁力引起定子铁心振动形变而产生的电磁噪声,对电机优化前后的电磁力、电磁转矩等方面进行了对比分析,并对优化后的样机进行了试验验证,得到以下结论:
(1) 8极36槽配合电机引入了阶次更低的电磁力,其对电磁噪声的影响更大,通过定子齿顶开辅助槽,改变电机的极槽配合,不仅削弱定子齿部受到的径向电磁力,而且降低了转矩脉动。
(2) 在高速工况下,32倍谐波频率与4阶模态的固有频率相接近,导致电机的电磁噪声加剧,与样机的试验验证结果相一致,所以在电机设计的过程中应尽量避开低阶模态的固有频率,以免发生共振。
(3) 通过对定子辅助槽及齿槽参数的多目标优化,电机优化后的电磁噪声较优化前降低了3.9 dB,对优化后的电机方案进行试验验证,实际值与仿真值贴近,证明了该优化方法的有效性。

