基于电流残差估计的五相永磁同步电机定子故障检测与分类*

张 凯, 时维国

(大连交通大学 自动化与电气工程学院，辽宁 大连 116028)

0 引 言

五相永磁同步电机(PMSM)相比于三相电机，具有更低的转矩脉动、更高的功率密度以及更强的容错能力[1]，在工业应用中越来越受欢迎。同时，在电机长期运行期间，其安全性与可靠性也是需要解决的紧要问题，尤其在船舶电力推进[2]、航空航天[3]、电动汽车[4]以及轨道交通[2]等工作条件要求较高的场合，如有故障发生，轻则造成停机停产，重则危及生命安全。

五相PMSM约有37%的故障发生在定子[5]，定子故障又以匝间短路 (ITSC)故障和高电阻连接(HRC)故障居多，并且这两种故障具有相同的故障特征，很难区分。ITSC故障主要是由于电气应力、机械应力和过载导致定子线圈的匝间绝缘劣化引起的，若不能及时处理，相邻匝间的故障会迅速扩散到整个绕组，导致主绕组短路[6]。而HRC故障是一种渐进式故障，引起电机局部过热，对电机本身的损坏有限，HRC故障特征为相电阻增大而相电感不变。大多数情况下，只会恶化机器的运行性能，如增加转矩脉动、降低运行效率[7]。

目前，针对PMSM定子故障在线诊断已经开展了大量研究，主要方法有解析模型法、信号处理法和智能算法。基于解析模型的方法主要采用观测器估计或状态估计进行故障识别。文献[8]根据ITSC故障会对模型预测控制系统中价值函数产生影响，将价值函数的直流分量和二次谐波分量存储到表格中，利用查表的方式诊断ITSC故障。文献[9]根据ITSC数学模型建立故障观测器，估计故障情况下电流异常变化，进行故障诊断。基于信号处理的方法主要选择电机电流、电压进行频谱分析提取故障特征量。文献[10]利用改进小波包变换提取ITSC故障电流信号，对早期ITSC故障进行分析和检测。文献[11]采用信号注入的方法，利用定子电流直流分量的增量，对HRC故障的严重程度和故障相位进行检测。文献[12]分析了零序电压的幅值与初始相位，提出了基于改进带相角差的故障指示器，用于HRC故障检测与故障相识别。利用智能算法进行故障诊断，需要大量的数据训练故障诊断模型。文献[13]考虑时间序列数据对时间的依赖性，利用长短时记忆构造编码器和解码器，提出基于递归神经网络的ITSC故障程度估计方法。文献[14]基于条件生成式双对抗自编码网络生成大量数据样本，然后利用卷积神经网络提取特征对ITSC故障进行诊断。

上述故障诊断方法只是检测单一故障，电机运行过程中ITSC故障与HRC故障都会引起电机不对称性，具有相同故障特征。文献[15]采用注入高频方波信号的方法，利用ITSC故障和HRC故障高频阻抗的差异，检测三相电流均方根值比率的异常变化，区分两种故障。文献[16]利用零序电压分量检测电机异常状态，然后根据ITSC故障时零序电压高频分量幅值与注入信号频率成正比，而HRC故障时零序电压高频分量幅值恒定，进行两种故障类型识别。

本文提出了一种基于电流残差估计的定子故障诊断方法，根据高频时电感与电阻的阻抗特性不同，进行ITSC故障和HRC故障的分类研究。首先根据五相PMSM正常运行与发生两种故障时电流不同，采用观测器估计电流的故障残差，在线检测电机的异常状态。在检测到电机异常运行时，向电机驱动系统注入高频电流信号，利用高频分量来识别故障类型。然后对两种故障的故障程度与故障相位进行研究，分析转速和负载变化对故障程度的影响。最后，通过仿真验证证明本文提出的电机定子故障检测与分类方法的有效性。

1 五相PMSM故障模型

1.1 ITSC故障模型

假设ITSC故障发生在A相，故障模型如图1所示。其中Rf是匝间绝缘劣化的短路电阻，if是短路绕组内的故障循环电流。利用ITSC故障的等效电路图进行故障研究，如图2所示。电机每一相均有相电阻、自感、互感、反电动势，相绕组分为健康部分和短路部分。短路匝数比μ为短路匝数与总匝数之比。

图1 ITSC故障发生在A相的故障模型

图2 A相ITSC故障等效电路图

基于等效电路，A相ITSC故障忽略互感的电压平衡方程为

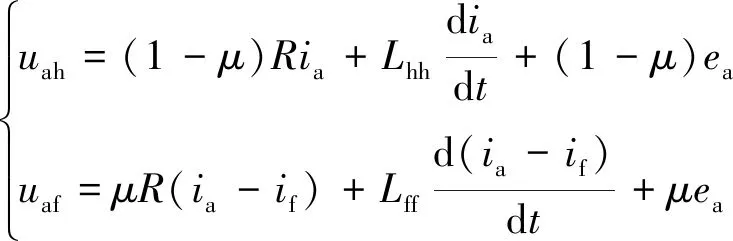
(1)

式中：uah和uaf分别为健康部分和故障部分绕组电压，无故障发生时uaf=0；Lhh和Lff是正常绕组自感和短路绕组自感，与定子绕组自感L的关系为Lhh=(1-μ)2L，Lff=μ2L；R为定子电阻；ea为定子反电动势；ia为定子电流。

由于A相多了故障部分电压方程，电机模型维数增加至六维。通过坐标变换，得到旋转坐标系下的电机A相定子绕组发生ITSC故障时的电压平衡方程。由于五相PMSM发生ITSC故障时d1-q1轴电流故障特征明显，所以在d1-q1轴下进行研究，交直轴电压方程表示为

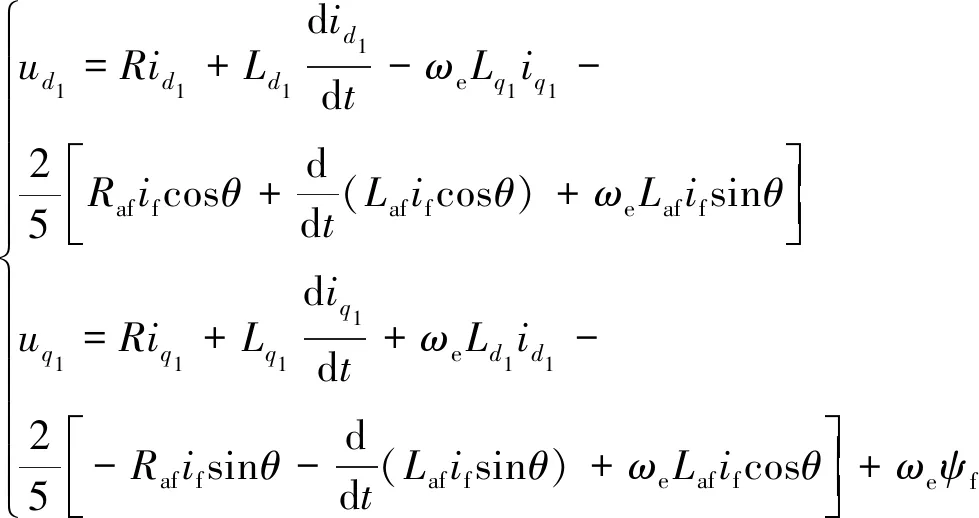
(2)

式中：d1轴电压、电流、电感、反电动势分别为ud1、id1、Ld1、ed1，q1轴类似；θ是电机转子电角度；ωe是电角速度；本文采用隐极式电机分析，Ld1=Lq1=L，Laf=μL；Raf=μR；ψf为永磁体磁链。

1.2 HRC故障模型

电机发生HRC故障时，故障模型可以用电机相绕组连接附加电组Rdd来表示，如图3所示。假设HRC故障发生在A相绕组，其他四相正常，A相电压方程可表示为

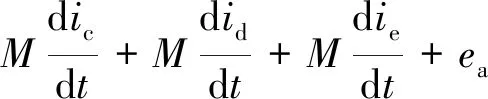
(3)

式中：M为定子绕组互感。

d1-q1轴的电压方程为

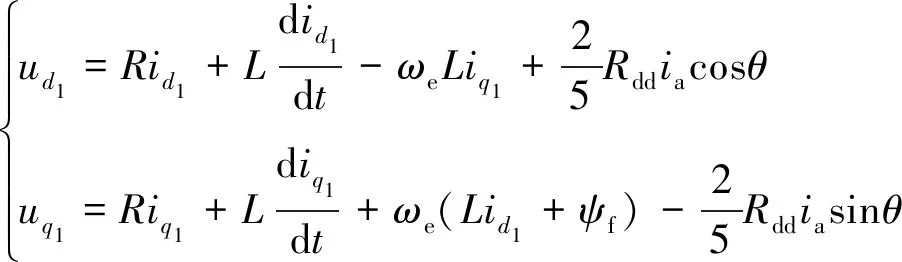
(4)

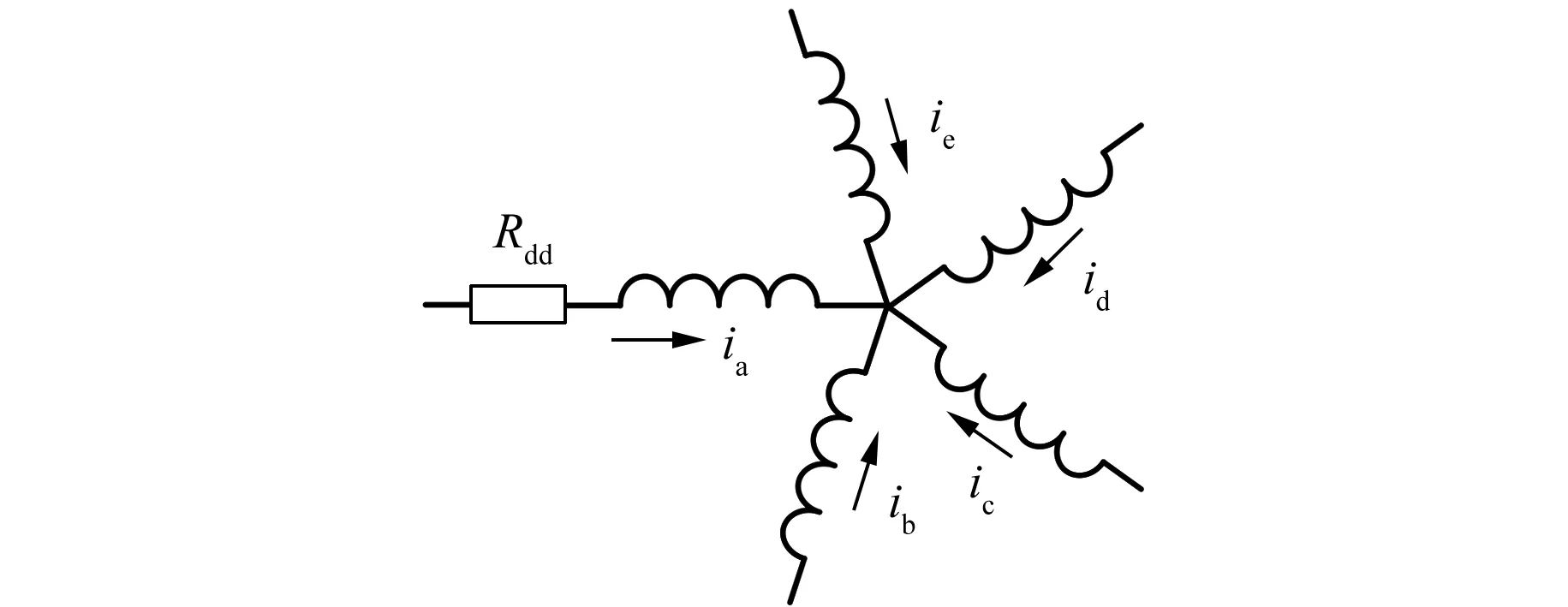
图3 HRC故障模型

2 故障研究

2.1 电流估计

五相PMSM正常运行时d1-q1轴电压平衡方程式为

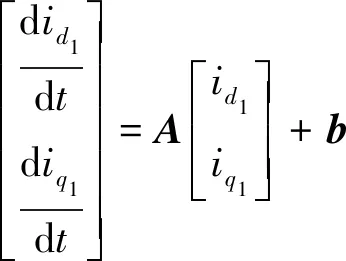
(5)

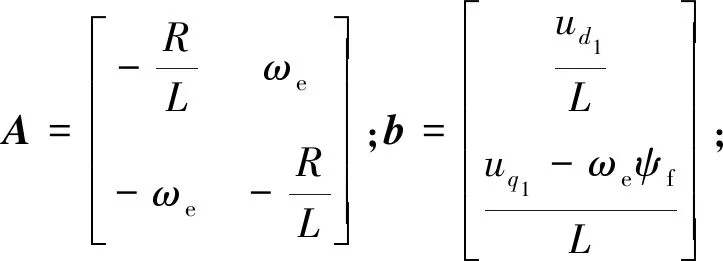
矩阵函数式(6)的通解可以写为

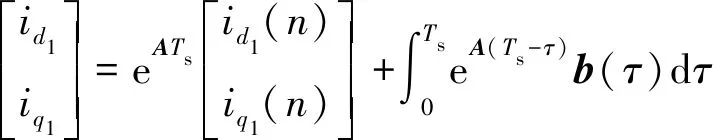
(6)

式中：Ts为采样时间；id1(n)、iq1(n)为n时刻电流值；τ为时间变量。

由于观测器用于观测稳态时的电流[17]，可以忽略式(6)的导数分量，稳态时电流方程为

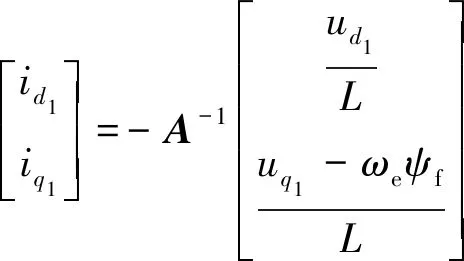
(7)

结合式(6)和式(7)，得到电流的估计值id1(n+1)、iq1(n+1)为

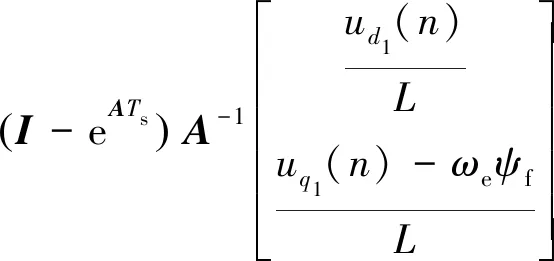
(8)

式中：I为二阶单位矩阵。

式(8)中矩阵A的两个特征值实部为负数，这表示eATs会随着时间的推移而迅速减小，电流估计值接近稳态时的电机电流值。

2.2 故障电流估计

当电机发生ITSC故障和HRC故障时，估计电流方程中多了故障特征电流idf和iqf，含有故障电流的电流稳态方程为

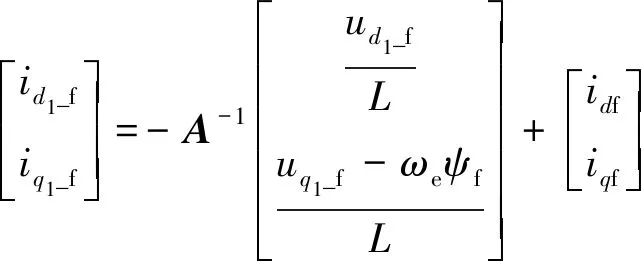
(9)

电机发生ITSC故障时，根据式(2)，并代入故障循环电流if=Ifsin(θ+φ)(If和φ为故障循环电流幅值和初相位)，得到故障电流idf_ITSC与iqf_ITSC为

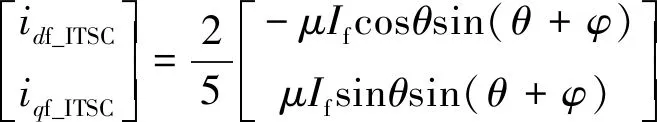
(10)

电机含有ITSC故障时，d1-q1轴多出了含有故障特征的电流项idf_ITSC与iqf_ITSC。电机正常运行时，电流估计值不含二次谐波分量。当发生ITSC故障后，电流估计值发生变化，估计电流中含有幅值为2μIf/5的二次谐波分量，其初相位与故障电流if的初相位有关。并且估计电流二次谐波的大小与μ和故障电流幅值If有关。

电机发生HRC故障时，根据式(4)，并带入相电流ia=Iasinθ，得到含有HRC故障特征的电流项idf_HRC与iqf_HRC为

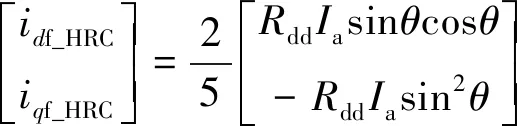
(11)

从式(11)可以看出，发生HRC故障时，d1-q1轴估计电流多出了幅值为2RddIa/5的二次谐波分量。

分析式(10)和式(11)可知，ITSC和HRC故障电流估计残差都含有二次谐波，可以根据电流残差判断电机是否发生故障，但是仅凭借电流残差的二次谐波不能区分两种故障。

2.3 故障分类

比较图1和图3，可以看出ITSC故障会改变电机相电阻和相电感，HRC故障只改变电机相电阻。因此，可以根据高频时电感是否占主导地位，区分两种故障。根据文献[18]，逆变器最佳开关频率为20 kHz，为了减少逆变器开关的影响，注入信号选择1 kHz左右的高频信号。高频注入信号如式(12)所示，高频注入电流的幅值为Ih，高频电流的角频率为ωh。在高频条件下，由于ωe远小于ωh，电阻压降和反电动势可以忽略[18]，d1-q1轴电压方程如式(13)所示。

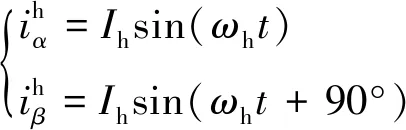
(12)

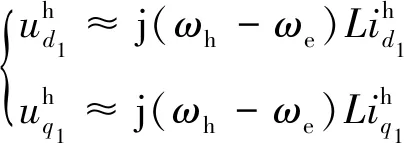
(13)

式中：j(ωh-ωe)L为高频条件下的电机阻抗；j为虚数单位。

当A相发生ITSC故障时，故障电流包含高频分量，高频条件下电压方程为

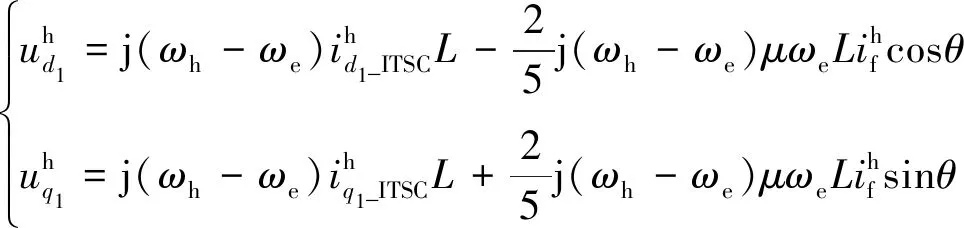
(14)

联立式(13)和式(14)，得到故障时高频电流表达式：

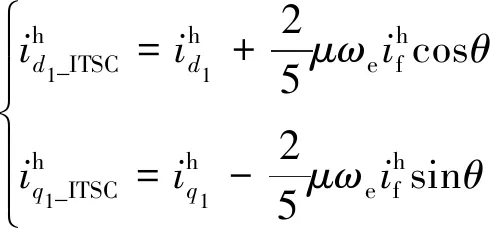
(15)

同理可得HRC故障时高频电流表达式：

(16)

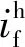
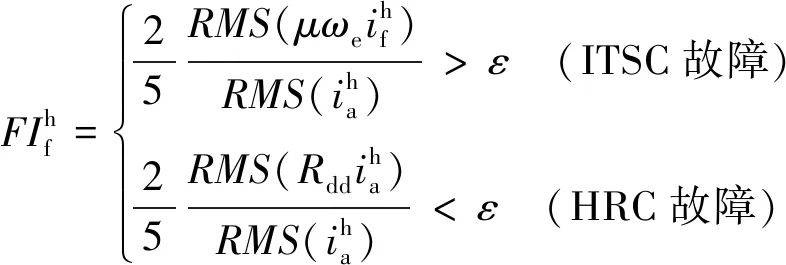
(17)

3 故障诊断

基于观测器的电机故障检测系统，其核心是一个非线性状态观测器。本文利用Kalman滤波器估计故障残差。系统状态空间表达式为

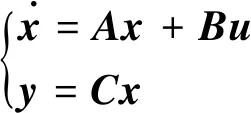
(18)

故障电流检测观测器表达式为

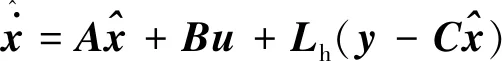
(19)

式中：上标“＾”表示变量的估计值；Lh为滤波器的增益。

残差r可以定义为

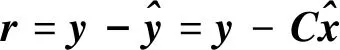
(20)

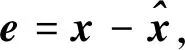
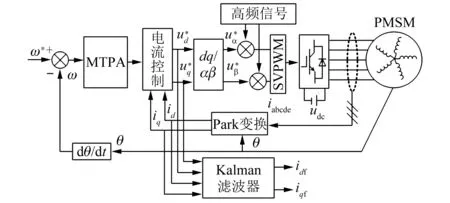
图4 故障残差估计

3.1 故障诊断策略

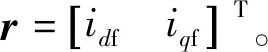
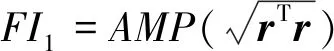
(21)

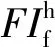
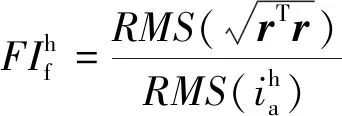
(22)

3.2 ITSC故障程度与故障相位分析

3.2.1 故障程度

根据式(10)和式(21)，当电机发生ITSC故障时，故障程度FI1为

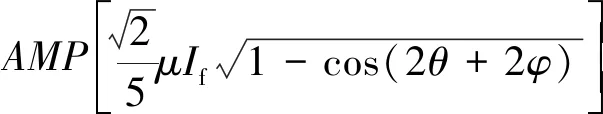
(23)

由式(23)可知，μ为短路匝数比，不受电机负载和转速变化的影响，而If受电机转速变化的影响。仅仅以FI1作为检测ITSC故障程度的指标，故障程度对故障敏感度降低。文献[21]指出，ITSC故障电流if与转速成正比。为了提高故障程度FI1的鲁棒性，检测ITSC故障时FI1_ITSC为

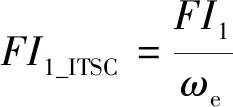
(24)

3.2.2 故障相定位

故障相位与故障循环电流if的初相位有关，但是故障循环电流是无法观测的。因此根据故障电流残差r计算故障相位：

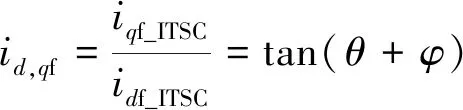
(25)

式中：θ=ωet。

根据文献[22]，故障循环电流if的初相位与故障相电流的初相位相等。假设一个周期内id,qf幅值达到最大值所对应时间为tφ，定子电流达到最大值所对应时间为tp，故障相标志位dj为tφ和tp时刻的角度差：

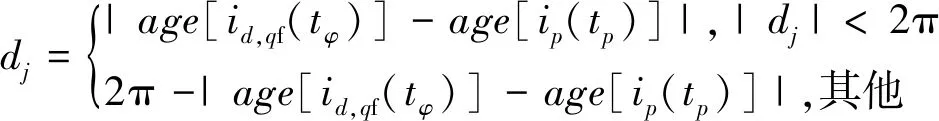
(26)

式中：age[id,qf(tφ)]为id,qf幅值达到最大时所对应的角度；age[ip(tp)]为ip幅值达到最大时所对应的角度；j=a,b,c,d,e;p=a,b,c,d,e。

表1列出每相故障时的dj理论值。故障相的dj为零，非故障相dj不为零。因此可以用dj定位故障的相位。

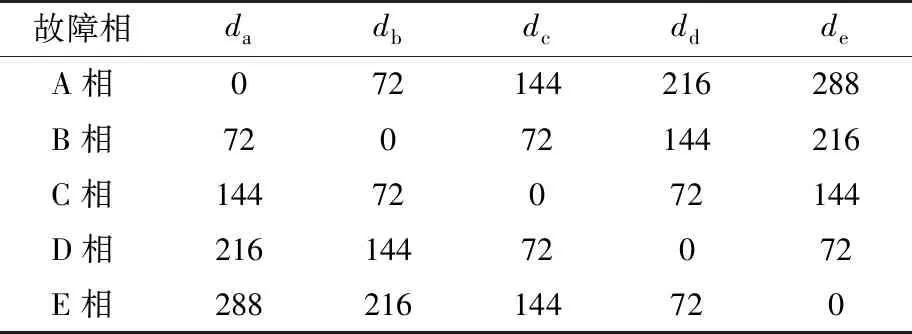
表1 故障相标志位 (°)

3.3 HRC故障程度与故障相位分析

3.3.1 故障程度

根据式(11)和式(21)，当电机发生HRC故障时，故障程度FI1为

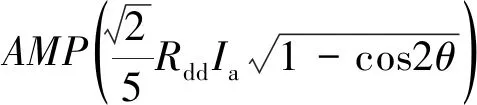
(27)

由式(27)可知，HRC故障程度与不平衡电阻Rdd和故障相电流幅值Ia有关，Ia受电机负载变化的影响。为了提高故障程度FI1的鲁棒性，检测HRC故障时FI1_HRC为

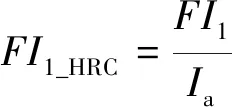
(28)

3.3.2 故障相定位

根据式(11)，HRC故障相位可以由iqf_HRC/idf_HRC计算得到，与ITSC故障类似，因此可以与ITSC故障使用相同的故障相定位方法。

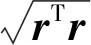
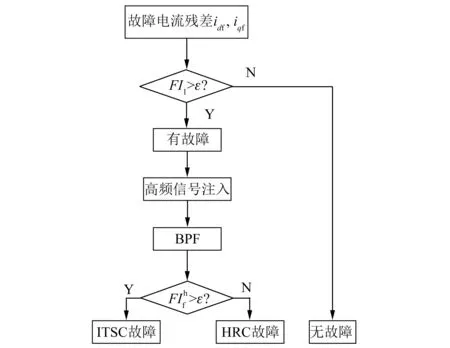
图5 故障诊断流程

4 仿真分析

为了验证提出的ITSC故障和HRC故障诊断方法的有效性，在MATLAB/Simulink下搭建故障诊断模型进行仿真验证。电机主要参数如表2所示。

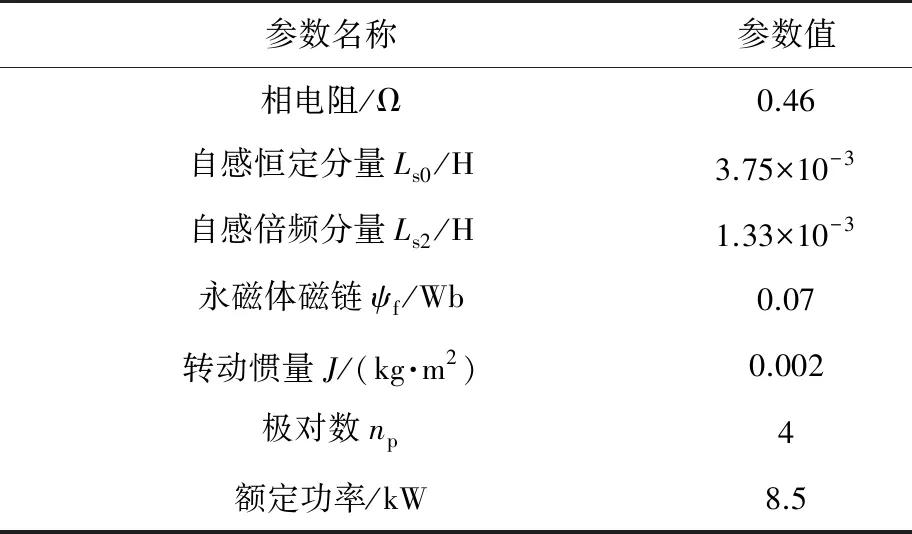
表2 电机主要参数

4.1 故障类别仿真分析

仿真研究分为两个时间段，在t=1 s之前，电机处于健康状态；t=1 s时，电机分别发生ITSC故障和HRC故障。电机转速为750 r/min，负载为5 N·m。ITSC故障发生在A相，μ=0.2，Rf=0.3 Ω；HRC故障发生在B相，Rdd=0.5 Ω。由图6可知，两种故障时，相电流特征不同，ITSC故障由于故障循环电流的影响，故障相电流幅值变大，非故障相电流幅值小幅变大。HRC由于故障相多了附加电阻Rdd，在端电压保持不变的情况下，故障相电流降低，非故障相电流没有变化。

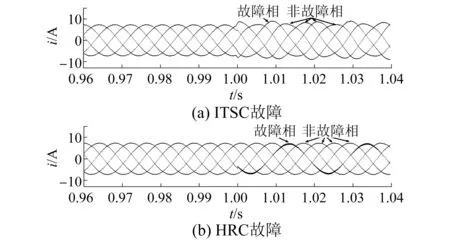
图6 定子电流

由图7可知，发生ITSC故障和HRC故障时，电机转速和负载转矩发生了波动，这两种故障都能引起电机振荡，降低电机运行效率。图8为d1-q1轴电流残差，发生故障时出现了波动。电机在基频50 Hz下运行，根据快速傅里叶变换(FFT)分析，故障时的电流波动频率为二次谐波，如图9所示。

图7 转速和转矩

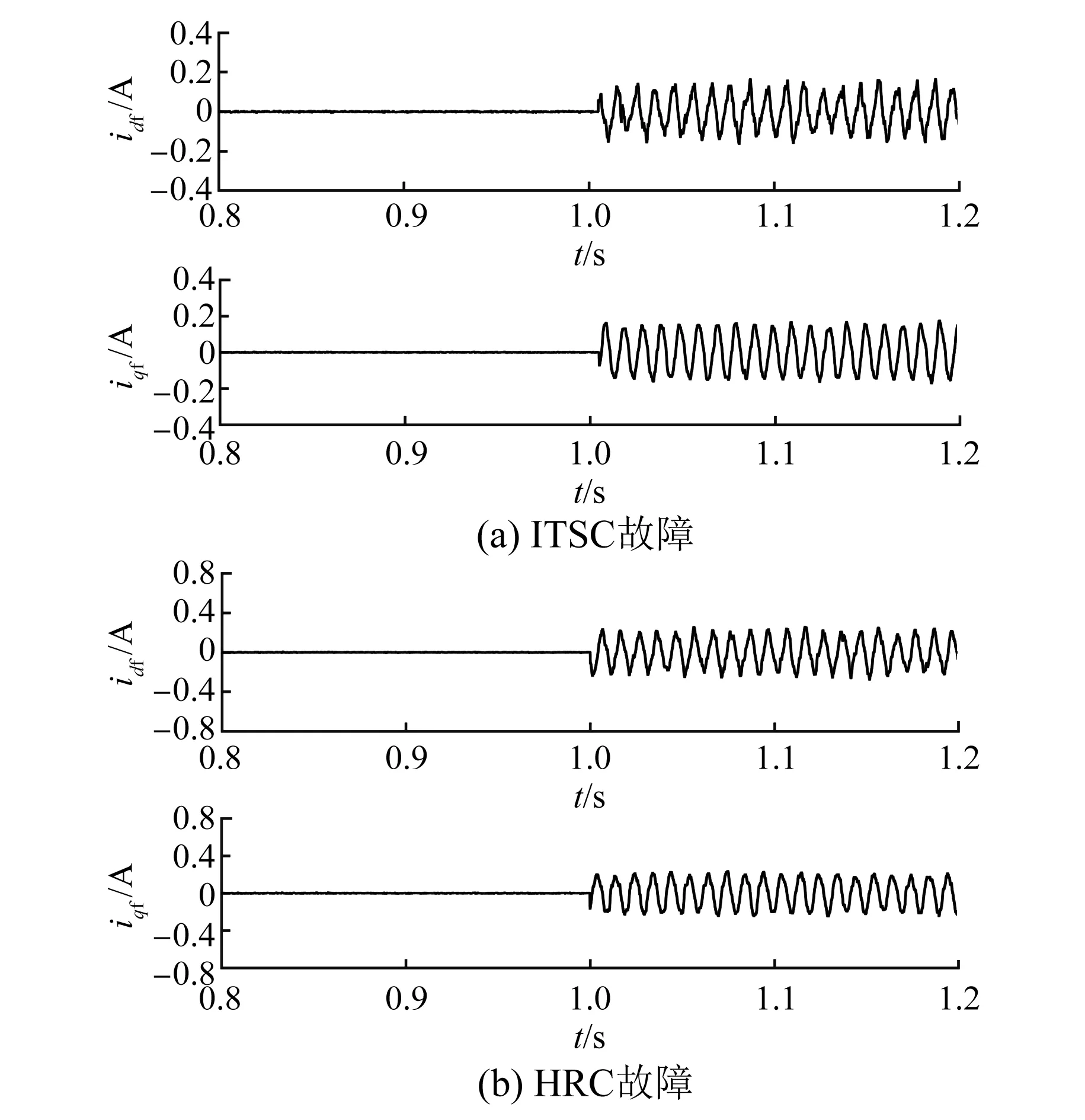
图8 故障残差idf和iqf

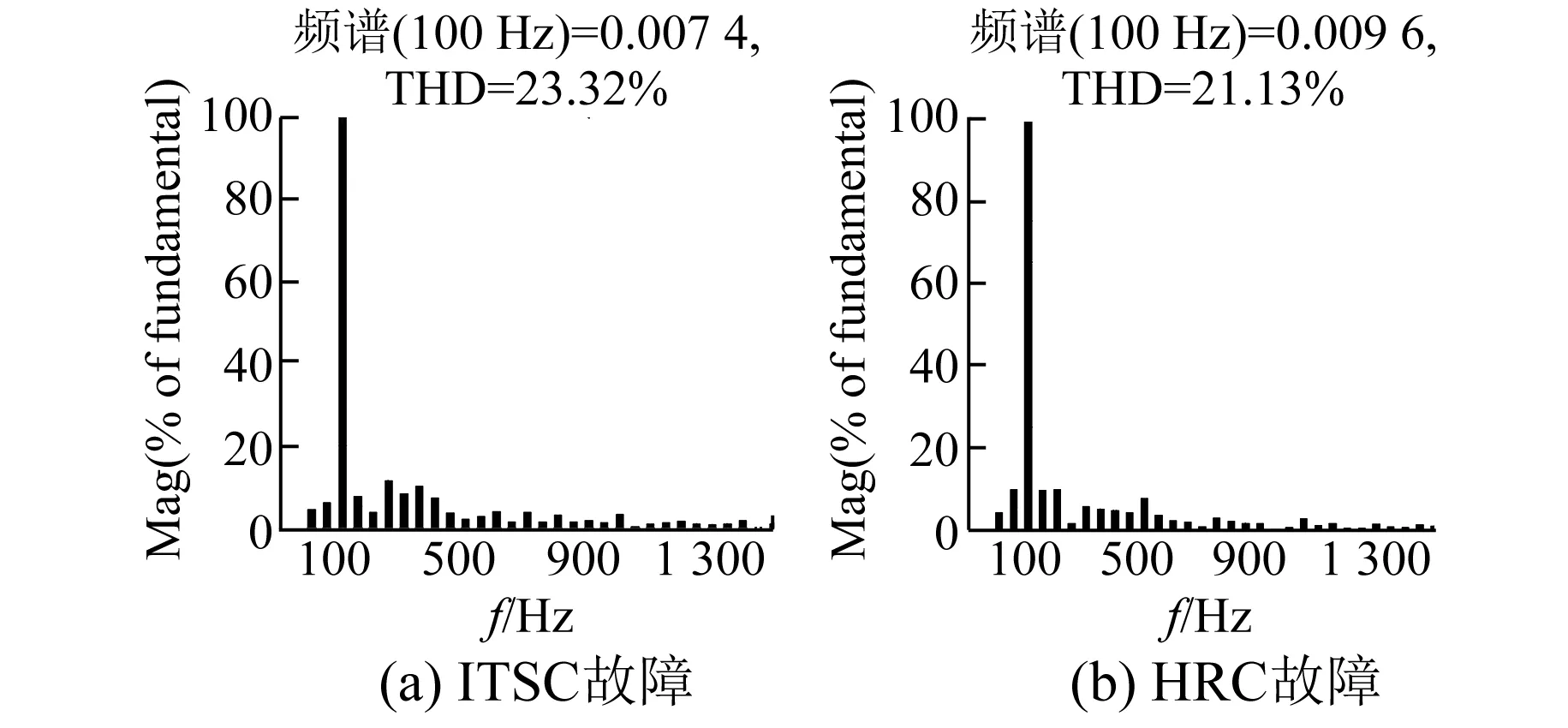
图9 故障残差FFT分析

图波形

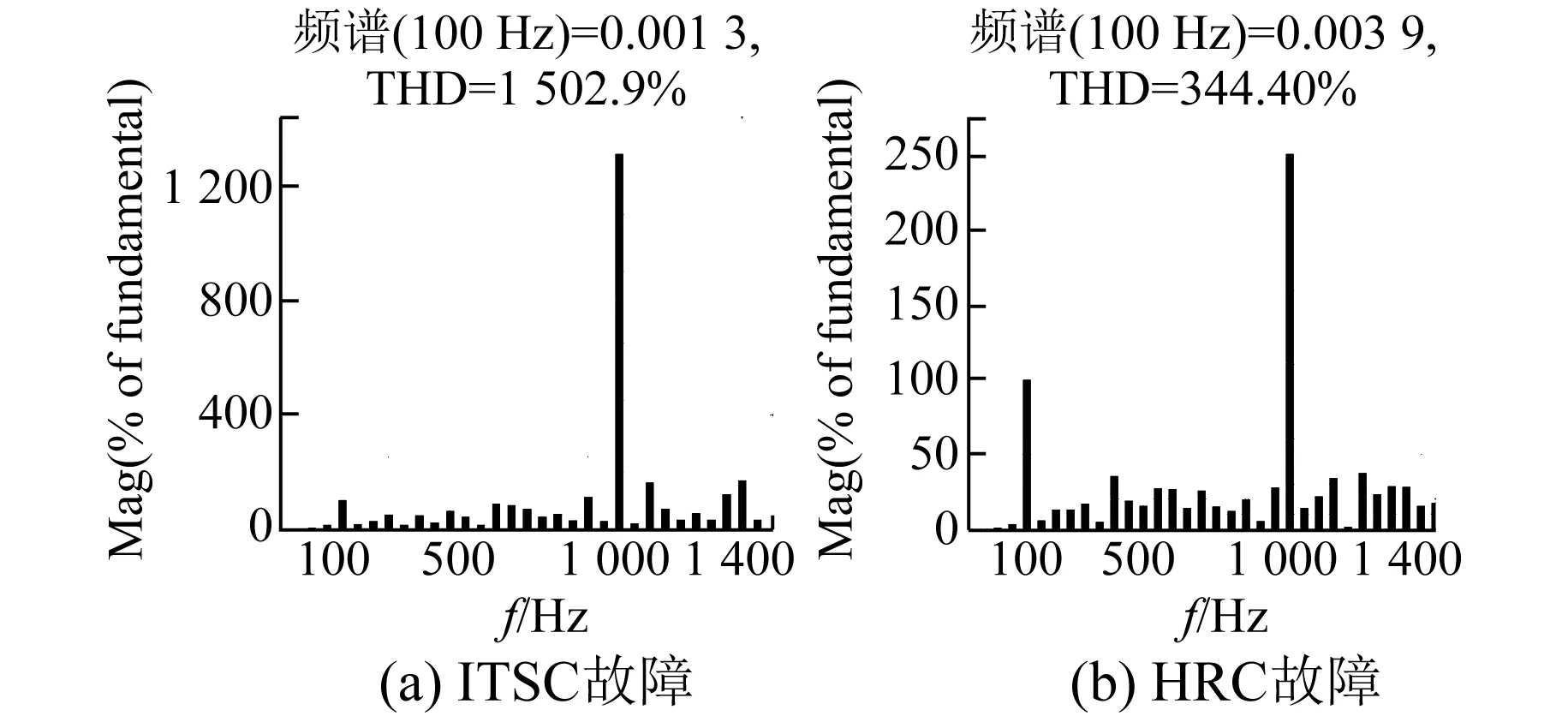
图11 高频FFT分析

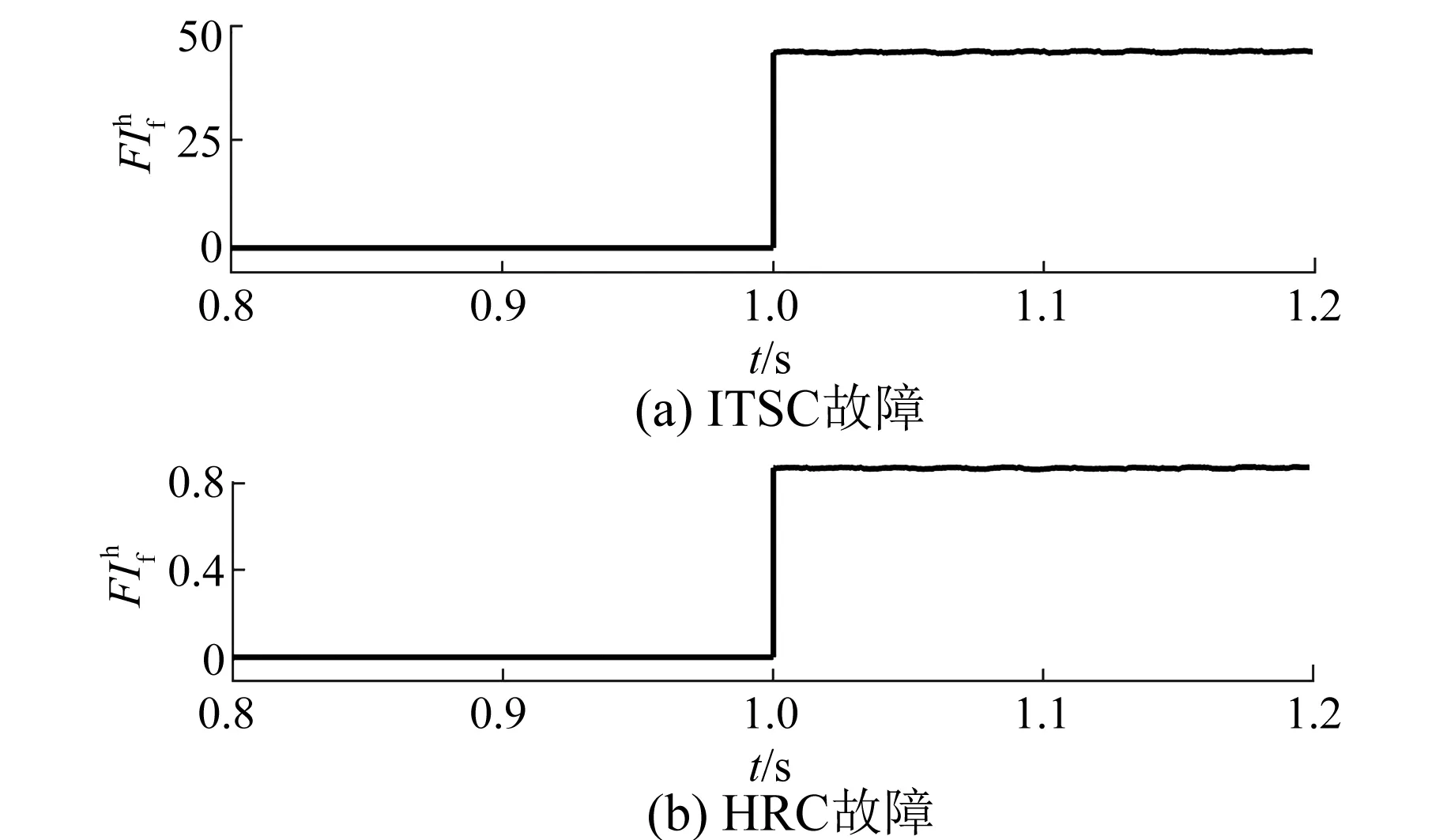
图波形

4.2 故障程度及故障相标志位仿真分析

ITSC故障程度FI1及故障相dj仍然以A相故障为例进行分析。为了分析ITSC故障不同故障程度时故障指标FI1和故障相标志位dj的值，需要对故障参数Rf和μ分别进行分析。图13为故障电阻Rf=0.3 Ω，短路匝数比μ不同时FI1和dj的值。可以看出，随着μ的增大，故障程度FI1增大；故障相标志位dj基本不变。图14为短路匝数比μ=0.2，短路电阻Rf不同时FI1和dj的值。随着短路电阻的增大，故障程度FI1变小，但是故障相标志位dj基本不随Rf变化而变化。由以上分析可知，FI1可以反映故障程度，并且根据故障相dj=0，非故障相dj≠0，能够判断故障相位。

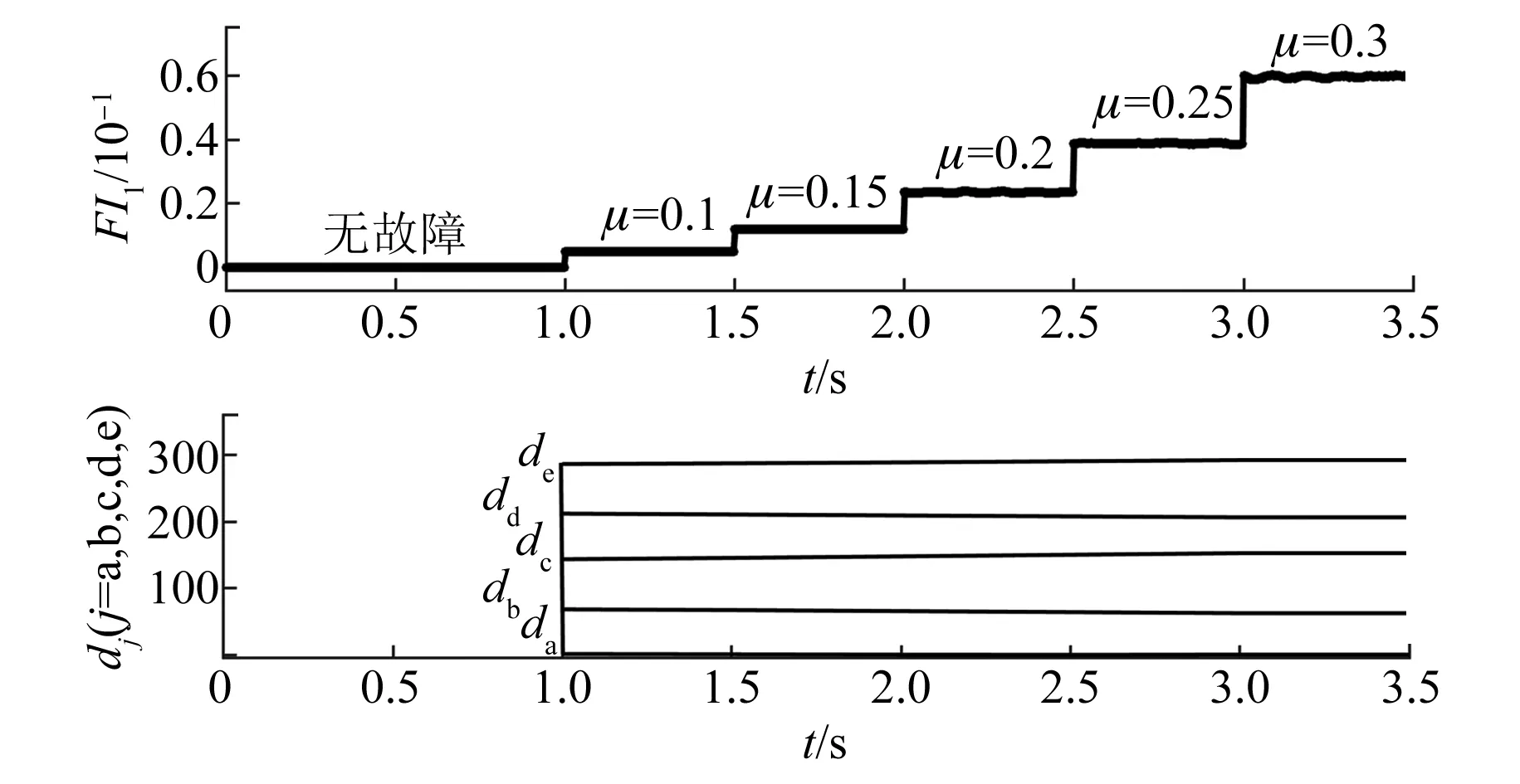
图13 Rf=0.3时故障程度与故障相位

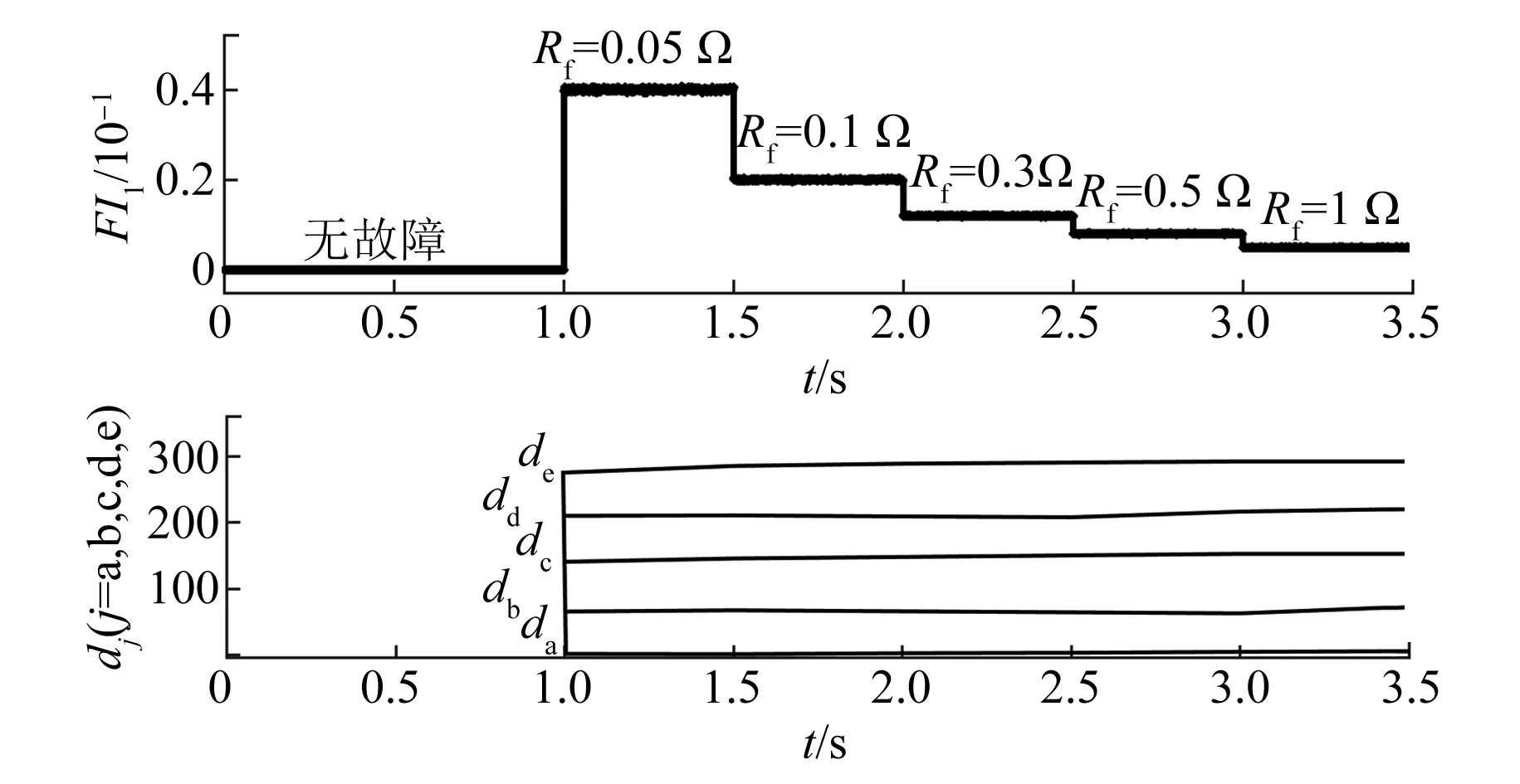
图14 μ=0.2时故障程度与故障相位

HRC故障程度FI1及故障相dj以B相故障为例进行分析。图15为附加电阻Rdd不同时，故障程度FI1和故障相标志位dj的值，FI1随着附加电阻Rdd的增大而增大，而dj不受Rdd的影响，B相dj=0，非故障相不为零。

4.3 故障程度鲁棒性仿真分析

图16为ITSC故障不同转速时FI1仿真分析，给出电机在300、750、1 000、1 500 r/min四种转速下的故障程度。可以看出虽然在同一转速下故障程度FI1随着μ增大而增大、随着Rf的增大而减小，但是转速变化时FI1与故障程度并不是一一对应的关系，即故障程度FI1在转速变化的情况下不具有鲁棒性。根据故障程度与转速的关系，改进故障程度FI1_ITSC为FI1与转速的比值。由图17可以看出，故障程度不再受转速变化的影响，只与μ和Rf有关。

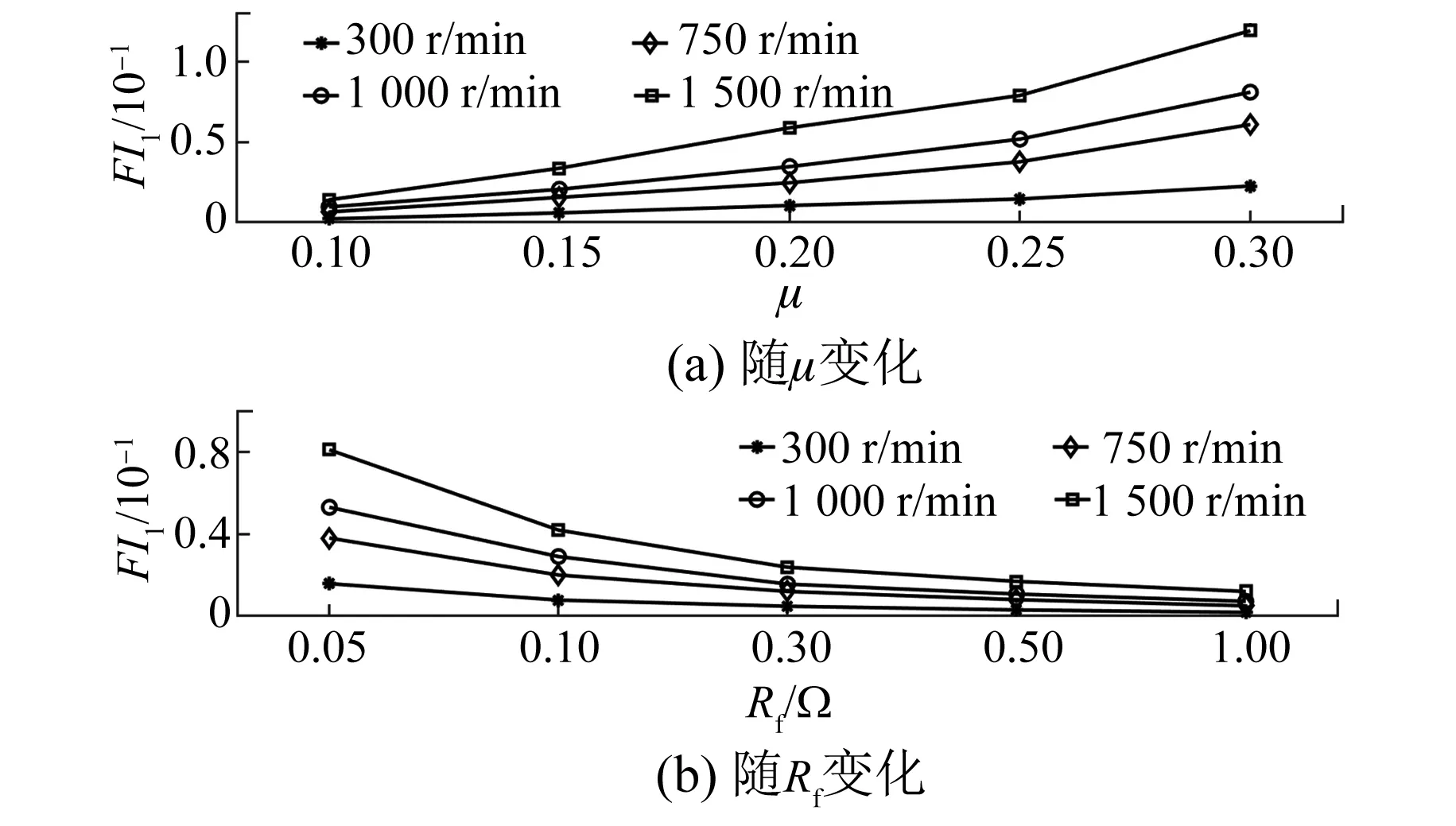
图16 不同转速时故障程度FI1

图17 不同转速时故障程度FI1_ITSC

电机负载变化会影响HRC故障程度的鲁棒性。图18为不同负载时故障程度FI1与FI1_HRC仿真分析，负载变化为1、3、5、10 N·m。可以看出FI1受负载变化的影响，而改进的故障程度FI1_HRC只随Rdd变化而变化，因此FI1_HRC对负载变化具有鲁棒性。

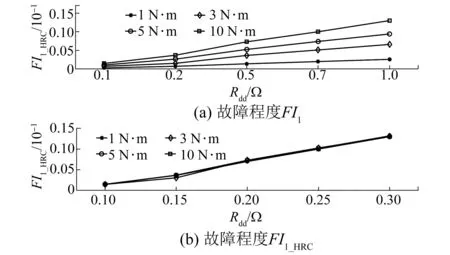
图18 HRC故障不同负载时故障程度

5 结 语

针对五相永磁同步电机定子匝间短路故障和高电阻连接故障，本文通过电流残差估计来检测电机故障状态，然后根据高频时电流差异区分两种故障，最后对故障程度鲁棒性进行分析。通过仿真验证了所提出方法的有效性，并得到以下结论：

(1) 该方法能够准确检测和识别五相永磁同步电机匝间短路故障和高电阻连接故障，并且能够定位故障相。

(2) 两种故障严重程度不受电机转速和负载变化的显著影响，具有较好的鲁棒性。

(3) 该方法不需要增加额外的设备和测量装置，不需要提取、采集新的信号。