基于NSGA-Ⅱ的局部范围搜索算法的电机参数优化*
黄朝志, 耿永民, 原红卫
(江西理工大学 电气工程与自动化学院,江西 赣州 341000)
0 引 言
在日常生活中多目标优化问题随处可见,人们往往希望在有限的资源中挑选出最优解,但实际情况往往是多个最优解共同存在,最优解的目标函数之间相互制约,使最优参数难以通过比较得出。因此人们往往通过制定一些技术指标来限定目标函数的范围以降低选择的难度[1]。转矩脉动、效率和平均转矩均可以作为目标函数,其中以效率为目标函数是为了更好地了解损耗的变化。为了观察局部的转矩脉动和平均转矩之间的约束关系,设置局部范围,使最优解集在该区域内产生,这对优化算法的搜索能力提出了更高的要求,算法必须拥有足够强的搜索能力才能得到最优解集。
非支配排序遗传算法(NSGA-Ⅱ)是由Deb等[2]提出的一种通用的多目标优化算法,在多目标优化问题中有着广泛的应用[3-5]。陈吉清等[6]使用NSGA-Ⅱ对开关磁阻电机样机的结构参数进行多目标寻优,优化的结果表明该方法能够有效地抑制转矩脉动。由于该NSGA-Ⅱ是Isight软件自带的算法,因此其结果还可以进一步优化。刁凯凯等[7]利用分层优化的方式进行多目标优化,通过对比分析确定可以获得最优的电磁性能,然而其有着鲁棒性差且容易受到加工误差影响的缺点。
NSGA-Ⅱ的优点是搜索的范围广,然而在全局搜索中牺牲了局部范围中的优秀解。为了解决传统NSGA-Ⅱ存在的问题,路艳雪等[8]提出改进的正态分布交叉算子和自适应调整变异方式,使Pareto最优面更加均匀连续地分布,但其自适应变异方式不利于搜索到更优解。栗三一等[9]提出了一种基于密度的局部搜索NSGA-Ⅱ算法,对稀疏的个体进行极限优化和随机搜索,使搜索能力和收敛速度得到提高,但是算法的计算量有一定的增加,使收敛速度减慢了。
本文提出基于NSGA-Ⅱ的局部范围搜索算法(RLS-NSGA-Ⅱ)。RLS-NSGA-Ⅱ相比NSGA-Ⅱ增强了局部搜索能力,同时为应对计算量的问题,RLS-NSGA-Ⅱ在局部范围内进行搜索,减少了搜索能力强导致的计算资源浪费。本文在算法优化的基础上将RLS-NSGA-Ⅱ应用于一种永磁辅助开关磁阻电机(该种电机通过在定子槽中嵌入永磁体,使其具有更好的电磁性能)的参数优化中,并加入有效单位保留策略,试验证明RLS-NSGA-Ⅱ在搜索能力和收敛性方面都明显优于NSGA-Ⅱ,并且最优解的参数更加符合实际需求。
1 电机拓扑结构和优化模型建立
1.1 电机拓扑结构
本文提出一种在外转子开关磁阻电机中加入永磁体的新型6/20混合励磁三相外转子永磁辅助开关磁阻电机,其结构如图1所示。该电机定转子由硅钢片叠压而成,定子分为六个分段定子,每个分段由两个辅助齿和一个Y型齿组成。一相的磁通路径如图2所示,永磁体就嵌入在辅助齿与Y型齿之间的槽口中,其中永磁体的磁性在分段定子中相反,在相邻的定子中磁性相对。定子极上有集中绕组,相对的两个绕组串联构成一相。外转子有20个极,本文在每个转子极上增加一个极靴角,以探究对电机运行参数的影响,极靴示意图如图3所示。混合励磁结构中的永磁体对开关磁阻电机磁场有增强的作用,进而改善电机的运行转矩。该电机的初始设计尺寸如表1所示。

图1 永磁辅助开关磁阻电机三维结构

图2 一相的磁通路径

图3 极靴示意图
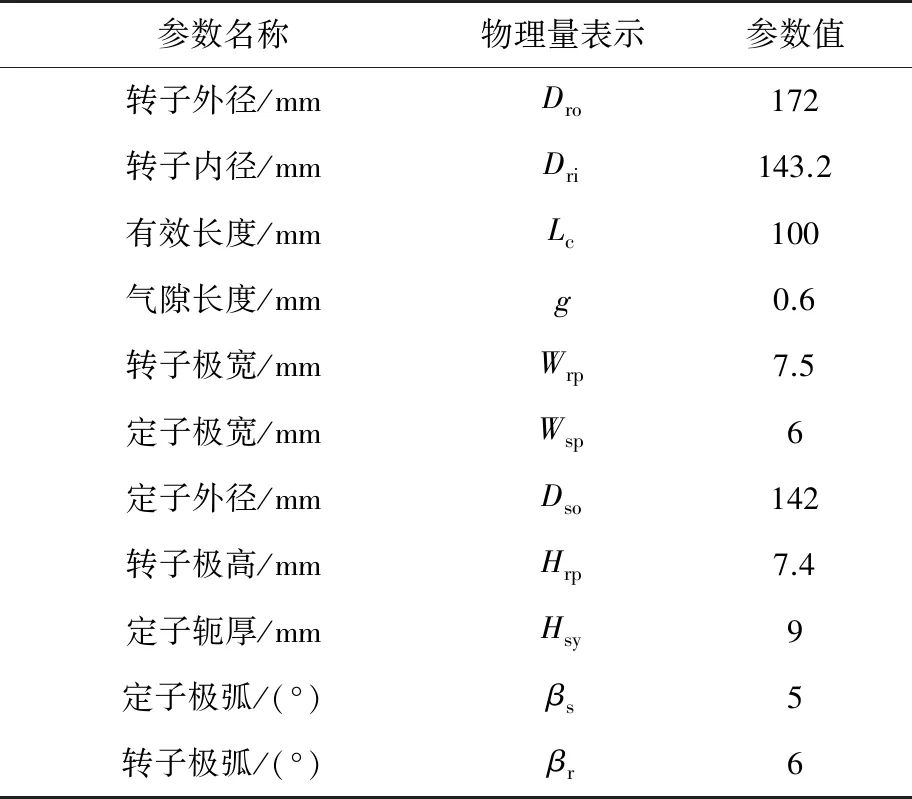
表1 初始设计尺寸
1.2 建立优化模型
本文将转矩脉动作为一个目标函数;在降低转矩脉动的同时,平均转矩的大小也是一个值得考虑的问题,因此将平均转矩也作为一个目标函数;最后将电机的运行效率作为一个目标函数。综上,本文选取的三个目标函数分别为转矩脉动、平均转矩和效率[10-11]。
本文选取5个结构参数和4个控制参数作为设计变量,对其进行皮尔逊相关系数分析,设计变量表和皮尔逊相关系数分布如表2和图4所示。

表2 设计变量表

图4 皮尔逊相关系数分布
由皮尔逊相关系数分布可以看出,匝数、极靴角、导通角、关断角和斩波电流等五个设计变量对三个目标函数的影响最大,因此选取此五个变量作为本优化的决策变量。利用响应面法对决策变量定义域内的样本点进行试验设计[12-14],样本点数据由Maxwell有限元软件仿真得到。本试验设计采用所需样本点少的Box-Behnken方法,样本点共有46个,使用Design-Expert软件对试验数据进行回归拟合分析,得到三个目标函数的二阶响应面方程。
1.3 保留有效单位
传统NSGA-Ⅱ的决策变量的数值是由随机数、交叉算子和变异算子决定的,在优化的过程中决策变量的优化会越来越精细,这导致在最后的优化结果中存在决策变量精度过高的问题。因此,针对永磁辅助开关磁阻电机的运行参数特点,对其优化参数进行有效单位保留。具体做法是:匝数进行取整操作,电流、开通角、关断角和极靴角保留小数点后一位。经过有效单位保留后,考虑到所有可能存在的解集,总个体数约4×107个。其中最小单位优化变异的最小单位的精度和有效单位保留的精度相同。图5是RLS-NSGA-Ⅱ使用了有效单位保留和不使用有效单位保留的对比图。

图5 使用有效单位保留对比
其中不使用有效单位保留的个体为1 416个,使用有效单位保留的个体为32个,可以看到,使用了有效单位保留后,解集的数量大幅减少,在一定程度上减小了算法搜索的压力。虽然可供选择的个体变少了,但更加符合实际电机优化的需要,为后期的最优个体选择带来了方便。
2 RLS-NSGA-Ⅱ算法
为了解决传统NSGA-Ⅱ对局部范围的Pareto最优面搜索能力较差的问题,本文提出一种基于改进NSGA-Ⅱ的局部范围搜索的算法RLS-NSGA-Ⅱ。RLS-NSGA-Ⅱ在NSGA-Ⅱ的优化空间中选择某一局部区域进行搜索,采用了正态分布交叉算子、极限优化变异算子和最小单位变异算子,并结合永磁辅助开关磁阻电机的实际情况,采用了有效单位保留策略,使得RLS-NSGA-Ⅱ比NSGA-Ⅱ有更好的搜索能力。由于RLS-NSGA-Ⅱ在局部区域搜索,可以平衡采用新交叉算子和变异算子带来的计算量增大的问题。
2.1 局部范围搜索
2.1.1 正态分布交叉算子
传统的NSGA-Ⅱ采用模拟二进制(SBX)交叉算子,本文采用随机搜索范围更广、搜索能力更强的正态分布交叉算子(NDX)[15]。其交叉过程如下。首先产生一个随机数t∈(0,1]。
当t≤0.5时,则:

(1)
当t>0.5时,则:

(2)
式中:p1,i和p2,i分别为父代1和父代2的第i个染色体;x1,i和x2,i分别为子代1和子代2的第i个染色体;|N(0,1)|为标准正态分布随机变量。
2.1.2 极限优化变异算子
传统的NSGA-Ⅱ变异策略只对一个决策变量进行变异,RLS-NSGA-Ⅱ变异策略为每个决策变量分别进行变异,即极限优化变异[16]。极限优化变异能够有效提高局部搜索能力[17],其具体方法如下。设当前目标变异解为X=(x1,x2,…,xv),v为决策变量的个数,极限优化变异公式为

(3)
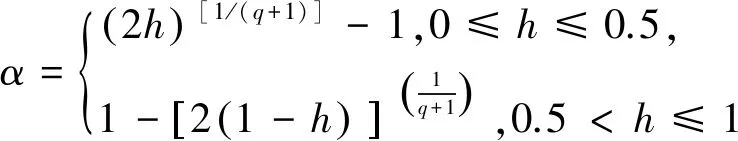
(4)
βmax(xi)=max[xi-li,ui-xi],1≤i≤v
(5)
式中:xi为未变异的决策变量;x′i是变异后的决策变量;h为0~1的随机数;q为正实数,其决定了变异曲线的形状,因此称为形状参数,本文q设置为11;βmax(xi)为当前目标变异解的决策变量可变动的最大值;α为随机变量;li为第i个决策变量的下界;ui为第i个决策变量的上界。
经过极限变异后,一个父代个体可以产生v个不同的子代个体。极限优化变异的搜索距离较小,而搜索范围较广,可以搜索到目标周围可能存在的可行解。本文的极限优化变异针对的是拥挤度较大的前20%的个体。
2.1.3 最小单位优化变异
前文介绍了有效单位的保留。本文在极限优化变异的基础上加入最小单位变异,通过对染色体施加最小单位的变异量,起到增强其局部搜索能力的作用。最小单位代表着优化的精确度,精确度越高,则Pareto解集越多。对决策变量进行最小单位变异有利于增加变异的有效搜索能力。变异的最小单位由下式决定:

(6)
式中:real_max、real_min分别为决策变量的实际最大值和实际最小值;Sd表示有效位数,代表着精确位数,例如精确位为保留小数点后一位时是0.1,保留小数点后两位时是0.01。
由此提出一种基于单位优化变异的变异算子,如下:
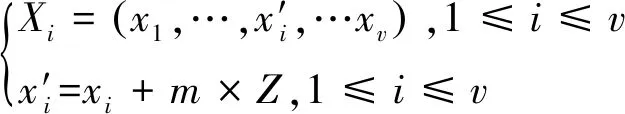
(7)
式中:Z是整数,可以根据实际情况设置为-2、-1、1或者2等整数;m为变异的最小单位。
该变异算子的最大优势是以最小精度为变异单位,搜索个体周围的可行解。
2.2 局部范围和最优个体的选取
2.2.1 选取局部范围
以本文的三目标电机参数优化为例,局部搜索优化原则是在降低转矩脉动的基础上,尽量减少平均转矩的降低[18],效率的选取则优先级较低,因为效率主要是用于观察损耗的变化。在RLS-NSGA-Ⅱ运行之前,使用者需要设定转矩脉动的上限、下限和平均转矩的下限。局部范围搜索的选择过程示意图如图6所示,为方便理解,图6的右视图如图7所示,在转矩脉动上、下限之间且在平均转矩下限之上的个体即是符合要求的个体。

图6 局部范围选择示意图

图7 右视图
2.2.2 最优个体的选取
由图6可知,在NSGA-Ⅱ算法得到的全局Pareto解集中,随着转矩脉动的降低,电机效率和平均转矩的数值也在降低,目标之间相互制约。在图6中,随着转矩脉动减小,平均转矩降低的速度逐渐加快。在得出一组局部范围个体后,需要根据需求选出最优的个体,但是选择最优个体主要依靠决策者的个人偏好。为了便于后面的参数优化对比,这里给出一种简单的最优个体选取公式:

(8)

(9)
f=fripple+ftorque
(10)
式中:fripple、ftorque和f分别是转矩脉动、平均转矩和个体的适应值;Max-ripple、Min-ripple和Ch-ripple分别是转矩脉动的最大值和最小值以及个体的转矩脉动;Max-torque、Min-torque和Ch-torque分别是平均转矩的最大值、最小值和平均值。
由式(8)可知,转矩脉动越小,则该个体的适应值越大,其被选为最优个体的概率就越大。由式(9)可知,平均转矩越大,该个体的适应值越大,其被选为最优个体的概率就越大。式(10)表明,个体的适应值是转矩脉动适应值和平均转矩适应值之和,通过这种方法可以较好地平衡转矩脉动和平均转矩之间的优化矛盾。尽管效率与转矩脉动和平均转矩之间也有优化矛盾,但本文未将效率考虑到最优个体的选取过程中。
2.3 RLS-NSGA-Ⅱ算法流程
根据NSGA-Ⅱ求出Pareto解集的大致分布,选择具体的转矩脉动上、下限和平均转矩的下限等参数,设定种群个数和最大迭代次数,RLS-NSGA-Ⅱ的具体算法流程如下。步骤1:设置RLS-NSGA-Ⅱ的参数;步骤2:初始化,产生符合要求的解集作为初代父代解集;步骤3:对父代解集进行正态分布交叉和变异,并对拥挤度大的个体进行极限优化变异和最小单位优化变异,产生子代解集;步骤4:合并父代解集和子代解集,进行非支配排序;步骤5:记录合并解集中Pareto等级为1且符合要求的个体,并选择局部范围内的解集作为下一代的父代解集;步骤6:重复步骤3~步骤5直到完成迭代次数;步骤7:对记录的解集进行非支配排序,挑选其中Pareto等级为1的个体作为最优解集。
RLS-NSGA-Ⅱ在局部范围内进行优化,使用改进的交叉和变异方式,可以扩大解集的搜索范围得到更多的个体,使搜索能力和收敛性得到提高。
3 优化算法仿真与电机参数优化
3.1 优化算法仿真
ZDT系列函数和DTLZ函数广泛应用于多目标函数的性能测试。为了测试本论文提出的RLS-NSGA-Ⅱ的性能,采用双目标ZDT系列函数(ZDT1、ZDT2和ZDT3)和三目标DTLZ系列函数(DTLZ2)进行仿真,将结果与传统的NSGA-Ⅱ进行对比。本文采用MATLAB R2016a版本,处理器为3.30 GHz,8.00 GB内存。
评价函数使用收敛性度量指标γ,γ表示测试解集与真实Pareto解集最优前沿的逼近程度,其计算式如下:
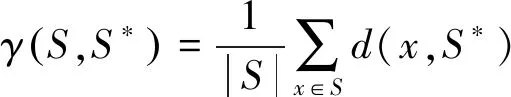
(11)
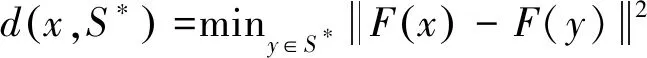
(12)
式中:x是测试算法的解向量;S是测试算法的解集;S*是真实Pareto解集;d(x,S*)表示测试算法得出的解集与真实Pareto解集的距离最小值;F(x)为算法求得的非支配解的位置;F(y)为真实Pareto最优解前沿采样点的位置。
该评价函数表明,当测试算法得出的解集越逼近真实Pareto解集时,γ值越小。因此,该评价函数可以用来测试算法的收敛能力。
为对比RLS-NSGA-Ⅱ和传统NSGA-Ⅱ的收敛效果,将RLS-NSGA-Ⅱ与NSGA-Ⅱ分别独立运行100次,记录其收敛性度量指标γ的数值,运行参数是:NSGA-Ⅱ种群数量500,迭代次数500;RLS-NSGA-Ⅱ的种群数量为100,迭代次数500。对两算法得出的γ值进行独立样本t检验[19],得出两样本的显著性差异,仿真数据如表3所示。

表3 算法仿真数据
从表3可以看出,RLS-NSGA-Ⅱ相比NSGA-Ⅱ在测试函数ZDT2、ZDT3和DTLZ2中有着极显著的差异(P值小于0.001),而在测试函数ZDT1中则不显著(P值大于0.05),但RLS-NSGA-Ⅱ得出的γ平均值仍然小于NSGA-Ⅱ的。
测试函数的Pareto前沿图如图8~图12所示。在ZDT1、ZDT2和ZDT3两目标函数图中,RLS-NSGA-Ⅱ得出的Pareto前沿比NSGA-Ⅱ得出的更靠近真实Pareto前沿,说明其可以较为稳定地收敛到真实Pareto前沿;在DTLZ2三目标函数图中,RLS-NSGA-Ⅱ得出的Pareto前沿比NSGA-Ⅱ得出的更靠近Pareto前沿,并且RLS-NSGA-Ⅱ的个体相比NSGA-Ⅱ更均匀地分布在Pareto前沿。

图8 ZDT1的Pareto前沿图

图9 ZDT2的Pareto前沿图
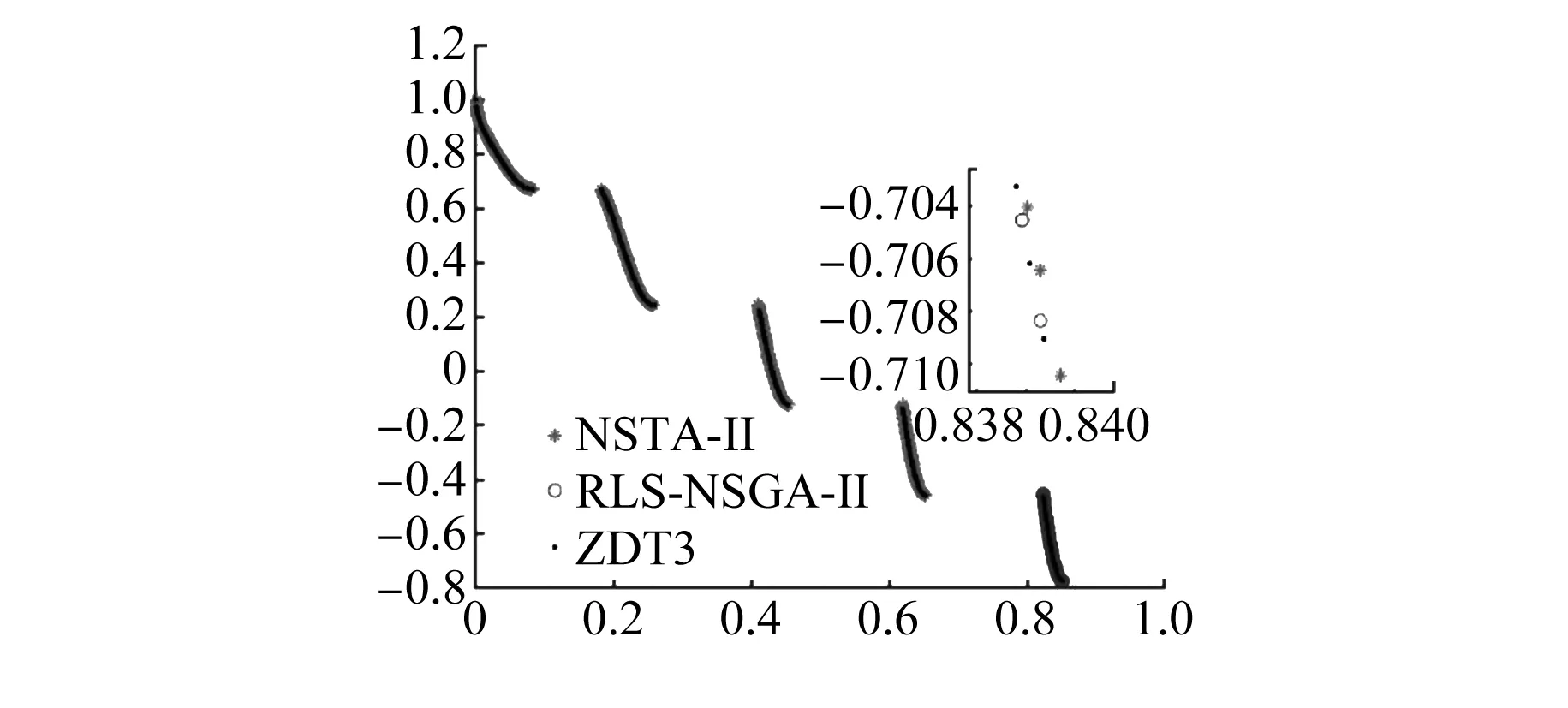
图10 ZDT3的Pareto前沿图

图11 DTLZ2的Pareto前沿图

图12 DTLZ2局部对比的Pareto前沿图
通过NSGA-Ⅱ与RLS-NSGA-Ⅱ的对比可以看到,RLS-NSGA-Ⅱ拥有比NSGA-Ⅱ更强的局部收敛能力,能够搜索到质量更好的Pareto解集,而且从搜索的局部区域来看,RLS-NSGA-Ⅱ在Pareto前沿的分布也更好。
3.2 永磁辅助开关磁阻电机优化
3.2.1 电机多目标优化对比
NSGA-Ⅱ得出的全局Pareto最优面如图13所示,其中种群数量为1 000,迭代次数为500。全局最优个体的决策变量是匝数70匝、电流30 A、开通角-1°、关断角7.8°和极靴角2°,目标函数的参数是转矩脉动51.74%、效率78.92%、平均转矩27.328 4 N·m。

图13 NSGA-Ⅱ得出的全局Pareto最优面
在实际电机优化中,为了使RLS-NSGA-Ⅱ求出的解集数量尽可能多,在迭代选择过程中将转矩脉动范围扩大10%,将平均转矩的下限降低3%。表4是RLS-NSGA-Ⅱ的7组试验参数设置。对NSGA-Ⅱ得出的全部解集进行表4的范围设置,与RLS-NSGA-Ⅱ得出的最优解集进行对比,得出的局部Pareto解集如图14所示。

表4 RLS-NSGA-Ⅱ的参数设置

图14 局部Pareto解集对比
由图14可得到表5,搜索到的个体数量代表搜索能力的强弱,是否被支配代表收敛能力的强弱。从表5可以看到,在第1、2、4、5组中,有一个NSGA-Ⅱ搜索到的个体被RLS-NSGA-Ⅱ搜索到的个体所支配;在第3、7组中,有三个NSGA-Ⅱ搜索到的个体被RLS-NSGA-Ⅱ搜索到的个体所支配;在第6组中,没有NSGA-Ⅱ搜索到的个体被RLS-NSGA-Ⅱ搜索到的个体支配。同时RLS-NSGA-Ⅱ搜索到的个体比NSGA-Ⅱ搜索到的个体更多,这说明RLS-NSGA-Ⅱ的搜索能力和局部收敛能力更强。
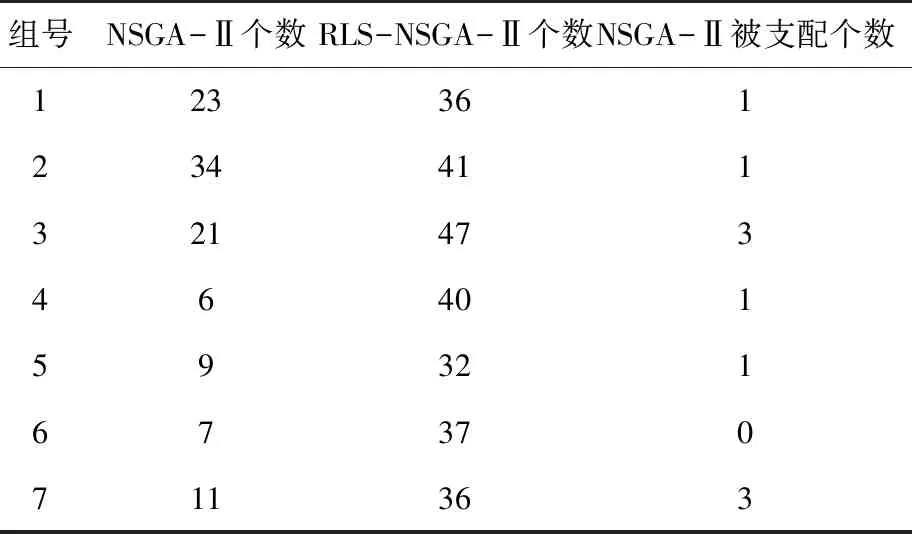
表5 局部搜索能力对比
使用前文提出的最优个体选取方案[式(8)~(10)],挑选出局部最优的个体,表6和表7分别为NSGA-Ⅱ和RLS-NSGA-Ⅱ的7组试验结果,其中第1、3、5组得出的最优个体相同。第2、4、7组RLS-NSGA-Ⅱ得到的最优个体相比NSGA-Ⅱ的转矩脉动更小,但效率和平均转矩不如NSGA-Ⅱ的。其中第2组在关断角延后0.1°和极靴角增加0.1°后,转矩脉动降低3.44%,而效率和平均转矩分别降低了0.93%和0.79%;第4组在极靴角增加0.1°后,转矩脉动降低了2.65%,而效率和平均转矩分别降低了0.59%和0.89%。第6组在匝数增加1匝和关断角延后0.1°后,RLS-NSGA-Ⅱ得到了比NSGA-Ⅱ转矩脉动低0.12%且平均转矩高0.11%的优秀个体。
在使用有效单位保留的NSGA-Ⅱ与RLS-NSGA-Ⅱ进行对比后可以看到,RLS-NSGA-Ⅱ有着更强的局部范围搜索能力,可以搜索到NSGA-Ⅱ搜索不到的优秀个体,加上引入的最小单位优化变异,使得RLS-NSGA-Ⅱ可以局部搜索到解集周围的优秀个体,而且RLS-NSGA-Ⅱ可以搜索到能支配NSGA-Ⅱ搜索结果的个体。综上所述,RLS-NSGA-Ⅱ相比NSGA-Ⅱ有着更强的搜索能力和收敛性。尽管如此,算法搜索出的依然是理论值,接下来将利用有限元软件进行仿真。

表6 NSGA-Ⅱ的1~7组试验数据

表7 RLS-NSGA-Ⅱ的1~7组试验数据
3.2.2 电机有限元仿真对比
将NSGA-Ⅱ局部最优第6组、RLS-NSGA-Ⅱ第6组和NSGA-Ⅱ全局最优的参数代入Maxwell软件中进行仿真[20],仿真结果如表8所示。
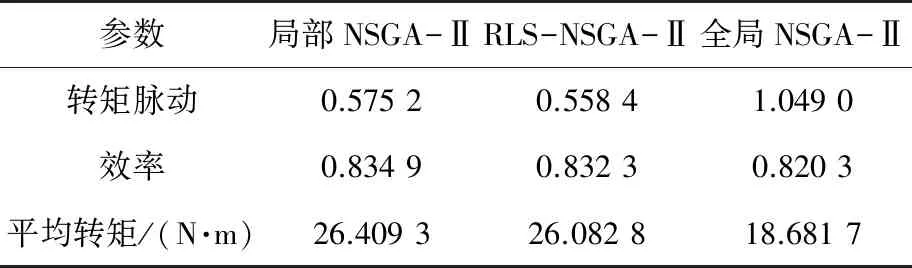
表8 有限元仿真数据对比
将有限元仿真结果与多目标优化结果对比可以看到,局部NSGA-Ⅱ、RLS-NSGA-Ⅱ和全局NSGA-Ⅱ的转矩脉动在有限元仿真的数值上比算法得出的值分别高19.1%、15.7%和3.6%;效率上分别高5.4%、6.3%和0.4%;平均转矩的差别不大,基本可以忽略。
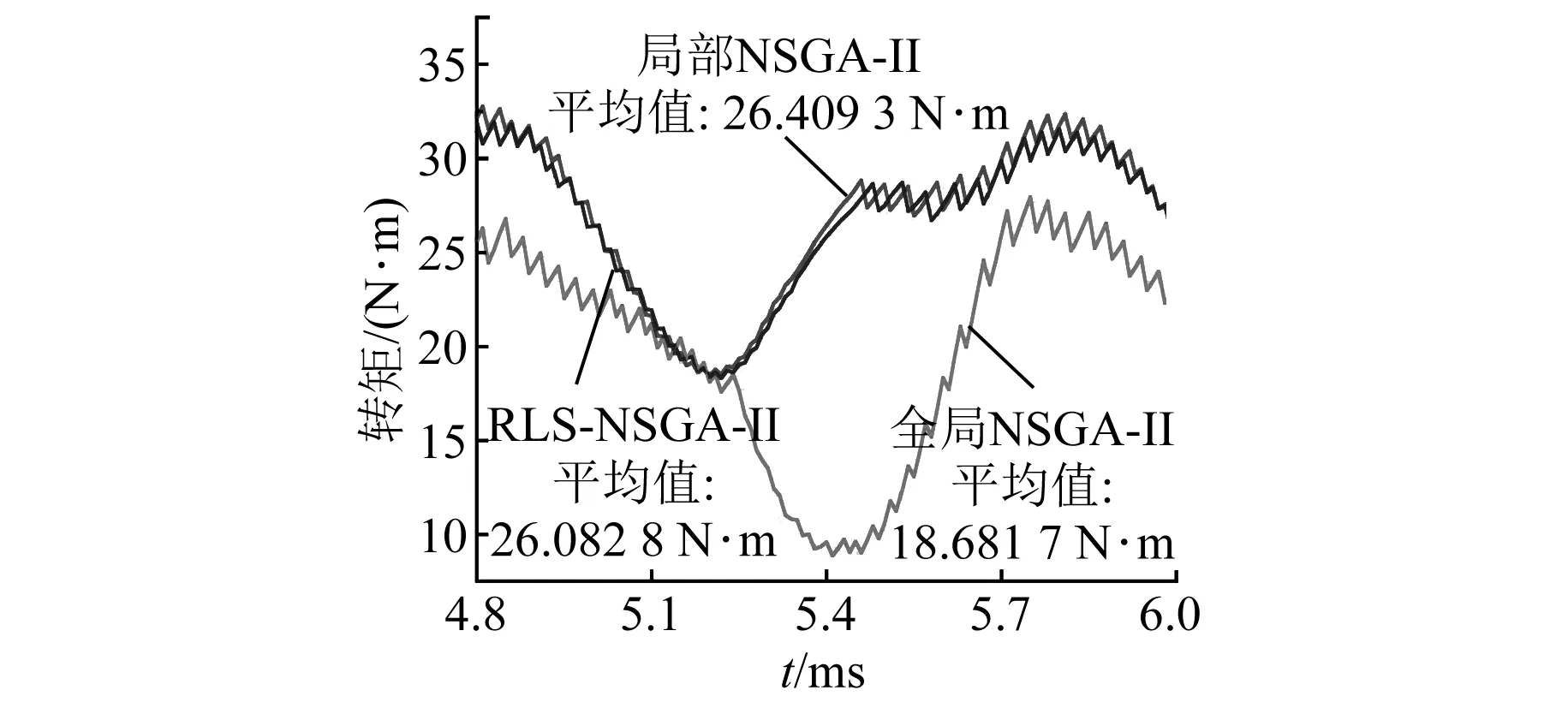
图15 转矩仿真对比图
三组有限元仿真图如图15~图17所示,图15~图17中截取了电机处于稳定时的状态。在图15转矩仿真对比图中可以看到,局部搜索得到的结果相比全局搜索在转矩脉动没有太大变化的情况下,平均转矩得到较大的提升,并且RLS-NSGA-Ⅱ相比局部NSGA-Ⅱ在平均转矩降低了1.2%的情况下转矩脉动降低了2.9%,这说明RLS-NSGA-Ⅱ拥有更强的搜索能力。在图16铁损对比图中可以看到,RLS-NSGA-Ⅱ比局部NSGA-Ⅱ匝数多1匝且关断角延后0.1°,而铁损比局部NSGA-Ⅱ小。在图17铜损对比图中可以看到,RLS-NSGA-Ⅱ的铜损最大,这主要是由电流的导通时间延长带来的。从转矩对比图和损耗对比图来看,RLS-NSGA-Ⅱ算法相比局部NSGA-Ⅱ和全局NSGA-Ⅱ在局部区域寻优中,搜索更优解的能力更加优秀。

图16 铁损对比图
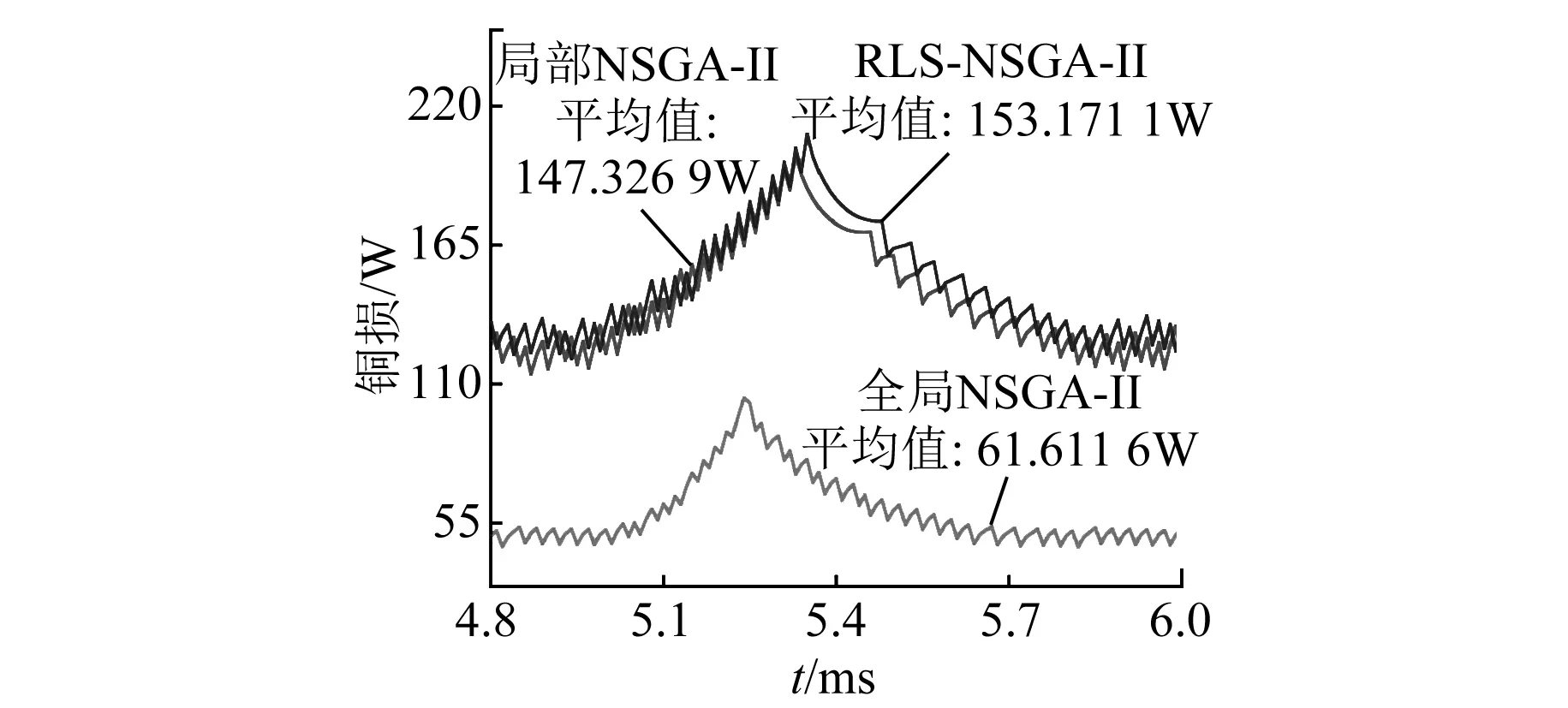
图17 铜损对比图
从有限元仿真来看,多目标优化与有限元仿真的结果是相近的,具有较好的拟合程度,多目标优化的结论可以在有限元仿真中得到验证,可以一定程度上预测有限元仿真的结果,这对电机结构和控制参数优化的提升是巨大的。在接下来的研究中,将继续对RLS-NSGA-Ⅱ进行符合工程实际的优化设计,以便提高电机本体设计的效率和有效性。
4 结 语
本文针对6/20永磁辅助开关磁阻电机参数优化提出了基于NSGA-Ⅱ改进得到的RLS-NSGA-Ⅱ,在引入了正态分布算子和对拥挤度大的个体进行极限优化变异和最小单位优化变异的基础上,进行局部寻优,并使用有效单位保留策略,使算法搜索到的解集参数更加符合实际需求。
使用RLS-NSGA-Ⅱ进行优化算法仿真和永磁辅助开关磁阻电机参数优化试验。在评价函数测试中,通过使用收敛性度量指标γ,证明了RLS-NSGA-Ⅱ拥有优秀的收敛速度和收敛能力,验证了RLS-NSGA-Ⅱ的有效性。在电机多目标优化对比中,第6组中RLS-NSGA-Ⅱ搜索到了37个解集,远多于NSGA-Ⅱ的7个,说明本算法的搜索能力强于NSGA-Ⅱ。在电机参数优化试验中,使用有限元仿真软件对最优个体进行仿真,RLS-NSGA-Ⅱ相比局部NSGA-Ⅱ在平均转矩降低了1.2%的情况下转矩脉动降低了2.9%,这说明RLS-NSGA-Ⅱ拥有更强的搜索能力,验证了本算法有更为优越的最优解搜索能力。尽管仿真中一些运行数据的实际值与理论值存在误差,但总体与理论值差别不大。在后续的研究中,将会考虑减小理论值与实际值之间的误差,为电机的结构优化和控制参数优化提供更好的参考。

