求解逆特征值问题的全局性非精确牛顿类方法*
沈卫平, 王 悦
(浙江师范大学 数学与计算机科学学院,浙江 金华 321004)
0 引 言

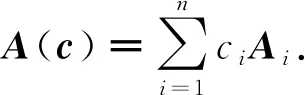
(1)
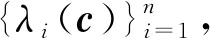
称c*为该逆特征值问题的解.该逆特征值问题的应用十分广泛,如逆Strum-Liouville′s问题、逆Toeplitz eigenvalue问题、核光谱和分子光谱问题、反振弦问题等[4-16].
众所周知,求解该逆特征值问题等价于求解如下非线性方程组问题[17-18]:
基于这种等价关系,求解一般非线性方程组的牛顿法可用于求解该逆特征值问题[19].虽然牛顿法的收敛速度是二阶的,但它的每一个迭代步骤中均需要计算矩阵A(ck)的特征向量.当矩阵的规模n很大时,就需要很大的运算量.因此,文献[19]提出了求解逆特征值问题的牛顿类方法及Cayley变换法.相较于牛顿法,这2种方法在保持二阶收敛速度的同时,又避免了求解特征向量.之后,很多学者针对这2种方法的收敛性及其非精确形式进行了研究[1-2,20].除了上述提到的方法外,还有一些方法在降低运算的难度与加强算法的稳定性方面也有显著的成效,例如文献[3,21]中的Ulm类方法.
但这些方法仅仅具有局部收敛性,只有在解的附近选取初值才能保证迭代序列收敛.基于文献[19]中的Cayley变换法,文献[22]提出了一种求解逆特征值问题的全局性算法.即使初值离解很远,该全局算法产生的迭代序列也能收敛.一个自然的问题是,能否基于文献[1,19]中的(非精确)牛顿类方法,构造一种新的具有全局收敛性质的(非精确)牛顿类方法.
本文提出了一种用以求解逆特征值问题的全局性非精确牛顿类方法.不同于文献[22]中的全局算法,本文的全局算法通过反幂法获得近似特征向量,并采用经典回溯法进行全局化.在一定的条件下,给出了该全局算法的收敛性分析,并证明了它的收敛阶.最后,通过数值例子验证了该算法的全局收敛性质及其收敛阶.
1 全局性非精确牛顿类方法

算法1全局性的非精确牛顿类方法

ρ(c0)=[ρ1(c0),ρ2(c0),…,ρn(c0)]T=[λ1(c0),λ2(c0),…,λn(c0)]T;
计算雅可比矩阵J(c0),其元素为
求解雅可比方程
J(c0)c1=λ*.
(2)
2)对于k=1,2,…直到ck收敛,具体步骤如下:
①非精确求解方程

(3)
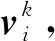

(4)
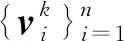
且令ρ(ck)=[ρ1(ck),ρ2(ck),…,ρn(ck)]T.
④计算近似雅可比矩阵Jk,其元素为
⑤非精确求解雅可比方程

(5)
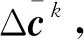
其中,

(6)
⑦若

(7)
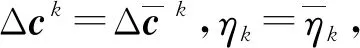
⑧计算下一个迭代点:ck+1=ck+Δck.
注1本文提出的算法与文献[22]中的算法的最大区别在于得到近似特征向量的方式不同.本文的算法利用反幂法得到近似特征向量,而文献[22]的算法则是基于Cayley变换求得近似特征向量.
2 收敛性分析
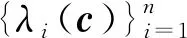
[J(c)]ij=(qi(c))TAjqi(c), 1≤i,j≤n.
需要引进下面几个引理.其中,引理1的证明可参阅文献[23]中的定理4.7;引理2及引理3的证明分别类似于文献[22]中的引理4及引理6;引理4及引理5的证明分别类似于文献[1]中的引理4.1及引理4.2.为了节省篇幅,将其证明省略.
引理1[23]任意ε>0,存在充分小的正数δ0,对任意k∈N,当‖Δck‖≤δ0时,
‖ρ(ck+Δck)-ρ(ck)-JkΔck‖≤ε‖Δck‖.

‖ρ(ck)-λ*+JkΔck‖≤ηk‖ρ(ck)-λ*‖;
(8)
‖ρ(ck+Δck)-λ*‖≤(1-t(1-ηk))‖ρ(ck)-λ*‖.
(9)
引理3[22]假设k∈N且近似雅可比矩阵Jk可逆,则
‖Δck‖≤τk(1-ηk)‖ρ(ck)-λ*‖.
(10)
引理4[1]设k∈N且设γ为任意正数.若
则
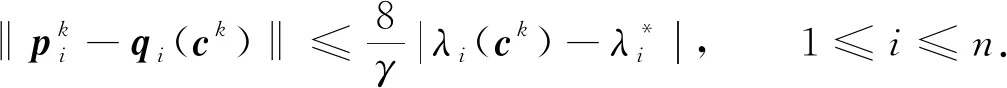
(11)
引理5[1]存在正数δ1,ξ0与γ,对任意k∈N,当‖ck-c*‖≤δ1时,下列式子成立:
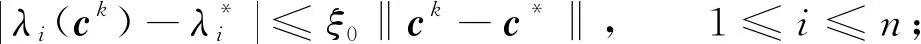
(12)
‖qi(ck)-qi(c*)‖≤ξ0‖ck-c*‖, 1≤i≤n;
(13)
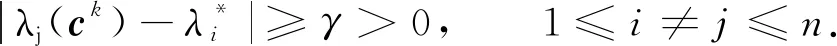
(14)
命题1设K1为任意正整数,则存在正数δ2及ξ(不依赖于K1),若

(15)
且
‖ck-c*‖≤δ2, ∀k≥K1,
(16)
则对任意k≥K1,式(12)、式(14)及下面2个式子成立:
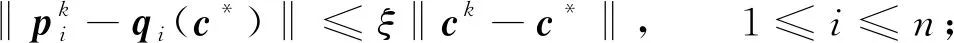
(17)
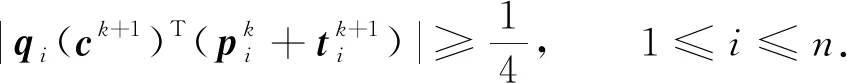
(18)
证明设正数ξ0,γ及δ1为引理5中的常数.令
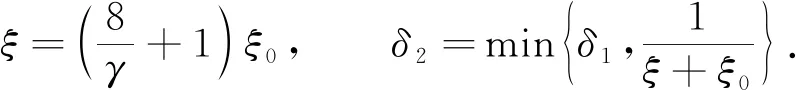
(19)
下证ξ及δ2即为满足命题1结论的常数.为此,假设式(15)及式(16)成立.由式(16)及δ2的定义,并利用引理5可知,对任意k≥K1,式(12)~式(14)均成立.接下来利用数学归纳法证明对任意k≥K1,式(17)与式(18)成立.为简便起见,设1≤i≤n.显然,由式(15)知,当k=K1时,式(17)成立.根据范数的三角不等式,有
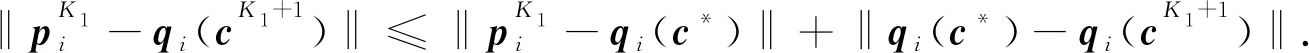
(20)
于是,结合式(15)和式(13)(k=K1+1)可得
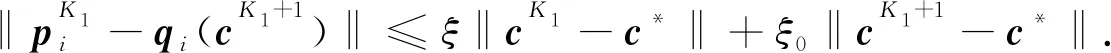
(21)
进一步,再利用式(16)和δ2的定义,容易推得
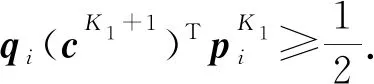
从而,当k=K1时,式(18)成立.
假设当k≤l-1时,式(17)及式(18)成立.于是,应用引理4并结合式(12)(k=l),有
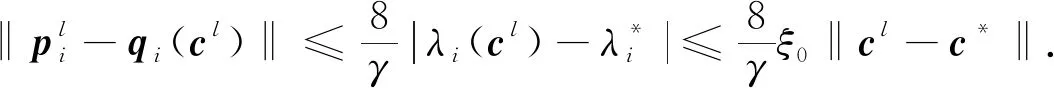
(22)
因此,结合式(13)及ξ的定义,可得
也就是说,当k=l时,式(17)成立.注意到当k=l时,式(18)的证明完全类似于其k=K1时的证明,考虑到篇幅问题,笔者省略了这部分的证明.于是,命题1得证.
为了证明全局性非精确牛顿类方法的全局收敛性和收敛阶,需要引入下面3个引理.其中,引理6的证明可以参阅文献[1]中的引理4.4;引理7及引理8 的证明可以分别参阅文献[22]中的推论7和引理9.
引理6[1]对任意k∈N,由算法1产生的近似雅可比矩阵Jk满足

(23)
引理7[22]设k∈N.若ρ(ck)-λ*≠0且近似雅可比矩阵Jk可逆,则当算法1中步骤⑦的内循环停止时,
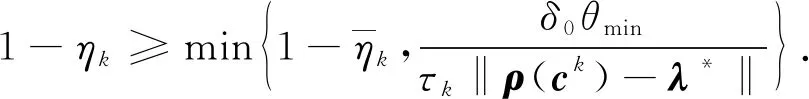
(24)

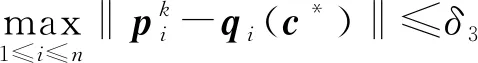

(25)
下面给出本文的主要定理.
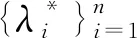

(26)
则当k→∞时,ck→c*且ρ(ck)→λ*,并且序列{ck}至少具有β阶的收敛速度.

下面利用反证法证明序列{ck}的收敛性.假设当k→∞时,ck→/c*,则存在δ5∈(0,δ4)和子列{ckt},使得ckt∉B(c*,δ5),t=1,2,….又因为c*是序列{ck}的聚点,故存在序列{kj}⊂N,使得当j→∞时,ckj→c*.选择lj>0满足kj+lj 结合式(25)可知,对任意的k≥K2, (27) 又因为ck+1=ck+Δck,所以存在充分大的正整数K3≥K2,对任意的j≥K3,有 (28) 其中倒数第2个不等式可由引理3推得.由式(9)易得 因此, (29) 另一方面,因为t,ηk∈(0,1),所以由式(9)可知 ‖ρ(ck+1)-λ*‖≤‖ρ(ck)-λ*‖, ∀k∈N. 因此, (30) 于是,结合式(28)~式(30),有 (31) 又因为当j→∞时,有ckj→c*,所以,‖ρ(ckj)-λ*‖-‖ρ(ckj+1)-λ*‖→0,得到矛盾.因此,假设不成立.从而,当k→∞时,ck→c*. 接下来证明当k→∞时,ρ(ck)→λ*.由定理1条件并应用命题1可得,对任意k≥K2,式(12)、式(14)、式(17)及式(18)成立.于是,应用引理4,当k≥K2+1时, (32) 因为 (33) 因此,利用式(12)、式(32)及式(33),对任意k≥K2+1, (34) 又因为 (35) 因此,由式(34)和式(35)可推出 ‖ρ(ck)-λ*‖≤ρ‖ck-c*‖, ∀k≥K2+1. (36) rk=JkΔck+ρ(ck)-λ*. (37) 那么,根据算法1中的步骤⑤可知 (38) 注意到Δck=ck+1-ck和Jkck=ρ(ck).将这2个式子代入式(37),计算可得 Jk(ck+1-c*)=rk-(Jkc*-λ*). (39) ‖ck+1-c*‖≤2‖J(c*)-1‖(‖rk‖+‖Jkc*-λ*‖). (40) 应用引理6,并结合式(17)及条件ck∈B(c*,δ4),有 (41) 另一方面,利用式(38)、式(6)和式(36),容易推得 (42) 将式(41)与式(42)代入式(40),可得 从而,序列{ck}的收敛速度至少是β阶的.定理1证毕. 下面将通过若干个数值例子验证全局性非精确牛顿类方法的理论结果.例1研究了逆Toeplitz 特征值问题[16],例2考虑了Toeplitz-plus-Hankel逆特征值问题[7]. 所有的数值实验均采用Matlab中的qmr函数求解算法1中的式(2)、式(3)及式(5).另外,当 给定的精确解与精确特征值向量分别为 c*=(2,3,4,5,6)T,λ*=(-5.236 1,-1.587 6,-0.763 9,-0.555 5,18.143 1)T. 例1考虑以下3个不同的初始值:1)c0=(1,2,3,4,5)T;2)c0=(21,38,46,63,81)T;3)c0=(150,159,168,170,180)T.表1~表3列出了在这3个初始值下,该全局算法的数值实验结果. 表1 初值为c0=(1,2,3,4,5)T的数值实验结果 表2 初值为c0=(21,38,46,63,81)T的数值实验结果 表3 初值为c0=(150,159,168,170,180)T的数值实验结果 给定的精确解与精确特征值分别为: c*=(15,16,17,18,19)T,λ*=(-59.951 4,-24.048 5,-19.696 4,23.258 6,53.437 7)T. 考虑以下3个不同的初始值:1)c0=(31,32,33,34,35)T;2)c0=(35,45,60,80,95)T;3)c0=(150,159,168,175,185)T.表4~表6列出了在这3个初始值下,该全局算法的数值实验结果. 表4 初值为c0=(31,32,33,34,35)T的数值实验结果 表5 初值为c0=(35,45,60,80,95)T的数值实验结果 表6 初值为c0=(150,159,168,175,185)T的数值实验结果 从上面2个例子的数值实验结果可以看出,即使初始值没有靠近问题的解c*,由算法1产生的序列{ck}依然能收敛至c*,这恰好说明了本文所提出的非精确牛顿类算法的收敛性具有全局性质.同时,从表1~表6中的数据也可以看出序列{ck}的超线性收敛性质.

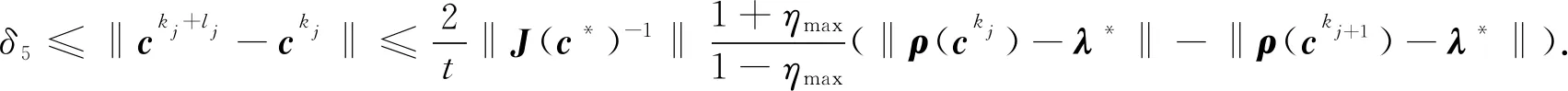
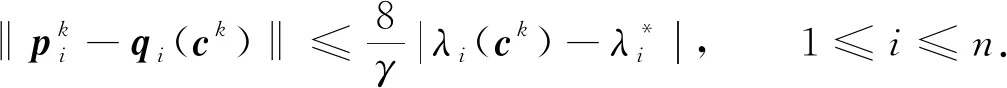
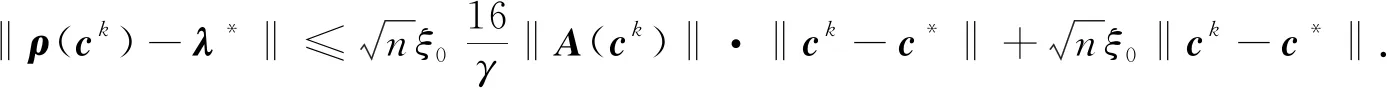



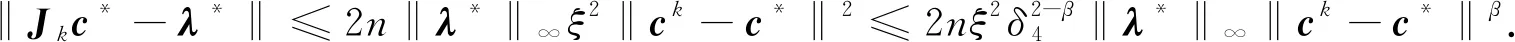

3 数值算例