基于混合粒子群优化的智能电表计量多维数据聚类方法

付文杰，尚晓明，陈 磊，张军朝

（国网河北省电力有限公司，石家庄 050000）

0 引言

伴随电力系统的智能化发展，智能电表计量装置中包含越来越多的多维数据，智能电表计量数据量急剧上涨[1]。聚类算法是依据海量数据中包含的潜在规则，对数据进行分类的信息处理方法。粒子群优化算法应用于聚类算法优化时，通过设置适应度函数交叉操作粒子，提升粒子群算法内粒子种群的多样性，避免聚类算法运行过程中，存在陷入局部最优的情况。

目前针对智能电表计量数据的研究越来越多，智能电表计量数据管理已成为电力领域的研究重点。研究高效的智能电表计量数据处理方法，已成为电力领域数据处理中亟待解决的重要问题。肖勇等人将深度信念网络应用于智能电表数据异常检测中[2]，有效检测智能电表中存在的异常数据，对于提升智能电表数据的应用性提供了有效的理论依据；高欣等人将CVAE-CNN模型应用于智能电表故障分类中[3]，有效识别智能电表中不同类型故障，为智能电表的可靠运行提供依据。以上研究方法实现了智能电表异常以及故障的有效监测，但是无法应用于智能电表多维数据分类中。为了提升智能电表数据的应用性能，研究基于混合粒子群优化的智能电表计量多维数据聚类方法。采用混合粒子群算法对聚类算法进行优化，利用优化后的聚类算法处理智能电表多维计量数据，实现智能电表多维计量数据的有效划分，提升智能电表多维计量数据的应用性。

1 智能电表计量多维数据聚类

1.1 双模组网的智能电表计量数据采集

选取双模组网方式作为智能电表多维计量数据的采集方式，双模组网方式通过无线微功率与载波方式的结合，实现智能电表海量多维计量数据的通讯。智能电表双模组网方式的结构图如图1所示。

图1 双模组网方式

选取现有的电力线缆作为智能电表双模组网方式的电力载波方式。双模组网方式无需设置智能电表计量多维数据通信的通信线路，采用原有的电力线缆进行数据通信，具有较高的通信可靠性。双模组网中的无线微功率利用无线方式完成智能电表数据的宽带连接，具有组网速度快的特点，可以满足智能电表多维计量数据的通信线路切换水平。双模组网方式适用于应用距离较近，未敷设光纤，智能电表较为分散的供电区域。

1.2 基于关联维的智能电表计量数据的混沌特征提取

智能电表计量多维数据具有较高的关联性以及相似性，提取智能电表计量多维数据的混沌特征，为智能电表计量多维数据聚类提供依据。智能电表计量多维数据中的随机点与中心点间距超过所设定距离标准值时，表明该随机点与所选取中心点不存在相关性关系；智能电表计量多维数据中的随机点与中心点间距小于所设定距离标准值，同时距离标准值与间距不为零时，表示该随机点与智能电表计量多维数据的中心点存在相关性[4]。智能电表计量多维数据内与中心点具有相关性的点数量越多时，表示智能电表计量多维数据的多项空间内存在更多的关联维度。

式(1)中，G与Li分别表示赫维赛德函数以及大于两个中心点间距的随机点至中心点距离。

用d(L)表示关联函数，其表达式如式(2)所示：

利用包含集合Q的分数对关联函数进行去重处理。

用W表示智能电表计量数据提取混沌特征距离的标准值，可得设定的距离标准值W表达式如式(3)所示：

式(3)中，v表示关联维数。关联维数可以体现智能电表计量多维数据间的混沌程度，将数据间的混沌程度设置为智能电表计量多维数据的聚类基础。

1.3 混合粒子群优化K-means的计量数据聚类

1.3.1 计量数据的K-means聚类算法

1）完成划分的簇并未空集，簇内的数据需要大于0。

2）所划分的簇内的智能电表计量多维数据与该簇存在唯一的关系性，即智能电表计量多维数据仅可属于一个簇。

K-means聚类算法是利用贪心策略进行数据划分的重要算法，该算法通过迭代更新方式，令聚类结果逼近最优解。K-means聚类算法对智能电表计量多维数据进行聚类的聚类过程如下：

1）随机从智能电表计量多维数据中选取初始簇质心数量为K，所选取初始簇的质心用表示。

2）设置集合Ci为智能电表计量多维数据集Z中，相比于ηj，与ηi距离更近的点的集合。

3）用ηi表示集合Ci内，全部智能电表多维数据的质心，质心ηi的计算公式如式(4)所示：

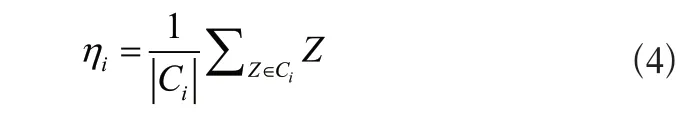
4）重复以上步骤，直至集合C内的数据不再变化为止。

1.3.2 粒子群优化计量数据聚类

设粒子群优化算法内全部粒子在n维智能电表计量数据搜索空间中的运动状态与位置向量以及速度向量相关。用Xi=[xi1，xi2·，··xin]与Vi=[vi1，vi2·，··vin]分别表示粒子群算法的位置向量以及速度向量。

通过粒子群优化算法内粒子的位置变化，表示智能电表计量多维数据聚类问题的可行解。用Pbest=[pi1，pi2·，·pin]与gbest=[g1，g2·，··gn]分别表示粒子群内粒子个体的历史最优解以及全局历史最优解。

粒子群优化算法的粒子速度更新公式如式(5)所示：

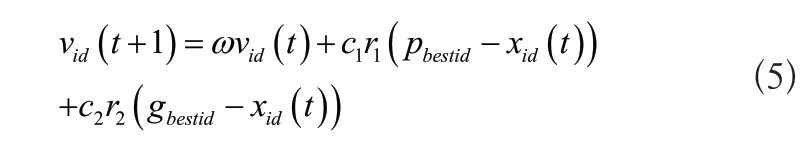
粒子位置更新公式如式(6)所示：

式(6)中，c1、c2与ω分别表示加速度常数以及惯性权重；r1与r2均表示随机常数。

粒子群优化算法的惯性权重线性递减的表达式如式(7)所示：

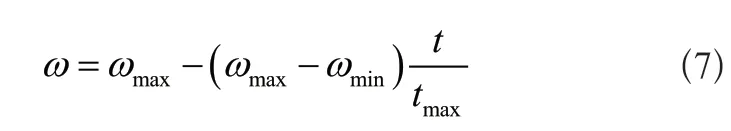
式(7)中，t与tmax分别表示迭代次数以及最大迭代次数，ωmax与ωmin分别表示惯性权重最大值以及最小值。

1.3.3 混合粒子群优化计量数据K-means聚类算法

采用混合粒子群优化算法优化K-means聚类算法，获取智能电表计量多维数据聚类结果。

设置混合粒子群优化K-means聚类算法的适应度函数表达式如式(8)所示：

式(8)中，J表示智能电表计量多维数据聚类的目标函数，设置聚类均方根误差最小作为智能电表计量多维数据聚类的目标函数。聚类目标函数值越小，聚类的适应度值越高。

K-means聚类算法对智能电表计量多维数据进行聚类时，存在容易早熟的情况。粒子群算法内的种群多样性伴随迭代次数的提升而有所下降，无法快速收敛至全局最优解。伴随粒子群算法不断迭代，粒子群优化算法运行速度有所降低。粒子群优化算法的粒子速度下降至0时，粒子群优化算法内的粒子无法继续在智能电表计量多维数据的搜索空间中搜索。为了避免粒子群算法内粒子无法继续搜索，设置阈值εv以及区间为0～1范围内，服从均匀分布的随机变量r3。粒子运动速度vij小于阈值εv时，令vij=r3×vmax，避免粒子早熟情况。粒子以此时的位置在智能电表计量多维数据的搜索空间中重新开始搜寻[5]，以新速度继续搜寻，提升粒子群算法的收敛速度。

选取混沌系统中的Logisic映射方法优化粒子群算法，Logisic映射是混沌空间中的满映射，具有计算量小以及使用方便的特点。Logisic映射表达式如式(9)所示：

式(9)中，μ与θik分别表示控制参数以及混沌特征向量。

引入混沌特征向量，将粒子群优化算法的位置更新公式转化如式(10)所示：

式(10)中，xk表示混沌运算向量映射至[0，1]区间的粒子群向量；xk+1表示加入了随机扰动后的混沌特征向量；λ表示区间为[0，1]的调节系数，该系数可以自适应变化，利用调节系数控制混沌特征向量对粒子群向量的扰动程度。

粒子群算法运行初期时，调节系数λ的值较大，伴随粒子群算法不断运行，调节系数逐渐降低。粒子群算法优化K-means聚类算法，对智能电表计量多维数据进行聚类的调节系数计算公式如式(11)所示。

式(11)中，t与σ分别表示粒子群优化算法的当前迭代次数以及依据智能电表计量多维数据聚类目标函数设置的整数。

将混沌算子引入粒子群优化算法，基于混合粒子群优化的智能电表计量多维数据聚类方法流程如下：

设置智能电表计量多维数据间的混沌程度作为K-means聚类的聚类依据，利用混合粒子群算法优化K-means聚类算法。随机选取粒子，利用混沌算子扰动粒子，所选取粒子设置为粒子群优化算法的个体极值以及全局极值。

从智能电表计量多维数据聚类的解空间[ximin,ximax]中，将所确定粒子的全部分量xi映射至混沌空间表达式如式(12)所示：

将粒子的全部分量映射至混沌空间后，利用式(10)优化x′i。将完成混沌优化的粒子分量逆映射，粒子映射至解空间的表达式如式(13)所示：

采用混沌算子优化粒子群内粒子后，更新粒子位置，直至迭代次数满足最大迭代次数，且智能电表计量多维数据聚类的目标函数满足条件，终止粒子群算法运算，输出智能电表计量多维数据聚类结果。

2 实验分析

为了验证所研究基于混合粒子群优化的智能电表计量多维数据聚类方法对于智能电表计量多维数据的聚类有效性，将该方法应用于某电力企业的智能电表计量数据管理中，通过智能电表计量数据多维聚类结果，提升智能电表计量数据应用性。

该电力企业的智能电表数据管理系统中，智能电表计量多维数据显示界面如图2所示。

图2 智能电表计量多维数据显示界面

通过图2实验结果可以看出，该电力企业的智能电表可以显示不同用户的电压数据、电量数据等不同类型的多维数据。智能电表计量多维数据的聚类方法的聚类性能极为重要。

采用本文方法对其中10个智能电表采集的多维计量数据进行聚类，智能电表数据集的属性如表1所示。

表1 智能电表数据集的属性信息

采用混合粒子群优化方法对智能电表计量的多维数据进行聚类，所获取的关联维数如图3所示，选取文献[2]方法与文献[3]方法作为对比方法。

图3 关联维数对比结果

通过图3实验结果可以看出，采用本文方法对智能电表计量多维数据进行聚类，所获取的关联维数具有较高的稳定性。文献[2]方法以及文献[3]方法对智能电表计量多维数据进行聚类的关联维数波动性较大。图3对比结果有效验证本文方法对智能电表计量多维数据聚类的关联维数具有较高的稳定性，可以满足智能电表计量多维数据聚类的稳定性需求。

采用本文方法对智能电表计量多维数据进行聚类，获取智能电表运行期间，不同时间时，其中三个智能电表的电压数据结果如图4所示。

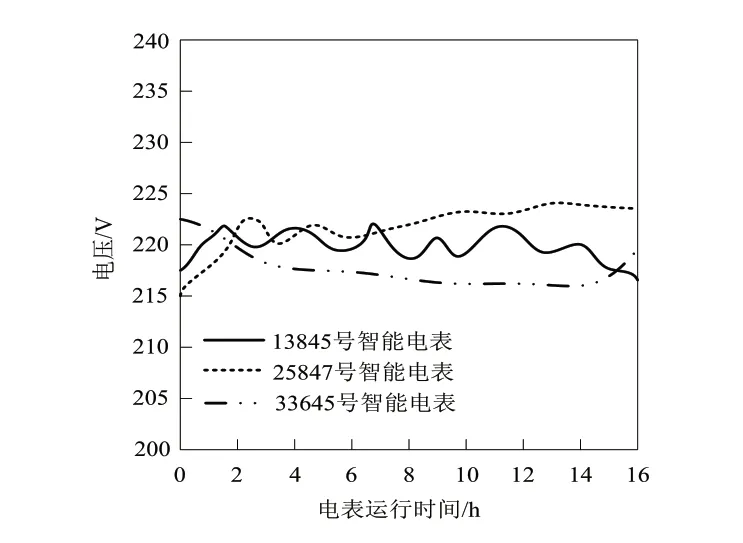
图4 智能电表电压数据聚类结果

通过图4实验结果可以看出，采用本文方法可以实现智能电表计量多维数据的有效聚类，获取智能电表计量多维数据中的电压数据。智能电表管理人员可以依据通过聚类获取的不同智能电表的电压数据，获取用户用电过程中的电压质量。

采用混合粒子群优化对智能电表计量多维数据进行聚类，获取智能电表运行期间，不同时间时，其中三个智能电表的电流数据结果如图5所示。

通过图5实验结果可以看出，采用混合粒子群优化方法可以实现智能电表计量多维数据的有效聚类，获取智能电表计量多维数据中的电流数据。通过图5实验结果可以看出，序号为13845的智能电表于8时存在电流数据异常情况，智能电表计量管理人员可以依据电流变化，明确智能电表的运行状况。

采用混合粒子群优化方法对智能电表计量多维数据进行聚类，获取智能电表运行期间，不同时间时，其中三个智能电表的有功功率结果如图6所示。

图6 智能电表有功功率数据聚类结果

通过图6实验结果可以看出，采用混合粒子群优化方法可以实现智能电表计量多维数据的有效聚类，获取智能电表计量多维数据中的有功功率数据。智能电表管理人员可以依据通过聚类获取的不同智能电表的有功功率，明确用户用电过程中的功率波动情况。

采用混合粒子群优化方法对智能电表计量多维数据进行聚类，获取智能电表运行期间，不同时间段，其中三个智能电表的电量变化如图7所示。

图7 智能电表电量聚类结果

通过图7实验结果可以看出，混合粒子群优化方法可以对智能电表计量多维数据中的电量数据进行聚类，电量数据是智能电表计量数据中的重要数据，混合粒子群优化方法通过聚类获取多维数据中的电表运行的电量数据，智能电表管理人员可以依据聚类结果中的电量数据直观展示用户的用电情况，验证本文方法具有较高的应用性。

4 结语

针对智能电表计量多维数据间的关联程度较高，导致聚类效果较差的缺陷，将混合粒子群优化算法应用于智能电表计量多维数据聚类中，利用混合粒子群优化算法提升聚类算法对智能电表计量多维数据的聚类性能。通过实验验证该方法可以实现智能电表计量多维数据的有效聚类，混合粒子群优化算法可以有效改善聚类算法存在的早熟情况，提升了聚类算法的收敛速度，实用性较高，可以有效提升智能电表计量数据的应用性能。