蒙西地区储能技术经济性优化配置研究
窦东,王雁宇,李欣,杨文生,周文奇,李海清,张士营
(1. 内蒙古电力经济技术研究院,内蒙古 呼和浩特 010040;2. 华能新能源股份有限公司,北京 100036)
0 引言
在“30·60”双碳目标以及构建新型电力系统的背景下,以风光为代表的可再生能源在未来将得到大力发展。蒙西地区作为中国重要的风光基地,提出计划到“十四五”期间2025年新能源装机容量占比将超过50%,成为全区电力的主体能源[1]。与此同时,降低新能源出力波动性、保障新能源高效消纳和提升电力系统的灵活性和安全稳定性等问题亟待解决。灵活的充放电特性使得储能成为改善上述问题的重要调节性资源。研究在满足电网技术需求的同时实现储能的高效、经济性配置,具有重要意义。
目前,国内外学者就储能在不同应用场景下的规划配置、运营管理以及技术经济分析等方面开展了广泛的研究。新能源发电侧,文献[2-6]在考虑风电、光伏出力随机波动性以及电力供需灵活性等因素影响下,提出兼顾经济性和灵活性的多类型储能优化配置方法,以降低新能源出力波动性并提高其利用效率。文献[7-8]将储能和需求响应技术纳入新能源发电优化调度中,提出由储能、发电侧以及需求响应侧构成的联合优化模型,以促进新能源的出力消纳及其经济性运行。在电网侧,文献[9-13]基于电网侧储能技术的需求场景、投资价值,提出电网侧储能的商业运营模式以及选址定容规划模型,用以满足电网侧在不同应用场景下对大规模储能技术进行经济高效运营的需求。在用户侧,文献[14-17]通过构建峰谷电价、实时电价与用户侧储能的成本动态联动模型,提出用户侧储能的经济性优化控制策略,以解决用户侧储能的容量优化配置问题并推进其商业模式的发展。在储能的投资分析方面,文献[18-23]采用全寿命周期成本等方法,考虑商业运营模式、投资成本和经济效益,对多类型储能技术在不同应用场景下的投资经济性、系统价值进行了评估测算。
上述储能规划配置方法在新能源侧多为技术性优化、缺乏经济性优化在电网侧多为电网侧的单方面储能价值测算;用户侧商业模式较为单一、应用场景局限,投资分析方面缺乏包含外部价值的综合价值测算,此外,现有储能的规划配置方案多数为通用性的优化方案,缺少有针对性的具有地区特色的储能经济性配置方案。
综上,本文提出针对蒙西地区的储能技术经济性优化配置模型,以降低风-光出力波动性和最大化储能系统的综合经济价值为目标,为蒙西地区的储能的选型、选址和容量配置提供规划建议。首先,基于蒙西地区的实际情况以及不同类型储能应用场景,提出针对蒙西地区的储能选型选址方案。其次,以最小化风光出力波动性和最大化储能的综合价值(内部价值和外部价值)为目标,构建储能技术经济性优化配置模型,并针对该模型提出基于NSGA-II的求解算法。然后,以蒙西地区某风光接入点为例,计算满足多目标条件下的储能配置方案,以不同的风光占比和储能的电池成本为影响因素,对该模型进行了灵敏度分析。最后,基于上述算例分析,提出了针对蒙西地区的储能经济性配置决策指导方案。
1 蒙西地区储能选址选型研究
1.1 选址研究
对储能的配置位置进行合理规划是降低储能系统投资、提高运行效益以及提升整个系统运行稳定性和资源利用效率的重要手段。文献[24]提出了针对新能源侧储能选址优化的通用性结论:在电力系统中的重要传输节点和可再生能源的发电接入点配置储能可以在兼顾经济性和系统稳定性的因素下达到储能选址配置的最优。因此,本文采用上述结论进行蒙西地区储能选址分析。以《内蒙古电网2021年度运行方式》提供的相关资料为参考依据,蒙西地区的风电、光伏资源主要集中在乌兰察布、包头、巴彦淖尔以及锡林浩特地区,分别占蒙西地区新能源装机容量的23.32%、21.63%、17.86%和15.62%。这些地区的重要传输结点以察右中、百灵、巴中、塔拉等500 kV变电站为主。在兼顾系统稳定性及经济性因素下,重点在上述4个地区的新能源接入点和重要传输节点进行储能配置,具体选址如表1所示。其中,新能源接入点主要为220 kV变电站,重要传输节点为500 kV变电站,部分重要传输节点亦是新能源接入点,不再重复列出。

表1 蒙西地区储能配置选址Table 1 Site selection for energy storage configuration in western Inner Mongolia
1.2 蒙西地区储能选型研究
文献[24]从技术、经济、效率、环境4个维度建立了适应各种场景的储能选型指标体系,通过贝叶斯最优最劣法确定了不同场景下的指标权重,并通过模糊前景理论对储能在各种场景下的选型进行了综合评价,进而得出了储能在各类应用场景的排序,如表2所示。该选型排序研究并未涉及与地区相关的因素,具有一定的通用性,因此本文采用该选型排序结论确定蒙西地区储能类型。

表2 各类应用场景下储能选型排序Table 2 Type selection and sorting for energy storage in various application scenarios
本文主要针对储能降低新能源出力波动性的应用场景进行分析,该应用场景属于辅助服务的应用场景范畴,由表2可知,在蒙西地区配置储能以实现平抑新能源出力波动性的最优储能选择为锂离子储能。本文后续研究中,若无特殊指出,涉及的储能均为锂离子电池储能。
2 储能技术经济性优化配置模型
本文以储能降低风光出力波动性为技术目标,以提升储能系统的综合利润(投资净现值)为经济目标,考虑储能系统的各类约束,实现对储能系统的容量、功率的最优化配置。
2.1 目标函数
2.1.1 技术目标


2.1.2 经济性目标


(2)储能收益。储能的收益测算主要包括自身价值测算和外部价值测算。其收益构成如图1所示。

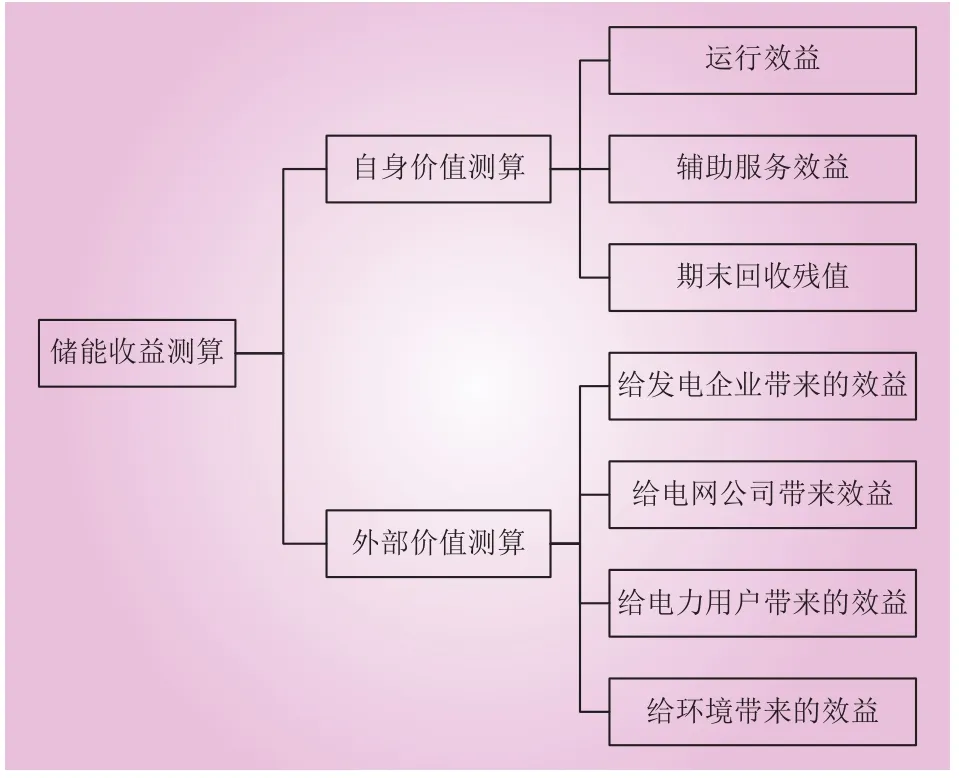
图1 储能的收益构成Fig. 1 Revenue structure of energy storage


2.1.3 多目标函数

2.2 约束条件

2.3 求解算法
储能技术经济性优化模型为多目标优化问题,基于加权法和目标规划算法的传统数学优化方法带有一定的主观性,无法有效求得多目标算法的帕累托最优解集合。NSGA-Ⅱ是目前求解大规模多目标优化模型的有效算法,具有计算速度快、求解精度高、解集收敛性好、可求得帕累托最优解集等特点[27]。基于此,本文采用NSGA-Ⅱ算法对储能技术经济性优化模型进行求解,算法流程图如图2所示。

图2 模型求解流程Fig. 2 Flowchart of model solving
3 算例分析
以蒙西某风光资源丰富地区为例,基于储能经济性优化配置模型,计算分析针对该地区风光出力特性的经济性储能配置方案。
3.1 算例参数设置
该地区的新能源由装机容量为10 MW的风电站和2.5 MW的光伏发电站构成,能统一接入节点A。以季节变化为周期,该地区风、光的典型日出力曲线如图3所示。根据国家《国家发展改革委关于2021年新能源上网电价政策有关事项的通知》,蒙西地区风电、光伏的上网电价为0.278 5 元/(kW·h)。
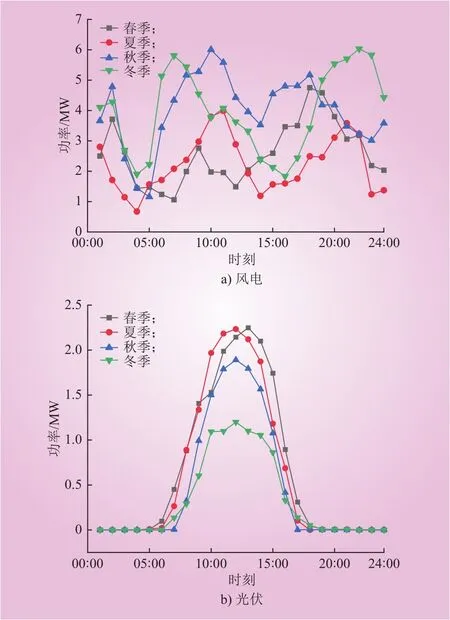
图3 风电及光伏典型日出力曲线Fig. 3 Typical daily output curves of wind power and PV
基于该地区的实际特点,拟在节点A处配置锂离子储能系统,主要为新能源发电端提供辅助服务,因此该储能系统对于发电端的影响为内部价值,对于电网、用户及环境的影响为外部价值。该储能系统寿命为10年,容量衰减系数定为常数1,期末回收残值率为10%。储能的成本及效益计算采用净年值计算方式,贴现率为8%。根据《华北电力调峰辅助服务市场运营规则》,储能系统提供辅助服务的成本为0.4元/(kW·h)。储能系统的其他参数设置如表3所示。

表3 储能系统参数设置Table 3 Parameter setting for energy storage system
在进行储能的收益计算时,储能以平抑新能源发电的波动性为目的向其提供辅助服务,受到技术约束以及蒙西地区低峰谷电价差的限制,不考虑其自身通过电价差赚取收益。此外,储能在发电端运用场景下,用户侧减少的停电损失难以衡量,为用户减少的停电损失不再测算。因此,该储能运用场景下,储能的内部价值测算包括提供辅助服务获利、减少弃风、弃光电量损失以及期末设备残值回收,外部价值测算包括延缓电网投资收益以及环境收益。储能系统主要接入35 kV电压等级的电网中,基于当地35 kV电压等级的电网投资数据,运用文献[28]的电网设备投资计算方法,可测算出该项收益约为1 391.23元/kW。储能系统的环境效益可以量化为减少常规燃煤机组发电过程产生的SO2、CO2等污染物的排放,根据文献[28],其值约为0.12元/(kW·h)。
使用Matlab 2016 b对基于储能技术经济性优化模型的NSGA-II算法进行编程运算,算法采用十进制编码方式。考虑算法解集的收敛时间,参考文献[27]的算法参数设置,对参数进行如下设置:种群规模为300,最大进化代数为100,交叉概 率 为0.9,变异概 率pm=1/n, 其 中 ηc=1/n,ηm=1/n,其他参数使用默认参数。
3.2 算例结果分析
(1)技术性优化结果分析。
经过优化计算,可得到一系列不同风-光波动抑制率下的储能系统功率及容量配置的帕累托最优解集。抑制10 MW风电与2.5 MW光伏联合出力波动性的储能功率与容量配置方案如表4所示。

表4 不同风光出力波动抑制率下储能系统配置方案Table 4 Configuration scheme for energy storage system under different σp
随着风光出力波动抑制率要求的提高,储能的功率、容量配置以及持续时长将快速增长。将风光出力的标准差降低10%最少需要配置0.495 MW/0.736 MW·h的储能,储能占新能源装机容量占比仅为6.13%,持续时间为1.34 h;而将风光出力的标准差降低40%,则至少需要配置1.929 MW/5.724 MW·h的储能,储能占新能源装机容量占比将提升到47.7%,持续时间需要提升到2.67 h。
该地区风-光联合出力曲线可分为峰段(00:00—02:00、09:00—13:00、20:00—22:00)和谷段(03:00—05:00、15:00—19:00、23:00—24:00),为了满足不同风光波动抑制率要求,储能系统在满足经济运行最优的情况下,多次进行充放电操作。帕累托解集得出的不同风光出力波动抑制率下风-光、风-光-储以及储能的出力计划对比情况如图4所示。

图4 不同σp下风-光-储联合出力情况Fig. 4 Wind power-PV-storage joint output under different σp
(2)经济性优化结果分析。
在不考虑储能外部价值的情况下,该储能项目投资经济性分析结果如表5所示。为了更加全面地反映经济性评价结果,表中加入投资回收期与内部收益率的测算分析。随着风光出力波动抑制率的逐渐提高,储能的净现值、内部收益率逐渐下降,投资回收期逐渐提高,投资经济性呈下降趋势。当 σp大于30%时,储能系统的投资将不具有经济性,在规定寿命周期内无法回收成本。

表5 不考虑外部价值的投资经济性分析结果Table 5 Result of investment economy analysis without considering external value
在考虑储能的外部价值的情况下,该储能项目投资经济性分析结果如表6所示。在考虑储能的外部价值情况下,该储能项目将具有良好的投资经济性。当 σp为10%时,该项目的内部收益率高达60.73%,当 σp上升到40%时该项目仍具有18.19%的内部收益率。
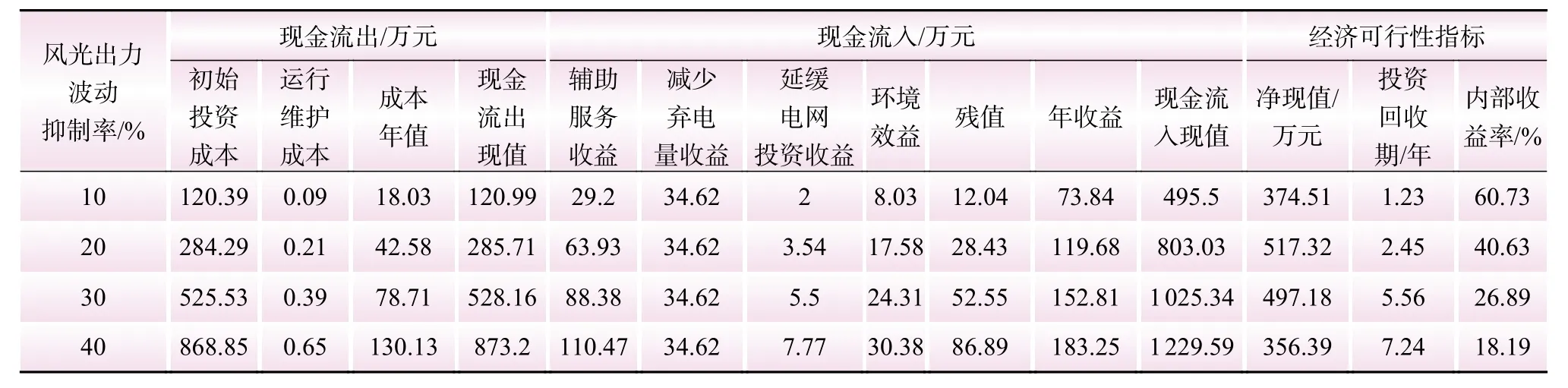
表6 考虑外部价值的投资经济性分析结果Table 6 Result of investment economy analysis considering external value
(3)帕累托曲线。
投资成本是储能规划设计的一项重要经济性指标,基于技术、经济性优化结果可得到储能系统投资成本与风-光-储联合出力标准差之间的帕累托曲线,如图5所示。随着风光出力波动抑制率的不断提高,储能的初始投资成本不断提高,且提高速率逐渐增加。风光出力波动抑制率从5%提升到35%,储能的初始投资成本仅增加658.61万,而从35%提升到60%,储能的初始投资成本增加1 213.02万元,为满足更高的风光出力的技术性要求需要投入的储能成本将显著提升。

图5 储能投资成本与风-光-储联合出力标准差帕累托曲线Fig. 5 Pareto curve of energy storage investment cost and standard deviation of wind power-PV-storage joint output
3.3 敏感性分析
不同风光装机比例以及储能成本均会对储能的优化配置以及投资经济性产生影响。本文以风光比例和储能成本为影响因素,分别从储能配置变化以及投资经济性两个方面进行灵敏度分析。
(1)不同风光装机比例对储能配置的影响。
以10 MW的风电装机为标准,光伏装机容量占风电装机容量占比变化从0到1.5,风光出力波动性抑制率从10%增长到40%情况下,储能系统的配置情况如表7所示。
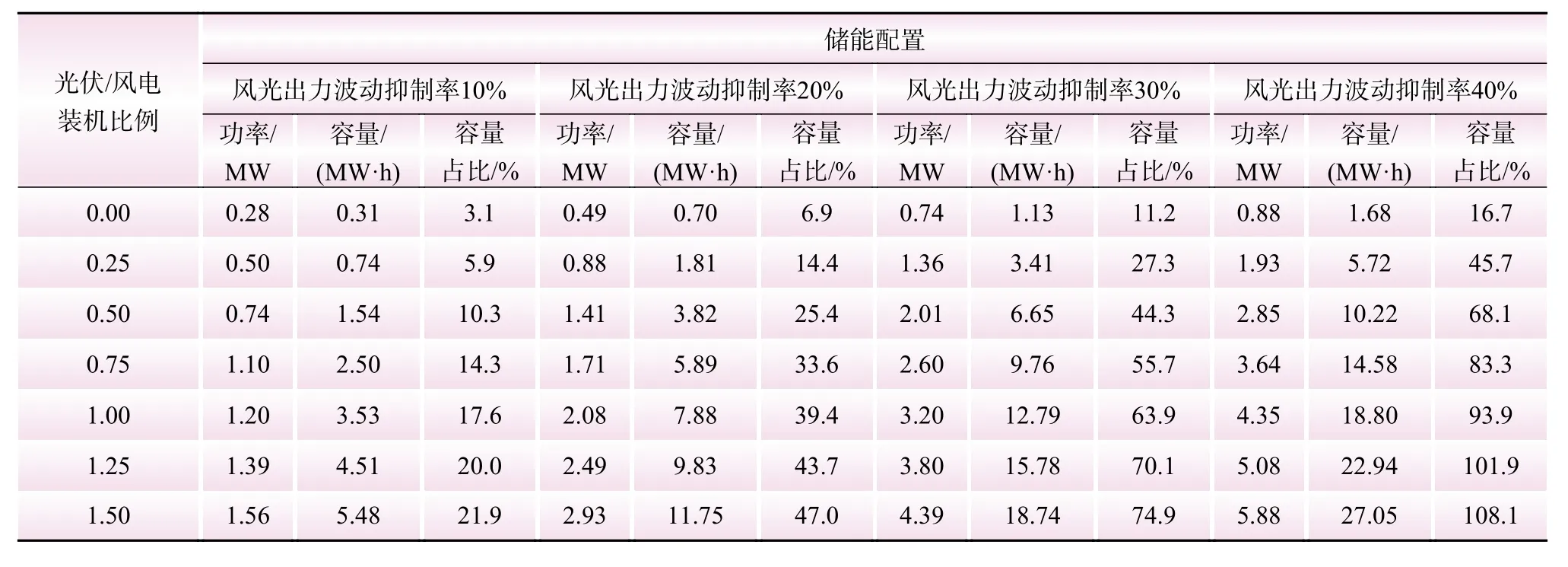
表7 不同风光比例下储能配置方案Table 7 Energy storage configuration scheme under different ratios of PV installed capacity to wind power installed capacity
为了更直观地表示不同风光装机比例对于储能配置的影响,基于表7绘制不同光伏风电装机容量比例下储能配置需求图,如图6所示。
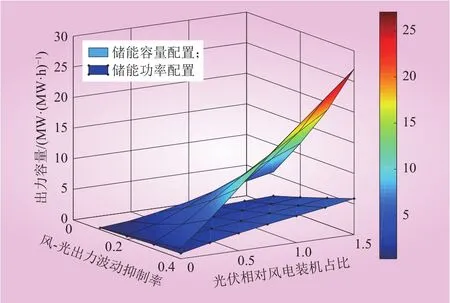
图6 不同风光比例下储能配置需求Fig. 6 Energy storage configuration requirements under different ratios of PV installed capacity to wind power installed capacity
由表7和图6可知,在风光出力波动抑制率一定的情况下,随着光伏相对风电装机占比的提升,储能容量和功率配置需求均呈现上升趋势,且容量配置需求增长趋势显著快于功率配置需求。当 σp=10%,光/风比例从0增长到1.5时,储能的功率配置需求从0.28 MW增长到1.56 MW,涨幅为457.14%,而容量配置从0.31 MW·h增长到5.48 MW·h,涨幅高达1 667.74%。在光/风比例一定的情况下,随着风光出力波动抑制率的增加,储能的容量配置需求增长趋势同样显著快于功率配置需求。当光/风比例为0.75,σp从10%增长到40%时,功率需求从1.1 MW增长到3.64 MW,涨幅为230.90%,而容量配置从2.5 MW·h增长到14.58 MW·h,涨幅高达483.2%,且储能容量占可再生能源总装机容量的比重高达83.3%。因此,较高的光/风比例以及出力波动抑制率要求下,储能的经济性配置具有极高难度。当光/风比例和出力波动抑制率分别控制在35%和30%以内时,储能的配置较为经济合理。
(2)储能成本对投资经济性的影响。
以风光出力波动抑制率为40%的情况说明储能成本变化对于经济性分析指标及技术指标的影响情况,具体结果如表8所示。其中,成本系数表示储能现有成本与原有成本的比值。

表8 不同成本系数下储能投资经济性分析Table 8 Economy analysis of energy storage investment under different cost coefficients
从表8可以看出,储能的功率配置、容量配置和现金流入对于储能的成本变化并不敏感,储能成本的下降主要影响其初始投资成本,进而影响净现值、投资回收期以及内部收益率等投资经济性指标。成本系数为1时,该项目的内部收益率仅为5%,低于设定的8%的贴现率,不具有经济性,当储能成本下降20%时,该项目的内部收益率则增长到9%,初步具有投资经性,而当储能成本下降50%时,该项目的内部收益率高达20%,具有良好的投资经济性。因此,储能成本下降是提升储能大规模配置积极性的重要影响因素。
3.4 决策指导
基于选型选址和案例分析结果,对蒙西地区进行整体优化,提出蒙西地区储能配置的规划方案。该储能配置方案的技术目标为将风光出力波动率降低30%,经济目标为实现储能的利润最大化。为了反映储能成本变化对于储能整体投资的影响,基于不同储能成本设置2个储能成本场景。情景1:储能单位容量成本为1.4元/MW·h,单位功率成本为0.35元/MW;情景2:储能单位容量成本为1元/MW·h,单位功率成本为0.35元/MW。其他参数设置与案例参数设置保持一致。不同成本场景下蒙西地区的储能配置计划如表9所示,储能配置的地址选择如图7所示。
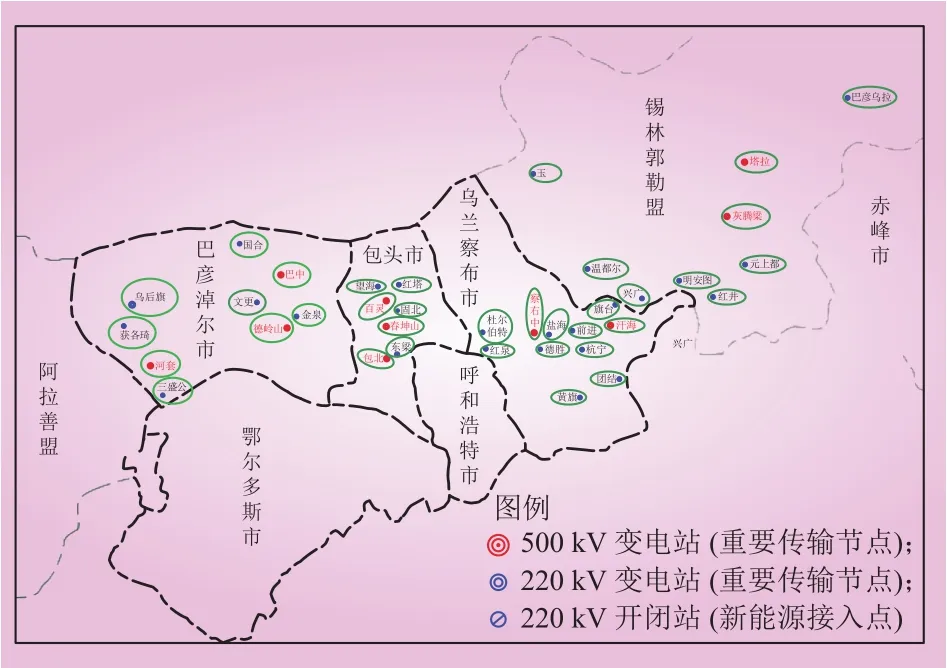
图7 蒙西地区储能选址简图Fig. 7 Simplified site selection map for energy storage in western Inner Mongolia
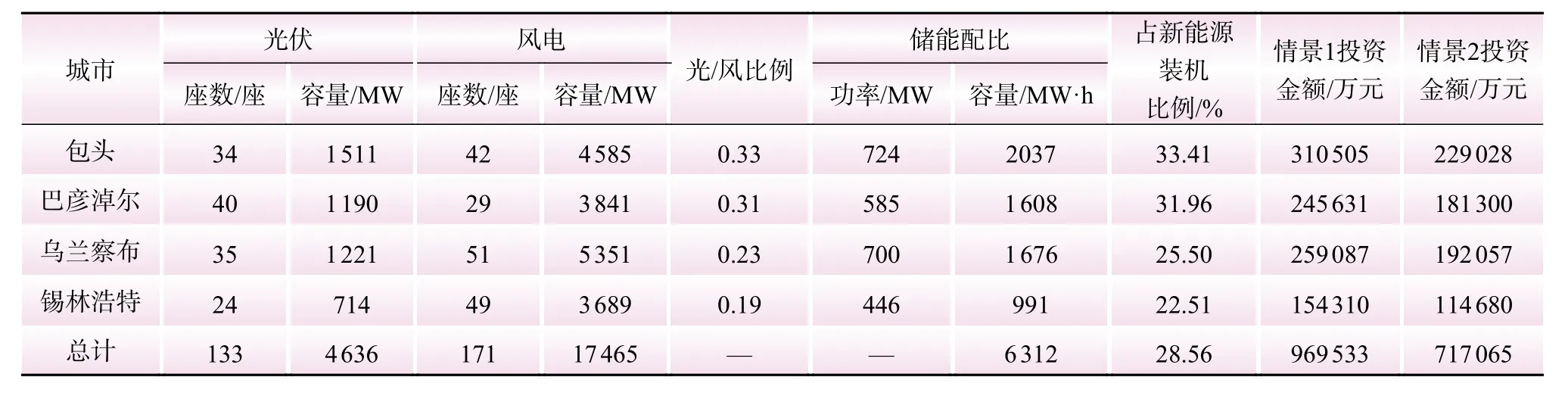
表9 不同成本场景下蒙西地区的储能配置计划Table 9 Energy storage configuration plan for western Inner Mongolia in different cost scenarios
根据《内蒙古自治区关于加快推动新型储能发展的实施意见》,配建储能规模原则上不低于新能源项目装机量的15%,本文储能配置方案中,各地区的储能配置容量均符合该政策要求。现有可再生能源装机水平下,实现降低风光出力波动性的技术要求,蒙西地区需要在情景1下投入96.95亿元建设电化学储能,而在情景2下投入71.71亿元建设电化学储能。以情景1为例,包头地区储能投资需求最高,达到31.05亿元,锡林浩特地区的储能投资需求最低,为15.43亿元。
4 结论
本文考虑储能的综合价值及其抑制风光出力波动的技术作用,提出针对蒙西地区的储能优化配置模型及具体方案。基于蒙西地区新能源实际分布及需求提出储能选址、选型方案,以最大化风光出力波动抑制率和储能项目利润为目标,构建蒙西地区储能技术经济性优化配置模型,并采用NSGA-II算法对该双目标优化模型进行求解。然后,基于蒙西某风光地区开展储能技术经济性优化配置案例分析。最后,基于选址选型结果以及案例分析结果,针对蒙西地区4大风光资源聚集区提出储能配置方案,得出主要结论如下。
(1)储能的经济性配置需要合理的风光出力波动抑制率范围,现有条件下,当风光出力波动性抑制率小于30%时储能项目具有投资可行性;(2)光伏相对风电装机的比例越大,储能配置的经济性越差,当该比例在35%以内且风光出力波动性抑制率小于30%时,储能配置具有一定投资可行性;(3)储能成本的降低不影响储能配置的技术需求,但可以有效提高储能项目的投资回报率。
对于蒙西地区储能技术经济性配置研究,可实现通过储能的经济性优化配置降低可再生能源出力波动性的目的,为地区的储能的选型、选址、功率及容量的优化配置提供决策指导,助力蒙西地区可再生能源的快速发展。

