基于多传感器数据融合的多目标跟踪算法研究

高春艳，卢 建，张明路，孙凌宇

（河北工业大学，天津 300401）

0 引言

基于多传感器数据融合的多目标跟踪是指融合多个传感器对多个目标的观测数据实现对多个目标的轨迹跟踪，以达到单一传感器和单一信号源所不能达到的测量精度[1]。对于多目标追踪的重要技术是滤波算法和数据融合算法，包括了从观测数据到目标跟踪的数据关联和对于追踪数据的保持。数据关联算法用来解决来自不同传感器的航迹是否属于同一个目标的问题，滤波在于解决传感器采集数据过程中受到噪音污染的问题。数据融合算法方面，实际应用中大多采用加权平均算法来得到融合目标位置信息，权值的分配方法对融合精度的影响很大。通常采用的方法是根据各传感器的标称精度事来确定权值[2]，并且在目标运动过程中，认定权值是固定不变的。然而，在多传感器多目标跟踪的过程中，传感器的观测偏差是不断变化的。确定每个传感器的权值大小显得尤为重要。本文研究多目标数据融合跟踪系统的设计问题，提出一种基于动态加权平均数据融合的UKF滤波多目标跟踪算法，采用分布式融合结构[3]，对于每个传感器得到的多个目标的观测信息，首先通过最近邻数据关联算法进行航迹关联，以确定传感器采集到的数据是属于哪个目标[4]；然后用无迹卡尔曼滤波完成对多目标状态估计得到目标最新的运动轨迹[5]；最后，综合多个传感器滤波轨迹，通过在每个采样周期下计算传感器的观测偏差，推导每个传感器权值大小的动态表达式，获得每个传感器的动态权值，运用改进的动态加权法融合得到最终的多目标位置估计。仿真结果表明，本文提出的算法能有效地进行航迹关联，准确地跟踪多个运动目标；与单传感器目标跟踪相比，多传感器数据融合后的目标跟踪精度得到提高。

1 问题描述

假设有m个传感器对个N目标进行跟踪，每个目标的运动方程为：

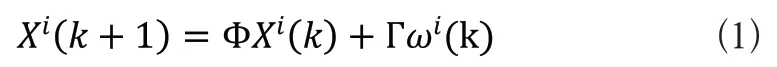
式(1)中，k表示观测时刻，i=1，2...，N，表示目标的编号，为状态驱动矩阵，为噪声驱动矩阵。表示均值为0，方差为Qi的过程噪声。第j个传感器对第i个目标观测方程为：

2 基于多传感器数据融合的多目标跟踪算法

为解决上述问题，以下将构建面基于多传感器数据融合的多目标跟踪算法。首先确定融合结构，提出基于多传感器数据融合的多目标跟踪的算法框架；接着介绍本文中中用到的数据关联算法和滤波算法，最后给出基于多目标跟踪的改进动态加权数据融合算法的实现方法，完成多目标融合跟踪系统的设计。

2.1 基于多传感器数据融合的多目标跟踪的算法框架

算法采用分布式融合结构，具体可分为以下步骤：首先，多个传感器分别探测多个目标，并获取一组观测数据，对数据进行预处理，提出背景噪声等，然后用最近邻数据关联算法完成对观测数据的数据关联，剔除虚警信息；接着采用UKF滤波完成对目标状态的估计，得到目标的运动轨迹，最后，综合多个传感器估计的目标轨迹，采用动态加权融合得到最终的轨迹。具体的算法框架如图1所示：

图1 多目标跟踪的算法流程图

2.2 最近邻（Nearest Neighbor,NN）航迹关联算法

针对每个传感器采集到的多目标数据信息，应用航迹关联算法来确定采集到定位数据属于哪个目标[6]，本文拟采用计算量小响应时间短的最近邻域法。将所有的训练样本都作为代表点，因此在分类时需要计算待识别样本x到所有训练样本的距离，结果就是与 最近邻的训练样本所属于的类别。假定有c个目标的模式识别问题，每类有标明类别的样本Ni个，i=1，2，...c。规定类1的判别函数为：

2.3 无迹卡尔曼滤波算法

目前，解决目标跟踪问题的经典滤波方法是卡尔曼滤波(KF)、扩展卡尔曼滤波(EKF)[7]或无迹卡尔曼滤波(UKF)[8]，与EKF相比，UKF算法摒弃了对非线性函数进行线性化的传统做法，采用Kalman滤波框架，使用UT变换来处理均值和协方差的非线性传递有较高的精度和较强的稳定性[9]。具体地来讲，在每一个计算周期中，UKF算法主要有以下几个关键步骤：

1）对于给定的均值和方差P，求状态一步预测以及预测误差协方差阵

（1）计算2n+1个Sigma点：

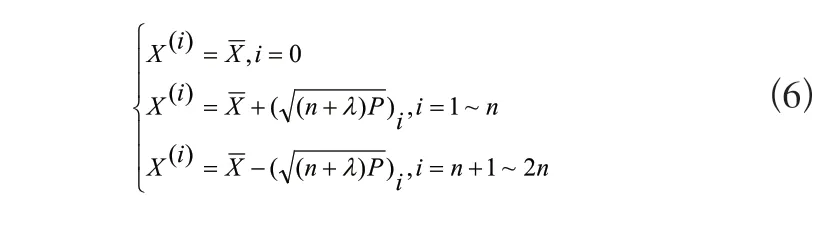
2）UT变换求Sigma点量测方程的传播

（1）由(5)式重新抽取2n+1个Sigma点

（2）计算Sigma点通过量测方程hk(.)传播后的结果进而得到量测及协方差的一步预测值。

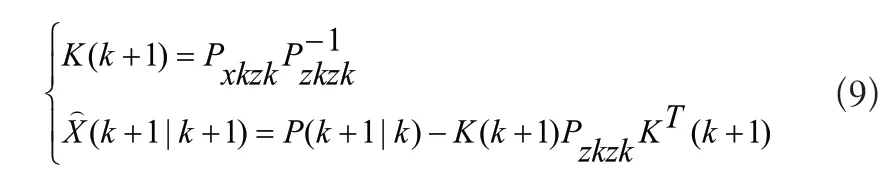
2.4 多传感器改进动态加权平均数据融合算法

在对每个传感器的数据信息进行航迹关联和UKF滤波之后，需要对相同目标的多传感器轨迹信息进行融合处理，以实现对目标的跟踪。一般的采用固定权值的加权平均法，根据各传感器的标称精度事先确定权值，精度高的传感器采用较大的权值，精度低的传感器采用较小的权重，并且在跟踪运动目标的过程中认为每个传感器的权值是恒定的[10]。但是在实际目标过程中，共有m个传感器，每个传感器的测量误差与运动过程中目标的位置有关。这里引入跟踪位置“即时误差”的概念。假定k时刻传感器n对目标α的观测位置为(x(k)，ye(k))，传感器n的k-1时刻的数据经过滤波后的对目标αk时刻的估计位置表示为那么，传感器n在k时刻对目标α的即时偏差表示为：

按照“即时偏差越小，权重越大”的原则，推导出权重传感器最优权值分配表达式为：

应用改进动态加权法的融合位置信息表达式为：

式中，Xa表示α目标的位置信息，表示i传感器对α目标观测信息的滤波值。通过上述公式，可以实现按照传感器的实时偏差对传感器赋予最优的权值，提高多传感器跟踪融合的精度。

3.仿真分析

本节将采用仿真分析的方法，通过对多目标跟踪的情景进行模拟，对本文算法的多目标跟踪性能进行检测，并将基于最动态加权数据融合的UKF滤波多目标跟踪算法融合结果偏差与单传感器偏差进行对比，以验证该算法有效性。

为了描述方便，以二维情况为例，设有两个传感器分别对三个运动目标进行跟踪。三个目标起始位置分别为（3，0），（3，80），（3，160）在x和y方向上分别以2m/s和2.1m/s的速度做匀速运动，采样周期Δt为1s，总仿真时间为30s。

过程噪声驱动矩阵为：

基于MATLAB对此系统进行仿真实验，得到两传感器分别对三个运动目标的观测、关联、滤波轨迹如图2、图3所示。其中观测数据是传感器未处理之前的原始探测数据，对它们进行最近邻算法关联处理便得到了关联轨迹，最后进行UKF滤波处理，便得到了每个传感器对三目标的滤波轨迹。

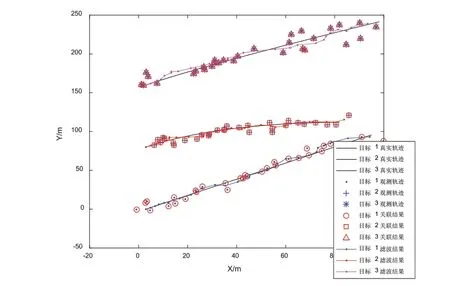
图2 传感器1对3个目标的观测、关联、滤波轨迹

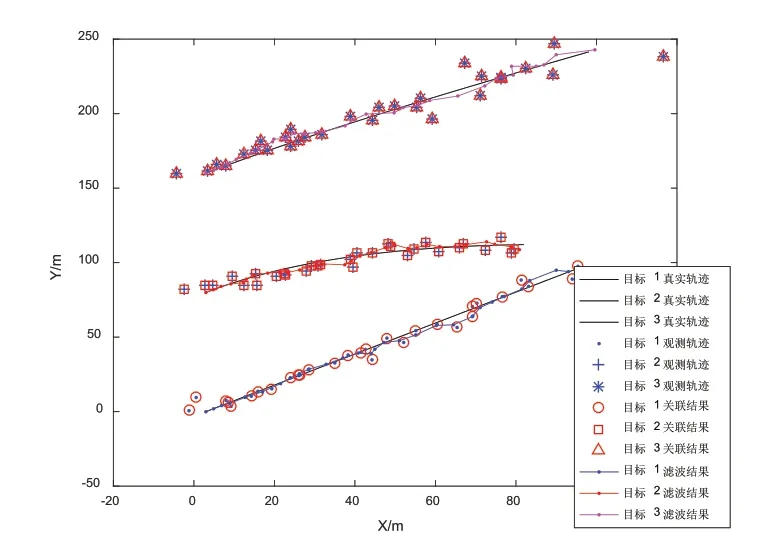
图3 传感器2对三个目标的观测、关联、滤波轨迹

三个传感器分别对两个目标进行关联、滤波的同时。对每个目标的两个传感器滤波轨迹进行动态加权融合后的得到三目标轨迹如图5所示。由图像可以看出，经过融合处理后，目标轨迹接跟真实轨迹基本重合。

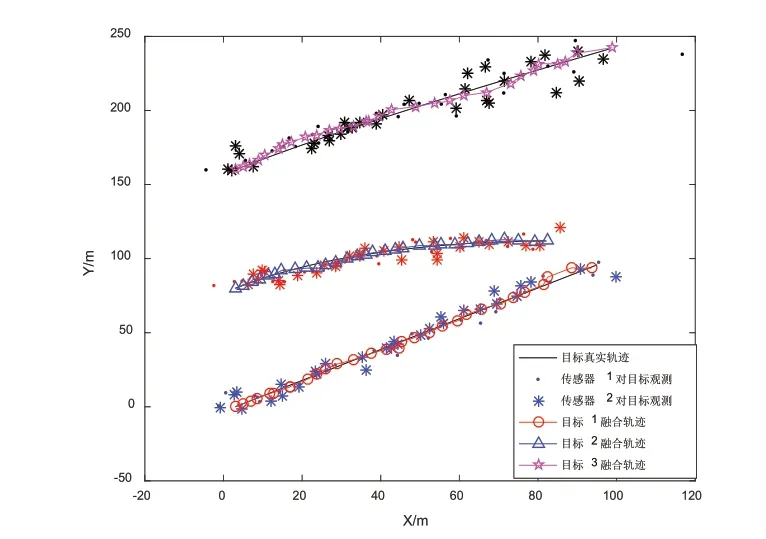
图4 融合后的目标轨迹

所谓融合偏差，是指传感器1和传感器2经过UKF滤波后，对滤波状态经过动态加权得到的融合状态，这个融合值与真实状态的偏差就是融合偏差。式(9)表示了传感器的即时偏差，那么每个传感器的整体“平均偏差”可以表示为：

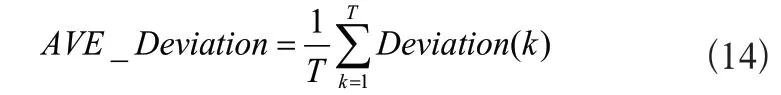
两传感器的即时偏差以及基于即时偏差的平均偏差如图5～图7所示。其中，每幅图左半边为即时偏差，右半边为平均偏差。从平均误差直方图中可以直观看出，由于动态加权融合法在每一个定位点对两个传感器的数据信息采用最优精度加权，所以得到的偏差精度比系统中任一传感器的偏差都要小。通过融合，使得目标跟踪的精度得到提高。

图5 对目标1的即时误差折线图和平均偏差直方图

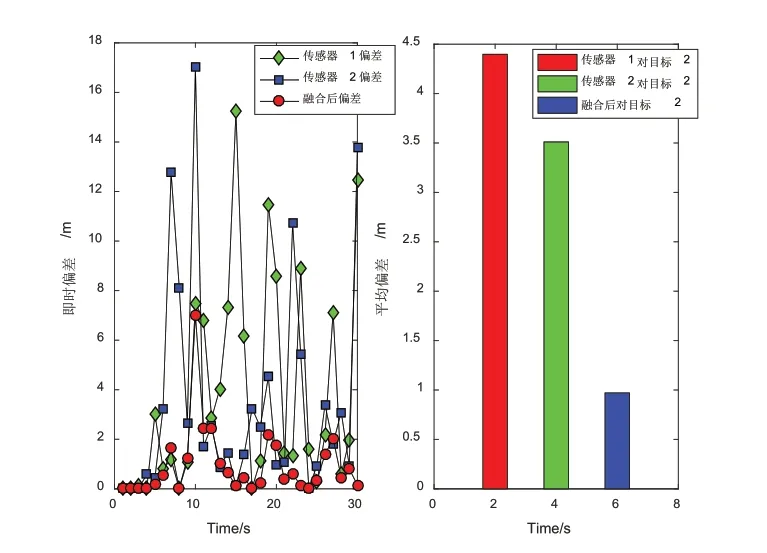
图6 对目标2的即时误差折线图和平均偏差直方图

图7 对目标3的即时误差折线图和平均偏差直方图

4 结语

针对复杂环境下多传感器多目标跟踪问题，提出一种基于改进动态加权数据融合的UKF滤波多目标跟踪算法。算法在分布式融合结构下，充分发挥了UKF算法运算速度快，精度高的优点，与最近邻数据关联算法有效结合。并且结合每个采样点的即时偏差，采用动态加权的融合方法，能够充分发挥多传感器融合的优势，增加系统的鲁棒性和实时性。实现对多运动目标的有效跟踪。结合仿真实验分析表明，提出的算法具有合理性和实用性，可为多传感器多目标跟踪提供一定的参考。