考虑设备布局的智能车间生产任务动态分配方法
丁 凯,罗 丹,张旭东
(长安大学 工程机械学院智能制造系统研究所,西安 710064)
0 引言
在智能制造环境下,智能工厂/车间内的各类制造资源拥有自感知、自配置、自控制、自决策、自学习等自治智能,各制造资源之间通过业务交互与信息共享,协作完成产品生产制造任务[1]。在此背景下,由制造资源开展动态生产任务分配(Production Task Allocation,PTA)是提高智能车间自治水平和柔性配置能力的关键。
PTA问题是根据订单交货期、成本等约束,综合考虑设备的加工能力和产能,优化安排加工任务序列的问题。PTA是车间按时完成加工任务的关键,且PTA方案需依据车间动态需求进行自适应调整。不合理的PTA将导致设备能力不均衡、生产成本提高、交货期拖延等问题。近年来,国内外学者围绕PTA问题开展了较多研究。Cheng等[2]从问题描述与建模、执行过程分析、算法设计与选择、决策优化与仿真、任务执行等角度,综述了当前PTA问题的研究进展;Li和Mo[3]提出了一种基于多属性评价的生产任务队列优化方法,根据任务属性建立了层次多属性模型,给出了指标量化方法;李益兵等[4]综合考虑生产成本、加工资源、加工效率等多个因素,建立集团分布式制造资源配置优化模型,并采用基于Logistic混沌改进的遗传算法求解该模型的Pareto最优解;Zhang等[5]建立了基于CPS和IIoT的智能生产-物流系统框架,并研究了制造资源建模和自组织配置机制;Hu和Chen[6]研究了人机协同制造系统的任务优化分配问题,并应用线性规划方法实现最佳联合系统性能;Li等[7]提出了云制造环境下资源分配模型,并针对三个优化目标提出了三种子任务调度策略;Chu 等[12]提出一种基于知识的模糊综合评价方法,解决了航空结构件生产车间的制造任务分配问题。
上述研究从不同角度开展了PTA问题的研究,但较少考虑制造资源的自主性和任务分配的动态自适应能力。本文将工件在设备之间的流转(即工序流)视为马尔科夫随机过程,提出一种改进的最大熵马尔可夫模型,并引入特征函数并进行参数训练,构建了考虑车间设备布局的生产任务动态分配模型。
1 问题建模
假设某智能车间有N台机床,包括车床、铣床和车铣复合加工中心三种类型,主要加工的工件包含H类,所有类型工件的工序总和为M个。其中:具有同种加工特征、不同加工参数的工序视为同类工序,如:粗车外圆90和粗车外圆65均为“粗车外圆”工序。智能车间生产任务动态分配问题即为:在给定的设备布局约束下,如何根据零件工艺规划流程和历史加工记录,动态设定当前工件每一道工序所在的机床,形成动态机床序列。
本文将车间设备布局视为影响条件概率的因素,改进了传统的最大熵模型结构,将智能车间生产任务动态分配问题抽象为考虑设备布局的最大熵马尔可夫模型(Layoutbased Maximum Entropy Markov Model,L_MEMM),如式(1)所示:

其中:
I——与工件加工工序对应的机床序列,为隐含状态链,I i∈Y,Y={y1,y2,...yn},Y表示智能车间拥有的机床集合。车间接到新的生产任务后,可由工件图纸生成加工工序流,但与工序流对应的机床序列是事先不可观测的;
D——机床之间的距离矩阵。D=[dij]1×N,dij表示第i号机床到第j号机床的距离;
O——工件的加工工序序列,为可见状态链,Oi∈V,V={v1,v2,...vn},V表示智能车间历史加工工件包含的所有加工工序集合;
P——满足信息熵最大约束时的三元条件概率,即:在当前工序为Ot、前一道工序所处的机床编号为It-1、由前一道工序运输到当前工序的距离最小为的条件下,当前工序Ot被分配至机床It进行加工的概率P(It|It-1,Ot,Dt)。
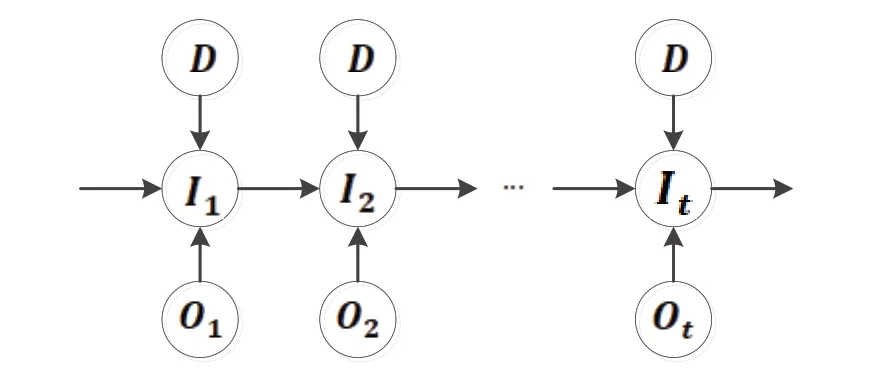
图1 考虑设备布局的最大熵马尔科夫模型
L_MEMM模型中最终得到的指数分布Pyi-1(y1IxI),在引入物流距离D之后变量x和y有了新的含义,变量x表示工件的加工工序序列,变量y表示在时间上与工序对应的工件所处的机床序列,则条件概率分布P可由以下公式计算:

矩阵中Pij表示工件的第一道工序为vi且该工序所处的机床为yj的概率。
考虑设备布局的智能车间生产任务分配问题对工件当前工序、前一道工序所处机床以及当前工序所处的机床等信息非常敏感,需要将传统的MEMM模型中的原始特征函数重新定义如式(5)所示:
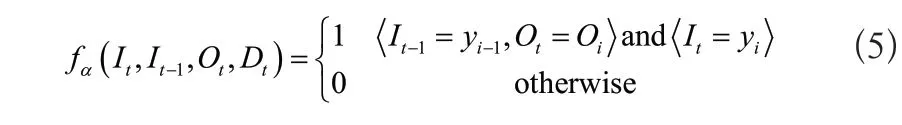
特征函数定义为一个二值函数,这种特征能够捕获特定工序在满足特征函数的条件下工件所处机床的倾向,如果上述定义中特征fα(.)对应的权重ωα为较大正值,就表示在满足特征函数的条件下,当前工序oi有较大概率在机床yi上加工,则最佳的物流路径即为上一道工序所在机床yi-1到当前工序所在的机床yi。
2 算法求解
2.1 模型训练
采用迭代尺度算法对模型进行训练,具体步骤如下:

3)计算每个特征函数的样本期望Eα:

4)迭代计算:

5)设置迭代结束条件:
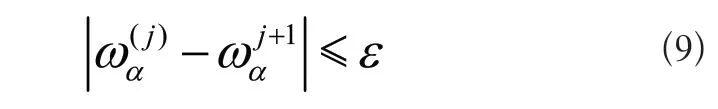
若满足条件5),结束迭代并输出权重ωα(α=1,2...,m),否则返回步骤2)。
训练结束后得到每个特征对应的权重,代入最大熵模型的解即可获得满足约束条件的条件概率分布P(It|It-1,Ot)。
2.2 生产任务分配预测
以工件加工工序序列为输入,采用Viterbi算法对工序序列对应的机床序列进行预测。生产任务动态分配问题本质上是一个动态规划求概率最大路径问题,一条物流路径与一条机床序列相对应。本文建立的模型为概率模型,根据动态规划原理,最优的路径具有以下特性:如果工件在t时刻通过机床那么这一方案中从机床到终点机床的部分序列,对于从的所有可能的部分序列来说是最优的。
定义变量δ、ψ,定义工件进行到第t道工序时处于机床i的所有可能的方案i1,i2,...it中最有可能出现的机床序列,其概率由式(10)计算:

由定义可得δ的递推公式如式(11)所示:
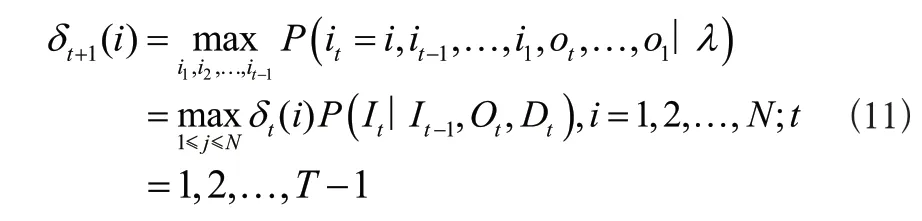
定义工件加工进行到第t道工序时处于机床i的所有可能的分配方案(i1,i2,...,it-1,i)中,最有可能出现的机床序列,其第t-1个机床由式(12)计算得到:

从第一道工序t=1开始,递推计算在第t道工序工件处于机床i的各分配方案部分序列的最大概率,直至得到最后一道工序t=T时工件处于机床i的所有可能方案的最大概率,最后一道工序t=T的最大概率即为最佳的生产任务分配方案出现的概率P*,最优方案的终点机床也同时得到,从终点机床开始,由后向前逐步求得前一道工序所处的机床最终得到与工序序列相匹配的最大概率的生产任务分配方案
3 案例研究
某智能车间共有8台机床,其中:a、b为普通车床,c为数控车床,d、e、f为数控铣床,g、h为车铣复合加工中心,各机床之间的物流距离矩阵D如式(13)所示:

该车间当前待加工工件包括传动轴、法兰端盖、法兰盘和阀盖。为便于表达,将各工件的加工工序编码如表1所示。

表1 加工特征编号
将工件加工工序进行编码,形成四类工件的加工工序序列O:

将由车间历史数据构成的训练集数据输入到模型训练算法中,模型包含的特征由训练数据直接提取,特征格式如式(14)所示。
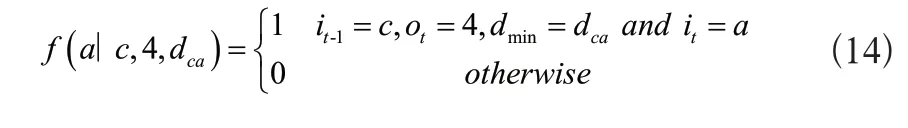
式(14)表示前一道工序在机床c上加工,当前工序为精车外圆,在除机床c外的所有机床中,机床a与机床c的物流距离最短,且当前工序在机床a上进行加工。扫描训练集后得到上述形式的特征函数72个,每个特征对应权重的训练结果如图2所示。

图2 算法训练权重结果

由于矩阵规模较大,本文只给出部分结果如式(16)所示
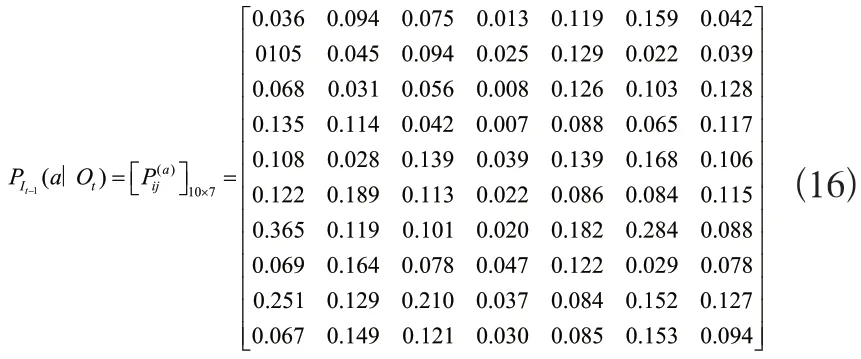
将得到的模型最优参数与预测目标序列O代入Viterbi算法,计算后得到与四类工件的加工工序序列相对应的四条机床序列如式(17)所示:
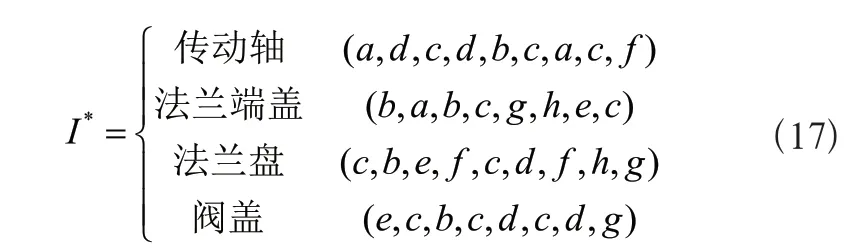
4 讨论分析
以传动轴为例对预测结果进行分析,L_MEMM模型预测得到的结果为:a→d→c→d→b→c→a→c→f,而根据车间内各类机床的加工能力和物理布局得出的理论最优的物流路径为:a→d→b→d→b→c→a→c→f。通过对比发现,只有第三道工序对应的预测结果与理论结果之间存在偏差,但是普通车床b与数控车床c都能满足第三道工序车削端面,而数控车床c与上一道工序所在的机床d之间的物流距离最短,故预测结果可靠。
进一步地,本文以平均绝对误差(Mean Absolute Error,MAE)及均方根误差(Root Mean Square Error,RMSE)作为预测结果准确率的评价指标:
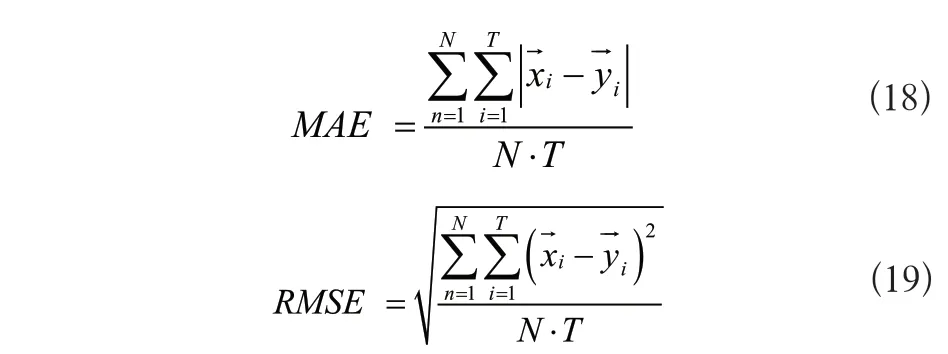
式中:N表示实验次数,表示实际的机床序列,表示预测得到的机床序列,T表示工件加工工序数量。因此,MAE和RMSE描述的是对于同一工件的加工工序序列,模型预测得到的机床序列与实际机床序列的偏差度量,其数值越小说明预测结果越准确。
本文给出L_MEMM与传统的隐马尔可夫模型(Hidden Markov Model,HMM)之间的预测结果对比如表2和表3示所示。
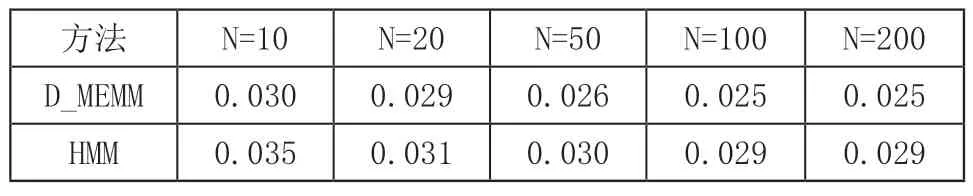
表2 MAE值对比(T=10)

表3 RMSE值对比(T=10)
由实验结果可知,随着工序数量的增加,L_MEMM模型预测准确性更好,原因是L_MEMM以一个条件概率分布替换了HMM的状态转移概率分布和观测概率分布,更符合智能车间生产任务动态分配的实际情况。
5 结语
本文研究了一种考虑设备布局的最大熵马尔科夫模型来解决智能车间生产任务动态分配问题。该方法依据历史生产任务数据进行特征自提取,在遵循最大 模型框架下进行模型训练。案例表明,该方法改进了HMM模型的固有缺陷,为智能车间制造任务动态分配预测提供了方法。由于智能车间生产执行过程是一个相当复杂的过程,后续工作需要进一步考虑车间实时生产环境数据等在生产任务动态分配中的影响。

