格构式超高墩力学分析与施工监控

程献访, 曹 晗, 蒋 志, 牛忠荣, 胡宗军

(1.合肥工业大学 土木与水利工程学院,安徽 合肥 230009; 2.中铁四局集团钢结构建筑有限公司,安徽 合肥 230022)

连续钢桁梁桥结构技术成熟,其竖向和横向刚度大且具有较强的跨越能力,被广泛应用于我国的铁路桥梁建设。大跨度连续钢桁梁桥通常采用悬臂拼装法架设,为减小施工过程中桥梁的最大悬臂架设长度,提高其抗倾覆能力,需要在跨间布置临时支架或临时墩,以控制体系转换前钢桁梁桥支座处的最大负弯矩,防止施工过程中桥梁发生倾覆。在山岭重丘区、深沟峡谷等复杂地形下,辅助结构临时墩的高度很大。桥梁悬臂架设期间,超高墩的稳定性与承载性能直接影响上部桥梁的施工[1]。因此,对超高墩在桥梁悬臂架设中的受力状态进行研究是必要的,也需要在施工中实时监控其应力和位移状态[2-5]。目前,国内关于钢桁梁桥力学模拟与施工监控的研究成果较丰富。文献[6]针对钢桁梁桥半悬臂半简支状态,提出钢桁梁前端挠度与墩顶反力呈线性关系;文献[7]对比分析格构式风电塔架腹杆和塔柱节点刚接、铰接及半刚性连接3种模型计算结果的区别;文献[8]研究临时墩的设置和可变载荷对三塔式组合梁斜拉桥结构稳定性的影响;文献[9]对大跨度简支梁桥双悬臂架设进行力学分析。

本文以新建玉溪—磨憨铁路元江双线特大桥为例,对连续钢桁梁桥悬臂拼装施工过程中格构式超高墩结构进行力学分析,建立钢桁梁和超高墩力学模型,并根据计算结果设计现场施工监控方案;通过对比有限元法计算值与现场监控数据,分析超高墩结构承载性能,以保障桥梁施工过程中超高墩结构的安全与稳定。

1 工程概况

元江双线特大桥为5跨连续钢桁梁桥,跨径为(108.0+151.5+249.0+151.5+108.0) m,钢桁梁全长768.0 m。桥梁及辅助工程立面布置如图1所示(单位为m)。

图1 桥梁及辅助结构立面布置

该桥结构为下弦曲线变化的变桁高上承式钢桥,由左右2片主桁组成,主桁中心距16.0 m,钢桁梁平弦段腹杆为N型结构,变高段腹杆为K型结构。主墩左右两侧各2个节间长15.0 m,其余节间长13.5 m,全桥共56个节间。平弦段桁高16.0 m,变高段桁高由16.0 m渐变至36.0 m。桥梁主结构用钢量约20 000 t。钢桁梁施工方案为双向对称悬臂架设,在跨中合龙。为保证桥梁在施工过程中的安全,减小钢桁梁的悬臂拼装长度,施工期间需在两岸边跨和次边跨设置临时拼装支架和2座钢结构超高墩L5和L6。钢桁梁架设过超高墩悬拼5个节间至主墩后,在主墩起顶落梁,超高墩脱空。

两岸超高墩L5、L6对称布置,距边墩81.0 m,高度分别为110.9、133.1 m,结构为12根钢立柱格构式变刚度支架,平面尺寸由墩底21 m×12 m变化为墩顶21 m×6 m。超高墩主要承重结构钢立柱每节8 m或9 m,节段之间焊接。立柱之间设置联结系和平面桁架,连接方式为螺栓连接。每榀柱顶设置3层箱型截面分配梁,分配梁接触位置四周满焊,总高度为4.5 m。超高墩基础采用人工挖孔灌注桩,墩身结构杆件均采用圆钢管,材质均为Q345B,许用应力为295 MPa。本文以超高墩L6为例,介绍超高墩结构力学分析模型的建立与施工监控结果。超高墩L6结构如图2所示(单位为m)。

图2 超高墩L6结构

2 钢桁梁桥悬臂施工过程力学分析

2.1 钢桁梁桥悬臂架设的力学模型

两岸超高墩L5和L6是钢桁梁悬臂架设施工中重要的大型临时结构,钢桁梁架设从超高墩向跨中悬拼5个节间至主墩期间,超高墩与桥台、边墩共同承担上部桥梁荷载,在主墩顶起钢桁梁并安装临时支座后,超高墩脱离工作。根据钢桁梁桥悬臂施工方案,分别建立钢桁梁桥与超高墩施工过程的力学模型。力学模型合理简化结构连接螺栓、节点板等结构,将钢桁梁桥的钢材密度放大1.25倍,边跨和次边跨钢桁梁实际质量为6 646 t;将超高墩L6的钢材密度放大1.27倍,实际质量为1 140 t。钢桁梁桥悬臂拼装杆系有限元法分析模型如图3所示。

根据桥梁悬臂拼装期间桥支座实际状态,按照杆系结构,有限元模型中桥台和边墩处边界条件为简支约束,桥台上游支座约束横桥向(y方向)和竖向(z方向),下游支座约束竖向(z方向);边墩上游支座约束x、y、z方向,下游约束x、z方向。架梁吊机自重荷载施加在当前拼装节间后第1节间的上弦杆4个节点处。

图3 钢桁梁桥悬臂拼装有限元法模型

超高墩结构有限元模型所有杆件均为梁单元,节点之间刚接,边界条件为：超高墩下部12根钢立柱柱脚全部固结,墩顶3层分配梁之间刚性连接。

钢桁梁与超高墩计算模型中荷载组合考虑结构自重、质量为186 t的吊机荷载、施工活载、风荷载和温度荷载。① 施工活载,根据文献[10]取值为1 kN/m2;② 温度荷载,根据当地全年气候条件,考虑升温30 ℃与降温25 ℃的温度荷载;③ 风荷载,按照文献[10],垂直于超高墩表面上的水平风荷载标准值wk计算公式为:

wk=βzμsμzw0

(1)

其中:wk为风荷载标准值;βz为高度z处的风振系数;μs为风荷载体型系数;μz为风压高度变化系数;w0为基本风压,取值为0.4 kN/m2(风速相当于25 m/s)。

施工过程计算荷载考虑结构自重、施工活载、风荷载和温度荷载。当钢桁梁悬臂架设至超高墩上方,通过有限元法计算可得:钢桁梁下弦杆E14节点(上、下游各1个)竖向挠度为-368 mm,顺桥向位移为24 mm,横桥向位移为5 mm。为减小最大悬臂工况下超高墩所承担的荷载,施工方案为:维持钢桁梁原有竖向挠度不变,钢桁梁E14节点与超高墩L6支点之间用钢垫板垫实,在垫板四周焊接限位板,超高墩由组立状态转为工作状态,开始承受上部钢桁梁传递的载荷。钢桁梁E14节点与超高墩L6墩顶分配梁接触示意如图4所示。

钢结构超高墩水平和竖向刚度与通常的混凝土结构墩相比较小,在可变荷载和钢桁梁悬臂变长度拼装荷载作用下,超高墩与钢桁梁之间为复杂接触关系。因此,需要将钢桁梁与超高墩作为一个整体结构,模拟施工过程的力学行为,获得钢桁梁对超高墩的作用力。

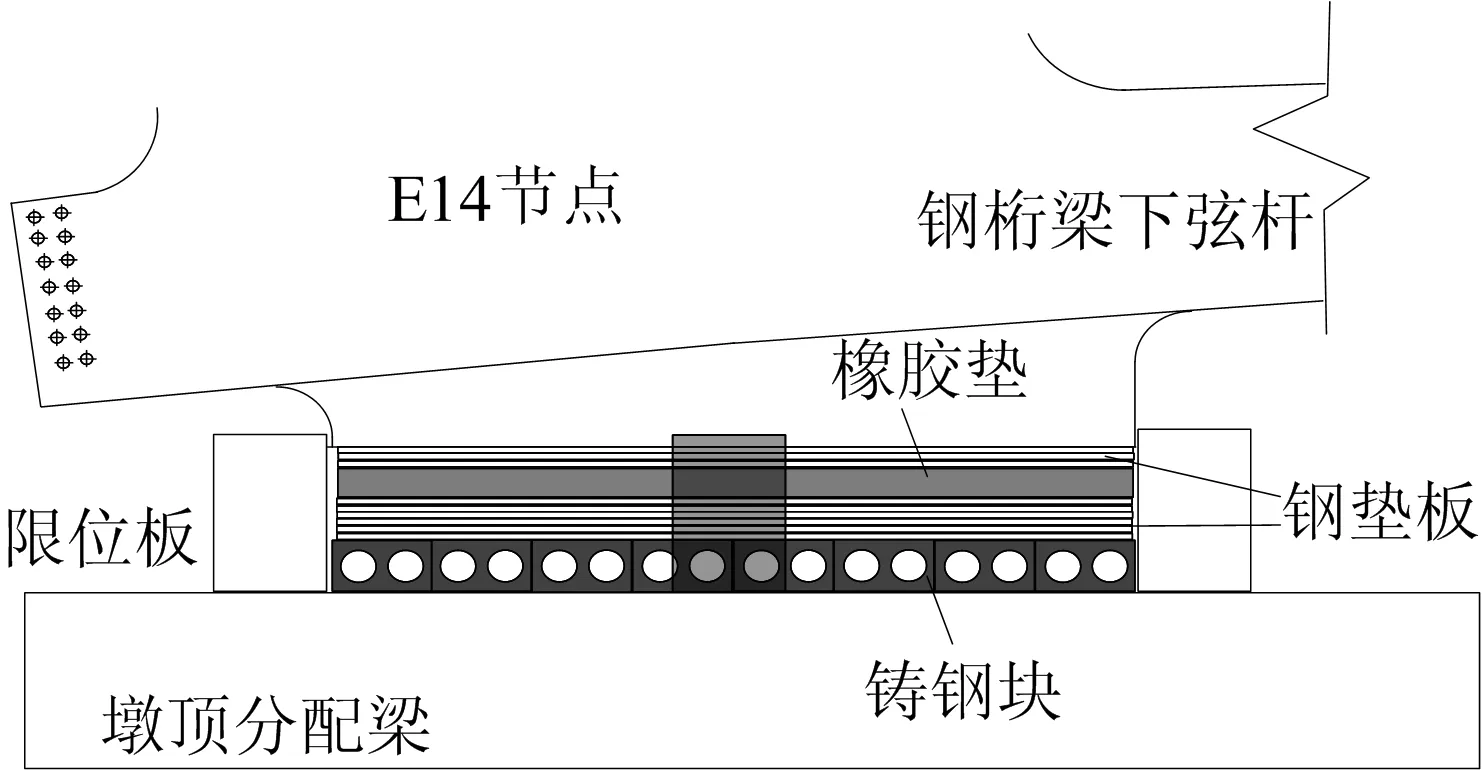
图4 钢桁梁E14节点与超高墩L6墩顶分配梁接触示意

由于钢桁梁架设越过超高墩以后的悬臂长度陆续增长,钢桁梁与超高墩结构接触位置各方向自由度的弹性刚度不能确定,难以用传统方法模拟两者之间的接触行为。钢桁梁在施工过程中竖向挠度为主要变形,根据线弹性结构叠加原理,在小变形条件下,梁的挠度、转角与荷载成线性关系[11]。因此,合理简化钢桁梁与超高墩接触位置的边界条件,通过在钢桁梁上、下游2个E14节点施加于超高墩2个竖向集中力,其反作用力FR为超高墩对钢桁梁的竖向支承力。支承力FR大小与钢桁梁悬拼各工况下的支承状态——E14节点的竖向挠度w有关。超高墩与钢桁梁E14节点接触关系可按照半悬臂半简支状态下建立[6](钢桁梁E14节点有竖向挠度w,非完全简支),FR与w关系为:

FR=kw+FR0

(2)

其中:k为钢桁梁E14节点处竖向弹性刚度;FR0为钢桁梁E14节点完全简支状态下(即钢桁梁呈水平状态),超高墩对E14节点竖向支承力。

根据 (2) 式,通过w,可以求得桥梁悬拼各工况下FR,从而建立起悬臂拼装时钢桁梁与超高墩的荷载联系。

2.2 钢桁梁悬臂架设过程超高墩力学分析

钢桁梁架设过超高墩悬拼5个节间后至主墩,利用有限元法模拟钢桁梁悬臂架设施工过程,计算分析超高墩组立完成(超高墩组装完成、未工作状态)与钢桁梁悬拼工况下的承载性能。超高墩主要计算工况为:① 超高墩组立完成;② 工况0,钢桁梁落梁到超高墩(初始状态);③ 工况1～工况5,钢桁梁越过超高墩分别悬拼第1节间至第5节间完整节间状态。计算荷载包括结构自重、施工活载、架梁吊车自重、风荷载、温度载荷。

2.2.1 竖向支承力FR计算结果

本工程钢桁梁悬臂拼装施工过程符合变结构线弹性力学模型,根据有限元法和(2)式计算得到不同工况下w与FR的关系。k值计算方法如下:以钢桁梁架设至超高墩上方时工况0为例,通过有限元计算确定钢桁梁完全简支(钢桁梁呈水平状态),即w=0 mm时,FR0=4 370 kN;钢桁梁完全悬臂(E14节点无支承力),即FR=0 kN时,w=-368 mm,根据 (2) 式可确定k值,其余工况类似。钢桁梁架设各工况下w与FR的关系如图5所示,可见各工况下k值几乎不变。

图5 各工况下E14节点挠度w与竖向支承力FR关系

钢桁梁架设至超高墩上方时,现场实测悬臂端E14节点竖向挠度为-246 mm,与计算值-368 mm不同,原因是模型中计算荷载与现场施工有一定的偏差,导致计算值偏大。本文根据现场实测,取w=w实际=-246 mm,由 (2) 式计算求得钢桁梁实际施工中,各工况下超高墩每榀柱顶对钢桁梁的单点竖向支承力F实际,结果见表1所列。

表1 k值与E14节点单点竖向支承力F实际计算结果

表1中,钢桁梁完全简支状态(钢桁梁呈水平状态),各工况下墩桥之间单点相互作用力FR0也一并列出。工况0为上超高墩工况,因钢桁梁上架梁吊机位于超高墩左侧(见图3),超高墩工作状态下各工况E14节点的实际挠度一直为w=w实际=-246 mm,故k值稍小于工况1～工况5。工况5为钢桁梁最大悬臂拼装状态,超高墩对钢桁梁E14节点的作用反力F实际为21 613.2 kN。钢桁梁由左右2榀对称桁梁组成,超高墩L6通过上、下游2个E14节点对钢桁梁提供支承力,故超高墩L6受到的钢桁梁作用力为2F实际。

2.2.2 组立完成工况超高墩计算结果

两岸超高墩L5、L6高度分别为110.9、133.1 m,属于高耸钢结构,且水平横桥向刚度大于顺桥向刚度,组立完成后受到顺桥向风荷载影响较大。组立完成工况超高墩L6在自重、温升30 ℃和顺桥向风荷载作用下,有限元法计算结果如下:

(1) 超高墩柱脚应力和墩顶顺桥向位移最大。

(2) 最大组合应力为-193 MPa,位于靠山侧上、下游柱脚(测点12、测点9);斜腹杆最大组合应力为-101 MPa,位于靠山侧下游(测点13);超高墩结构应力小于Q345B钢材的许用应力295 MPa。

(3) 墩顶最大顺桥向位移为288 mm(组合位移为290 mm),偏向靠山侧。

根据文献[12]规定,在风荷载或多遇地震作用下,塔楼处的剪切位移角θ不宜大于1/300。超高墩L6墩顶顺桥向变形为290/133 100<1/300,满足文献[12]要求,超高墩处于安全状态。

有限元法计算的超高墩L6组合应力和组合位移云图如图6所示。

结果以“平均值±标准差”表示，数据处理与分析采用SPSS 16.0统计软件进行方差分析和差异显著性比较，以P＜0.05作为差异显著性判断标准。

超高墩L5的结果与L6类似。

图6 超高敦L6组立完成最大组合应力和位移云图

2.2.3 悬臂架设各工况下超高墩计算结果

钢桁梁过超高墩L6悬拼第5节间后至主墩,最大悬臂长度为70.5 m。悬拼节间桁高由16.0 m渐变至36.0 m;钢桁梁第1节间质量最小,为356.1 t;第5节间质量最大,为716.9 t。随着施工进行,超高墩底部支反力呈凹曲线增长,工况5下超高墩最大支反力为54 360 kN。钢桁梁过L6墩悬拼5个节间期间,地面对L6墩支反力计算值如图7所示。

图7 悬拼5个节间期间超高墩L6底部支反力计算值

钢桁梁悬臂架设工况5悬臂最大,超高墩承受的单点竖向集中力FR′(超高墩对钢桁梁竖向支承力FR的反作用力)达到最大,为21 613.2 kN,为最危险工况,共有2个着力点,故超高墩受到钢桁梁的作用力为43 226.4 kN。通过有限元法计算分析,在温升30 ℃和顺桥向风荷载作用下,超高墩L6在工况5下的组合应力和组合位移分布如图8所示。

图8 超高墩L6在工况5下最大组合应力和位移云图

由图8可知：

(1) 最大组合应力为-246 MPa,位于靠山侧下游柱脚(测点9);12根超高墩柱脚中,靠山侧4根柱脚组合应力均大于230 MPa,中间层和靠河侧柱脚应力依次减小。

(2) 斜腹杆最大组合应力为-117.5 MPa,位于靠山侧下游(测点13)。

(3) 超高墩刚度变化拐点处最大组合应力为-146.2 MPa,焊缝上下钢立柱应力变化平稳。

(5) 墩顶最大顺桥向位移为262 mm(组合位移为264 mm),小于超高墩组立完成工况下位移,剪切变形满足文献[12]要求。

超高墩L6工况5和组立工况下最大组合应力和位移发生处位置相同,结构应力均小于Q345B钢材的许用应力295 MPa,结构处于安全状态。

3 超高墩施工过程应力和变形监控

3.1 超高墩应力和变形监控测点布置

超高墩主要承重杆件为12根钢立柱,钢桁梁过超高墩悬臂拼装5个节间至主墩过程中,各工况下超高墩承受的荷载差距很大,施工监控采用应力传感器实时跟踪监测超高墩结构应力和位移状态,发生数据异常时,及时报警查找原因,排除施工风险。根据有限元计算结果,在超高墩应力较大部位和结构尺寸变化处安装钢弦式应变计,共24处。在柱脚和墩顶粘贴反光片,监测超高墩基础沉降和墩顶位移。超高墩应力、位移测点编号如图9所示(应力测点编号由下游到上游顺序排列)。

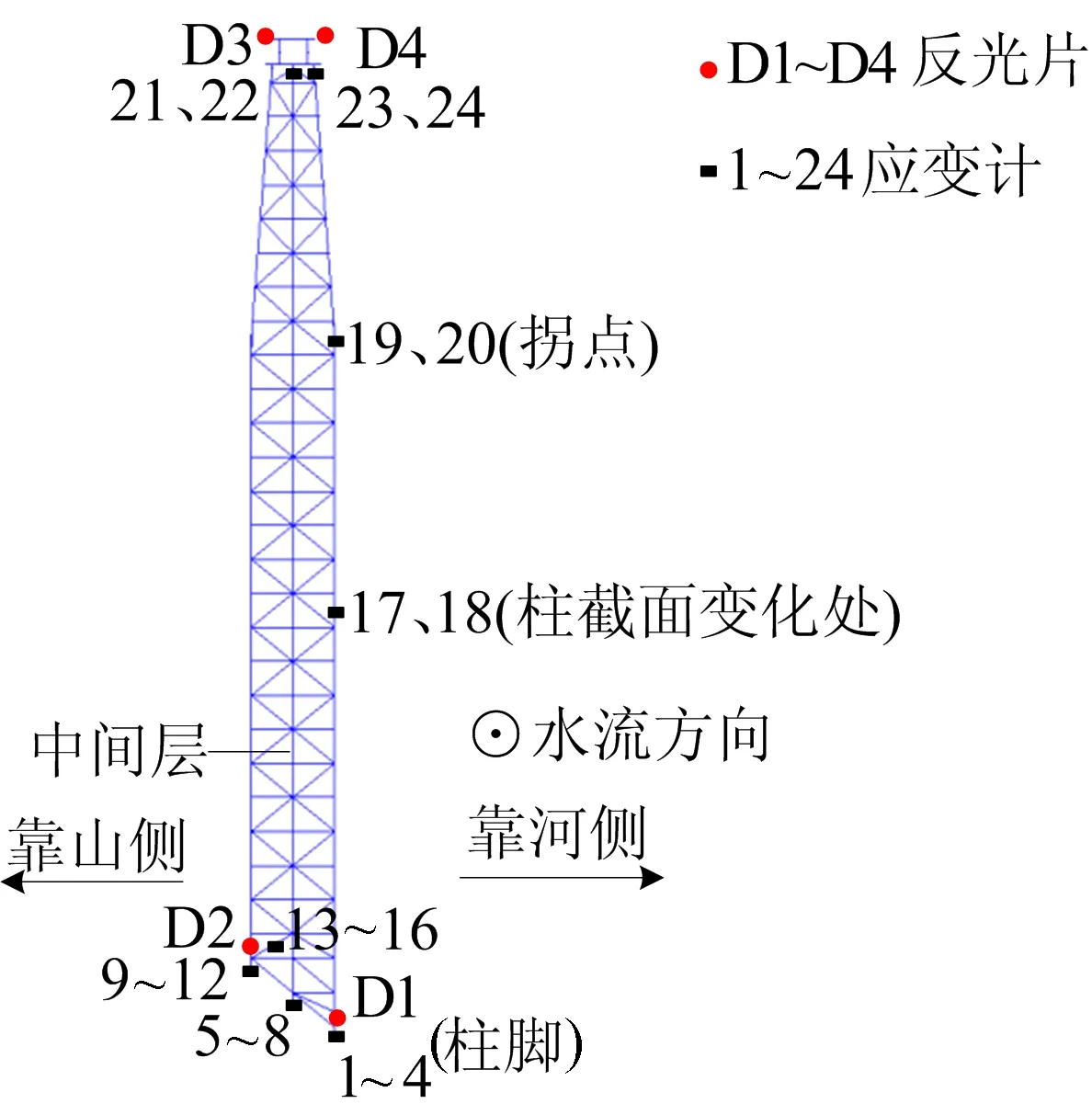
图9 超高墩应力、位移测点布置

3.2 超高墩应力和位移监测结果

3.2.1 应力监测结果分析

从超高墩L6应力测量数据中选取工况3～工况5下超高墩柱脚、柱中刚度变化拐点与柱顶3个不同位置处测量值与计算值进行对比。

(1) 钢桁梁悬臂架设工况下,靠河侧柱脚测点3、靠山侧柱脚测点11、超高墩拐点处测点20、靠河侧柱顶测点24、中间层柱顶测点22实测应力与计算值对比见表2所列。柱顶(测点24、测点22)应力实测值和计算值较为接近,误差在15%以内;柱脚与拐点处(测点3、测点11、测点20)应力实测值与计算值相差较大,原因是超高墩柱脚和拐点处应力受弯矩影响较大,而轴向应变计只能测量粘贴位置处沿杆件轴向应力。

(2) 工况5为钢桁梁悬拼至主墩第5节间,为安全考虑,现场施工流程为:架梁吊机移动到第4节间准备吊装第5节间杆件,首先安装第5节间下弦杆,杆件定位初拧高强螺栓后,最远端E19节点(节点位置见图3)在主墩用钢板垫实,然后继续安装剩下的杆件。因此,钢桁梁吊装第5节间期间,该节间已不是完全悬臂状态,导致计算值与实测值有较大差别。

(3) 钢桁梁悬臂架设各工况下,超高墩中间层柱顶测点22、中间层柱脚测点5应力测量结果与有限元计算值对比如图10所示,应力测量值与组合应力计算值差距很小。

(4) 钢桁梁悬臂架设期间超高墩拐点处实测应力数据变化平稳,钢立柱之间焊缝良好;整个施工期间超高墩最大应力出现在工况5下测点24处,为-87.2 MPa,计算应力为-96.9 MPa,均小于Q345B的许用应力295 MPa,超高墩结构处于安全状态。

表2 工况3～工况5实测应力与计算值对比 单位:MPa

图10 各工况下超高墩L6柱顶、柱脚应力变化实测值与计算值对比

3.2.2 位移监测结果分析

钢桁梁最大悬臂工况5下,超高墩墩顶D3、D4位移测点处,最大顺桥向位移为35 mm,最大横桥向位移为14 mm,最大竖向位移为42 mm(对应的位移计算值分别为30、4、58 mm),根据文献[12],超高墩剪切位移角θ小于1/300,满足安全施工要求。

4 结 论

本文针对新建铁路元江双线连续钢桁梁桥悬臂架设施工建立力学模型,采用有限元法对钢结构超高墩进行数值分析,并对其施工过程的应力和变形进行监控,得出以下结论:

(1) 针对超高墩,根据现场实际合理简化墩桥之间接触条件,建立墩-桥相互作用力学模型,经过施工过程应力监测数据验证,该简化方法合理可靠。超高墩组立施工期间和钢桁梁悬臂拼装各工况下,实时监测施工过程中超高墩结构应力和位移状态,应力监测结果与有限元计算结果较为吻合,验证了本文对钢桁梁和超高墩的力学分析结果,建立的应力监控体系保证了桥梁的安全施工。

(2) 超高墩在组立工况下,风荷载和温度效应的影响较工作期间更大,针对该施工过程的有限元分析是必要的。超高墩组立施工期间遇到大风恶劣天气应停止施工,应力监控工作应持续到超高墩脱离工作(即拆除后)为止。