分布式电源系统启动稳定性研究

马 宁，韩 冬，孙 勇

分布式电源系统启动稳定性研究

马 宁，韩 冬，孙 勇

（南京电子技术研究所，江苏南京，210039）

分布式电源系统在启动时，会面临级联电路带来的母线电压振荡及异常工作电压等稳定性问题，因此需要进行针对性设计和改进。本文针对两级Buck电路级联电源系统，基于功率守恒原理建立大信号系统模型，直观地分析了系统启动过程中各个模块软启动工作原理及出现关断重启现象的原因，并推导出级联电源系统启动稳定性的关键参数公式。接着对系统进行行为级建模仿真，在满足电路性能需求的基础上，验证了通过合理设置两级电源输出电容、负载电源启动点、系统软启动时间等以符合启动稳定性参数公式，可保证分布式电源系统的启动稳定性。

分布式级联电源系统 启动稳定性 行为级仿真

0 引言

随着电子信息装备朝多功能一体化、轻薄化和低成本的趋势发展，对装备供电系统提出了新的要求。与传统的集中式电源系统（Centralized Power System，CPS）相比，分布式供电系统（Distributed Power System，DPS）采用多个变换器组成并联、级联结构，具有系统架构灵活、动态特性好、可靠性高、适应模块化结构要求且便于维护等优点，广泛应用于通讯、舰船、航空供电系统和新能源发电领域[1-5]。

然而，直流分布式电源系统中电源级联所造成的稳定性问题成为电源系统设计的难点。由于系统子模块间复杂的相互作用，级联电源在启动或动态负载等大信号扰动情况下，出现系统振荡或输出电压异常，从而影响供电稳定性，导致负载异常工作[6-8]。因此需要在设计初期即对可能出现的稳定性问题进行针对性的设计和改进[9,10]。

现有对级联型电源系统稳定性研究大多依据小信号分析方法，采用奈奎斯特稳定判据、劳斯判据、波特图等经典控制理论[11-15]。小信号分析方法适用于研究处于稳态工作点附近的稳定性情况，在级联电源系统中，小信号的稳定并不能保证系统在启动过程和存在负载动态等大信号扰动下的稳定性[16]。

级联系统的大信号稳定性分析主要包括数字化仿真和解析法[17-19]。相较于成熟的小信号分析方法，大信号稳定性分析在一定程度上缺乏系统性理论成果。目前其主流的分析方法侧重于仿真研究，难以在实际工程中对电源模块或电源系统参数提供理论指导。

本文基于功率守恒原理建立大信号系统模型，着重从工程角度直观地分析了两级Buck电路组成的级联电源系统的启动瞬间稳定性，推导出启动稳定性的关键参数公式，得出电源参数设置方法及其对系统启动瞬间的稳定性影响，最后对电源系统进行行为级建模仿真，验证了启动稳定性关键参数公式，对系统工程参数设计具有指导意义。

1 级联电源系统启动稳定性分析

本文研究的分布式级联型电源系统采用两级BUCK变换，将500 V电压变换为+5 V负载用电电压。前级电源选用移相控制器UC3875构成移相全桥BUCK变换拓扑，实现电源隔离变换；负载电源选用内部集成功率管的LT8641 Buck控制器构成非隔离BUCK变换拓扑，实现对负载的快速响应。图1 展示了两级电源级联关系及相关无源器件的大信号模型。

图1 级联电源系统大信号模型

级联电源系统各电源模块的环路控制均具有软启动功能，不同的软启动控制方式对电源启动瞬间的环路特性有不同影响。

1.1 前级电源启动过程分析

级联电源系统中前级电源通常采用移相全桥Buck拓扑设计，利用恒定电流源为外置软启动电容充电实现软启动控制。以移相型控制芯片UC3875为例，其软启动原理如图2所示。

图2 UC3875软启动原理图

具体来说，软启动过程中因前级电源输出功率较大，为防止输出电压过冲，令软启动电容C上的电压V嵌位误差放大器输出E/AOUT端电压。同时，前级电源移相角大小由E/AOUT端电压决定，因此移相角随软启动电压值的增加逐渐放宽，对应的输出电压逐渐升高，直至达到目标电压值。

记图2控制芯片内部的软启动充电电流为I，与软启动电容上电压V的关系为：

设t为前级电源软启动时间，那么有：

因V直接嵌位误差放大器输出端E/AOUT电压，所以V电压与环路占空比成线性关系，该比例参数记为K。设D为软启动过程中环路占空比：

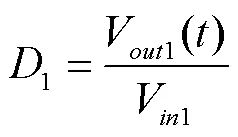
那么有：

此时可以得出图1中前级电源的输出电压：

前级电源空载软启动过程中的输出电流：

将(5)代入有：

然而，该软启动控制方法存在一定缺陷。在前级电源处于软启动过程中，输出电压V1升高到负载电源设置的启动点时，因容性负载C2较大，负载电压在建立瞬间向前级取电导致I2变大，而此时前级电源的移相角受软启动电压值嵌位，无法快速增加占空比对环路中的电感进行储能以响应负载的变化。因此负载电源输入电流I2主要由变换器负载电容C1提供，导致输出电压V1出现跌落。若跌落幅度超出负载电源启动关断滞环，负载电源将关断重启，从而造成供电链路震荡，同时可能会对负载的正常工作造成影响。

1.2 负载电源启动稳定性分析

负载电源LT8641 Buck控制器软启动的原理如图3所示。

图3 LT8641 Buck控制器软启动原理

LT8641内部的恒流源I2为外置软启动电容C2充电，当软启动电容电压V2()低于基准电压V2时，误差放大器同相端电压随V2()同步升高，经分压电阻1，2设置的输出电压V2()与V2()成线性关系，该比例参数记为K：

当V2()升高至基准电压V2，误差放大器同相端电压不再随V2升高，等于V2，经过控制环路调节，输出电压达到额定电压V2。

图2中软启动充电电流I2与外置软启动电容电压V()的关系为：

即：

图1中负载电容充电电流与负载电容电压的关系式：

将(8)、(9)代入(11)则有：

假设电压建立前负载芯片不工作，即软启动过程中阻性负载无穷大，负载电流公式为：

为简化计算，此处假设电源转换效率近似为100%，那么有：

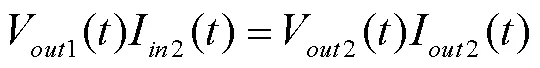
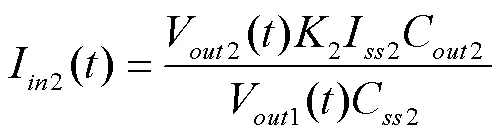
因负载电源软启动时间远小于前级电源软启动时间，因此负载电源的启动过程的V()可近似为负载电源启动电压阈值V，即：

1.3 级联电源启动稳定性分析

根据上文对前级和负载电源的分析，考虑最坏情况，当负载电源启动足够快，启动所需电流全部由前级电源输出电容提供，则图1中前级电源输出电容充电电流I1：

启动过程中前级电源输出电容上电压跌落值为：

代入公式(7)和(16)得：

即：

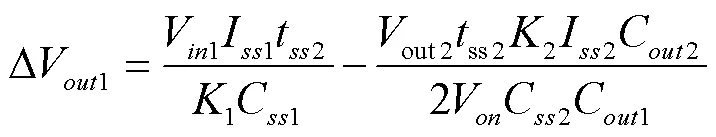
代入式(2)、(5)、(11)、(12)得：

当ΔVt≥0，即

负载电源启动时电压不会跌落。反之亦然。

当ΔV≤-V（负载电源启动滞环电压）即：

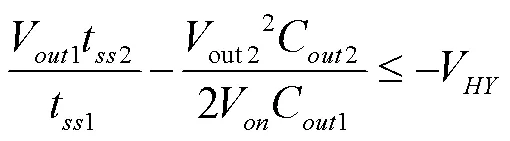
前级电源输出电压跌落至低于负载电源的关断电压时，负载电源将出现关闭重启现象。短时间内的多次重启可能导致负载芯片程序混乱，引发故障。而实际系统的传输线路中存在寄生参数，负载电源瞬间多次重启还会导致严重的线路震荡，存在芯片及电容过压烧毁的风险。

因此在级联电源系统的参数设置中需避免负载电源在开启瞬间出现关闭重启现象，即满足：

已知负载电源BUCK控制器LT8641使能端EN启动阈值V=1.0 V，滞环为45 mV，对输入电压进行电阻分压作为EN使能输入值，设置启动点，电源启动滞环为：V=0.045V，代入公式(24)得：

由上式可以得出，因系统输入输出电压确定，软启动电流由芯片内部已知电流源控制，因此，对于前级电源，增加其输出电容C1并减小其软启动时间t1有助于避免负载电源关断重启现象；对于负载电源，减小输出电容C2，增加其软启动时间t2，同时，增加其启动电压V同样有助于提升系统启动瞬间稳定性。由于成本及电源系统空间限制，前级电源输出电容并不能无限增大，而负载电源输出电容也需要根据负载特性及对电源纹波、脉冲峰峰值等需求选择足够的容量。因此，不能单纯通过调节供电链路电容来保证启动稳定性，还可以适当调节两级电源的软启动时间、设置合适的负载电源启动点及滞环区间，从而实现级联电源的启动稳定性。

2 级联系统建模仿真

对本文研究的两级级联电源系统进行行为级建模，模型如图4所示。负载电源一般为分布式的多个负载点电源并联，为方便仿真，此处将所有负载电源等效为一个电源，负载电容值C2为单路负载电容乘以倍数。系统参数设置如表1。

表1 系统仿真参数

图4 两级级联电源系统仿真模型

代入公式(25)，可计算出当V＞18.71 V时，级联电源系统启动过程不会出现重启现象。

图5所示为负载电源启动点V=15 V时的启动波形，其中V1为一次电源输出电压（母线电压），测量点为靠近负载电源的输入端口处，V2为负载电源输出电压。由于负载电源启动点设置过低，导致前级电源输出电压跌落值超出负载电源启动滞环，电压值低于负载电源关断电压，负载电源关断。此后前级电源输出电压继续升高，直至再次达到负载电源启动点，负载电源重新启动。如此往复，导致负载电源多次关断重启，同时仿真模型考虑了实际电源系统两级电源间的传输距离产生的寄生电感RL和RL，寄生电感的作用加剧了负载电源输入电压的振荡，电压最高振荡至38 V。负载电源输入电压的振荡不仅影响了负载供电的稳定性，还将给电源芯片带来过压损坏的风险。

图5 级联电源系统启动波形（Vout=32 V，Von=15 V）

图6为负载电源启动点设置为20 V时的启动波形，满足V＞18.71 V。负载电源启动瞬间，前级电源输出电压跌落值未超出负载电源启动滞环，负载电源不会出现关断重启现象，从而正常启动，保证了对负载的供电稳定性。

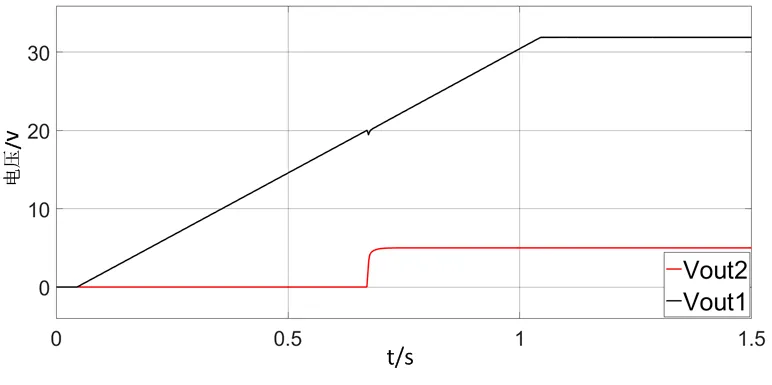
图6 级联电源系统启动波形（Vout=32 V，Von=20 V）

然而负载电源启动点并不是越高越好，实际工程应用中，一般将负载电源的启动点设置为前级电源额定输出电压的80%以下，以避免因线路损耗或干扰所产生的母线电压波动，导致负载电源无法启动或误关断。

3 结论

本文通过对分布式级联电源系统建立大信号模型，分析了其软启动过程中电压电容关系及出现关断重启的原因，推导出启动稳定性关键参数公式，并进行行为级建模仿真验证。结果表明，在满足电路性能需求的基础上，通过合理设置负载电源的启动点，同时综合考虑系统中储能电容的量值，以及电源软启动时间，从而满足推导得出的启动稳定性公式，可保证级联电源系统的启动稳定性。

[1] Shen X, Shu H C, Cao M, Nan Panand Junbing Qian. Influence of distributed power supply indistributed power distribution network[J]. Journal of Intelligent & Fuzzy Systems 2021,40: 7803-7810.

[2] Dale R. Patrick, Stephen W. Fardo, Brian W. Fardo. electrical power systems technology[M]. New York: River Publishers, 2021:217-249.

[3] Ma Z, AnTing, Shang Y W. State of the art and development trends of power distribution technologies[J]. Processing of the CSEE, 2016, 36(6): 1552-1567

[4] Alaboudy H K, Zeineldin H H. and Kirtley J L., microgrid stability characterization subsequent to fault-triggered islanding Incidents[J], IEEE Transactions on Power Delivery2012, 27(2): 658–669.

[5] SIMBURGER E J, RUMSEY D, HINKLEY D. Distributed power system for microsatellites[C]. IEEE Power Electronics Specialists Conference, 2005: 822-825.

[6] Meng H, Ji H Z, Sun J J, Wei L J, Zha X M. Bifurcation-based stability analysis of photovoltaic-battery hybrid power system [J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(3): 1055 - 1067.

[7] SEIYA A, MASAHIKO H, MASAHITO S. Optimal intermediate bus capacitance for system stability on distributed power architecture[C]. IEEE Power Electronics Specialists Conference, 2008: 611-616.

[8] Zhang X, Rua X B. Impedance-based local stability criterion for DC distributed power systems [J]. IEEE Transactions on Circuits and Systems I Regular Papers, 2015, 62(3): 916-925.

[9] 王伟, 宫池玉, 焦庆丽. 分布式电源级联系统稳定性分析与增强控制[J].电力电子技术, 2019, 53(11): 66-70.

[10] 张欣, 直流分布式电源系统稳定性研究[D]. 南京航空航天大学, 2014.

[11] He J, Wu X, Wu X, et al. Small-signal stability analysis and optimal parameters design of microgrid clusters[J]. IEEE Access, 2019, 7: 36896-36909.

[12] Yan Y J, Shi D, Bian D S. Small-signal stability analysis and performance evaluation of microgridsunder distributed control[J]. IEEE Transactions on SmartGrid, 2018, 10(5): 4848-4858.

[13] Abdelgabir H, Boynuegri A R, Elrayyah A. A complete small signal modelling and adaptive stability analysis of nonlinear _droop-controlled microgrids[C]. 2018 IEEE Applied Power Electronics Conference and Exposition(APEC), 2018:3333-3339.

[14] 夏绪伟, 罗全明. 变换器系统的小信号模型及稳定性判据[J]. 电力建设, 2015, 36(6): 96-102.

[15] 佟强, 张东来, 徐殿国. 分布式电源系统中变换器的输出阻抗与稳定性分析[J].中国电机工程学报, 2011, 31(12): 57-64.

[16] ERICKSON R W, CUK SLOBODAN R. Middlebrook D. Large Signal Modeling and Analysis of Switching Regulators [C]. IEEE PESC, 1982: 240-250.

[17] 杜韦静. 电流控制型DC-DC级联系统大信号稳定性关键问题研究[D]. 浙江大学, 2013.

[18] M. Kabalan, P Singh, Exploring the effect of grid impedance on the large signal stability of an inverter usingLyapunoy functions[C]. North American Symposium(NAPS), 2015:1-6.

[19] Han M, Wu C. Large signal stability analysis ofmulti-voltage level DC system[C]. IEEE Conference onIndustrial Electronics and Applications (ICIEA). 2021:1040-1045.

Research on the startup stability of the distributed power supply system

Ma Ning, Han Dong, Sun Yong

(Nanjing Research Institute of Electronics Technology, Nanjing 210013, Jiangsu, China)

TN86

A

1003-4862（2022）09-0056-05

2022-05-17

马宁（1989-），女，工程师，研究方向：开关电源技术、雷达电源系统等。E-mail：pfgmaning521@163.com