马尔可夫跳跃线性系统的符号稳定研究

王 恒，郭俊亮，唐孝国

（铜仁职业技术学院 信息工程学院，贵州 铜仁 554300）

马尔可夫跳跃线性系统是一类特殊的混杂系统，是由一族子系统和描述其之间联系的切换规则所组成，切换规则由马尔科夫过程控制，有关这类切换系统研究成果很多[1-8]，例如，指数几乎处处稳定，全局渐近稳定，均方稳定等[2-5]。其设计切换的方法也很多，如持续驻留时间，平均驻留时间等[6-8]。随着工程领域内的控制对象日益复杂，系统的模态不断增加，定量稳定难以求解，而一种定性稳定概念——符号稳定，为这个问题提供了一条新的思路，符号稳定由于其符号与矩阵元素的数值大小无关，作为一种天然的鲁棒稳定，不但简单直观，且一定程度上能够继承经典方法的设计经验，这也推动了鲁棒控制理论的发展。

给定一个实矩阵，仅保留其各元素的符号由此组成的矩阵称为这个实矩阵的符号型，符号型矩阵可视为一类特殊的矩阵，其元素均由符号{+，-，0}组成。而符号稳定[9]的概念最早出现在生态系统，在大规模的生物圈中，种群数量受多种因素影响且缺少精确的建模方法，但却呈现出很强的稳定性和抗干扰能力，这就促使研究人员利用符号稳定这种定性方法来分析不同物种间的动态变化过程，将这个变化过程与矩阵联系起来，通过分析雅克比矩阵的符号特征来研究动态系统的定性稳定性，（i，j）表示矩阵第i行第j列的元素，如果这个元素符号为正，表示物种j对物种i有积极影响，符号为负表示消极影响，零表示没有影响。这种联系可以用一个有向图来表示。例如，给定一个符号矩阵

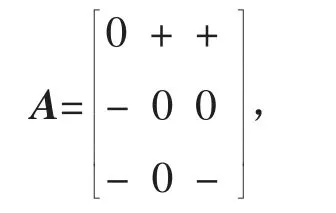
其有向图如图1所示。

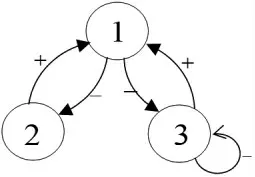
图1 A的有向图

相关研究者开始分析并运用符号稳定，得到了许多研究成果[9-11]。Jeffries[10]等用涂色测试法得到了符号稳定的充分条件，Rama[11]通过分析不同位置元素之间的联系提出了一种简单的符号稳定条件。基于这些研究，符号稳定在控制工程领域逐渐得到重视和应用[12-16]。相比于传统的Lyapunov稳定性理论，符号稳定应用更加广泛。

本文主要分析了符号稳定如何联系马尔可夫跳跃线性系统，目的是探索一种新的控制设计方法，基于马尔可夫跳跃线性系统的均方稳定，分析其子系统矩阵和转移概率矩阵的符号，得到了均方符号稳定，最后将得到的符号型代入数值进行验证。

1 问题描述

1.1 数学概念

Rn×n表示一个n维的实矩阵，In表示一个n维的单位矩阵。给定矩阵An×n=（aij）n×n，Aij表示矩阵的元素aij，diag An×n表示矩阵的对角线元素{a11，a22，…，ann}。给定矩阵Ai，i=1，2，…，n，blockdiag（A1，…，An）表示块对角矩阵。ei表示第i个元素是1，其余元素为零的列向量。sgn An×m表示矩阵An×m的符号型，GA表示sgn An×m的有向图。νec（A）在A上的作用是依A的列的顺序将A转化为一个列向量。⊗表示Kronecker积，⊕表示Kronecker和，其运算方式为

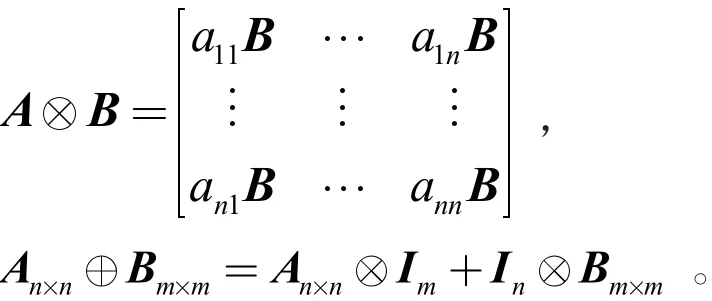
1.2 马尔可夫跳跃线性系统的均方稳定

考虑以下马尔可夫跳跃线性系统

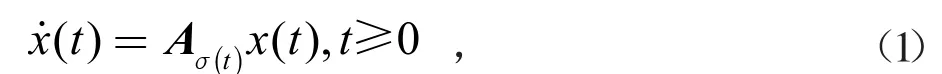
式中：x（t）是系统的状态向量；Ai为子系统矩阵；σ（t）是一个取值于{1，2，…，N}的齐次马尔可夫随机过程的有限状态。其过程σ（t）定义为

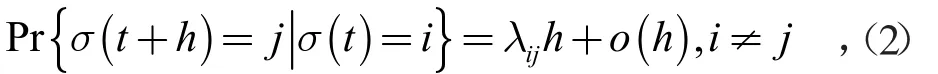
λij表示在时刻t从模态i经过h切到模态j的转移速率，且满足

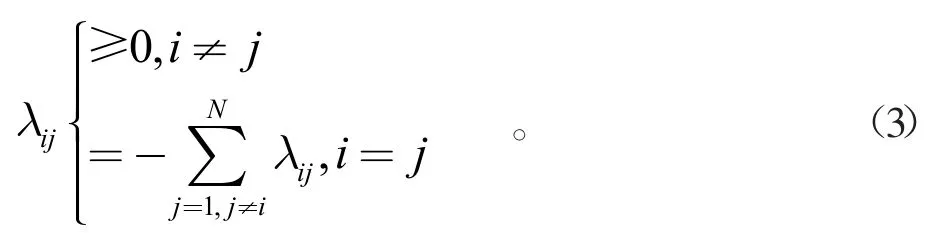
Λ=[λij]是σ（t）的转移速率矩阵。假设t=0时，k=0，在第k次跳跃之后的驻留时间是τk。令πi（t）=Pr{σ（t）=i}，并且其平稳分布Π=[π1，π2，...，πN]满足。式（1）和（2）被称为马尔可夫跳跃线性系统。

定义1[7]：对于任意初始条件x（0）和任意初始分布Π0，如果

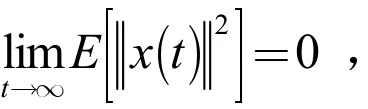
那么马尔可夫跳跃线性系统（1）和（2）被称为均方稳定的。

定理2[7]：系统（1）和（2）是均方稳定的，当且仅当存在对称正定矩阵，使得下面不等式成立，

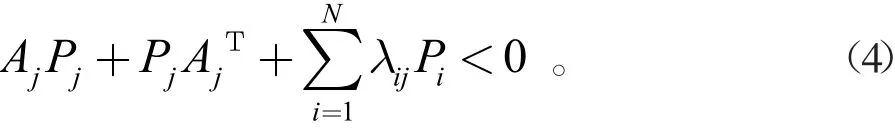
定理3：系统（1）和（2）是均方稳定的，当且仅当矩阵A'是赫尔维茨稳定的。

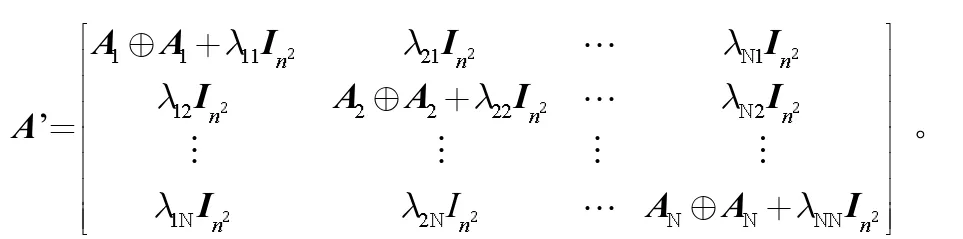
证明：由定理2可知存在对称正定矩阵Pi∈Rn×n使得式（4）成立，系统（1）和（2）是均方稳定的，那么利用由式（4）可得

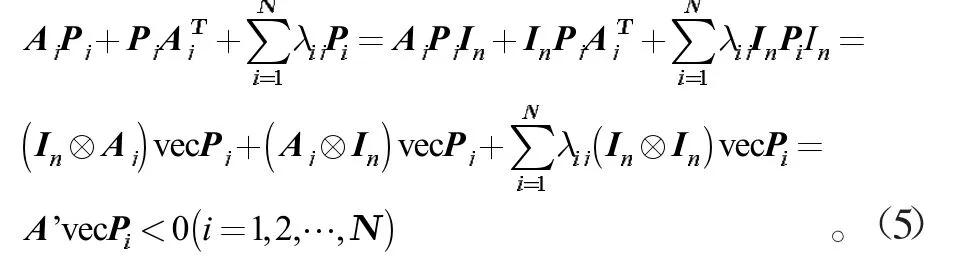
存在对称正定矩阵Pi∈Rn×n使得式（5）成立，当且仅当A'是赫尔维茨稳定的。

1.3 马尔可夫跳跃系统的定性特性

在接下来的分析中，只考虑A'的符号型，它们属于一个符号矩阵的集合，即一种定性的矩阵。

定义4[16]：符号矩阵是一个所有矩阵元素取值于集合S:={-，＋，0}中的矩阵。所有n行m列的符号矩阵可表示为Sn×m。

定义5[16]：一类定性的实矩阵An×m通过下面这个集合定义。

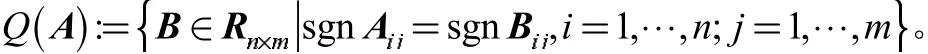
由定义5可知，Q（A）表示一类与A有相同符号的实矩阵，那么QS表示在Q（A）中，对于所有实矩阵A，有sgn Aij=Sij，令M满足式（3）的不可约矩阵，那么

为了分析马尔可夫跳跃线性系统的符号稳定，将式（1）描述为

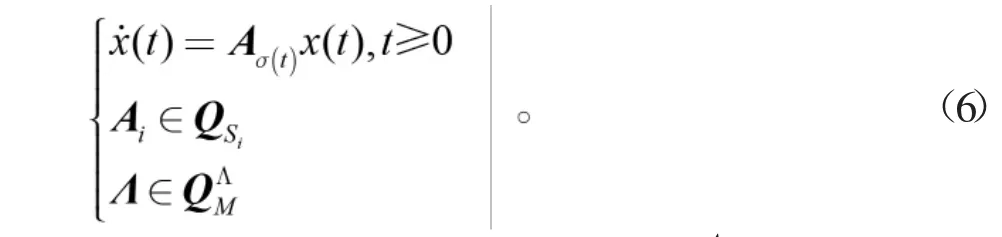
定义6[15]：如果所有使得系统（1）和（2）是均方稳定，那么称系统（6）是均方符号稳定。

1.4 符号稳定的概念及性质

这篇文章将符号稳定的概念引入马尔可夫跳跃线性系统，目的是探索一种新的控制设计方法。接下来将定义符号稳定，并分析它的相关性质。

定义7[12]：如果与实矩阵An×n有相同符号型的任意实矩阵An×n都是赫尔维茨稳定的，则称sgn An×n是符号稳定的。

说明8：矩阵An×n=（aij）n×n满足aijaji=0（i≠j）和aijajk…aqrari=0，则称GA是非循环的。

定理9[15]：如果GA是非循环的，则存在一个置换矩阵Q，使得QTAQ是一个上三角矩阵。

定义10[13]：定义各个符号型并运算如下。

（1）如果各符号型同一位置处的各元素为某一相同符号或0，则并运算结果对应位置处的元素为该符号（非0）。

（2）如果各符号型同一位置处的各元素均为0，则并运算结果对应位置处的元素为0。

（3）如果各符号型同一位置处的各元素异号，则并运算结果对应位置处的元素记为*，表示可取任意符号。

上述并运算结果所得矩阵为各个符号型的源符号型矩阵。

定理11：盖尔斯果林圆盘定理。

一个n阶矩阵An×n=（aij）n×n的全部特征值包含在以下的n个圆盘中：

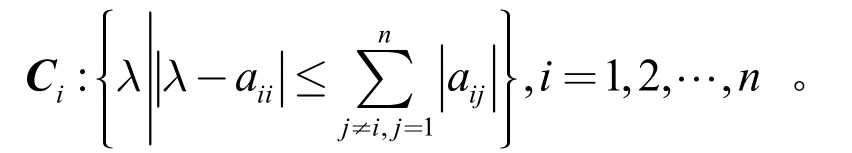
定理12[11]：如果一个符号矩阵A可以分为A1，A2，…，Aq，且det A=det A1×det A2×…×det Aq，那么A是符号稳定的，当且仅当A1，A2，…，Aq全部是符号稳定的。

2 马尔可夫跳跃线性系统均方符号稳定分析

给定马尔可夫跳跃线性系统（6）的子系统矩阵Ai和转移概率矩阵Λ，令

注意，S'和Si分别是A'，Ai的符号矩阵。通过分析Si和Λ之间的联系可以分析S'的符号稳定。

定理13：R是Si的符号矩阵集合的源符号型矩阵，下面两个命题等价：

①马尔可夫跳跃线性系统（6）是均方符号稳定的；

②GR是非循环的，diag R＜0且diag Si＜0。

证明：马尔可夫跳跃线性系统（6）是均方符号稳定的，根据定义6，所有，使得系统（1）和（2）是均方稳定的，又由定理3可知，系统（1）和（2）是均方稳定的，当且仅当矩阵A'是赫尔维茨稳定的，所以马尔可夫跳跃线性系统（6）是均方符号稳定的，等价于S'是符号稳定的。R是Si的符号矩阵集合的源符号型矩阵，GR是非循环的，由定义10可知，所有GSi是非循环的，令

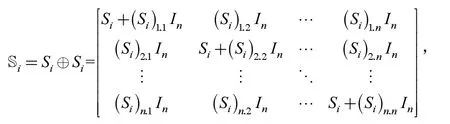
那么

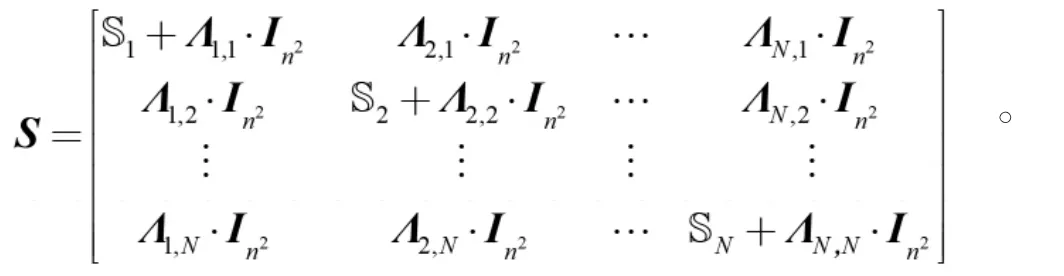
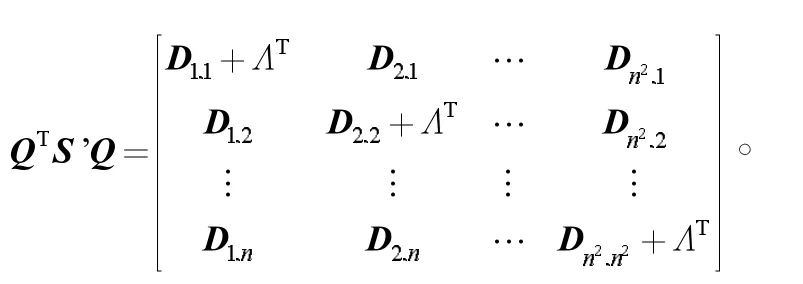
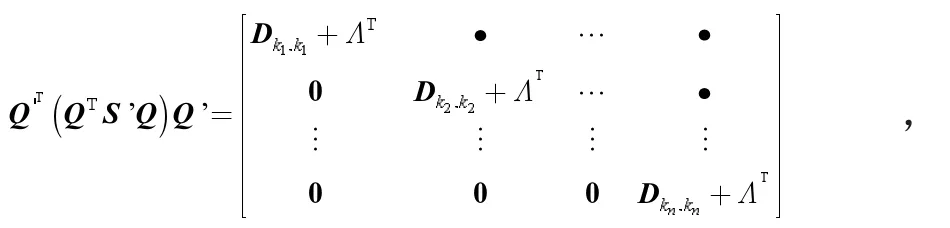
式中：0表示零矩阵；·表示矩阵元素不全为零的Di,ν或Dν,i，如果S'是符号稳定的，等价于QTS'Q是符号稳定的，等价于Q'T（QTS'Q）Q'是符号稳定的，由定理12可知，如果Q'T（QTS'Q）Q'是符号稳定的，当且仅当Dki，ki+ΛT（i=1，2，…，N）是符号稳定的，即Dki，ki+Λ（i=1，2，…，N）是符号稳定的。下面证明Dki，ki+Λ（i=1，2，…，N）是符号稳定的。

因为Si的对角线元素小于零，所以Dki，ki的对角线元素全部小于零，Λ满足式（3），即，那么，由定理11可知，的特征值分布在如图2所示的圆盘内，所以Dki，ki+Λ（i=1，2，...，N）是符号稳定的。

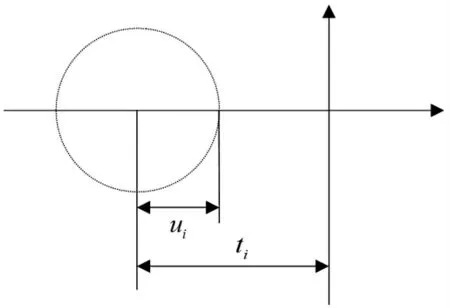
图2 特征值分布

3 符号例子和数值例子

对于马尔可夫跳跃线性系统（6）的均方符号稳定，令N=3，对于定理13的命题②，选择源符号型矩阵为

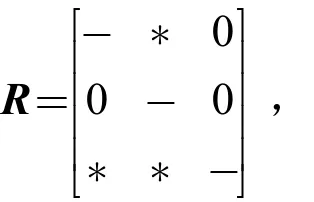
那么

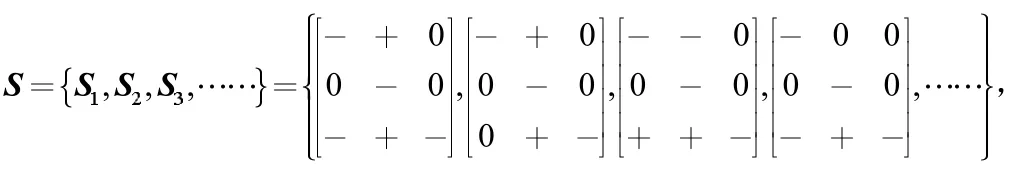
在集合S中任意选择符号矩阵作为子系统矩阵的符号矩阵，例如，

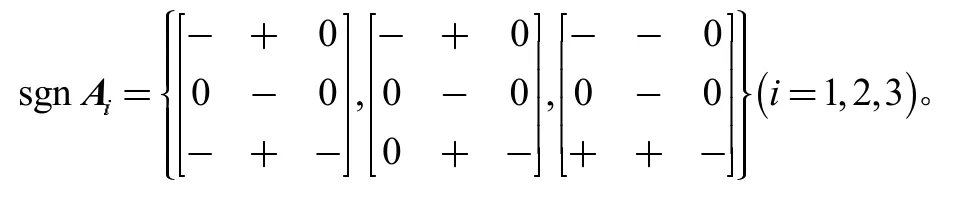
令马尔可夫切换信号σ（t）的转移速率矩阵为

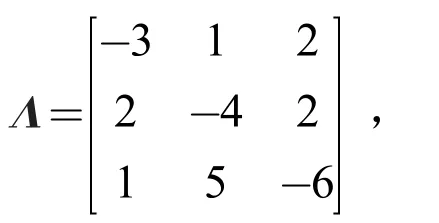
在符号矩阵中代入任意数值检验系统（1）的均方稳定，例如，

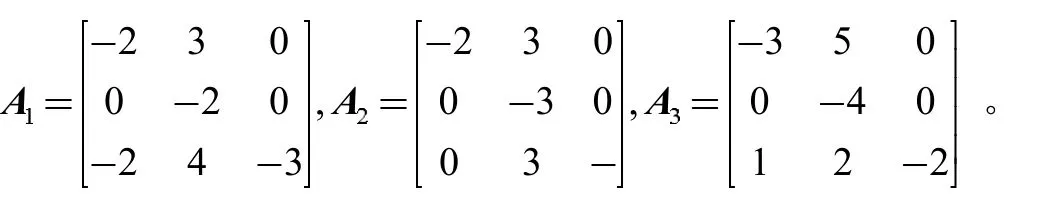
解线性矩阵不等式（4）得

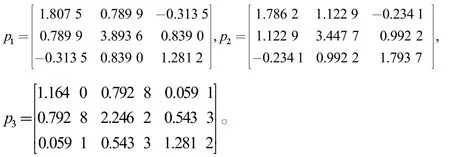
图3为马尔可夫跳跃线性系统（1）的均方稳定的7次状态轨迹，均为稳定状态。

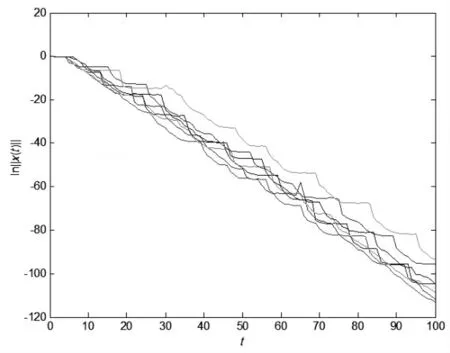
图3 的7次实现

4 结论

本文基于马尔可夫跳跃线性系统均方稳定的基础上，考虑到随着系统的复杂度增加，其线性矩阵不等式的可解性无法保证，所以将符号稳定引入马尔可夫跳跃线性系统，分析其定性稳定性，得到了马尔可夫跳跃线性系统均方符号稳定，有效地解决了可解性无法保证这个问题，最后通过一个符号例子和数值例子对其进行验证，证实了其有效性。