基于RBF的VSG转动惯量和阻尼系数自适应控制策略

高子轩, 赵晋斌，杨旭红，姚凤军，方剑峰

(1.上海电力大学自动化工程学院，上海市 200090；2.上海电力大学电气工程学院，上海市 200090；3.国网浙江省电力有限公司绍兴供电公司，浙江省绍兴市 312099)

0 引 言

随着“碳达峰”与“碳中和”政策的提出与推进，以可再生能源为主要能量来源的微电网备受瞩目。其中太阳能、风能等新能源需通过电力电子变换器接入电网，这些变换器具有控制灵活、响应迅速等特点，但却缺乏惯性和阻尼，所以其抑制波动和干扰的能力较弱且不能为电网提供惯量。为此，国内外学者提出了虚拟同步发电机(virtual synchronous generator, VSG)的并网逆变器控制策略[1]。与传统并网逆变器不同，VSG通过模拟同步发电机的惯性和阻尼特性，在功率平衡被破坏时，可通过虚拟惯量和阻尼动态补偿功率差额，减小频率波动，对系统的振荡起到一定的抑制作用[1-3]。

但是，由于虚拟同步发电机是通过电力电子变换器模拟同步机实现功率补偿，其本质仍是电力电子变换器实现的，当电网频率或输入输出功率发生了较大波动时，暂态过程中的冲击和振荡可能超过器件承受阈值，导致器件损坏，甚至影响系统稳定[4-5]。于是有研究人员提出，通过自适应调节转动惯量和阻尼系数提高系统的稳定性[6]。文献[7]提出通过乒乓算法对转动惯量进行调节，但由于乒乓算法只能对转动惯量进行离散的改变，会使得系统在调节时波动较为明显。紧接着文献[8]将模糊算法引入至控制策略中，使得转动惯量在调节时更为平滑，但模糊算法中的模糊规则和隶属度函数是完全通过研究人员的经验决定。而在文献[9-12]中，通过分析同步发电机的角频率与惯量之间的函数关系，建立近似的线性关系来调整惯量，解决了乒乓算法存在的离散控制问题。在文献[10-12]中更是引入了自适应阻尼系数完成对系统的控制，提升了控制效果。根据文献[13]，惯性J和阻尼系数D与角频率ω之间的关系是非线性的。因此，需要使用一种用于解决非线性问题的算法，此种算法既不会因为复杂的计算过程影响电力电子设备的反应速度，又能解决惯性J和阻尼系数D与角频率ω之间的非线性问题。在文献[14]中，通过径向基函数(radial basis function, RBF)神经网络算法对转动惯量进行了调整，初次将人工智能算法引入电力电子控制策略中，但该文并未对阻尼系数的控制给出具体方案，也并未发掘RBF神经网络针对多输入多输出系统所具有的优势。

综上，本文提出一种基于RBF神经网络的虚拟同步机控制策略。先通过传统虚拟同步发电机的数学模型、输出特性和小信号模型三个角度对转动惯量和阻尼系数进行分析，并计算其取值范围。接着结合RBF神经网络与虚拟同步发电机的特点，设计双输入双输出的RBF神经网络，同时对VSG的转动惯量和阻尼系数进行调整。最后通过仿真与传统控制策略进行比较，验证本控制策略的有效性。

1 VSG参数范围确定

1.1 改进型VSG控制原理

基于RBF神经网络的VSG控制原理如图1所示，虚拟同步发电机整体由分布式储能单元、三相逆变器、LCL滤波器组成。而改进VSG算法通过作用于三相逆变器完成对系统的控制，改进VSG算法包括：虚拟调速器(模拟同步发电机调速器)、虚拟励磁器(模拟同步发电机励磁器)、摆动方程(模拟同步发电机外部特性)和RBF算法(对转动惯量和阻尼系数进行调节)。其中Lf为逆变器侧电感，Lg为电网侧电感，Cf为逆变器侧电容。

图1 基于RBF神经网络的VSG控制原理图

(1)

P0=T0ω≈T0ω0

(2)

Pe=Teω≈Teω0

(3)

式中：J表示转动惯量；Dp表示虚拟阻尼系数；ω表示电网角频率当前值；ω0表示电网角频率参考值；T0表示机械转矩；Te表示励磁扭矩；P0表示机械功率；Pe表示电磁功率。

图2(a)为VSG中的有功功率控制回路，可以用公式(1)表示，其主要作用为模拟同步发电机的转动惯量和阻尼系数。图2(b)为VSG无功功率控制回路，其主要作用是模拟同步发电机的励磁器，公式如下：

(4)

式中：K为无功调压系数；E为逆变器输出侧单相电压有效值；Ug为电网电压有效值；U0为相电压参考值；Qe是输出无功功率测量值；Q0是无功功率参考值。图2(b)中，U是VSG输出端电压，即公共连接点(point of common coupling，PCC)耦合点电压。

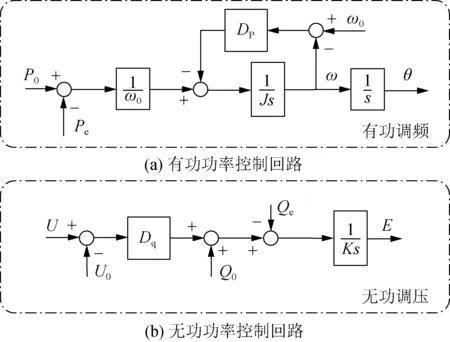
图2 VSG有功功率和无功功率控制回路

图3为接入VSG后的并网等效电路。图3中，Zg为电网阻抗，Zf为逆变器的输出阻抗，r为等效电阻，X为等效感性分量。令Z∠θ为VSG的等效输出阻抗，一般情况下X>>r，为了便于分析，本文令Z∠θ≈X∠90°。

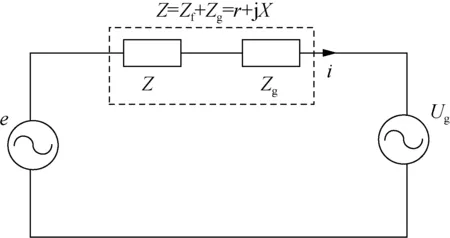
图3 VSG并网等效电路

通过联立同步发电机的有功功率和无功功率公式，可得如下VSG稳态方程：

(5)

式中：δ为功角；E0为逆变器输出侧单相电压有效初始值；Q为输出无功功率。

1.2 转动惯量和阻尼系数对虚拟同步发电机特性的影响

1.2.1 对有功功率输出特性的影响

对时域方程式(5)进行扰动分离和线性化。δn为工作时功角变化量，考虑到同步电机的功角特性，在正常工作状态下δn很小，因此可以近似：sinδn≈δn，cosδn≈1，U0≈E。同时根据转子运动方程和小信号假设可得，有功输出与角频率的小信号[14]为：

(6)

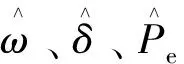
(7)

求得二阶系统特征根s1,2为：

(8)

其中：

(9)

式中：ξ为阻尼比；ωn为自然振荡频率。

若取ξ∈(0,1)，误差带为±5%，则本系统对应的超调量σ和调节时间ts为：

(10)

(11)

式中：Kω为调差参数。

在给定有功功率为10 kW和无功功率为5 kV·A的情况下，系统的有功功率动态性能完全由转动惯量J和阻尼系数Dp决定。在不同转动惯量和阻尼系数下，可绘制VSG的有功功率动态响应轨迹，如图4所示。图4(a)的分析显示，假定阻尼系数Dp保持不变时，转动惯量J与阻尼比ξ呈反比例关系，而与超调量σ呈正比，J越小，则ξ越大，σ越小，同时调节时间ts也越短；从图4(b)可以分析出，假定J保持不变，Dp与ξ也存在正比例关系，而与σ呈反比例关系，Dp越小，则ξ越小，超调量σ会越大且调节时间ts也会变长。由此可以得出结论：转动惯量决定了VSG有功功率动态响应期间的振荡频率，而阻尼系数决定了VSG有功功率动态响应过程的衰减率[4]。

图4 不同转动惯量和阻尼系数下的输出有功动态响应

1.2.2 对角频率输出特性的影响

图5为在给定有功功率为10 kW和无功功率为5 kV·A的情况下，角频率波动变化评价指标过冲量Δωmax与调节时间ts。

从图5(a)可得，仅从角频率的过冲量 Δωmax来看，增大阻尼系数Dp和转动惯量J都可以减少系统波动时角频率的超调量。而从图5(b)可以看出，当转动惯量J越小时，调节时间就越小；但阻尼系数Dp对调节时间的影响却呈现先减后增的变化，这是由于阻尼系数Dp过小系统波动会产生较大超调，而小阻尼无法快速调节过大波动，所以适当增大阻尼会减少调节时间ts，但接着增加阻尼系数Dp会使得系统响应速度变慢而增加调节时间ts。由此可以得出结论：转动惯量J设置的越大，系统角频率波动越小，系统越稳定，但J也不能设置得太大，否则系统的稳定性会变差。考虑阻尼系数时，从公式(1)可得，当T0-Te-Jdω/dt保持不变时，阻尼系数Dp越大，角频率的偏移量Δω越小，但过大的阻尼可能会导致系统响应速度变慢。

图5 不同转动惯量和阻尼系数下系统角频率的评价指标变化

1.3 转动惯量和阻尼系数取值范围的确定

本文中阻尼系数Dp取值范围，可通过逆变器接入电网连续运行的电网标准EN50438[15]获得，电网频率的变化偏差在±1 Hz，本文设计逆变器的额定容量为50 kV·A，而逆变器的有功功率输出范围为其额定容量的40%～100%[16]。由此可以得出阻尼系数Dp的取值范围：

(12)

式中：ΔT为角频率变化对机械转矩的影响值；ΔP为有功功率的可变化量，也是逆变器的额定容量。所以Dp的取值范围为[10，25]。为保证系统稳定，将系统阻尼比ξ设置在(0.7 , 1.0)，根据公式(9)得：

(13)

求得转动惯量J取值范围为[0.035,0.450]。

2 基于RBF的VSG控制策略设计

与多层前馈网络系统相比，RBF系统的网络结构更加简单且泛化能力突出，系统运行中不需要依托大量的数据计算。而RBF神经网络在任意精度取值情况下都具备非线性函数的特征[17-18]，这些特点刚好适配VSG的调参特性，既不会影响电力电子设备的反应速率，同时又解决了参数间存在的非线性问题。

图6为结合VSG控制策略的特点所设计的RBF神经网络结构图，其中j、i、l分别代表输入层、隐藏层和输出层。

图6 针对VSG控制的RBF神经网络结构图

为了便于区分，公式中变量分别用上标(1)、(2)、(3)表示输入层、隐藏层和输出层。

从图6可以看出，输入层的输出为：

(14)

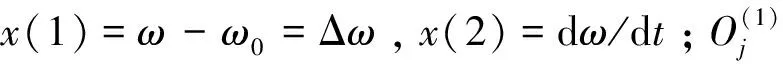
隐藏层的输入是：

(15)

隐藏层的输出是：

(16)

隐藏层的函数g(x)为高斯函数：

(17)

神经网络输出层的输入是：

(18)

神经网络输出层的输出是：

(19)

(20)

(21)

式中：u1是转动惯量的上限；u2是阻尼系数的上限。

该神经网络的评价函数如下：

(22)

本文通过梯度下降法对隐藏层中的权值进行更新，同时为了提高算法的寻优速度，引入了惯性环节。

(23)

式中：η是学习率；α是惯性系数。

(24)

(25)

在更新权重的过程中，需要系统的Jacobian矩阵。由于Jacobian矩阵计算过于复杂，本文采用了摄动法和符号函数法结合的方法来处理此问题。

首先通过摄动法，用Δω/ΔJ来代替∂ω/∂J：

(26)

接着通过符号函数法，用sgn(Δω/ΔJ)来代替Δω/ΔJ。因此，∂ω/∂J可以用符号函数代替，如式(27)所示。替换过后可能会导致出现误差，但在神经网络中可以通过学习率η进行调整。

(27)

同理，∂ω(k)/∂Dp(k)可以用符号函数代替，如式(28)所示：

(28)

综上所述，RBF神经网络的权值更新公式为：

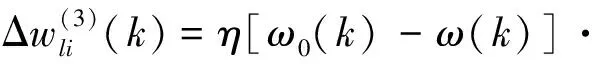
(29)

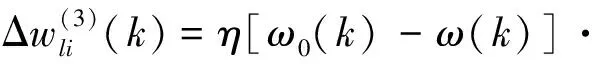
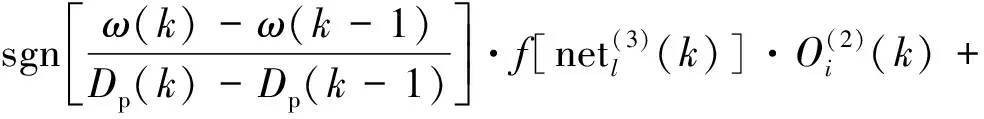
(30)

图7为基于RBF神经网络的VSG控制算法流程图。从图7可以看出，整个过程由摆动方程确定此刻角频率，经过RBF神经网络得到需要调节的转动惯量和阻尼系数，再根据取值范围确定转动惯量和阻尼系数，返回至摆动方程得到下一刻角频率，完成整个闭环控制。

图7 RBF-JD控制流程图

3 仿真验证

为了验证所提出的控制策略的正确性和优越性，利用MATLAB/Simulink软件搭建了VSG系统，仿真模型参数如表1所示。在初始阶段，系统连接10 kW的有功负荷和5 kV·A的无功负荷，在0.6 s时有功负荷突然增加至20 kW，在1.1 s时负载立即恢复到初始状态，无功负荷恒定在5 kV·A。

表1 仿真模型主要参数

在相同的仿真条件下，除了非自适应控制和基于RBF-JD控制，本文还将使用文献[11]与文献[14]中的控制策略进行对比与验证。其中非自适应控制选择的转动惯量为0.25 kg·m2，阻尼系数是20 N·s·m-1。自适应线性控制策略中主要参数如表2所示。

表2 自适应线性控制策略主要参数

固定阻尼系数用RBF调整转动惯量J的控制策略中主要参数如表3所示。

表3 RBF-J算法主要参数

不同策略的功率控制效果如图8示。其各算法的各项分析指标如表4所示。当有功功率在0.6 s突然增加的情况下，线性控制算法、RBF-J和RBF-JD算法控制效果基本类似，有功功率的过冲量ΔPmax分别为1.95 kW、1.95 kW、1.20 kW，其对应的超调量σ都远小于固定参数，分别为9.75%、9.75%、6.00%；而在恢复到稳态的调节时间上，线性控制算法调节时间为0.17 s，RBF-J和RBF-JD算法则是在调节时间上完全相同，为0.09 s后就达到了稳定状态。而当有功功率在1.1 s回到初始状态时，RBF-J和RBF-JD的超调量都有所下降，RBF-JD的超调量仍然是最小的，而线性算法控制效果与功率突增时类似；在恢复过程中，各个算法的调节时间与功率突增时几乎相同。

图8 不同控制策略下的有功功率对比

表4 两个场景下不同控制策略的分析指标

不同策略的角频率控制效果如图9所示。当有功功率在0.6 s突然增加时，角频率升高。与固定参数相比，线性控制、RBF-J、RBF-JD控制的角频率偏差都较小。它们在频率恢复过程中的控制效果差异很大。其中，利用RBF神经网络控制的两种算法其角频率可快速恢复至314.15 rad/s，线性控制算法则需要经过些许振荡才能恢复平稳。当有功功率在1.1 s回到初始状态时，有功功率突然下降使得角频率骤减，线性控制的角频率偏差明显要小于两种RBF神经网络控制，但在恢复过程中的表现则不如RBF神经网络。而对比RBF-J和RBF-JD两种控制算法可以发现，在有功功率发生跌落时，RBF-JD对系统的稳定性控制效果要稍优于RBF-J。

图9 不同控制策略下的角频率对比

线性控制与RBF自适应控制转动惯量和阻尼系数变化对比如图10所示。如果只分析角频率和有功功率变化，线性控制和两种RBF神经网络控制效果差异较小。但是从图10可以看出，三种算法对虚拟惯量和阻尼系数的控制是完全不同的。当频率处于稳态区间时，线性控制的虚拟惯量和阻尼系数还是会进行多次调节，但是对于RBF神经网络控制，减少了很多冗杂的控制动作。这是因为RBF神经网络在控制过程中，对转动惯量阻尼系数的学习权重进行了优化，在经过一定次数的学习后，在当前系统中，RBF神经网络已经能通过当前信息迅速地得到较为合适的控制参数。

图10 不同控制策略下的转动惯量和阻尼系数变化对比

4 结 论

本文通过对VSG有源环路进行小信号建模，针对相关参数与VSG角频率和角频率变化率之间的非线性关系，提出一种在复杂并网过程中基于RBF的非线性控制策略，并得出以下结论：

1)通过分析不同转动惯量和阻尼系数下系统有功功率和角频率评价指标的变化关系，可知转动惯量和阻尼系数对评价指标影响复杂，因而无法通过单一变量的调节实现有效控制。

2)结合RBF控制策略，控制过程无需对转动惯量和阻尼系数耦合关系进行分析，因而可有效提升控制效果。同时，由于RBF神经网络的学习特性，后续控制过程可持续优化，继而参数的调节频率可进一步减小。

3)相较于通过RBF只调节转动惯量的方法，本文引入了阻尼系数对系统的影响，在加入通过RBF调节的阻尼系数后，系统在面对有功功率波动时也会更加稳定；RBF对两个参数同时调整也会使得RBF在学习过程中更快优化。