计及日前-实时交易和共享储能的VPP运行优化及双层效益分配

郑浩伟，闫庆友，尹哲，党嘉璐，林宏宇，谭忠富

(华北电力大学经济与管理学院，北京市 102206)

0 引 言

随着碳中和、碳达峰目标的提出，构建新型电力系统已成为未来电力能源的发展方向[1-2]。但由于风光存在不确定性，高比例接入将对电力系统的安全稳定和灵活运行带来挑战，因此弃风弃光现象产生[3]。虚拟电厂(virtual power plant，VPP)技术通过整合分布式发电单元、储能装置以及柔性负荷等灵活性资源，能够有效减少弃风弃光[4]，提高电力系统灵活性[5]。由此，VPP优化调度成为热点问题，大量学者展开了研究[6-8]。文献[6]基于VPP中不确定性因素在不同时间阶段的协调互动，构建了考虑主动配电网效益和VPP效益的双层优化模型，有效提升了VPP的市场竞争力和灵活性。文献[7]利用5G基站储能技术平移风光出力波动，构建了VPP调度优化策略，结果表明基站储能能够减少基站用电成本，降低VPP运行与投资成本，同时提高可再生能源消纳水平。文献[8]考虑接入储能、可中断负荷、燃气轮机等多种分布式能源，提出了虚拟电厂辅助参与配电网灵活性优化策略。上述文献验证了虚拟电厂在资源整合、灵活调度问题上具有一定的优越性，其中储能系统的加入发挥了极大作用。但从目前实际情况来看，储能技术在应用过程中成本较高，依靠单一主体运营，经济性和利用效率受限[9-10]。

随着共享经济的兴起，共享储能使储能系统在能源互联网中的应用进一步得到发展[11]。文献[12]将共享储能引入新能源场站提供调频服务，以储能利益最大化为目标，考虑储能寿命和电量维持等因素，构建了日前优化模型，结果表明通过参与二次调频和峰谷套利，共享储能能够被有效利用，从而达到利益最大化。文献[13]提出了一种点对点交易下的储能聚合商交易模型，通过储能共享和电能自营模式，完成智能合约交易匹配，该模型的便利性和经济性得到了验证。文献[14]构建了含共享储能的社区综合能源系统用户协同优化模型，充分考虑用户的购电成本、社区运营商购能成本、储能租赁费用，建立了用户整体经济最优的优化目标函数，该模型能够帮助用户合理安排用能计划，降低用能费用。现有文献已验证了共享储能的经济效益和资源利用效率方面的可行性和优越性，但未充分考虑收益的分配问题。共享模式下，合理公平的效益分配是调动参与主体合作积极性的重要保障，同时也能够更加明确参与主体对联盟体的贡献程度，从而量化共享储能的合作价值。

文献[15]对比了多类型用户聚合时分散式储能配置和一体化配置2种方式的经济效益，采用Shapley值法针对2种模式下用户效益进行分配，最终得出分散式共享储能的模式能够获得更大的效益。文献[16]提出多微电网并网系统租赁共享储能组成微电网联盟参与配电网调峰调度的优化调度策略：第一阶段中优化储能应用，按需租赁储能；第二阶段对微网联盟进行优化，通过成员间新能源功率互济达到效益最大化，最终通过Shapley值法分配合作剩余。文献[17]采用两阶段法对多微网共享储能进行优化配置和成本分摊。在第一阶段，获得共享储能优化配置下的成本；在第二阶段基于线路功率损耗提出改进Shapley值法，分摊共享储能成本。上述文献不仅验证了公平合理的效益分配对含共享储能能源系统调度的积极作用，同时也验证了Shapley值法在效益分配中的适用性。但是，所分配的效益存在差异，文献[15-16]针对整体效益进行分配，而文献[17]针对共享储能效益进行分配，尚未有文献针对含共享储能的双层结构效益分配进行研究。

综上所述，本文以风光出力偏差为变动因素，引入日前-实时两级市场交易，构建含共享储能的VPP调度优化模型；基于合作博弈理论，引入Owen值法(即双层Shapley值法)，提出含共享储能的VPP优化效益的均衡分配策略。

1 电力市场环境下含共享储能的VPP系统结构设计

1.1 VPP物理结构

单一的源侧或者荷侧资源容量较小，达不到电力市场的准入门槛，无法充分发挥其在电力系统中的灵活性[18]。因此，需要通过VPP聚合分布式电源、柔性负荷和分布式储能等灵活性资源参与电力市场交易。本文所研究的VPP主要是由风电机组(wind power plant，WPP)、光伏机组(photovoltaic，PV)、柔性负荷和储能系统组成，其物理结构如图1所示。

VPP内部参与者关系为：可再生能源优先通过内电网向VPP内部负荷供电；储能系统通过内电网在电价谷时段充电，峰时段放电；当出现电量缺口时，VPP优先向灵活性资源发出调度指令，即共享储能放电和柔性负荷需求响应来消除偏差，再从电力市场上购电以满足电力需求；当出现电量剩余时，经由外电网在电力市场上出售。

1.2 共享储能机制

储能系统的配置可以进一步减少高渗透率下可再生能源发电带来的出力波动，提高VPP运行的可靠性[1,19]。储能系统可以在用电低谷时段储存可再生能源的多余电力来促进可再生能源的消纳；同时，在用电高峰时段释放存储的电力来减少VPP从外电网购买的电量，降低VPP的购电成本[20]。然而就目前而言，储能系统的高投资成本是限制其商业化发展的主要障碍[21]。VPP运营商可借鉴共享经济概念，基于实时通信技术聚合，建立共享储能平台，协调运行多个孤立的储能单元，在满足VPP削峰填谷需求的同时，进而降低储能系统的投资和运维成本，提高VPP的经济性[22]。

本文所提VPP内共享储能系统结构如图2所示。共享储能系统的各个储能单元都配备一个单独直流隔离器，在充、放电过程中起到保护作用。各个储能单元通过DC/DC模块与公共直流母线相连，可实现共享储能系统内部能量交换。再通过一个总的AC/DC模块连接公共直流母线和VPP的内电网。受益于AC/DC模块和DC/DC模块的潮流可控性，通过在模块中增加计量单元和实时通信控制单元，可以将VPP交流电网产生的电量剩余/不足信息由AC/DC模块传递到公共直流母线另一侧的DC/DC模块，再由DC/DC模块将信息转换为储能单元充、放电操作，这样可以实现共享储能系统与VPP其余部分的能量交换和储能单元充、放电的电量计量。

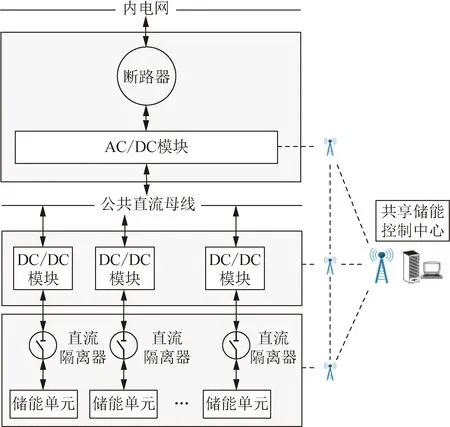
图2 共享储能系统结构

1.3 两级电力市场交易机制

两级电力市场交易机制如图3所示。本文考虑了一个具有日前市场、实时市场的两级交易机制的电力市场。在两级市场中，VPP作为价格接受者，完成日前的风光出力预测，并基于此向电力市场申报次日24 h的投标电量。由于风光出力预测偏差的存在，当VPP内的储能系统充、放电和柔性负荷需求响应无法消除风光出力偏差时，VPP需要在实时市场交易中消除出力偏差。如果VPP实时发电量超过其在日前市场投标电量，则其多余的发电量将以正失衡电价平抑，正失衡电价低于或等于日前市场出清价格。如果VPP实时发电量低于日前市场投标电量，则其发电赤字要以大于或等于日前市场出清电价的负失衡电价平抑。日前、实时电价模型为：

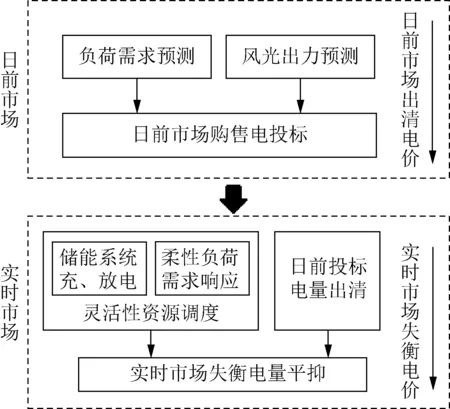
图3 两级电力市场交易机制

λrmb(t)=(1+σp)λbm(t)

(1)

λrms(t)=(1-σp)λbm(t)

(2)

式中：λrmb(t)、λrms(t)分别为t时刻的实时市场负失衡电价和正失衡电价；λbm(t)为t时刻的日前市场出清电价；σp为实时市场失衡电价惩罚系数。

2 含共享储能的VPP运行优化模型

2.1 机组模型构建

2.1.1 风光机组模型及不确定性处理

1)风光机组出力模型。

风电机组出力[23]由风速的随机性决定，一般使用分段函数来近似表示风电输出功率Pwpp(v)。

(3)

式中：Pwppr为风机的额定功率；vi、vr、vo分别为切入风速、额定风速、切出风速；v为风速，其中v服从双参数Weibull分布概率密度函数，表达式f(v)为

(4)

式中：k为形状参数，k>0；c为尺度参数，c>1，可由该时段的风速均值和方差求得。

本文首先采用场景生成-削减方法生成各时段风速数据，然后由式(3)所示的风电机组与风速之间的关系式来计算风电机组出力功率预测值。

光伏机组的实际输出功率[24-25]受太阳辐射强度、环境温度和额定功率等因素影响，因此光伏机组的输出功率可由其标准测试条件下的输出功率、光照强度、环境温度等与实际工作条件下的实际数值对比估算得到。

(5)

式中：Ppv(G,T)为光伏机组实际输出功率；G和T分别为实际光照强度和实际工作温度；Pstc、Gstc、Tstc分别为标准测试条件下的输出功率、光照强度和环境温度；g为功率温度系数。

据统计，一段时间内的太阳辐射强度是一个服从Beta分布的随机变量，其概率密度函数f(G/Gmax)[25]可以表示为：

(6)

式中：Gmax为该段时间内的最大光照强度；Γ为Gamma函数；α、β为Beta分布的形状参数，可由这一段时间内光照强度的平均值μG和标准差σG得到α。

(7)

(8)

本文首先根据当地各时段的气象预测数据获得太阳辐射强度和气温的数据，由功率估算公式和光照强度的概率密度函数求出光伏输出功率的概率密度分布为：

(9)

2)风光出力不确定性处理。

风光出力不确定性可通过多场景生成和削减技术进行处理。场景生成采用拉丁超立方抽样方法(Latin hypercube sampling，LHS)，该方法可使发生概率高的场景在样本空间中聚集[26]。LHS能够对累积概率曲线分层抽样后再取得样本数据，因此能够保证样本整体空间全覆盖。LHS算法流程[27]如图4所示。

图4 LHS算法流程

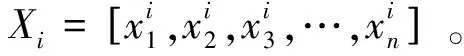
(10)

(1)利用场景距离测算对相似场景进行削减，综合考虑场景间的概率距离，即

(11)

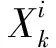
(2)从场景集中剔除距离场景i最近的场景j：

(12)

(3)更新场景i出现的概率：

(13)

(4)重复步骤(1)—(3)，直到场景数量削减至N′。

3)风光机组发电成本模型。

风电机组发电在实际运行中，其发电边际成本可以近似为0，因此风电机组发电成本Cwpp主要由建设成本以及运维成本组成。

(14)

式中：cwpp、Pwpp(t)分别为风电机组的单位功率发电成本和t时刻风电机组的发电功率；ΔT为调度时间跨度，取1 h。

和风电机组类似，光伏机组发电成本Cpv也主要由建设成本以及运维成本组成。

(15)

式中：cpv为光伏机组的单位功率发电成本；Ppv(t)为t时刻光伏机组的发电功率。

2.1.2 储能系统模型构建

由于锂离子电池具有能量密度高、循环寿命周期长、功率密度高、全寿命充放电次数多、放电深度大等优势[28]，本文的储能单元均由锂离子电池组成。储能系统的运行成本Cess由建设成本、运维成本和由充放电造成的电池损耗成本构成。

(16)

式中：cess为储能系统单位功率的运行成本，取0.01元/(kW·h)[29]；Pessc(t)、Pessd(t)分别为t时刻储能系统的充、放电功率；μessc(t)、μessd(t)分别为t时刻储能系统的充、放电控制变量，为0-1变量。

2.1.3 柔性负荷需求响应模型构建

基于事先签订的需求响应合同，由VPP运营商向柔性负荷用户直接发出负荷削减的控制信号，以达到特定的响应目标。

Pu(t)=Puo(t)-Pud(t)

(17)

式中：Pu(t)为t时刻削减后的用户负荷功率；Puo(t)为t时刻削减前的原始用户负荷功率；Pud(t)为t时刻削减的用户负荷功率。

2.2 目标函数

本文以VPP运行收益最大为目标进行决策，其表达式为：

maxF=(Rbm+Rrm)-(Cbm+

Crm+Cwpp+Cpv+Cess)

(18)

式中：Rbm、Rrm分别为VPP向日前市场和实时市场售电的收益；Cbm、Crm分别为VPP从日前市场和实时市场购电的成本。

(19)

(20)

式中：Pbms(t)为t时刻VPP在日前市场上的售电功率；Prms(t)为t时刻VPP在实时市场上的售电功率。

(21)

(22)

式中：Pbmb(t)为t时刻VPP在日前市场上的购电功率；Prmb(t)为t时刻VPP在实时市场上的购电功率。

2.3 约束条件

1)功率平衡约束。

Pwpp(t)+Ppv(t)+Pbmb(t)+Prmb(t)+ηessPessd(t)=

Pu(t)+Pbms(t)+Prms(t)+Pessc(t)

(23)

式中：ηess为储能系统的充放电效率。

2)风电、光伏出力约束。

(24)

(25)

3)储能系统运行约束。

(26)

(27)

(28)

(29)

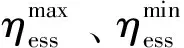
由于储能系统不能同时充、放电，同时运行周期结束时储能蓄电量需恢复到最初状态，即：

0≤μessc(t)+μessd(t)≤1

(30)

Sess(0)=Sess(24)

(31)

4)负荷削减约束。

为保证负荷用户的正常用能，VPP对负荷用户的负荷削减不得大于最大可削减量。

0≤Pud≤εmaxPuo

(32)

式中：εmax为最大负荷削减率。

5)电压约束。

Vmin≤V(t)≤Vmax

(33)

式中：V(t)为t时刻的节点电压；Vmax、Vmin分别为节点电压上下限。

6)馈线容量约束。

(34)

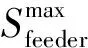
7)主网约束。

(35)

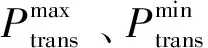
3 基于Owen值法的双层收益分配

3.1 Owen值法

合作联盟形成的关键在于利益分配是否合理和公平[30]。同样地，VPP的稳定运行也需要公平合理的收益分配来予以保证。但由于传统VPP不同参与者之间通常不直接共享储能，现有的常规收益分配方法把每个储能系统都视为独立参与者进行分析，这与本文的共享储能机制实际运行方式相悖，可能会导致分配不合理。因此，本文采用Owen值法来进行含共享储能的VPP收益分配。Owen值法作为Shapley值法的延拓，将收益分配分为2个阶段，第一步是在各优先联盟之间进行收益分配，为每个优先联盟分配一个整体收益；第二步是将优先联盟的整体收益在其内部各参与者之间进行收益分配[31]。

风光机组、共享储能和负荷作为联盟参与者合作形成联盟，即VPP；参与者集合表示为N={WPP,PV,Shared-ESS,Load}，一部分参与者的组合构成子联盟S，排除没有任何参与者的子联盟，该联盟共有24-1个子联盟；其中共享储能构成一个优先联盟，其参与者为风电、光伏和独立投资主体的储能系统，优先联盟参与者集合表示为M={WPP-ESS,PV-ESS,Independent-ESS}。本文的VPP联盟各参与者收益分配问题和共享储能优先联盟收益分配问题均符合Shapley值法的应用背景。综上，本文采用Owen值法将含共享储能的虚拟电厂整体运行收益经过2次Shapley值法分配，下沉到具体的每个参与者，实现利益的合理分配[32]。

3.2 上层虚拟电厂收益分配

对于一个由N个参与者构成的联盟，假设i表示第i个参与者，S表示该联盟中一部分参与者构成的子联盟，n表示子联盟S中参与者的个数，R(S)表示由S构成的联盟取得的总收益，R(S∪i)表示第i个参与者加入后联盟取得的收益，则该联盟中第i个参与者所应分配到的收益v(i)为：

(36)

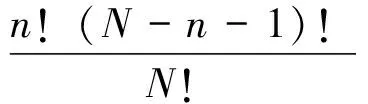
3.3 下层共享储能收益分配

VPP的总收益在根据贡献度相应地分配到每个参与者后，须对共享储能分配到的收益进一步下沉，将其合理地再分配到参与共享储能的每个单元。共享储能的收益采用常规Shapley值法来进行分配，分配方法同3.2节VPP运行收益分配的方法。假设Shared-ESS优先联盟由M个储能单元构成，则第j个储能单元分配到的收益v(j)为：

(37)

3.4 双层收益分配流程

上述基于Owen值法的双层收益分配方法主要包括上层VPP参与者间收益分配和下层共享储能内各储能单元收益分配2个过程，具体分配流程如图5所示。

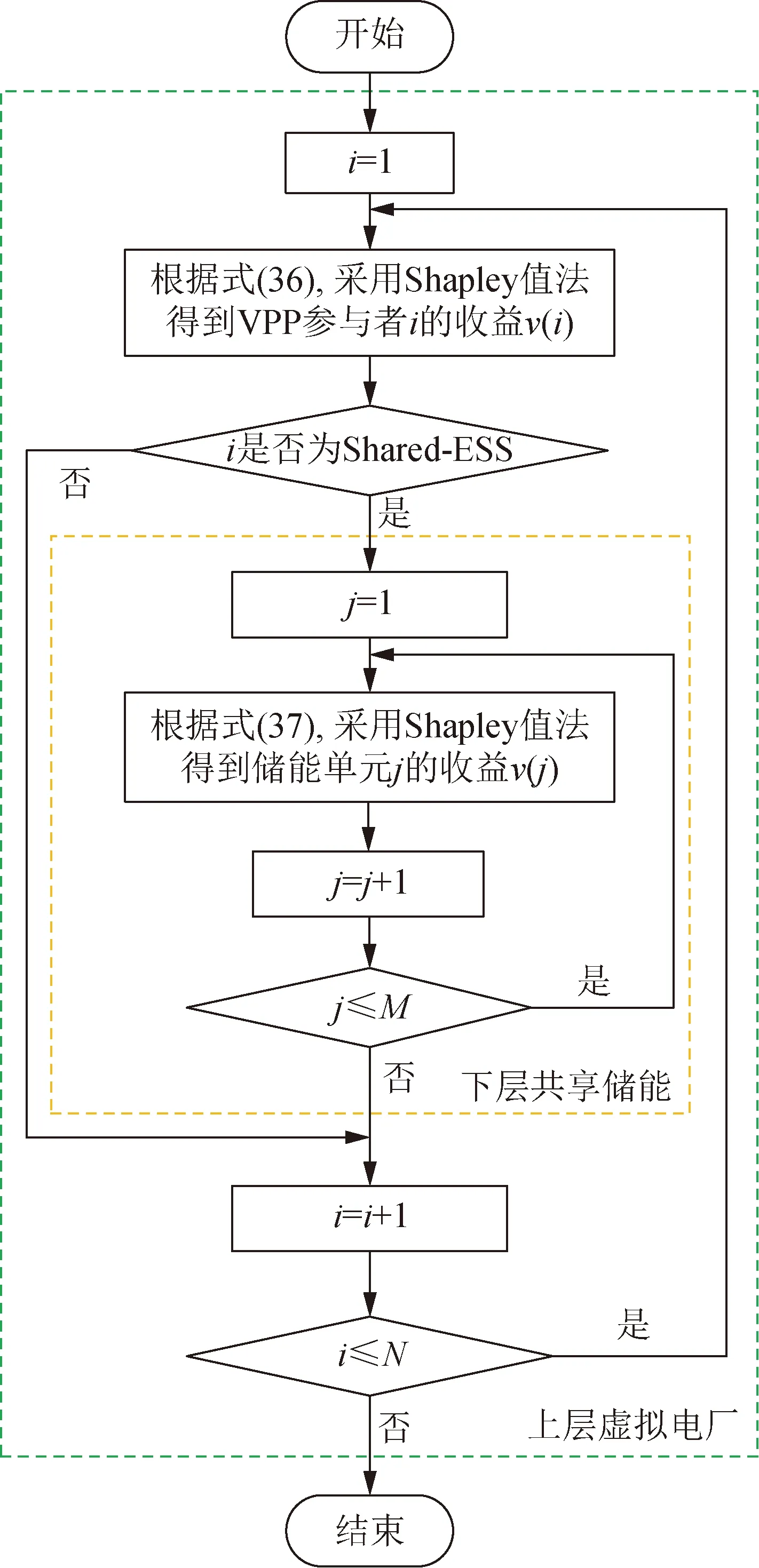
图5 双层收益分配流程

4 算例分析

4.1 参数设置

本文以中国北方某园区为研究对象，VPP的风电、光伏机组装机容量分别为6、3 MW，风电、光伏机组分别配置有容量为2、1 MW·h的储能系统；另外，VPP内还有容量为1 MW·h的独立储能系统和最大削减率εmax=10%的可削减负荷。风电机组、光伏机组和储能系统的详细参数见表1—3。

表1 风电机组参数

表2 光伏机组参数

表3 储能系统参数

本文的VPP参与电网的峰谷分时电价需求响应。峰时(11:00—15：00，18:00—21:00)电价为1 390.8元/(MW·h)，平时(07:00—11:00，15:00—18:00，21:00—23:00)电价为869.25元/(MW·h)，谷时(23:00—07:00)电价为347.7元/(MW·h)。

本文分别削减生成10个风电出力典型场景和10个光伏出力典型场景，各取5个场景数据作为预测出力和实际出力，风光场景削减结果如图6、7所示。风电、光伏出力数据和负荷数据如图8所示。

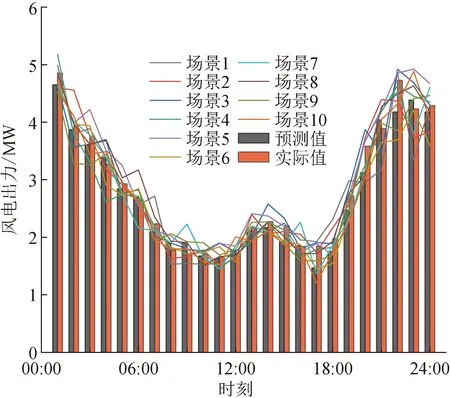
图6 风电场景削减

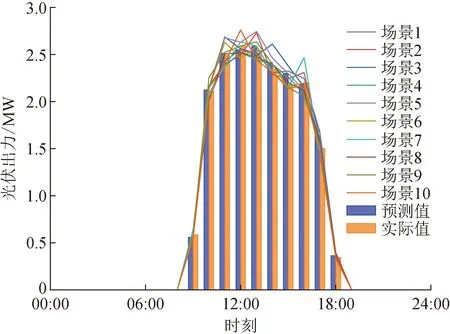
图7 光伏场景削减

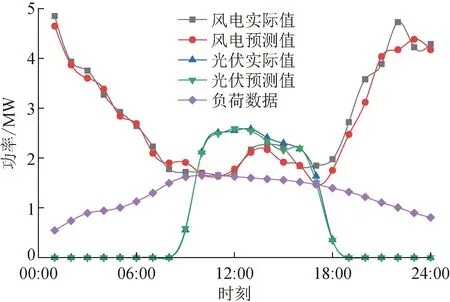
图8 风光出力及负荷数据

在仿真分析中，本文采用MATLAB R2018b软件,通过Yalmip工具包调用Gurobi对算例进行求解，计算机参数为Intel(R)Core(TM)i5 2.30 GHz，8 GB内存。

4.2 情景设置

为了更好地体现本文所构建含共享储能VPP的优势，本文设置了4种情景，以此来展示储能共享前后和用户参与需求响应前后的变化。

情景1：VPP含有风电机组和光伏机组，但不配置储能系统；无独立储能系统；负荷不参与需求响应。

情景2：VPP含有风电机组和光伏机组，分别配置储能系统；VPP同时配置独立储能系统；负荷不参与需求响应。

情景3：VPP含有风电机组和光伏机组，分别配置储能系统；VPP同时配置独立储能系统；所有储能系统参与共享储能；负荷不参与需求响应。

情景4：VPP含有风电机组和光伏机组，分别配置储能系统；VPP同时配置独立储能系统；所有储能系统参与共享储能；负荷参与需求响应。

4.3 算例结果对比分析

4.3.1 VPP运行收益结果对比分析

不同情景下VPP的优化运行收益结果如表4所示。

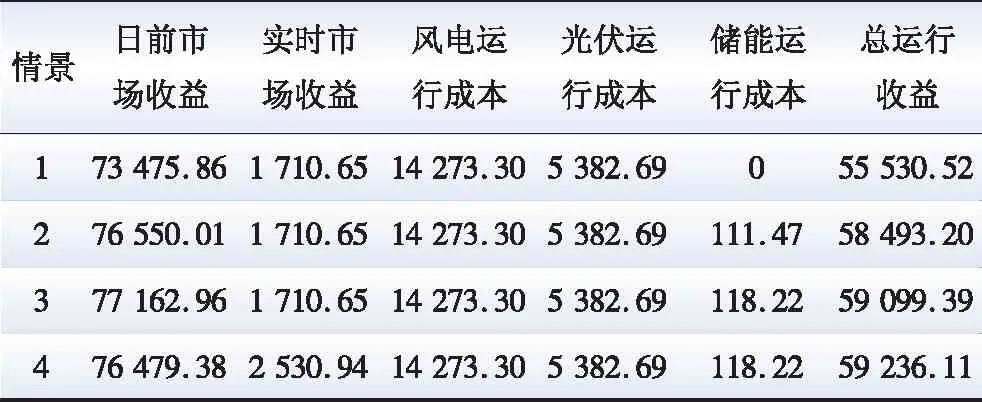
表4 不同情景下VPP的运行收益

由表4可知，情景2相对于情景1，VPP的运行收益增加了2 962.68元，收益增加率为5.34%，这部分增长主要是得益于VPP在日前市场上净收益的增加；情景3相对于情景2，VPP的运行收益增加了606.19元，收益增加率提升了20.46%，这是因为VPP在日前市场上的收益进一步增加了；情景4相对于情景3，VPP的运行收益又增加了136.72元，收益增加率提升了3.83%，这部分的增长主要来自于VPP在两级电力市场上净收益的增加。

上述结果表明了本文所提含共享储能的VPP相对于传统不含共享储能的VPP可以显著提升运行收益，说明了本文模型在经济性上的优越性。

4.3.2 两级电力市场VPP购售电结果对比分析

各情景下的VPP在两级电力市场购售电量结果对比如图9所示。正值表示VPP向电力市场售电，负值表示VPP向电力市场购电。

图9 VPP的购售电量

由图8和图9中的负荷曲线和日前市场购售电量曲线可以得知，在情景1条件下，VPP在日前向电力市场和用户共出售电能84.58 MW·h。由于ESS在充、放电时存在电能损耗，因此在情景2和情景3下，VPP向日前市场出售的电能减少了约1.11 MW·h。由于情景4的负荷参与需求响应和共享储能，VPP在日前市场上向负荷的售电量下降，因此情景4的日前售电量相对于前2个情景，进一步降低约0.84 MW·h。配置了ESS的情景2、情景3和情景4在峰时段(11:00—15:00，18:00—21:00)的售电量均高于无ESS的情景1，这是因为配置ESS的VPP可以通过ESS在电价低谷时段储存风电、光伏的电能，然后在电价高峰时段释放电能，实现峰谷价差套利。因此，情景2、情景3和情景4可以在出售电能总量均小于情景1的情况下，实现日前市场售电收益的增加。

由图9中实时市场购售电量曲线可以得知，各情景在实时市场上的售电量一致，均为3.56 MW·h；情景1、情景2和情景3在实时市场上的购电量为0.94 MW·h，相对于其他情景，情景4的实时市场购电量降低超过79.69%，为0.19 MW·h。这是因为情景4的负荷参与需求响应，平抑了一部分可再生能源出力偏差。因为实时市场失衡电价惩罚系数的存在，在售电量相同的情况下，情景4的购电量较少，因此其在两级电力市场的净收益相对于其他情景至少增加136.72元。

4.3.3 储能系统优化结果对比分析

ESS蓄电量及充、放电功率如图10所示。ESS和共享ESS蓄电率对比如图11所示。由图10可知，采用了本文所提共享ESS的情景3和情景4，ESS的充、放电总功率高于不采用共享ESS的情景2，ESS利用率比情景2提升了6个百分点。结合表4可以看出，因为充、放电总功率的增加，情景3的储能运行成本相对于情景2增加了6.76元，但是其在日前市场上的收益显著增加了612.95元。这是因为共享ESS可以实现不同可再生能源之间的能量交换，提高ESS储能单元的利用率，从而可以更好地利用峰谷价差来进行“低储高放”套利，进而有效增加VPP的运行收益。

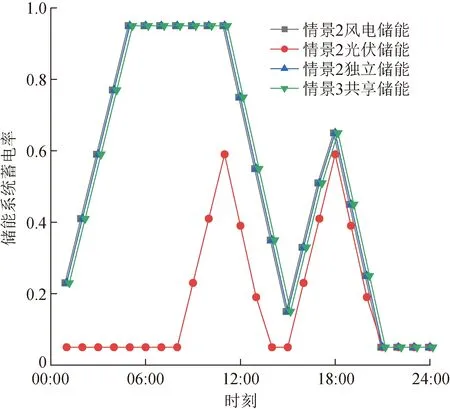
图11 ESS和共享ESS蓄电率对比

结合图11和图8中的光伏机组出力数据可以得知，光伏机组在08:00才开始发电，因此在峰时段11:00到来前，ESS只有3 h进行充电操作，由于ESS最大充电速率的限制，光伏ESS无法在峰时段到来前达到最大蓄电量，进而导致情景2的光伏ESS的蓄电率低于全天24 h均有发电的风电ESS。结合图10可以得知，情景2中ESS平均蓄电量较低的原因是光伏ESS的利用率相对不足。由图11可以进一步得出，情景3的共享ESS的蓄电率整体高于情景2的光伏ESS，其全天平均蓄电率为0.535，相对于情景2的光伏ESS显著提升了19.95%。这说明在参与共享储能的情况下，可以有效提高ESS的利用率，进而增加VPP的运行收益。

需求响应前后失衡电量对比如图12所示。由图12可知，情景4中柔性负荷参与了需求响应，通过负荷削减平抑了风电、光伏预测出力和实际出力的偏差，相对于其他情景，情景4的失衡电量降低了16.61%。结合情景4的优化结果可知，VPP都在失衡电量为负的时点进行负荷削减调度，使得VPP在实时市场上为消除失衡电量的购电成本降低，因此在实时市场售电收益一致的情况下，相对于其他情景，情景4在实时市场上的净收益增幅可观，约为47.95%。结合图8的负荷数据可以得出，在最优场景下，柔性负荷的各时段负荷削减率均不大于10%，且平均负荷削减率为2.49%，远小于最大负荷削减率。这说明本文构建的柔性负荷模型在很好地保证负荷用户用电稳定性的同时，还可以进行适当的负荷需求响应，提升VPP的灵活性和运行收益。

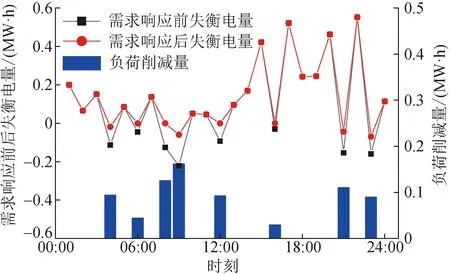
图12 需求响应前后失衡电量对比

4.4 敏感性分析

本文基于情景4对4项因素进行了敏感性分析。首先研究了ESS相关参数对VPP运行收益的影响，即不同的ESS容量和充电速率导致VPP运行收益的变化；同时，本文还分析了最大负荷削减率和电价对VPP运行收益的影响。ESS相关参数对VPP运行收益的影响如图13所示。

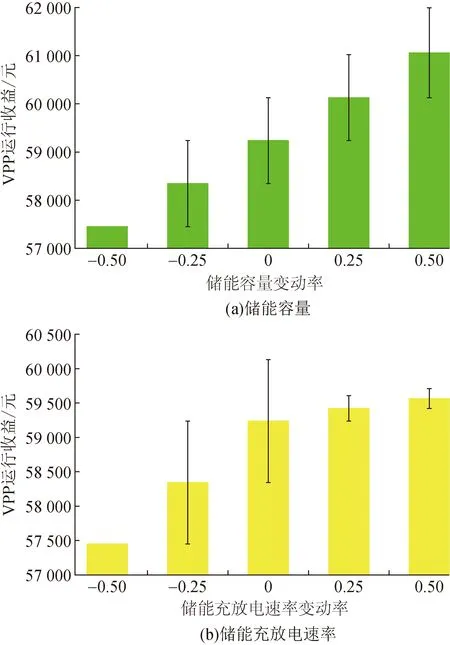
图13 ESS相关参数对VPP运行收益的影响

为了分析ESS容量这一单一因素的影响，假设其他因素不变，即ESS单元的最大充、放电速率为0.2 MW/h，最大负荷削减率为10%，电价不变。其结果如图13(a)所示，横坐标0表示ESS的默认容量，即4 MW·h，-0.50表示容量减少50%即2 MW·h。由图可知，ESS容量变动率在(-0.50，0.50)区间内，ESS容量和VPP运行收益呈正相关，但在ESS容量增加50%时，VPP运行收益的增加有所降低，这是因为在17:00—18:00风光出力较低，为优先满足负荷电能供给，以致ESS的充电功率低于最大充电功率，因此在下一个峰时段，VPP通过ESS“低储高放”的收益增幅降低。

与ESS容量的敏感性分析一样，为了控制变量，在分析ESS最大充、放电速率的影响时，本文假设ESS容量为4 MW·h，最大负荷削减率和电价同上。其结果如图13(b)所示，横坐标0表示ESS单元的默认最大充、放电速率，即0.2 MW/h，-0.50表示最大充、放电速率为0.1 MW/h。由图可知，储能充放电速率变动率在(-0.50，0.50)的区间内，即随着最大充、放电速率的增加，VPP运行收益也在增加，但是在最大充放电速率增加25%和50%情况下，VPP运行收益增幅逐渐下降，这是由于ESS容量有限，ESS利用率达到一定水平后将不再增加，因此VPP通过“峰谷价差”套利的空间有限。

由上述分析可知，ESS相关参数与VPP运行收益并非线性关系，参数的持续提升并不能获得相应的运行收益增加，综合考虑ESS高昂的配置成本，VPP的ESS要根据其内部可再生能源的发电功率和ESS自身的全寿命周期成本进行优化配置。最大负荷削减率和电价对VPP运行收益的影响如图14所示。

图14 最大负荷削减率和电价对VPP运行收益的影响

本文在分析最大负荷削减率这一敏感性因素时，假设ESS的相关参数和电价保持不变。其结果如图14(a)所示，横坐标0表示柔性负荷的默认最大削减率，即10%，-0.50表示最大负荷削减率为5%。由图可知，最大负荷削减率变动率在(-0.50，0.50)的区间内，即随着最大负荷削减率的增加，VPP运行收益也在增加，但是实际上的收益增加量十分有限，收益增加率在0.01%～0.08%之间。考虑到过度负荷削减会影响到负荷用户的用电稳定性和参与需求响应的积极性，因此合适的负荷削减率对于VPP的运行优化十分重要。

对于电价的敏感性分析结果，如图14(b)所示。分析时同样假设ESS的相关参数和最大负荷削减率不变，且0表示默认的电价，-0.50表示各时段的电价均为默认电价的一半。由图可知，在敏感性分析变化区间内，电价和VPP运行收益呈线性关系，且敏感度较高，电价每变动25%，VPP的运行收益将变化19 752.6元。

由上述分析可知，电价这一敏感因素引起的VPP运行收益变化比其他影响因子至少高出一个数量级，这说明电价是影响VPP运行收益的主要因素，但是VPP作为电力市场的价格接受者，对于电价没有议价权，因此ESS相关参数对VPP运行收益的影响就显得十分重要，在考虑ESS初期投资成本的情况下，可适当优化ESS相关参数以获得VPP运行收益的增加。

4.5 收益分配结果分析

本文将风光机组、共享储能系统和柔性负荷进行联盟组合并编号，1表示该机组参与VPP联盟，反之，0表示不参与。本文假设共享储能和柔性负荷不单独参与电力市场交易，因此不存在共享储能或柔性负荷单独存在的联盟组合，也不存在两者合作的联盟组合。VPP的各种联盟组合运行收益如表5所示。

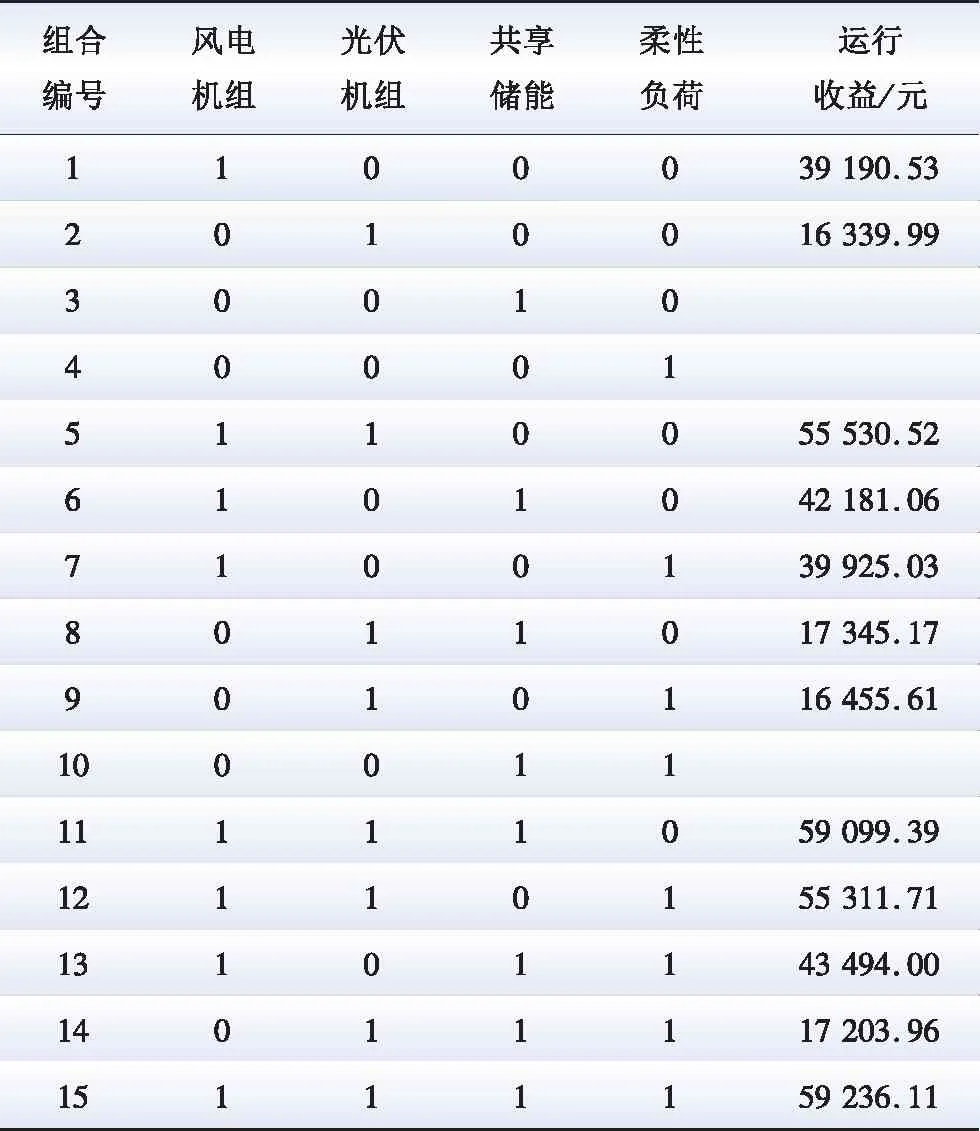
表5 VPP联盟组合运行收益

4.5.1 VPP收益分配结果

根据本文所提出的Owen值法，结合各联盟组合运行收益数据对VPP各参与者进行收益分配，其结果如表6所示。

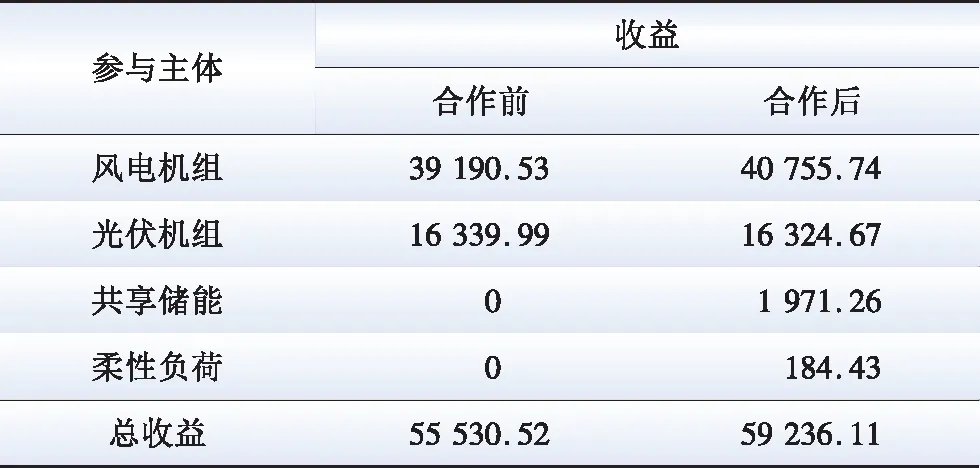
表6 VPP收益分配结果

由表6可以看出，VPP合作后的运行收益相较于合作前增加了3 705.59元，且各参与者分配到的收益均得到了提升。其中，共享储能的收益增加得最多，为1 971.26元，超过总收益增加的一半，究其原因，共享储能系统可以在电价低谷期消纳风光多余出力，再在电价高峰期放电套利，是整个VPP运行收益增加最主要的贡献者，故在收益分配时应分得最多的增量收益。

4.5.2 共享储能收益分配结果

基于上述仿真结果，根据Owen值法第二阶段的收益分配法，对ESS在VPP层面分得的收益进行第二次分配，其结果如表7所示。

表7 共享ESS收益分配结果

由表7可以得出，共享ESS各单元获得的收益和其容量相关，即风电储能的容量是光伏储能和独立储能的2倍，其通过分配得到的收益也是后两者的2倍。究其原因，结合4.4节的敏感性分析可知，在本文的仿真环境下，不同的ESS单元的下层联盟组合的容量均在敏感性曲线的线性区间内，故单位ESS容量分配到的收益也是一定的。

5 结 论

本文构建了日前-实时市场环境下含共享储能的虚拟电厂运行优化模型，并基于Owen值法，对上层VPP运行收益和下层共享储能收益进行了合理分配，算例结果表明：

1)共享储能模式可以有效整合分属不同主体的储能资源，发挥共享储能的规模效应，有效平抑风光出力偏差，提高VPP运行的经济性。

2)Owen值法可以很好地完成对具有优先联盟的VPP运行收益的分配及共享储能内部的收益分配，说明其具有相当适配性和实际应用价值。

3)本文所作的敏感分析得出，电价是影响VPP运行收益最主要的因素，另外通过适当提升ESS相关参数也可以提升VPP运行收益，这为含储能的VPP降本增效指明了方向。

值得注意的是，本文的优化过程暂未考虑用户负荷波动等不确定性因素，并且只考虑了24时点的电力市场交易机制。因此，负荷不确定性和精细尺度下的电力市场交易机制将是后续工作的重点。